University of Manchester School of Computer Science Comp

University of Manchester School of Computer Science Comp 30291 : Digital Media Processing Section 5 z-transforms & IIR-type digital filters 24 Nov'09 Comp 30291 DMP Section 5 1

Introduction • General causal digital filter has difference equation: • Order is maximum of N and M. • Recursive if any b j is non-zero. • A 2 nd order recursive filter has the difference-equation: y[n] = a 0 x[n] + a 1 x[n-1] + a 2 x[n-2] - b 1 y[n-1] - b 2 y[n-2] 24 Nov'09 Comp 30291 DMP Section 5 2

Signal-flow-graph for 2 nd order recursive diff equn x[n] z-1 a 0 a 1 + y[n] + z-1 + + -b 1 z-1 a 2 -b 2 y[n] = a 0 x[n] + a 1 x[n-1] + a 2 x[n-2] - b 1 y[n-1] - b 2 y[n-2] 24 Nov'09 Comp 30291 DMP Section 5 3

Derivation of ‘z-transform’ If {x[n]} with x[n] = zn is applied to an LTI system with impulseresponse {h[n]}, output would be, by convolution : 24 Nov'09 Comp 30291 DMP Section 5 4

‘z-transform’ of {h[n]} • If input is {zn}, output is {H(z). zn} • z may be any real or complex number for which series converges. • For causal & stable IIR, the series converges when |z| 1. • Replacing z by ej gives frequency-response: 24 Nov'09 Comp 30291 DMP Section 5 5

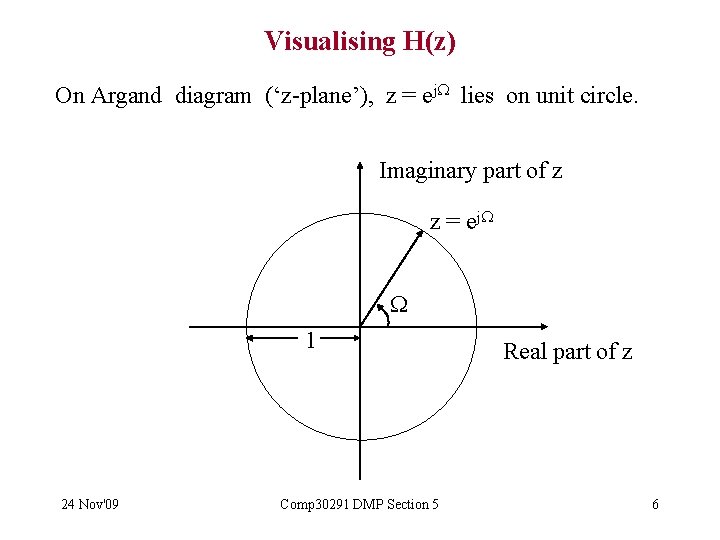
Visualising H(z) On Argand diagram (‘z-plane’), z = ej lies on unit circle. Imaginary part of z z = ej 1 24 Nov'09 Comp 30291 DMP Section 5 Real part of z 6

Example 5. 1 Find H(z) for the non-recursive difference equation: y[n] = x[n] + x[n-1] Solution: {h[n]} = {. . . , 0, 1, 1, 0, . . . }, therefore H(z) = 1 + z - 1 24 Nov'09 Comp 30291 DMP Section 5 7

Example 5. 2 • Find H(z) for the recursive difference equation: y[n] = a 0 x[n] + a 1 x[n-1] - b 1 y[n-1] Solution: If x[n] = z n then y[n] = H(z) z n , y[n-1] = H(z) z n - 1 • Substitute to obtain: H(z) z n H(z) = a 0 z n + a 1 z n - 1 - b 1 H(z) z n - 1 = a 0 + a 1 z - 1 - b 1 H(z) z - 1 (1 + b 1 z-1) H(z) = a 0 + a 1 z-1 • When z = -b 1, H(z) = 24 Nov'09 Comp 30291 DMP Section 5 8

Find H(z) for the 2 nd order difference-equation y[n] = a 0 x[n] + a 1 x[n-1] + a 2 x[n-2] - b 1 y[n-1] - b 2 y[n-2] The same method gives: H(z) z n = a 0 zn + a 1 zn - 1 +a 2 zn - 2 - b 1 H(z) zn - 1 - b 2 H(z)zn-2 a 0 + a 1 z-1 + a 2 z-2 H(z) = b 0 + b 1 z-1 + b 2 z-2 24 Nov'09 Comp 30291 DMP Section 5 with b 0 = 1. 9

Consider difference-equation for general digital filter y[n] = i=0 N M a i x[n i] b j y[n j] j=1 • The same method gives: • This is the ‘system function’ of the digital filter. • Also referred to as ‘transfer function’ 24 Nov'09 Comp 30291 DMP Section 5 10

System function • Ratio of 2 polynomials in z-1 • Equal to z-transform of impulse-response when this converges. • Easily derived from difference-equation & signal-flow graph. • Replacing z by ej gives frequency-response 24 Nov'09 Comp 30291 DMP Section 5 11

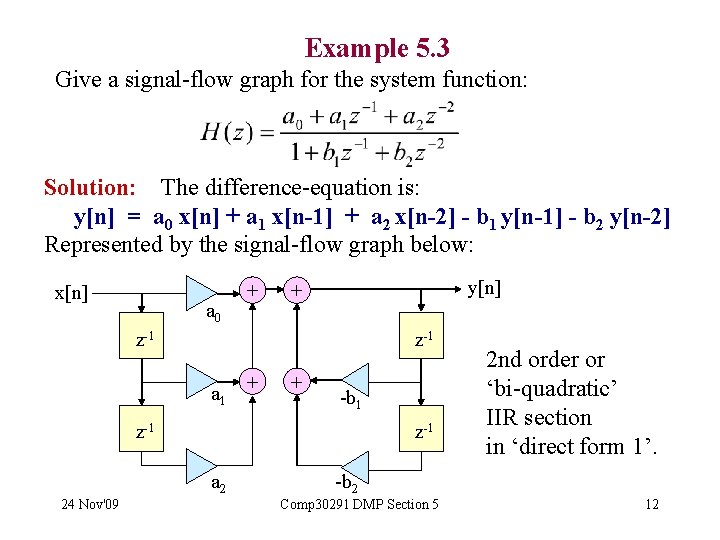
Example 5. 3 Give a signal-flow graph for the system function: Solution: The difference-equation is: y[n] = a 0 x[n] + a 1 x[n-1] + a 2 x[n-2] - b 1 y[n-1] - b 2 y[n-2] Represented by the signal-flow graph below: x[n] a 0 + y[n] + z-1 a 1 + + -b 1 z-1 a 2 24 Nov'09 2 nd order or ‘bi-quadratic’ IIR section in ‘direct form 1’. -b 2 Comp 30291 DMP Section 5 12

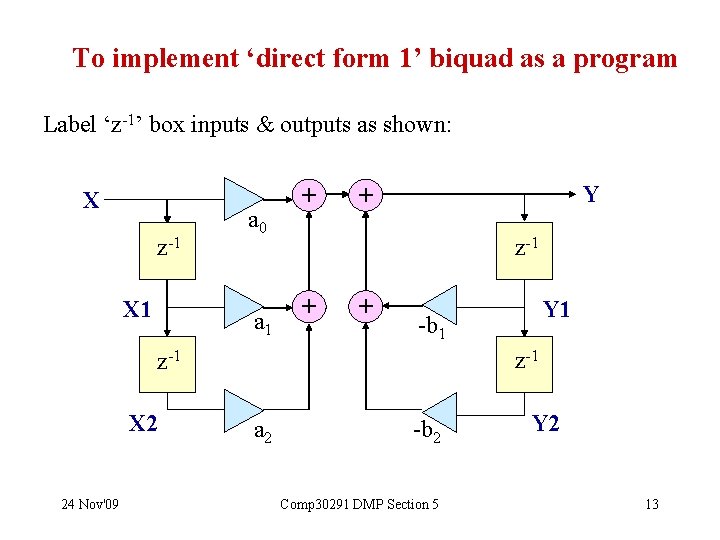
To implement ‘direct form 1’ biquad as a program Label ‘z-1’ box inputs & outputs as shown: X z-1 X 1 a 0 a 1 + Y + z-1 + + -b 1 z-1 X 2 24 Nov'09 Y 1 a 2 -b 2 Comp 30291 DMP Section 5 Y 2 13

In MATLAB using floating point arithmetic X 1=0; X 2=0; Y 1=0; Y 2=0; while 1 X = input(‘X=’); Y = a 0*X + a 1*X 1 + a 2*X 2 - b 1*Y 1 - b 2*Y 2; disp(sprintf(‘Y = %f’ , Y) ) ; % output Y X 2 = X 1; X 1 = X ; Y 2 = Y 1; Y 1 = Y ; end; 24 Nov'09 Comp 30291 DMP Section 5 14

In MATLAB using Signal Processing toolbox: y = filter([a 0 a 1 a 2], [b 0 b 1 b 2], x ); 24 Nov'09 Comp 30291 DMP Section 5 15

In MATLAB using fixed point arith & shifting K=1024; A 0=round(a 0*K); A 1=round(a 1*K); A 2=round(a 2*K); B 1=round(b 1*K); B 2=round(b 2*K); X 1=0; X 2=0; Y 1=0; Y 2=0; while 1 X = input(‘X=’) ; Y = A 0*X + A 1*X 1 + A 2*X 2 - A 1*Y 1 - A 2*Y 2 ; Y = round(Y/K); % Divide by arith right shift disp(sprint(‘Y=%f’, Y)); % Output Y X 2 = X 1; X 1 = X ; % Prepare for next time Y 2 = Y 1; Y 1 = Y ; end; 24 Nov'09 Comp 30291 DMP Section 5 16

Look again at ‘Direct Form 1’ signal-flow-graph x[n] a 0 + y[n] + z-1 a 1 + + -b 1 z-1 a 2 -b 2 • It may be thought of as two signal-flow-graphs: x[n] 24 Nov'09 Non-recursive part Recursive part Comp 30291 DMP Section 5 y[n] 17

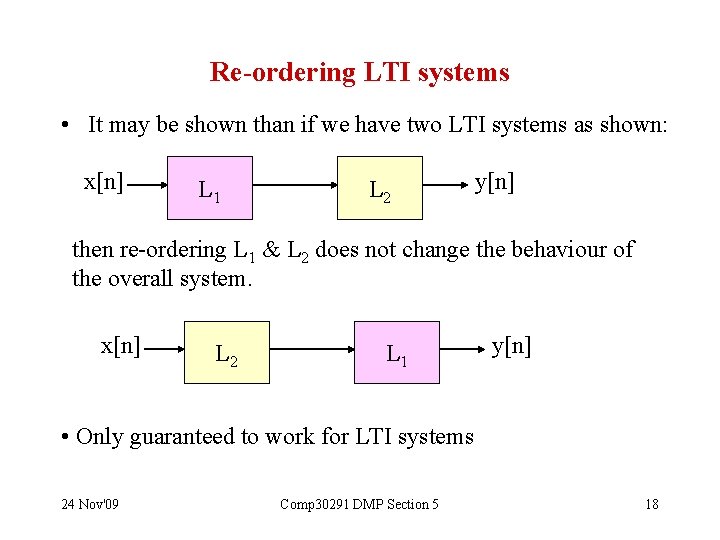
Re-ordering LTI systems • It may be shown than if we have two LTI systems as shown: x[n] L 1 L 2 y[n] then re-ordering L 1 & L 2 does not change the behaviour of the overall system. x[n] L 2 L 1 y[n] • Only guaranteed to work for LTI systems 24 Nov'09 Comp 30291 DMP Section 5 18

Alternative signal-flow-graph Look again at ‘Direct Form 1’: x[n] + a 0 y[n] + z-1 a 1 + + -b 1 z-1 a 2 -b 2 Re-order the two ‘halves’ & then simplify to ‘direct form 2’: x[n] + z-1 a 1 -b 1 z-1 -b 2 24 Nov'09 a 0 + y[n] x[n] + z-1 + + -b 1 z-1 a 0 a 1 + y[n] + z-1 a 2 -b 2 Comp 30291 DMP Section 5 a 2 19

‘Direct Form II’ signal-flow-graph x[n] W + a 0 + y[n] z-1 + W 1 -b 1 a 1 + z-1 -b 2 W 2 • Direct form II economises on ‘delay boxes’. • Notice labels: W, W 1 & W 2 a 2 It is a 2 nd order (bi-quad) section whose system function is: Its difference equation is: y[n] = a 0 x[n] + a 1 x[n-1] + a 2 x[n-2] - b 1 y[n-1] - b 2 y[n-2] i. e. exactly the same as Direct Form 1 24 Nov'09 Comp 30291 DMP Section 5 20

Program to implement Direct Form II using normal arithmetic W 1 = 0; W 2 = 0; %For delay boxes while 1 X = input(‘X=’) ; % Input to X W =X - b 1*W 1 - b 2*W 2; % Recursive part Y = W*a 0 + W 1*a 1 + W 2*a 2; % Non-rec. part W 2 = W 1; W 1 = W; % For next time disp(sprintf(‘Y=%f’, Y)); % Output Y using disp end; % Back for next sample 24 Nov'09 Comp 30291 DMP Section 5 21

Direct Form II in fixed point arithmetic with shifting K=1024; A 0=round(a 0*K); A 1=round(a 1*K); A 2=round(a 2*K); B 1=round(b 1*K); B 2=round(b 2*K); W 1 = 0; W 2 = 0; %For delay boxes while 1 X = input(‘X=’) ; % Assign X to input W =K*X - B 1*W 1 - B 2*W 2; % Recursive part W =round( W / K); % By arith right-shift Y = W*A 0+W 1*A 1+W 2*A 2; % Non-rec. part W 2 = W 1; W 1 = W; %For next time Y = round(Y/K); %By arith right-shift disp(sprintf( ‘Y=%f’, Y)); %Output Y using disp end; % Back for next sample 24 Nov'09 Comp 30291 DMP Section 5 22

Poles & zeros of H(z) • For a discrete time filter: • Re-express as: • Now factorise numerator & denominator: 24 Nov'09 Comp 30291 DMP Section 5 23

Poles & zeros of H(z) continued • z 1 , z 2 , . . . , z N , are ‘zeros’. p 1 , p 2 , . . . , p N , are ‘poles’. • H(z) generally infinite with z equal to a pole. • H(z) generally zero with z equal to a zero. • For a causal stable system all poles must satisfy p i < 1. i. e. on Argand diagram: poles must lie inside unit circle. • No restriction on the positions of zeros. 24 Nov'09 Comp 30291 DMP Section 5 24

Design of IIR ‘notch’ filter • Design a 4 th order 'notch' filter to eliminate an unwanted sinusoid at 800 Hz without severely affecting rest of signal. The sampling rate is FS = 10 k. Hz. • One way is to use the MATLAB function ‘butter’ as follows: FL = 800 – 25 ; FU = 800+25; [a b] = butter(2, [FL FU]/(FS/2), ’stop’); a = [0. 98 -3. 43 4. 96 -3. 43 0. 98] b= [ 1 -3. 47 4. 96 -3. 39 0. 96] freqz(a, b); freqz(a, b, 512, FS); % Better graph axis([0 FS/2 -50 5]); % Scales axes MATLAB response • Notch has -3 d. B frequency band: 25 + 25 = 50 Hz. 24 Nov'09 Comp 30291 DMP Section 5 25

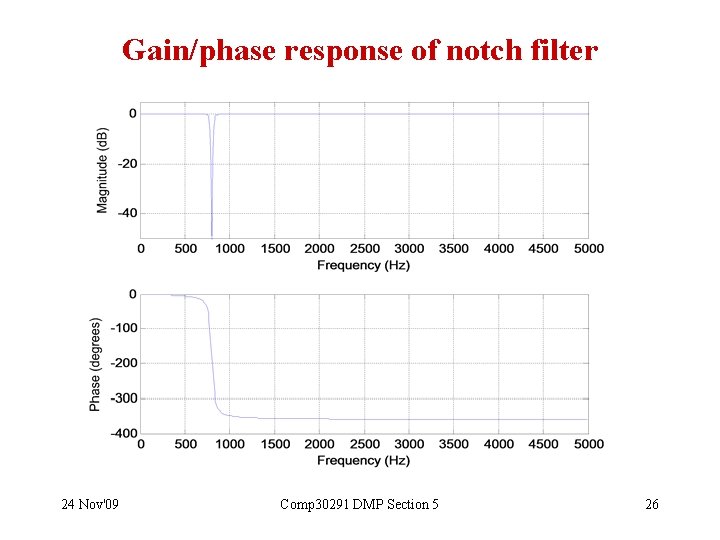
Gain/phase response of notch filter 24 Nov'09 Comp 30291 DMP Section 5 26

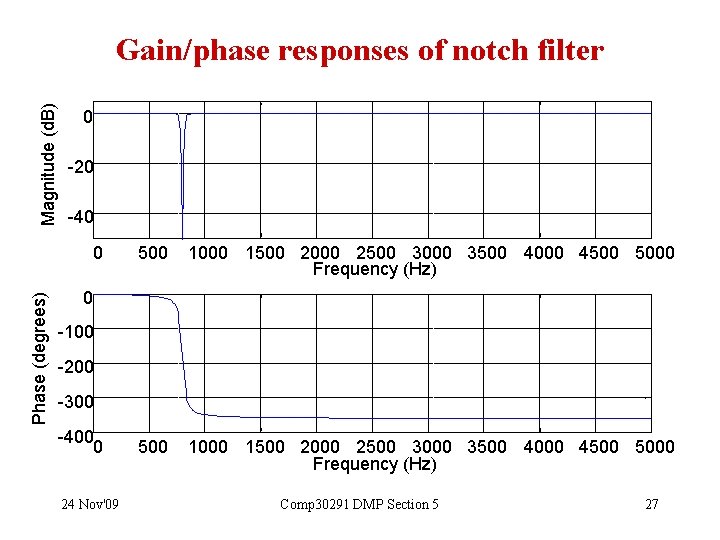
Magnitude (d. B) Gain/phase responses of notch filter 0 -20 -40 Phase (degrees) 0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000 Frequency (Hz) 0 -100 -200 -300 -400 0 24 Nov'09 Comp 30291 DMP Section 5 27

Details • How sharp is the notch? • Can answer this question by specifying notch’s -3 d. B bandwidth. • Have just designed what Barry calls a 4 th order band-stop filter. • MATLAB calls it a 2 nd order band-stop filter. • For a sharper notch, decrease -3 d. B bandwidth • But this will decrease its ‘depth’, i. e. the attenuation at the ‘notch’ frequency. • If necessary, increase the order to 6 (3) or 8 (4). 24 Nov'09 Comp 30291 DMP Section 5 28

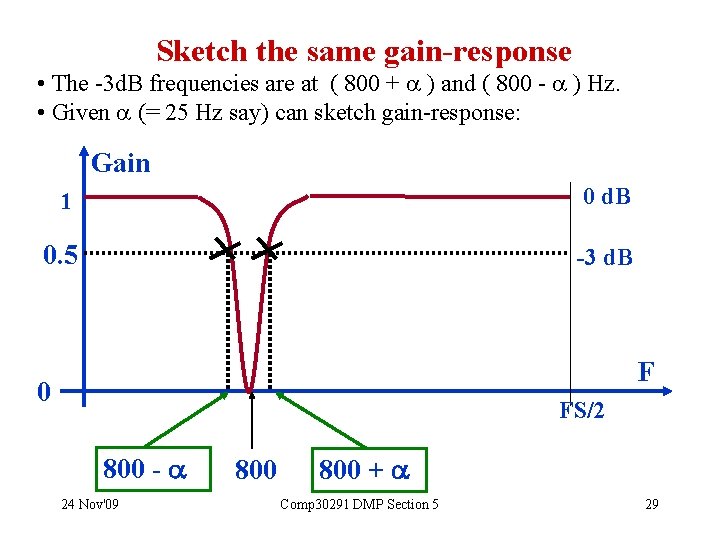
Sketch the same gain-response • The -3 d. B frequencies are at ( 800 + ) and ( 800 - ) Hz. • Given (= 25 Hz say) can sketch gain-response: Gain 1 0 d. B 0. 5 -3 d. B F 0 FS/2 800 - 24 Nov'09 800 + Comp 30291 DMP Section 5 29

Implement the 4 th order ‘notch’ filter MATLAB function gave us: a = [0. 98 -3. 43 4. 96 -3. 43 0. 98] b= [ 1 -3. 47 4. 96 -3. 39 0. 96] Transfer (System) Function is: 24 Nov'09 Comp 30291 DMP Section 5 30

A direct Form 2 implementation of the 4 th order IIR notch filter x[n] + + z-1 3. 47 -4. 96 z-1 + + 3. 39 -0. 96 z-1 0. 98 -3. 43 4. 96 -3. 43 + y[n] + + + 0. 0. 98 24 Nov'09 Comp 30291 DMP Section 5 31

Problems with ‘direct form’ IIR implementations • Implementation on previous slide works fine in MATLAB. • But ‘direct form’ IIR implementations of order >2 are rarely used. • Sensitivity to round-off error in coeff values will be high. • Also range of ‘intermediate’ signals in z-1 boxes is high. • High wordlength floating point arithmetic hides this problem • But in fixed point arithmetic, great difficulty occurs. • Instead we use ‘cascaded biquad sections’ 24 Nov'09 Comp 30291 DMP Section 5 32

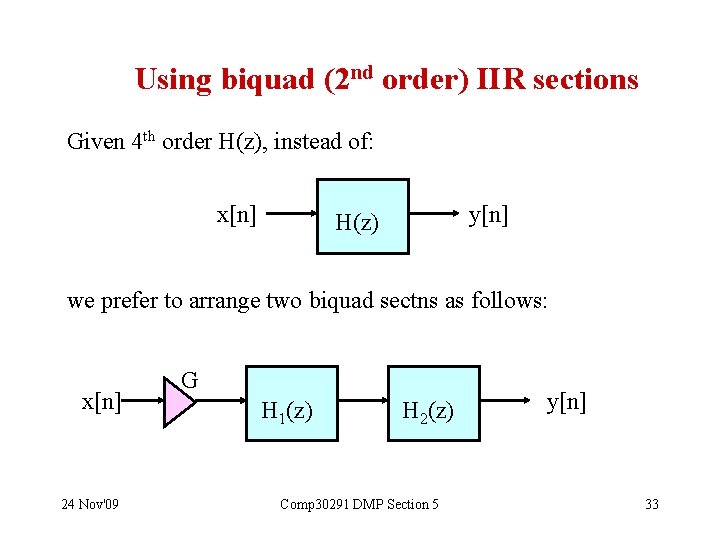
Using biquad (2 nd order) IIR sections Given 4 th order H(z), instead of: x[n] y[n] H(z) we prefer to arrange two biquad sectns as follows: x[n] 24 Nov'09 G H 1(z) H 2(z) Comp 30291 DMP Section 5 y[n] 33

Converting to the new implementation • Get a & b for 4 th order H(z) as before: [a b] = butter(2, [FL FU]/(FS/2), ’stop’); • Then execute: Transfer function [SOS G] = tf 2 sos(a, b) to 2 nd order sectns • MATLAB responds with: First sectn SOS = 1 -1. 753 1 1 -1. 722 0. 9776 nd sectn 2 1 -1. 753 1 1 -1. 744 0. 9785 G = 0. 978 24 Nov'09 Comp 30291 DMP Section 5 34

H(z) may now be realised as: x[n] y[n] 0. 978 1. 722 -0. 978 -1. 753 1. 744 -1. 753 -0. 979 Fourth order IIR notch filter realised as two biquad (SOS) sections 24 Nov'09 Comp 30291 DMP Section 5 35

Example A digital filter with a sampling rate of 200 Hz is required to eliminate an unwanted 50 Hz sinusoidal component of an input signal without affecting the magnitudes of other components too severely. Design a 4 th order "notch" filter for this purpose whose 3 d. B bandwidth is not greater than 3. 2 Hz. Solution method: FS=200; FL=50 -1. 6; FU=50+1. 6; [a b]=butter(2, [FL, FU]/(FS/2), ‘stop’); [SOS G] = tf 2 sos(a, b) 24 Nov'09 Comp 30291 DMP Section 5 36

IIR digital filter design by bilinear transformation • Many design techniques for IIR digital filters have adopted ideas of analogue filters. • Can transform analogue ‘prototype’ transfer function Ha(s) into H(z) for an IIR digital filter. • Analogue filters have infinite impulse-responses. • Many gain-response approximations exist which are realisable by analogue filters • e. g. Butterworth low-pass approximation which can be transformed to high-pass, band-pass & band-stop. 24 Nov'09 Comp 30291 DMP Section 5 37

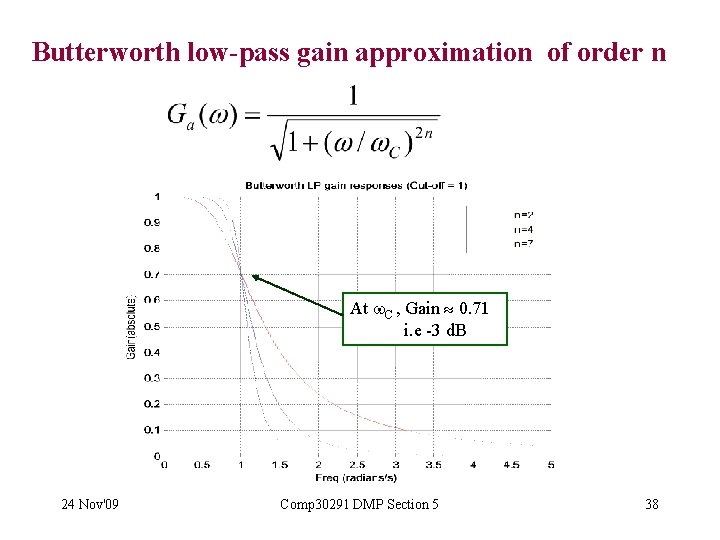
Butterworth low-pass gain approximation of order n At C , Gain 0. 71 i. e -3 d. B 24 Nov'09 Comp 30291 DMP Section 5 38

Transformations from Ha(s) to H(z) for IIR digital filter • Can transform Ha(s), with gain-response Ga( ), to H(z) for an IIR digital filter with similar gain-response G( ). • Many ways exist. • Most famous is ‘bilinear transformation’. • Replaces s by 2(z-1)/(z+1) to transform Ha(s) to H(z). • Fortunately MATLAB does all this for us. 24 Nov'09 Comp 30291 DMP Section 5 39

Properties of bilinear transformation (i) Order of H(z) = order of Ha(s) (ii) If Ha(s) is causal & stable, so is H(z). (iii) G( ) = Ga( ) where = 2 tan( /2) So gain of analog filter at radians/second becomes gain of digital filter at radians/sample where = 2 tan( /2). 24 Nov'09 Comp 30291 DMP Section 5 40

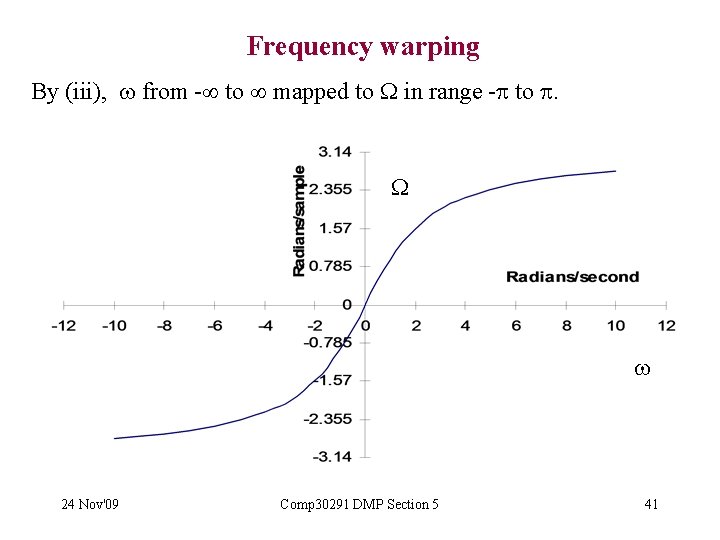
Frequency warping By (iii), from - to mapped to in range - to . 24 Nov'09 Comp 30291 DMP Section 5 41

Frequency warping (cont) • Shape of G( ) will change under the transformation. • If Ga( ) is Butterworth, G( ) will not have exactly the same shape, but we still call it Butterworth. • Mapping approx linear for in the range -2 to 2. • As increases above 2 , a given increase in produces smaller and smaller increases in . 24 Nov'09 Comp 30291 DMP Section 5 42

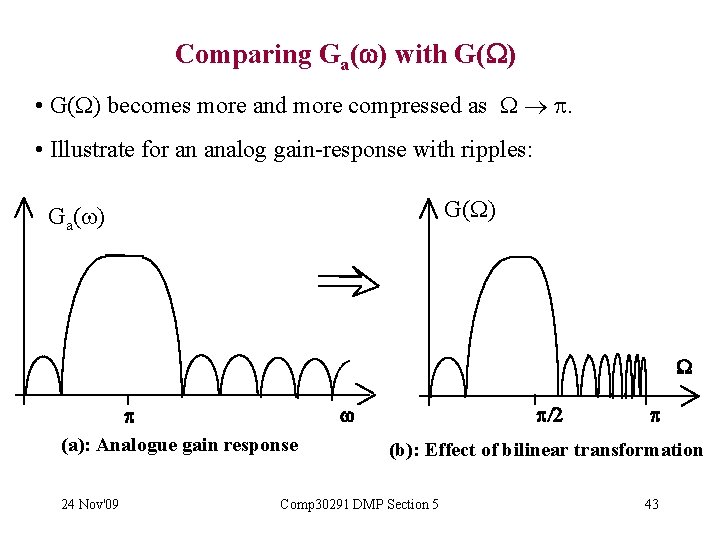
Comparing Ga( ) with G( ) • G( ) becomes more and more compressed as . • Illustrate for an analog gain-response with ripples: G( ) Ga( ) p (a): Analogue gain response 24 Nov'09 p/2 p (b): Effect of bilinear transformation Comp 30291 DMP Section 5 43

‘Prototype’ analogue transfer function • Although the shape changes, we would like G( ) at its cut off C to the same as Ga( ) at its cut-off frequency. • If Ga( ) is Butterworth, it is -3 d. B at its cut-off freq • So we would like G( ) to be -3 d. B at its cut-off C. • Achieved if analogue prototype is designed to have its cutoff frequency at C = 2 tan( C/2). • C is the ‘pre-warped’ cut-off frequency. • Designing analog prototype with cut-off freq 2 tan( C/2) guarantees that the digital filter will have its cut-off at C. 24 Nov'09 Comp 30291 DMP Section 5 44

Design 2 nd order IIR lowpass digital filter by bilinear transfm • Let required cut-off frequency C = /4 radians/sample. • Need prototype transfer fn Ha(s) for 2 nd order Butt low-pass filter with 3 d. B cut-off at 2 tan( C/2) = 2 tan( /8) radians/second. • C = 2 tan( /8) = 0. 828 • I happen to remember that the transfer fn for a 2 nd order Butt lowpass filter with cut-off C is: • If you don’t believe me, check that replacing s by j and taking the modulus gives G( ) = 1/ [1+( / C)2 n] with n=2. • Set C = 0. 828 in this formula, then replace s by 2(z-1)/(z+1). • Gives us H(z) for an IIR digital filter. That’s it! 24 Nov'09 Comp 30291 DMP Section 5 45

Resulting IIR digital filter x[n] y[n] 0. 098 0. 94 2 -0. 33 - 24 Nov'09 Comp 30291 DMP Section 5 46

Design of 2 nd order IIR low-pass digital filter by bilinear transform using MATLAB • If required cut-off freq is /4 radians/sample, type: [a b] = butter(2, 0. 25) • MATLAB gives us: a = [0. 098 0. 196 0. 098] b = [1 -0. 94 0. 33] The required expression for H(z) is therefore: To save multipliers it is a good idea to re-express this as: 24 Nov'09 Comp 30291 DMP Section 5 47

Realise by ‘direct form 2’ signal-flow graph x[n] y[n] 0. 098 0. 94 2 -0. 33 24 Nov'09 Comp 30291 DMP Section 5 48

Higher order IIR digital filters Example: Design 4 th order Butterwth-type IIR low-pass digital filter with 3 d. B c/o at f. S / 16. . Solution: Relative cut-off frequency is /8. Typing: [a b] = butter(4, 0. 125) gives the response: a = 0. 0009 0. 0037 0. 0056 0. 0037 0. 0009 b = 1 -2. 9768 3. 4223 -1. 7861 0. 3556 24 Nov'09 Comp 30291 DMP Section 5 49

A direct Form 2 implementation of 4 th order IIR filter x[n] + + 2. 977 -3. 422 z-1 + + 1. 79 -0. 356 z-1 0. 00093 0. 0037 0. 0056 0. 0037 + y[n] + + + 0. 00093 24 Nov'09 Comp 30291 DMP Section 5 50

Better ‘direct Form 2’ implementation of 4 th order IIR filter x[n] + + 0. 00093 2. 977 z-1 + 4 -3. 422 y[n] + z-1 + + 6 z-1 + 1. 79 -0. 356 24 Nov'09 z-1 Comp 30291 DMP Section 5 4 + 51

Cascaded bi-quad sections • Higher order IIR digital filters not normally implemented in Direct Form 1 or 2. • Instead, implement as cascaded biquad (sos) sections by typing: [a b] = butter(4, 0. 125); [sos G] = tf 2 sos(a, b) • MATLAB responds with: ‘transfer function’ to sos = 1 2 1 1 -1. 365 0. 478 ‘second order sections’ 1 2 1 1 -1. 612 0. 745 G = 0. 00093 24 Nov'09 Comp 30291 DMP Section 5 52

H(z) may be realised as: x[n] y[n] 0. 00093 1. 6 2 1. 36 2 -0. 74 -0. 48 Fourth order IIR Butterworth filter with cut -off fs/16 24 Nov'09 Comp 30291 DMP Section 5 53

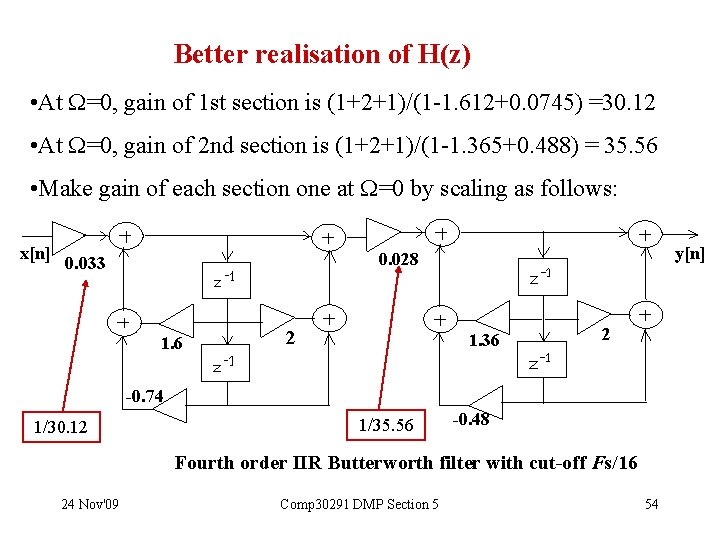
Better realisation of H(z) • At =0, gain of 1 st section is (1+2+1)/(1 -1. 612+0. 0745) =30. 12 • At =0, gain of 2 nd section is (1+2+1)/(1 -1. 365+0. 488) = 35. 56 • Make gain of each section one at =0 by scaling as follows: x[n] y[n] 0. 028 0. 033 1. 6 2 1. 36 2 -0. 74 1/30. 12 1/35. 56 -0. 48 Fourth order IIR Butterworth filter with cut-off Fs/16 24 Nov'09 Comp 30291 DMP Section 5 54

Gain-responses for 4 th order analog & IIR digital filter 24 Nov'09 Comp 30291 DMP Section 5 55

Compare gain-response of 4 th order Butt low-pass transfer function used as a prototype, with that of derived digital filter. • Both are 1 (0 d. B) at zero frequency. • Both are 0. 707 (-3 d. B) at the cut-off frequency. • Analogue gain approaches 0 as whereas digital filter gain becomes exactly zero at = . • Shape of Butt gain response is "warped" by bilinear transfn. • For digital filter, cut-off rate becomes sharper as because of the compression as . 24 Nov'09 Comp 30291 DMP Section 5 56

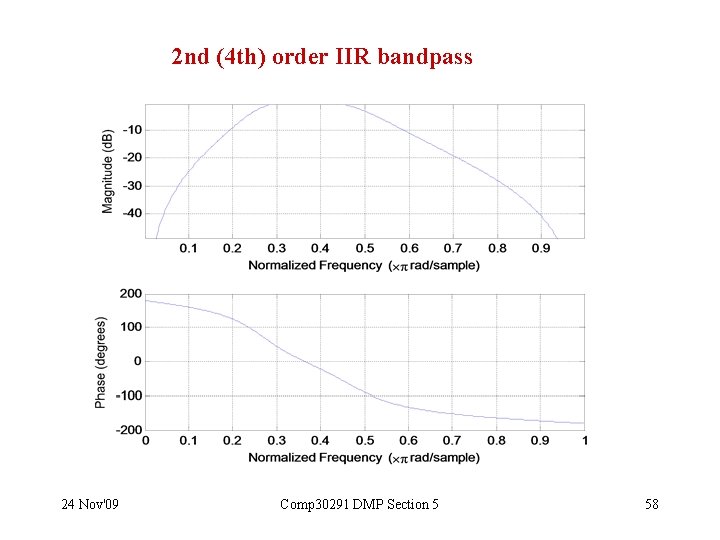
High-pass band-pass and band-stop IIR filters Example: 2 nd (4 th)order bandpass filter with L = /4 , u = /2. Solution: [a b] = butter(2, [0. 25 0. 5]) a = 0. 098 0 -0. 195 0 0. 098 b = 1 -1. 219 1. 333 -0. 667 0. 33 freqz(a, b); [sos G] = tf 2 sos(a, b) sos = 1 2 1 1 -0. 1665 0. 5348 1 -2 1 1 -1. 0524 0. 6232 G = 0. 098 Many people call this 4 th order - MATLAB calls it 2 nd order. 24 Nov'09 Comp 30291 DMP Section 5 57

2 nd (4 th) order IIR bandpass 24 Nov'09 Comp 30291 DMP Section 5 58

Arranged as 2 biquad sections x[n] y[n] 1 0. 1 . 17 -2 1. 05 2 -0. 54 -0. 62 24 Nov'09 Comp 30291 DMP Section 5 59

Higher order band-stop IIR filter Example: 4 th (8 th)order bandpass filter with L = /4 , u = /2. Solution: [a b] = butter(4, [0. 25 0. 5], ’stop’) a = 0. 35 -1. 15 2. 815 -4. 24 5. 1 -4. 24 2. 815 -1. 15 0. 35 b = 1 -2. 472 4. 309 -4. 886 4. 477 -2. 914 1. 519 -0. 5 0. 12 freqz(a, b); [sos G] = tf 2 sos(a, b) sos =1 -. 828 1 1 -0. 351 0. 428 1 -. 828 1 1 -0. 832 0. 49 1 -. 828 1 1 -0. 046 0. 724 1 -0. 828 1 1 -1. 244 0. 793 G = 0. 347 24 Nov'09 Comp 30291 DMP Section 5 60

Gain & phase resp of IIR band-stop filter 24 Nov'09 Comp 30291 DMP Section 5 61

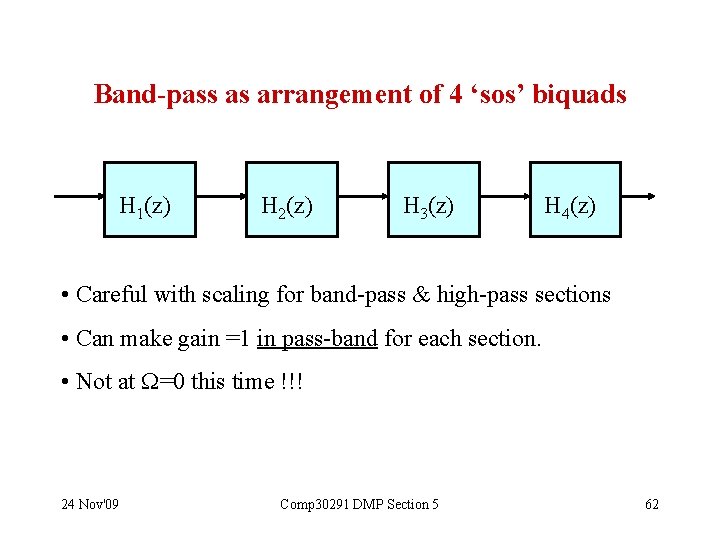
Band-pass as arrangement of 4 ‘sos’ biquads H 1(z) H 2(z) H 3(z) H 4(z) • Careful with scaling for band-pass & high-pass sections • Can make gain =1 in pass-band for each section. • Not at =0 this time !!! 24 Nov'09 Comp 30291 DMP Section 5 62

Transfer-function to second order sections: ‘tf 2 sos’ • . Must use [sos G] = tf 2 sos ([a 4 a 3 a 2 a 1 a 0], [b 4 … b 0 ]) • ‘help tf 2 sos’ to find out abt this function 24 Nov'09 Comp 30291 DMP Section 5 63

Wide-band-pass & band-stop filters • Option of cascading high pass & low-pass digital filters to give band-pass or band-stop filters must be used with care. • It is much simpler & avoids the factorisation problem. • Then make sure that analogue prototype is wide-band • High-pass IIR filters are designed by: [a b] = butter(4, 0. 125, ’high’); 24 Nov'09 Comp 30291 DMP Section 5 64

Comparison of IIR and FIR digital filters Advantage of IIR type digital filters: Economical in use of delays, multipliers and adders. Disadvantages: (1) Sensitive to coefficient round-off inaccuracies & effects of overflow in fixed point arith. These effects can lead to instability or serious distortion. (2) An IIR filter cannot be exactly linear phase. 24 Nov'09 Comp 30291 DMP Section 5 65

Advantages of FIR filters: (1) may be realised by non-recursive structures which are simpler and more convenient for programming especially on devices specifically designed for DSP. (2) FIR structures are always stable. (3) Because there is no recursion, round-off and overflow errors are easily controlled. (4) An FIR filter can be exactly linear phase. Disadvantage of FIR filters: Large orders can be required to perform fairly simple filtering tasks. 24 Nov'09 Comp 30291 DMP Section 5 66

Problems 1 Find H(z) for the following difference equations (a) y[n] = 2 x[n] - 3 x[n-1] + 6 x[n-4] (b) y[n] = x[n-1] - y[n-1] - 0. 5 y[n-2] 2 Show that passing {x[n]} thro’ H(z) = z - 1 produces {x[n-1]}. 3 Calculate the impulse-response of the digital filter with 1 H(z) = 1 - 2 z - 1 Draw its signal flow graph, plot its poles and zeros and comment on them. 24 Nov'09 Comp 30291 DMP Section 5 67

4. If LTI systems L 1 & L 2, with imp-responses {h 1[n]} & {h 2[n]} are arranged as below, calculate overall impulse- response. Show that this is affected by interchanging L 1 & L 2. 5. Low-pass IIR digital filter required with cut-off at f s/4 & stop-band attenuation at least 20 d. B for all frequencies above 3 f s /8 & below f s /2. Design by bilinear transfn using MATLAB. 24 Nov'09 Comp 30291 DMP Section 5 68

6. Design a 4 th order band-pass IIR digital filter with lower & upper cut-off frequencies at 300 Hz & 3400 Hz when f. S = 8 k. Hz. 7. Design a 4 th order band-pass IIR digital filter with lower & upper cut-off frequencies at 2000 Hz & 3000 Hz when f. S = 8 k. Hz. 8. What limits how good a notch filter we can implement on a fixed point DSP processor? In theory we can make notch sharper & sharper by moving the -3 d. B points closer & closer. What limits us in practice? How sharp a notch could we could get in 16 -bit fixed pt arithmetic? 9. What order of FIR low-pass filter would be required to be approx as good as the 2 nd order IIR low-pass filter ( /4 cut-off) designed in these notes? 24 Nov'09 Comp 30291 DMP Section 5 69