Unifying Theories of Concurrency CCS and CSP He

Unifying Theories of Concurrency: CCS and CSP He Jifeng and Tony Hoare BCTCS April 6, 2006

Why? • just for the sake of it – as a scientific achievement • to explain differences between theories – and what they are good for • to integrate more general toolsets – for coherence and consistency – in system design, implementation, . . .

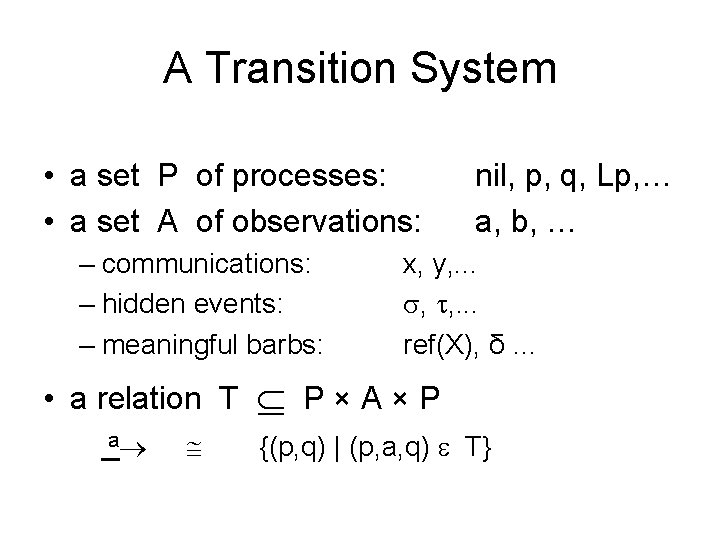
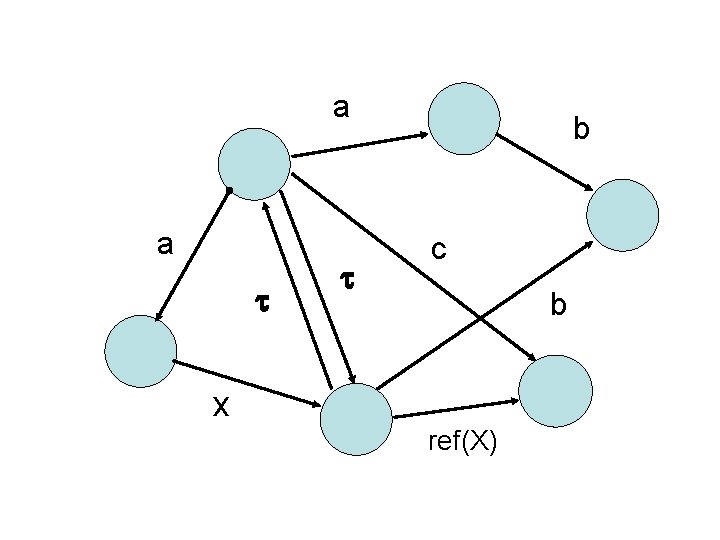
A Transition System • a set P of processes: • a set A of observations: – communications: – hidden events: – meaningful barbs: • a relation T a nil, p, q, Lp, … a, b, … x, y, . . . , , . . . ref(X), δ … P×A×P {(p, q) | (p, a, q) T}

a a b c b x ref(X)

Traces p=q q. p _ q. p • traces(p) {s|p • p q • p <a>s • p s r q & q a s s q _} s r

(Strong) Simulation • ≤ is the weakest x P×P such that a: A, x ; a a ; x – describes efficient model checking algorithm • ≡ ≤ ∩ ≥ Theorem: ≤ and ≡ are pre-orders – Id and ≤ ; ≤ satisfy the defining equation

Refinement ⊑ is the weakest x P×P such that s: A*, Theorem: x; ≤ s s ; U ⊑ – one defining equation implies the other Theorem: p ⊑ q iff traces(q) traces(p)

L: P→P • is a link if it maps all processes of its source theory to all processes of its target theory. • ≤L • ⊑L – i. e. , L ; ≤ ; L p ≤Lq iff Lp ≤ Lq L ; ⊑ ; L • Theorem: ≤ L , ⊑ L are preorders – L ; L = Id

L is monotonic ≤ ≤L or equivalently: – – p ≤ q ≤ ; L Lp ≤ Lq , all p, q L; ≤ consequently: – all order-theorems of source theory are valid in the target theory

L is idempotent L; L; ≤ = L; ≤ or equivalently: – L(Lp) ≡ Lp , all p consequently: – ≤L – Lp = ≡ ≤ (restricted to target theory) p iff p is in target theory

L is decreasing L ≤ or equivalently: – Lp ≤ p , for all p – ≤ L; ≤ consequently: – the target theory is more abstract – Lp is the closest abstraction of p within the target theory.

L is efficient L; ≤ = ≤L or equivalently: – Lp ≤ q iff Lp ≤ Lq , all p, q consequently: – to test : spec ≤ L imp, model-check : L(spec) ≤ imp, – (as is done in FDR)

L is a retraction iff • it is decreasing • it is idempotent • it is monotonic Theorem: iff ≤ L; L; ≤ ≤; L L is a retraction L is efficient L ; ≤ is a preorder L; ≤

quarter of the proof • L is a retraction (L ; ≤) is a preorder – Id (≤) (L ; ≤) – (L ; ≤ ; L ; ≤) (L ; ≤ ; ≤) L; ≤ {L dec} {L mon} {L idem}

Weak Simulation p =a=> q -----------Wp <a> Wq where = => and =a=> * * for a < > < > … * <a> * Theorem: W is a retraction

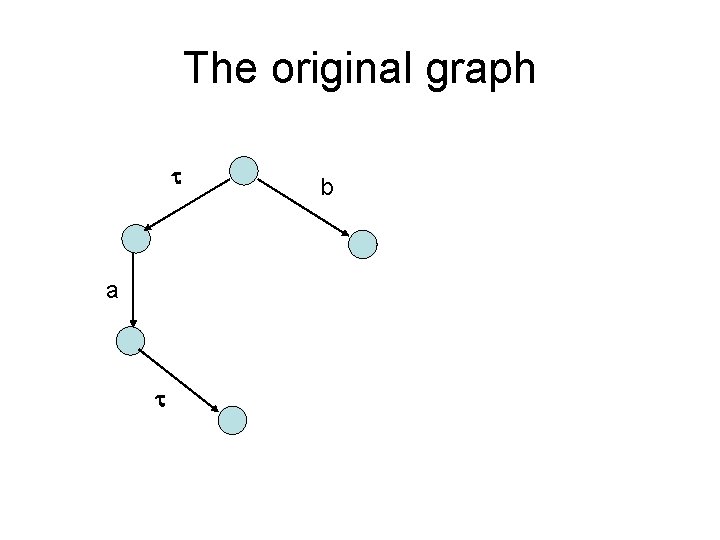
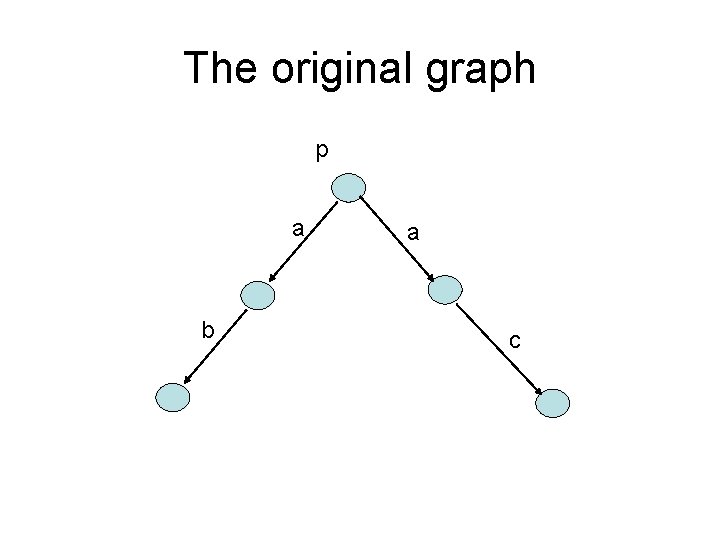
The original graph a b

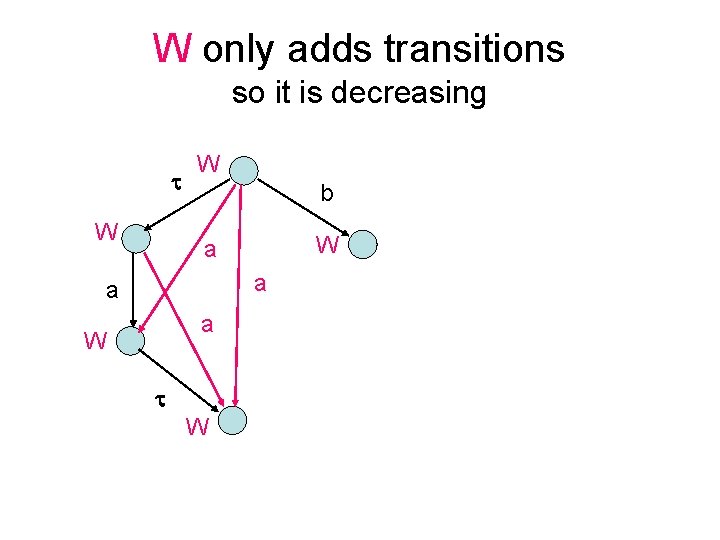
W only adds transitions so it is decreasing W W b W a a W W

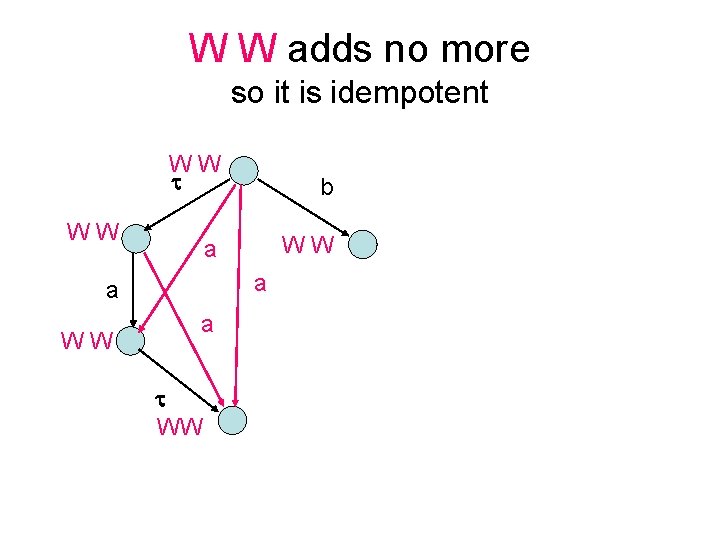
W W adds no more so it is idempotent WW b a WW WW a a WW a WW

(W; ≤ ) is weak simulation Theorem: it is the weakest solution of the defining equations –x; – x; <a> * <a> * * ; x, for a ; x • CCS/weak simulation is a retract (by W) of CCS/strong simulation

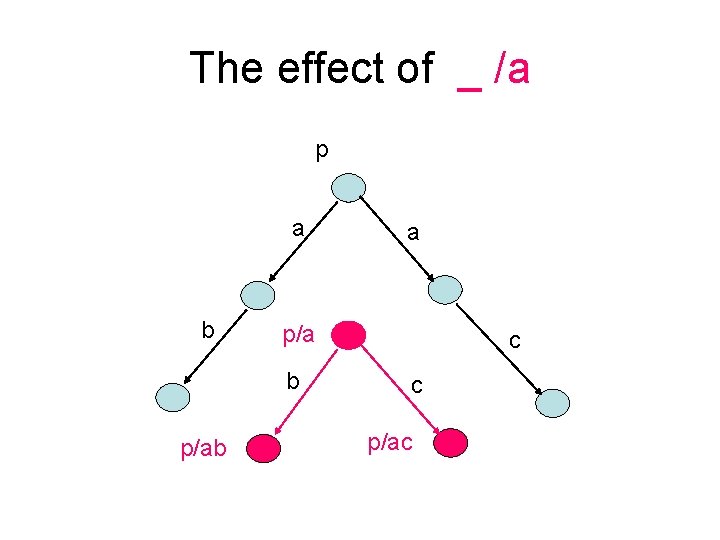
After • p/s is the most general behaviour of p after performing all of trace s p s <a> _ -----------p/s a p/(s<a>)

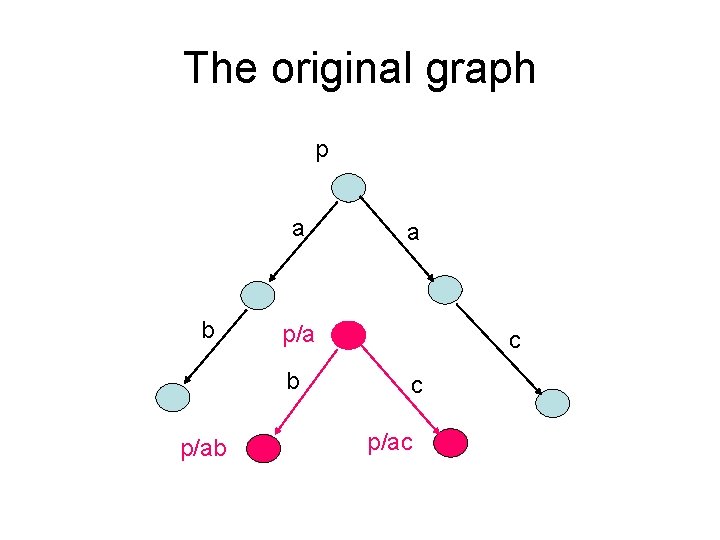
The original graph p a b a c

The effect of _ /a p a b p/ab a c c p/ac

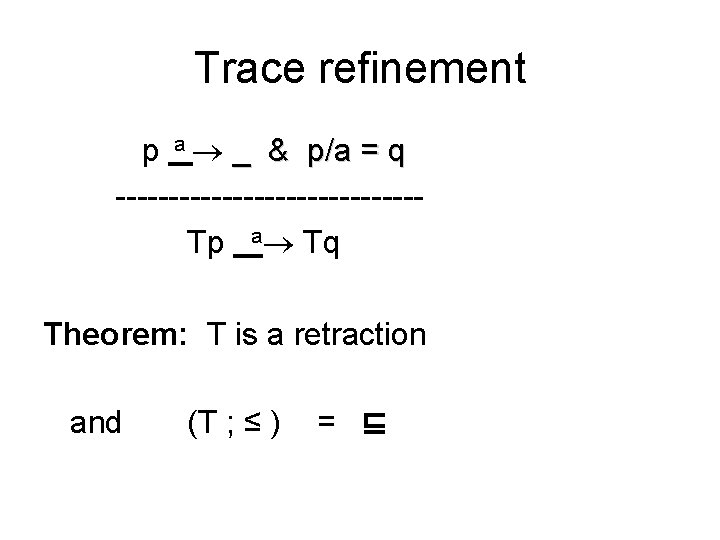
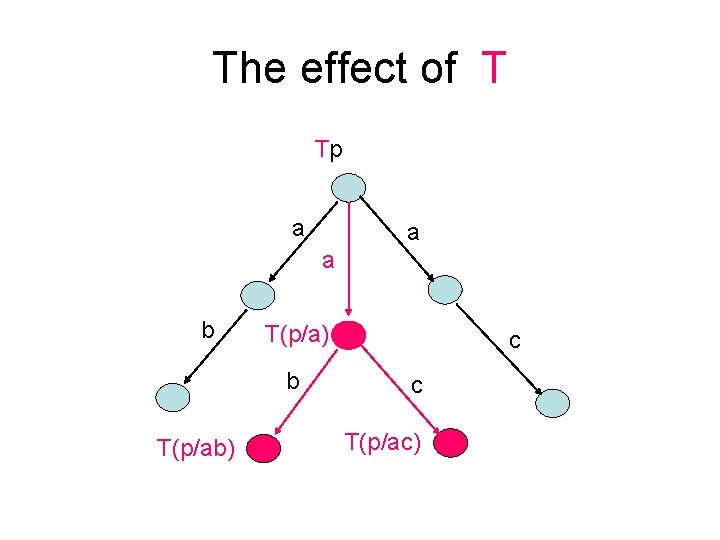
Trace refinement p a _ & p/a = q --------------Tp a Tq Theorem: T is a retraction and (T ; ≤ ) = ⊑

The original graph p a b p/ab a c c p/ac

The effect of T Tp a a a b T(p/a) b T(p/ab) c c T(p/ac)

CSP is a retract of CCS Theorem: (W; T) is a retraction and (W; T; ≤) is CSP trace refinement Conclusion: CSP/trace refinement is a retract of CCS/weak simulation.

ref(X) is a refusal where X is a set of communications x X { } p x _ ----------Rp ref(X) Rp Theorem: (R ; ≤ ; R ) p x q -------Rp x Rq is ⅔ simulation

Divergences p p'' … forever ---------------------Dp δ Dr & Dp a Dr p a q -------Dp a Dq Theorem: D is a retraction

CSP/FDR = L(CCS /≤) • where L = D ; R ; W ; T is a retraction – with respect to ≤D; R • L is defined by SOS transition rules. • CSP healthiness conditions are expressed p ≡ L(p) • CSP refinement coincides with simulation • variations of CSP and CCS defined by selection from: T, D, R, W, …

CCS • is more general – applies to all edge-labelled graphs • has less laws – the minimum reasonable set • is less expressive – uses equivalence rather than ordering

CSP • describes distributed computing – graphs restricted by healthiness conditions • has more laws – for optimisation and reasoning – the maximum reasonable set respecting deadlock and divergence • is more expressive – ordering represents correctness – and refinement of system from specification