Una sferetta P viene posta in una conca

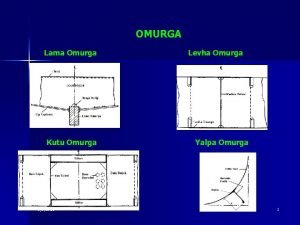
Una sferetta P viene posta in una conca semisferica di raggio R in un punto diverso da quello più basso. La sferetta rotola e l’angolo q indicato in figura varia con la legge: Quali sono le dimensioni di w e S? Qual è l’interpretazione geometrica di S? R P q L’argomento della funzione coseno è un angolo, cioè una grandezza adimensionale. wt deve essere adimensionale. [wt]= [w] [T]= [T 0] Risulta [w] = [T-1] L’angolo non ha dimensioni: pertanto [S] [R-1][cos]=[L 0 M 0 T 0] La funzione coseno è adimensionale, il raggio R ha le dimensioni di lunghezza [R]=[L]. Pertanto: [S]=[L] S è l’arco di cerchio tra P e il punto più basso della conca. G. M. - Edile A 2002/03

Data una colonna di liquido di densità r ed altezza h. La quantità rgh con g l’accelerazione di gravità, può essere una forza? La forza (F=ma) ha le dimensioni [F]=[M][LT-2] Quali sono le dimensioni di rgh? r è una densità [r]=[ML-3] g è un’accelerazione [g]=[LT-2] h è un’altezza [h]=[L] Pertanto [rgh ]= [ML-3] [LT-2] [L]=[ML-1 T-2] rgh non è una forza!! Confrontando le dimensioni di rgh con quelle della forza, si vede che rgh ha le dimensioni di una forza per una lunghezza alla meno 2 [F][L-2] Ma anche la pressione ha le stesse dimensioni! rgh potrebbe essere una pressione. rgh rappresenta l’aumento di pressione in un liquido con la profondità. G. M. - Edile A 2002/03

Il campione del kilogrammo ha la forma di un cilindro di altezza pari al diametro. Si dimostri che a parità di volume e di forma, queste dimensioni forniscono la minima area; ciò consente di minimizzare gli effetti della contaminazione superficiale. G. M. - Edile A 2002/03

Il campione del kilogrammo ha la forma di un cilindro di altezza pari al diametro. Si dimostri che a parità di volume e di forma, queste dimensioni forniscono la minima area; ciò consente di minimizzare gli effetti della contaminazione superficiale. Applica zione G. M. - Edile A 2002/03

Abbiamo espresso la superficie del cilindro in funzione del suo volume e del rapporto e tra il raggio e l’altezza Applica zione cont. Poiché il volume del cilindro deve rimanere costante, deve contenere sempre la stessa massa, possiamo limitarci a studiare la dipendenza da e. La superficie sarà minima quando f(e) sarà minima. Abbiamo visto che nei punti di massimo o di minimo relativo derivata si annulla. Cerchiamo e in cui G. M. - Edile A 2002/03

Calcoliamoci la derivata: Applica zione cont. Imponendo che la derivata sia nulla: Da cui G. M. - Edile A 2002/03

Applica zione cont. G. M. - Edile A 2002/03

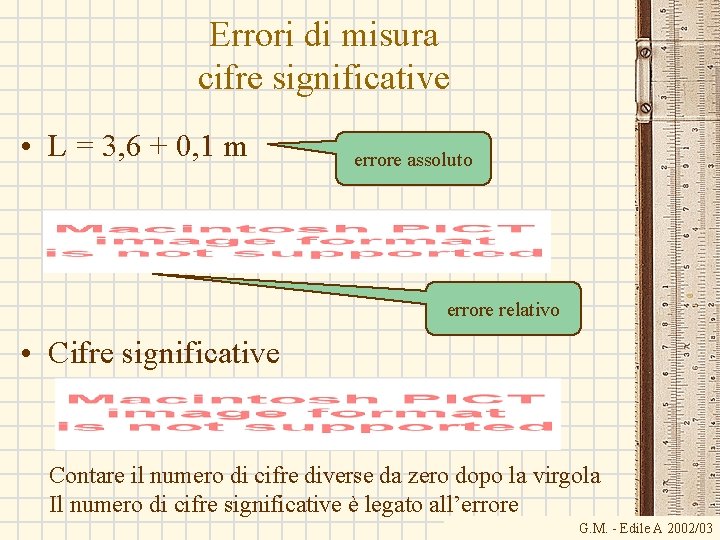
Errori di misura cifre significative • Ogni misura è affetta da errori – Errori casuali – Errori sistematici • L = 3, 6 + 0, 1 m valore errore scritto esplicitamente • Oppure L = 3, 6 m 2 cifre significative L’errore (implicito) è sull’ultima cifra (0, 1 m) G. M. - Edile A 2002/03

Errori di misura cifre significative • L = 3, 6 + 0, 1 m errore assoluto errore relativo • Cifre significative Contare il numero di cifre diverse da zero dopo la virgola Il numero di cifre significative è legato all’errore G. M. - Edile A 2002/03

Grandezze derivate: propagazione degli errori • Se la grandezza derivata si ottiene come somma o differenza di altre grandezza – L’errore non può essere più piccolo del più grande degli errori assoluti • Se la grandezza derivata si ottiene attraverso operazioni di prodotto o divisione di altre grandezze – L’errore relativo non deve essere più piccolo del più grande degli errori relativi. G. M. - Edile A 2002/03

Sistema di riferimento su una retta • Per definire un asse di riferimento occorre: – fissare l’origine – fissare il verso positivo • La posizione (coordinata) x del punto P sarà • La distanza di P dall’origine O se P viene dopo O percorrendo l’asse nel verso fissato () • Meno la distanza di P’ dall’origine O se P’ viene prima di O percorrendo l’asse nel verso fissato (x=-d. P’O) x = -d. P’O P’ x = +d. PO P G. M. - Edile A 2002/03

Sistema di riferimento nel piano • Occorrono due assi cartesiani (ortogonali) (stessa origine) – L’asse x deve ruotare di 90° in senso antiorario per sovrapporsi all’asse y • Il punto P nel piano sarà individuato dalle coordinate x, y, che sono le coordinate dei punti proiezione di P rispettivamente sugli assi x e y • I punti proiezioni Px e Py si ottengono mandando le perpendicolari da P rispettivamente agli assi x (verde) ed y (violetta). G. M. - Edile A 2002/03

Rappresentazione polare Asse y • La posizione di P nel piano può essere specificata in coordinate polari (r, q) • r è la distanza di P dall’origine del sistema di riferimento. P r q O Asse x • q è l’angolo formato dal segmento OP con un asse arbitrariamente fissato nel piano Asse y P y r q O x • r è un numero reale positivo Asse x • Nella figura è stato scelto l’asse x come asse di riferimento. • L’angolo q è positivo se l’asse di riferimento x deve ruotare in verso antiorario per sovrapporsi al segmento OP. G. M. - Edile A 2002/03

Sistema di riferimento nello spazio • Nello spazio occorrono tre assi orientati, x, y, z, ortogonali tra di loro. • Si usano terne destrorse, cioè con l'asse x disposto secondo il pollice, l'asse y secondo l'indice, e quello z secondo il medio della mano destra. • Si manda da P la parallela all'asse z fino ad incontrare il piano xy: si determina così il punto Pxy proiezione di P sul piano xy. • Si congiunge con un segmento l'origine O con il punto Pxy. Il segmento OPxy è perpendicolare all’asse z. • La proiezione di P sull'asse z, Pz, si determina mandando da P un segmento parallelo al segmento OPxy. • La proiezione Px di P sull'asse x si determina mandando da Pxy la parallela all'asse y fino ad intersecare l'asse x • La proiezione Py di P sull'asse y si determina mandando da Pxy la parallela all'asse x fino ad intersecare l'asse y. G. M. - Edile A 2002/03

Grandezze scalari e vettoriali • • • Massa Tempo Temperatura Pressione Posizione lungo un asse (linea) • Volume • Lavoro • Energia • • Posizione nel piano Posizione nello spazio Velocità Accelerazione Forza Quantità di moto Impulso Momento della quantità di moto G. M. - Edile A 2002/03

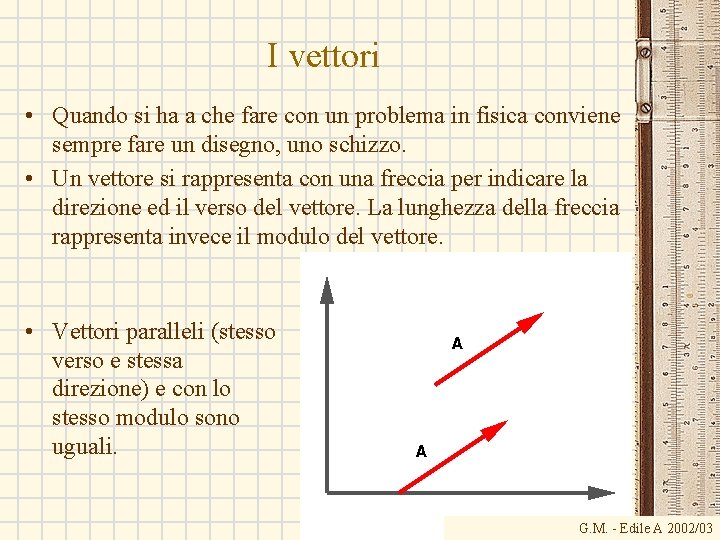
I vettori • Quando si ha a che fare con un problema in fisica conviene sempre fare un disegno, uno schizzo. • Un vettore si rappresenta con una freccia per indicare la direzione ed il verso del vettore. La lunghezza della freccia rappresenta invece il modulo del vettore. • Vettori paralleli (stesso verso e stessa direzione) e con lo stesso modulo sono uguali. G. M. - Edile A 2002/03

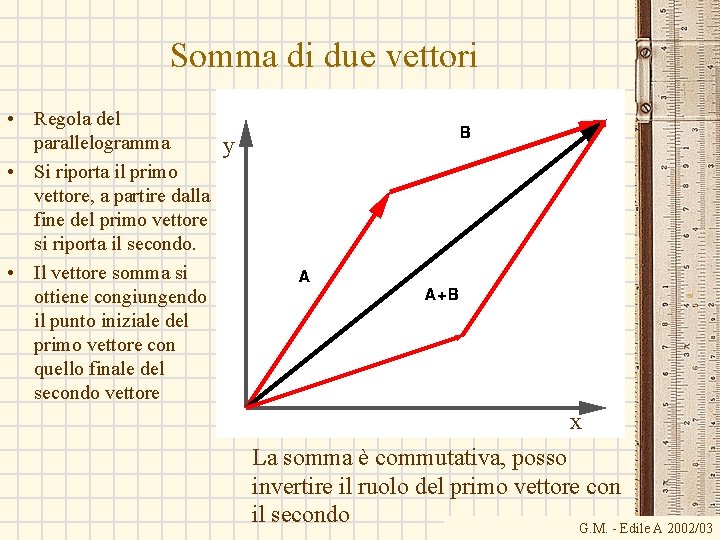
Somma di due vettori • Regola del parallelogramma y • Si riporta il primo vettore, a partire dalla fine del primo vettore si riporta il secondo. • Il vettore somma si ottiene congiungendo il punto iniziale del primo vettore con quello finale del secondo vettore x La somma è commutativa, posso invertire il ruolo del primo vettore con il secondo G. M. - Edile A 2002/03

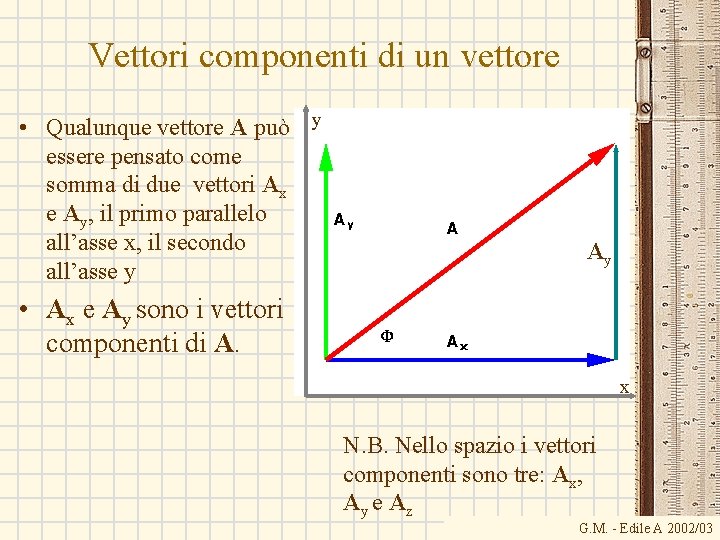
Vettori componenti di un vettore • Qualunque vettore A può y essere pensato come somma di due vettori Ax e Ay, il primo parallelo all’asse x, il secondo all’asse y Ay • Ax e Ay sono i vettori componenti di A. x N. B. Nello spazio i vettori componenti sono tre: Ax, Ay e Az G. M. - Edile A 2002/03

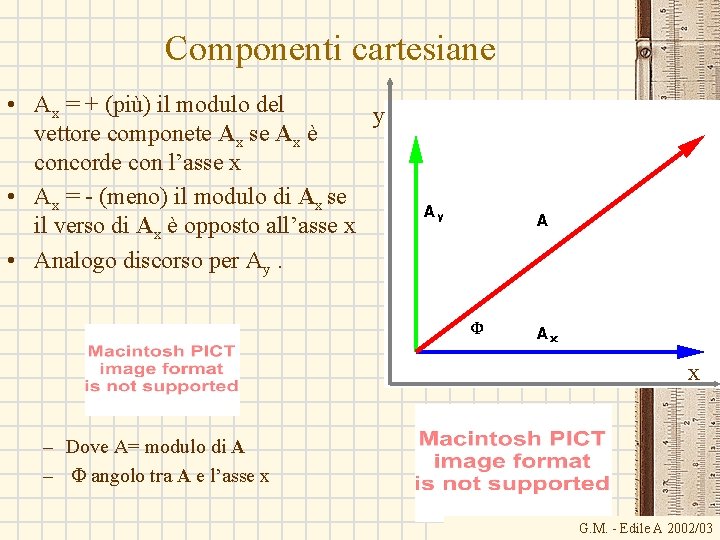
Componenti cartesiane • Ax = + (più) il modulo del y vettore componete Ax se Ax è concorde con l’asse x • Ax = - (meno) il modulo di Ax se il verso di Ax è opposto all’asse x • Analogo discorso per Ay. x – Dove A= modulo di A – F angolo tra A e l’asse x G. M. - Edile A 2002/03

Somma di vettori usando le componenti Ax Bx G. M. - Edile A 2002/03

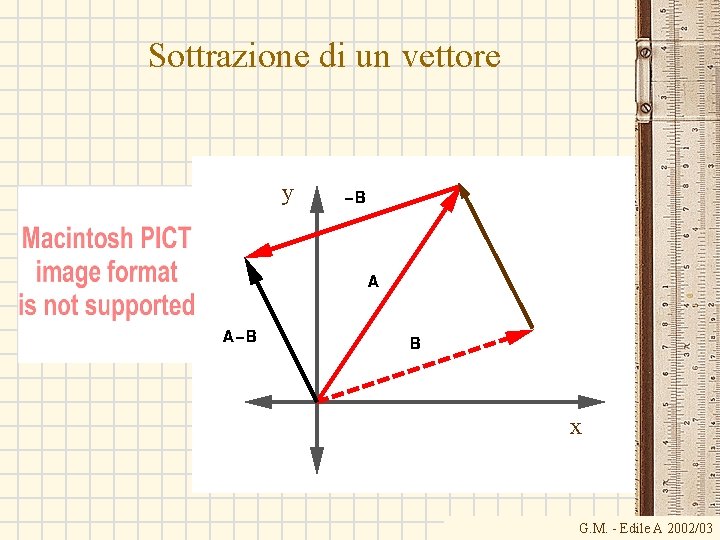
Sottrazione di un vettore y x G. M. - Edile A 2002/03

Versori A • Sono vettori di modulo unitario • I versori non hanno dimensioni – Se u. A è il versore del vettore A, allora u. A A=Au. A • I versori degli assi x, y, e z si chiamano rispettivamente: i, j (e k), oppure ux, uy e uz. – Nel caso – Ax=Axi – Ay=Ayj y • A = Ax+ Ay= Axi+ Ayj A j i Ay Ax x G. M. - Edile A 2002/03

Significato di una relazione vettoriale Due vettori sono uguali se sono uguali le componenti Un’equazione vettoriale corrisponde a due (nel piano), tre (nello spazio) equazioni scalari G. M. - Edile A 2002/03

Un’automobile viaggia verso est per 50 km, poi verso nord per 30 km e infine in direzione di 30° a est rispetto al nord per 25 km. Si disegni il diagramma dei vettori e si determini lo spostamento totale dell’auto dal punto di partenza. Applic azione G. M. - Edile A 2002/03

La lancetta dei minuti di un orologio a parete misura 10 cm dall’asse alla punta. Qual è il vettore spostamento della punta dal quarto d’ora alla mezz’ora durante la mezz’ora successiva durante l’ora successiva Applic azione G. M. - Edile A 2002/03

Il vettore B sommato al vettore A da per risultato 6. 0 i+1. 0 j. Se si sottrae B da A il risultato è -4. 0 i+7. 0 j. Quant’è il modulo di A. Applic azione G. M. - Edile A 2002/03

Sono date le componenti di 4 vettori a, b, c, d. Determinare per ciascuno di essi l’angolo formato con l’asse delle x: 1) ax=3 ay=3 2) bx=-3 by=-3 3) cx=-3 cy=3 4) dx=3 dy=-3 Applic azione G. M. - Edile A 2002/03