Type checking and inference Using the type constraints










- Slides: 12

Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-II: Construct type equations. The rules: 1. Atomic expressions / primitiveprocedures: Construct equations using their types. 2. Lambda expressions: For (lambda (v 1. . . vn) e 1. . . em), construct: 3. Application expressions: For (f e 1. . . en), construct: Expression Equation sqrt 4 Tsqrt : = [Number → Number] Tnum 4: =Number T 1: =[Tnum 4*Tsqrt→T 0] T 1: =[Tf*Tx→T 2] Tf: =[Tx→T 2] ((lambda (f x)) 4 sqrt) (lambda (f x)) (f x) Expression Var ((lambda(f x)) 4 sqrt) (lambda(f x) f x 4 T 0 T 1 T 2 Tf Tx Tnum 4 sqrt Tsqrt

Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 1. T 1=[Tnum 4*Tsqrt→T 0] 2. T 1=[Tf*Tx→T 2] 3. Tf=[Tx→T 2] 4. Tsqrt = [Number → Number] 5. Tnum 4=Number Equation 1: - Initially, the substitution is empty. Step 1 is ignored. - Eq 1 is moved to the substitution.

Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 2. T 1=[Tf*Tx→T 2] 3. Tf=[Tx→T 2] 4. Tsqrt = [Number → Number] 5. Tnum 4=Number T 1: =[Tnum 4*Tsqrt→T 0] Equation 1: - Initially, the substitution is empty. Step 1 is ignored. - Eq 1 is moved to the substitution.

Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 2. T 1=[Tf*Tx→T 2] 3. Tf=[Tx→T 2] 4. Tsqrt = [Number → Number] 5. Tnum 4=Number T 1: =[Tnum 4*Tsqrt→T 0] Equation 2: - Apply step 1: T 1 is replaced by current substitution: [Tf* Tx -> T 2] = [Tnum 4 * Tsqrt-> T 0] - Both side are composite, apply step 5: Equations are split and Eq 2 is removed.

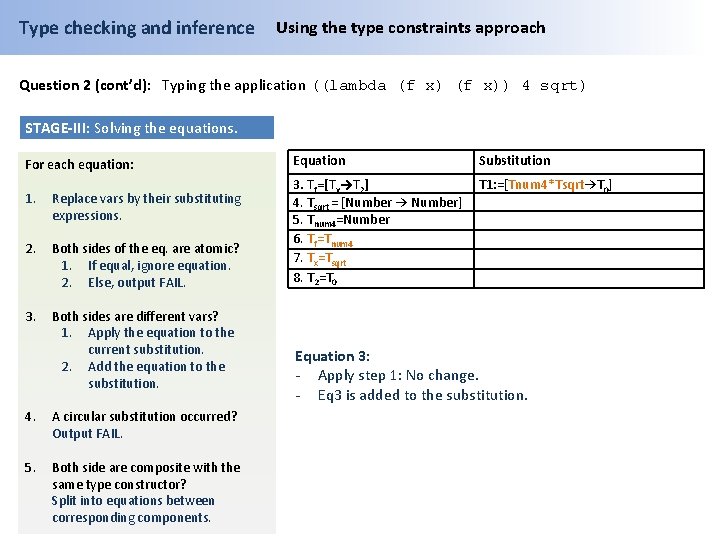
Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 3. Tf=[Tx→T 2] 4. Tsqrt = [Number → Number] 5. Tnum 4=Number 6. Tf=Tnum 4 7. Tx=Tsqrt 8. T 2=T 0 T 1: =[Tnum 4*Tsqrt→T 0] Equation 2: - Apply step 1: T 1 is replaced by current substitution: [Tf* Tx -> T 2] = [Tnum 4 * Tsqrt-> T 0] - Both side are composite, apply step 5: Equations are split and Eq 2 is removed.

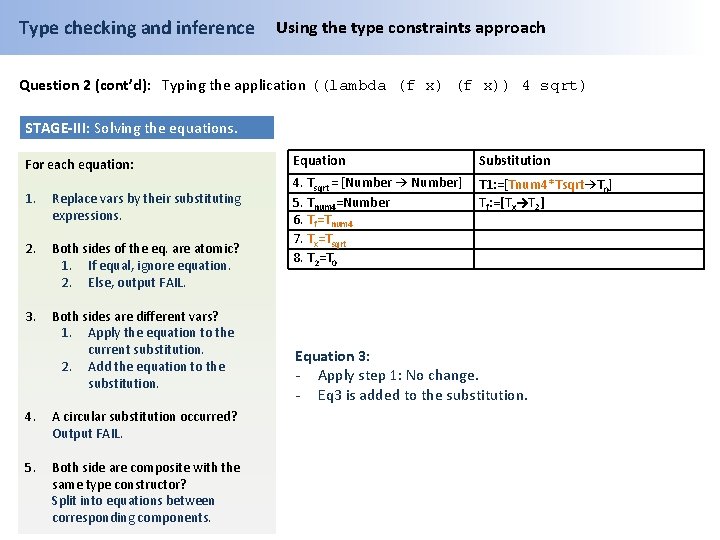
Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 3. Tf=[Tx→T 2] 4. Tsqrt = [Number → Number] 5. Tnum 4=Number 6. Tf=Tnum 4 7. Tx=Tsqrt 8. T 2=T 0 T 1: =[Tnum 4*Tsqrt→T 0] Equation 3: - Apply step 1: No change. - Eq 3 is added to the substitution.

Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 4. Tsqrt = [Number → Number] 5. Tnum 4=Number 6. Tf=Tnum 4 7. Tx=Tsqrt 8. T 2=T 0 T 1: =[Tnum 4*Tsqrt→T 0] Tf: =[Tx→T 2] Equation 3: - Apply step 1: No change. - Eq 3 is added to the substitution.

Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 4. Tsqrt = [Number → Number] 5. Tnum 4=Number 6. Tf=Tnum 4 7. Tx=Tsqrt 8. T 2=T 0 T 1: =[Tnum 4*Tsqrt→T 0] Tf: =[Tx→T 2] Equation 4: - Apply step 1: No change. - Eq 4 is added to the substitution: The substitution is updated by substituting Tsqrt for [Number → Number]

Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 5. Tnum 4=Number 6. Tf=Tnum 4 7. Tx=Tsqrt 8. T 2=T 0 T 1: =[Tnum 4* [Number → Number] →T 0] Tf: =[Tx→T 2] Tsqrt : = [Number → Number] Equation 4: - Apply step 1: No change. - Eq 4 is added to the substitution: The substitution is updated by substituting Tsqrt for [Number → Number]

Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 5. Tnum 4=Number 6. Tf=Tnum 4 7. Tx=Tsqrt 8. T 2=T 0 T 1: =[Tnum 4* [Number → Number] →T 0] Tf: =[Tx→T 2] Tsqrt : = [Number → Number] Equation 5: - Apply step 1: No change. - Eq 5 is added to the substitution: The substitution is updated by substituting Tnum 4 for Number

Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Solving the equations. For each equation: Equation Substitution 1. Replace vars by their substituting expressions. 6. Tf=Tnum 4 7. Tx=Tsqrt 8. T 2=T 0 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. T 1: =[Number* [Number → Number] →T 0] Tf: =[Tx→T 2] Tsqrt : = [Number → Number] Tnum 4: =Number 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation 5: - Apply step 1: No change. - Eq 5 is added to the substitution: The substitution is updated by substituting Tnum 4 for Number

Type checking and inference Using the type constraints approach Question 2 (cont’d): Typing the application ((lambda (f x)) 4 sqrt) STAGE-III: Solving the equations. For each equation: Equation Substitution 1. Replace vars by their substituting expressions. 6. Tf=Tnum 4 7. Tx=Tsqrt 8. T 2=T 0 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. T 1: =[Number* [Number → Number] →T 0] Tf: =[Tx→T 2] Tsqrt : = [Number → Number] Tnum 4: =Number 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation 6: - Apply step 1: Tf , Tnum 4 are replaced by current substitution: [Tx→T 2] = Number