Type checking and inference Using the type constraints

Type checking and inference • • • Using the type constraints approach Applications of typing axioms / rules are replaced with type equations. A solution to the equations assigns types for every sub-expression. A 4 -stages algorithm. Question 1: Typing the application ((lambda (f x)) sqrt 4) STAGE-I: Renaming STAGE-II: Assign type variables to all sub-expressions Expression Var ((lambda(f x)) sqrt 4) (lambda(f x)) T 0 T 1 T 2 Tf Tx Tsqrt Tnum 4 (f x) f x sqrt 4

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Construct type equations The rules: 1. Atomic expressions / primitiveprocedures: Construct equations using their types. Expression Equation sqrt 4 Tsqrt = [Number → Number] Tnum 4=Number T 1=[Tsqrt*Tnum 4→T 0] T 1=[Tf*Tx→T 2] Tf=[Tx→T 2] ((lambda (f x)) sqrt 4) (lambda (f x)) (f x) 2. Lambda expressions: For (lambda (v 1. . . vn) e 1. . . em), construct: Expression Var ((lambda(f x)) sqrt 4) (lambda(f x)) 3. Application expressions: For (f e 1. . . en), construct: (f x) f x sqrt 4 T 0 T 1 T 2 Tf Tx Tsqrt Tnum 4

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Construct type equations The rules: 1. Atomic expressions / primitiveprocedures: Construct equations using their types. Expression Equation sqrt 4 Tsqrt = [Number → Number] Tnum 4=Number T 1=[Tsqrt*Tnum 4→T 0] T 1=[Tf*Tx→T 2] Tf=[Tx→T 2] ((lambda (f x)) sqrt 4) (lambda (f x)) (f x) 2. Lambda expressions: For (lambda (v 1. . . vn) e 1. . . em), construct: Expression Var ((lambda(f x)) sqrt 4) (lambda(f x)) 3. Application expressions: For (f e 1. . . en), construct: (f x) f x sqrt 4 T 0 T 1 T 2 Tf Tx Tsqrt Tnum 4

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-IV: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 1. T 1=[Tsqrt*Tnum 4→T 0] 2. T 1=[Tf*Tx→T 2] 3. Tf=[Tx→T 2] 4. Tsqrt = [Number → Number] 5. Tnum 4=Number {} Equation 1: - Initially, the substitution is empty. Step 1 is ignored. - Eq 1 is moved to the substitution.

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 2. T 1=[Tf*Tx→T 2] 3. Tf=[Tx→T 2] 4. Tsqrt = [Number → Number] 5. Tnum 4=Number T 1: =[Tsqrt*Tnum 4→T 0] Equation 1: - Initially, the substitution is empty. Step 1 is ignored. - Eq 1 is moved to the substitution.

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 2. T 1=[Tf*Tx→T 2] 3. Tf=[Tx→T 2] 4. Tsqrt = [Number → Number] 5. Tnum 4=Number T 1: =[Tsqrt*Tnum 4→T 0] Equation 2: - Apply step 1: T 1 is replaced by current substitution: [Tsqrt* Tnum 4 -> T 0] = [Tf* Tx -> T 2] - Both side are composite, apply step 5: Equations are split and Eq 2 is removed.

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 3. Tf=[Tx→T 2] 4. Tsqrt = [Number → Number] 5. Tnum 4=Number 6. Tf=Tsqrt 7. Tx=Tnum 4 8. T 2=T 0 T 1: =[Tsqrt*Tnum 4→T 0] Equation 2: - Apply step 1: T 1 is replaced by current substitution: [Tsqrt* Tnum 4 -> T 0] = [Tf* Tx -> T 2] - Both side are composite, apply step 5: Equations are split and Eq 2 is removed.

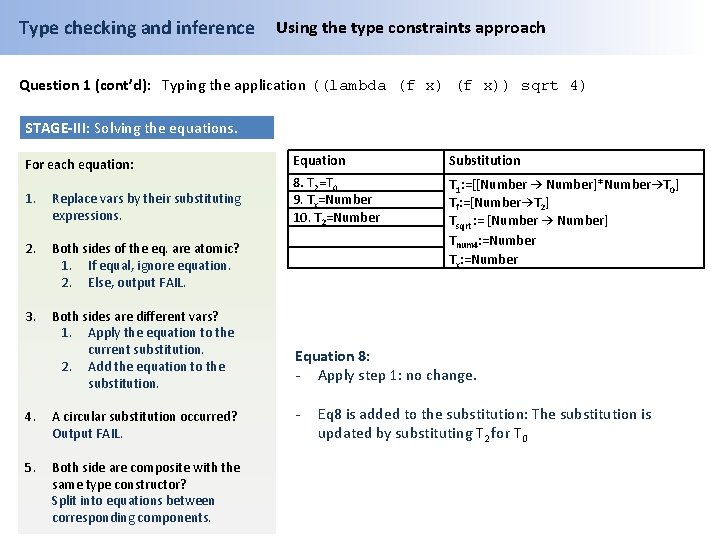
Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 3. Tf=[Tx→T 2] 4. Tsqrt = [Number → Number] 5. Tnum 4=Number 6. Tf=Tsqrt 7. Tx=Tnum 4 8. T 2=T 0 T 1: =[Tsqrt*Tnum 4→T 0] Equation 3: - Apply step 1: No change. - Eq 3 is added to the substitution.

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 4. Tsqrt = [Number → Number] 5. Tnum 4=Number 6. Tf=Tsqrt 7. Tx=Tnum 4 8. T 2=T 0 T 1: =[Tsqrt*Tnum 4→T 0] Tf: =[Tx→T 2] Equation 3: - Apply step 1: No change. - Eq 3 is added to the substitution.

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 4. Tsqrt = [Number → Number] 5. Tnum 4=Number 6. Tf=Tsqrt 7. Tx=Tnum 4 8. T 2=T 0 T 1: =[Tsqrt*Tnum 4→T 0] Tf: =[Tx→T 2] Equation 4: - Apply step 1: No change. - Eq 4 is added to the substitution: The substitution is updated by substituting Tsqrt for [Number → Number]

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 5. Tnum 4=Number 6. Tf=Tsqrt 7. Tx=Tnum 4 8. T 2=T 0 T 1: =[[Number → Number]*Tnum 4→T 0] Tf: =[Tx→T 2] Tsqrt : = [Number → Number] Equation 4: - Apply step 1: No change. - Eq 4 is added to the substitution: The substitution is updated by substituting Tsqrt for [Number → Number]

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 5. Tnum 4=Number 6. Tf=Tsqrt 7. Tx=Tnum 4 8. T 2=T 0 T 1: =[[Number → Number]*Tnum 4→T 0] Tf: =[Tx→T 2] Tsqrt : = [Number → Number] Equation 5: - Apply step 1: No change. - Eq 5 is added to the substitution: The substitution is updated by substituting Tnum 4 for Number

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: Equation Substitution 1. Replace vars by their substituting expressions. 6. Tf=Tsqrt 7. Tx=Tnum 4 8. T 2=T 0 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. T 1: =[[Number → Number]*Number→T 0] Tf: =[Tx→T 2] Tsqrt : = [Number → Number] Tnum 4: =Number 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation 5: - Apply step 1: No change. - Eq 5 is added to the substitution: The substitution is updated by substituting Tnum 4 for Number

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: Equation Substitution 1. Replace vars by their substituting expressions. 6. Tf=Tsqrt 7. Tx=Tnum 4 8. T 2=T 0 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. T 1: =[[Number → Number]*Number→T 0] Tf: =[Tx→T 2] Tsqrt : = [Number → Number] Tnum 4: =Number 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation 6: - Apply step 1: Tf , Tsqrt are replaced by current substitution: [Tx→T 2] = [Number → Number] - Both side are composite, apply step 5: Equations are split and Eq 6 is removed.

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 7. Tx=Tnum 4 8. T 2=T 0 9. Tx=Number 10. T 2=Number T 1: =[[Number → Number]*Number→T 0] Tf: =[Tx→T 2] Tsqrt : = [Number → Number] Tnum 4: =Number Equation 6: - Apply step 1: Tf , Tsqrt T 1 is replaced by current substitution: [Tx→T 2]=[Number → Number] - Both side are composite, apply step 5: Equations are split and Eq 6 is removed.

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 7. Tx=Tnum 4 8. T 2=T 0 9. Tx=Number 10. T 2=Number T 1: =[[Number → Number]*Number→T 0] Tf: =[Tx→T 2] Tsqrt : = [Number → Number] Tnum 4: =Number Equation 7: - Apply step 1: Tnum 4 is replaced by current substitution: Tx=Number - Eq 7 is added to the substitution: The substitution is updated by substituting Tx for Number

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: Equation Substitution 1. Replace vars by their substituting expressions. 8. T 2=T 0 9. Tx=Number 10. T 2=Number 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. T 1: =[[Number → Number]*Number→T 0] Tf: =[Number→T 2] Tsqrt : = [Number → Number] Tnum 4: =Number Tx: =Number 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation 7: - Apply step 1: Tnum 4 is replaced by current substitution: Tx=Number - Eq 7 is added to the substitution: The substitution is updated by substituting Tx for Number

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: Equation Substitution 1. Replace vars by their substituting expressions. 8. T 2=T 0 9. Tx=Number 10. T 2=Number 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. T 1: =[[Number → Number]*Number→T 0] Tf: =[Number→T 2] Tsqrt : = [Number → Number] Tnum 4: =Number Tx: =Number 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation 8: - Apply step 1: no change. - Eq 8 is added to the substitution: The substitution is updated by substituting T 2 for T 0

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: Equation Substitution 1. Replace vars by their substituting expressions. 9. Tx=Number 10. T 2=Number 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. T 1: =[[Number → Number]*Number→T 0] Tf: =[Number→T 0] Tsqrt : = [Number → Number] Tnum 4: =Number Tx: =Number T 2: =T 0 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation 8: - Apply step 1: no change. - Eq 8 is added to the substitution: The substitution is updated by substituting T 2 for T 0

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: Equation Substitution 1. Replace vars by their substituting expressions. 9. Tx=Number 10. T 2=Number 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. T 1: =[[Number → Number]*Number→T 0] Tf: =[Number→T 0] Tsqrt : = [Number → Number] Tnum 4: =Number Tx: =Number T 2: =T 0 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation 9: - Apply step 1: Tx is replaced by current substitution: Number=Number - Step 3: both sides are atomic types and the equation is ignored.

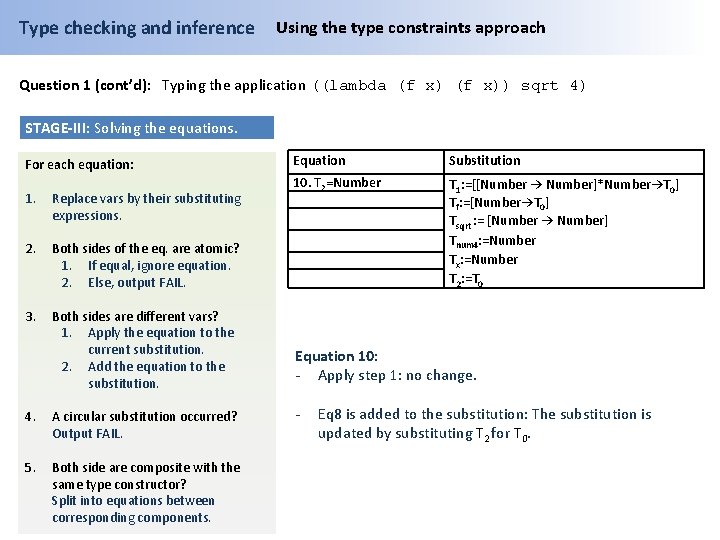
Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. 4. A circular substitution occurred? Output FAIL. 5. Both side are composite with the same type constructor? Split into equations between corresponding components. Equation Substitution 10. T 2=Number T 1: =[[Number → Number]*Number→T 0] Tf: =[Number→T 0] Tsqrt : = [Number → Number] Tnum 4: =Number Tx: =Number T 2: =T 0 Equation 10: - Apply step 1: no change. - Eq 8 is added to the substitution: The substitution is updated by substituting T 2 for T 0.

Type checking and inference Using the type constraints approach Question 1 (cont’d): Typing the application ((lambda (f x)) sqrt 4) STAGE-III: Solving the equations. For each equation: 1. Replace vars by their substituting expressions. 2. Both sides of the eq. are atomic? 1. If equal, ignore equation. 2. Else, output FAIL. 3. Both sides are different vars? 1. Apply the equation to the current substitution. 2. Add the equation to the substitution. Equation Substitution T 1: =[[Number → umber]*Number→Number] Tf: =[Number→Number] Tsqrt : = [Number → Number] Tnum 4: =Number Tx: =Number T 2: =Number T 0: =Number Equation 10: - Apply step 1: no change. 4. A circular substitution occurred? Output FAIL. - 5. Both side are composite with the same type constructor? Split into equations between corresponding components. The type inference succeeds. The inferred type is: Number Eq 8 is added to the substitution: The substitution is updated by substituting T 0 with Number.