Trigonometry www mathsplus ie Trigonometry Topics Radians Length


























![Q 1. . (ii) In the triangle ABC, D is a point on [BC]. Q 1. . (ii) In the triangle ABC, D is a point on [BC].](https://slidetodoc.com/presentation_image_h2/a60b235fa4d113d8a7b1bdbe44e0ece1/image-46.jpg)




![S P, Q and R are points on level ground, [SR] is a vertical S P, Q and R are points on level ground, [SR] is a vertical](https://slidetodoc.com/presentation_image_h2/a60b235fa4d113d8a7b1bdbe44e0ece1/image-53.jpg)
















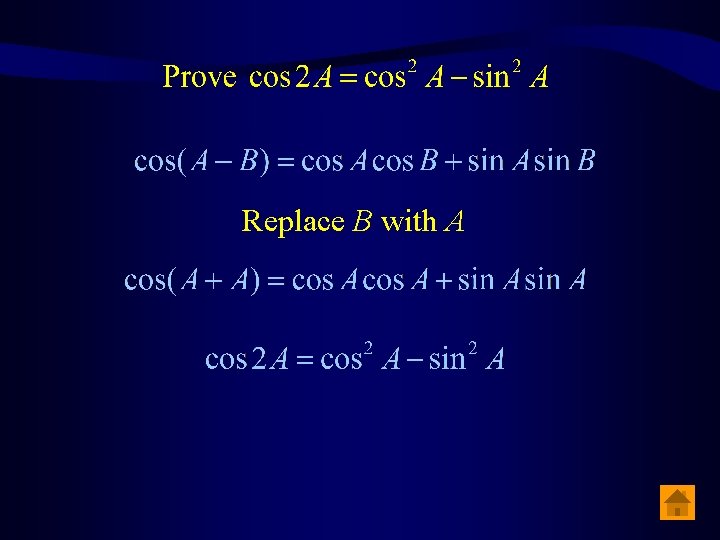


- Slides: 90

Trigonometry www. mathsplus. ie

Trigonometry Topics Radians/ Length of arc The Unit Circle Trigonometric Functions Larger Angles 3 D Trigonometry Trigonometric Identities Graphing Trig Functions

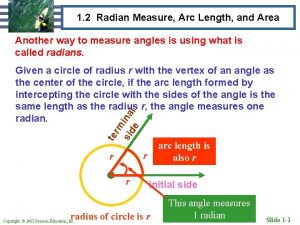
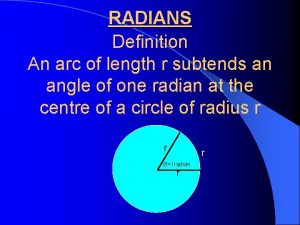
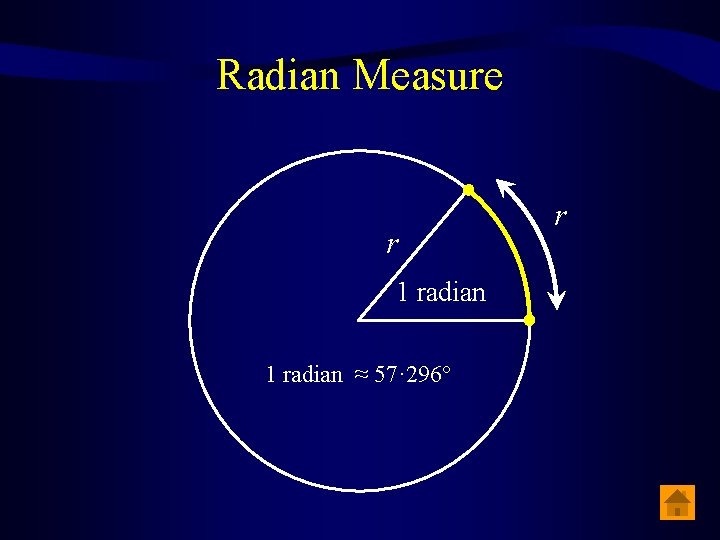
Radian Measure To talk about trigonometric functions, it is helpful to move to a different system of angle measure, called radian measure. A radian is the measure of a central angle whose minor arc is equal in length to the radius of the circle.

Radian Measure r 1 radian ≈ 57· 296° r

Radian Measure There are 2π radians in a full rotation – once around the circle There are 360° in a full rotation 2π = 360° π = 180° To convert from degrees to radians or radians to degrees, use the proportion degrees radians = o 180

Examples Find the degree measure equivalent of 3π radians. 4 3π 3 180 = 4 4 = 135° Find the radian measure equivalent of 210°. 180° = π π 1° = 180 210π 7π 210° = = 180 6

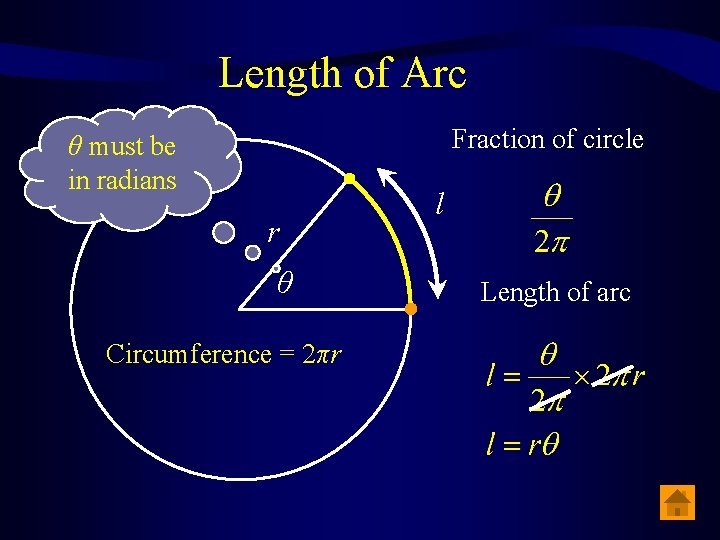
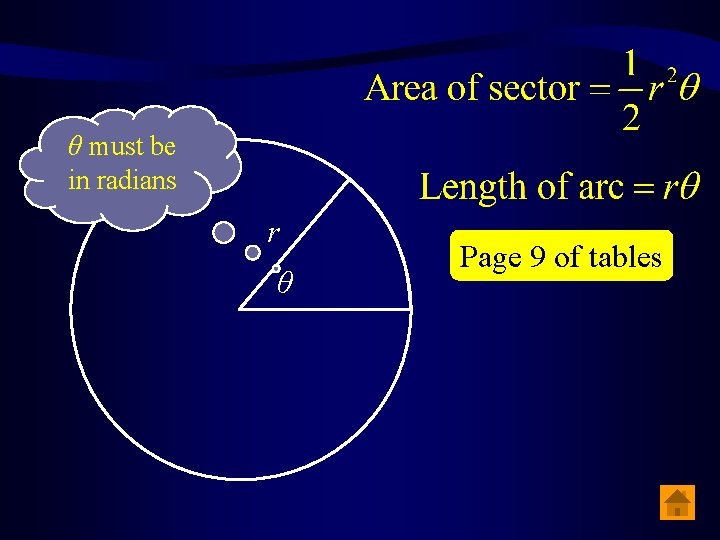
Length of Arc Fraction of circle θ must be in radians r θ Circumference = 2πr l Length of arc

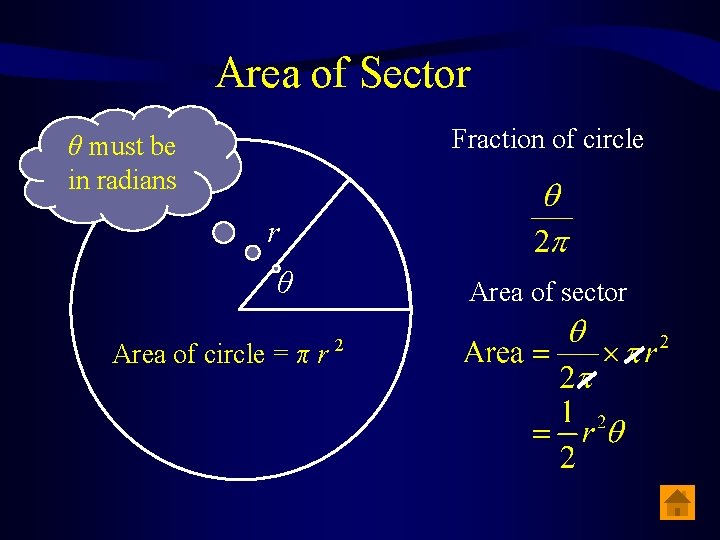
Area of Sector Fraction of circle θ must be in radians r θ Area of circle = π r 2 Area of sector

θ must be in radians r θ Page 9 of tables

Examples A circle has radius length 8 cm. An angle of 2· 5 radians is subtended by an arc. Find the length of the arc. l = rθ l = 2· 5 8 = 20 cm l 2· 5 8 cm

(i) Find the length of the minor arc PQ. (ii) Find the area of the minor sector OPQ. Q 1. Q 2. P 10 cm O 0· 8 rad Q l = rθ = 10(0· 8) = 8 cm P 12 cm O l = rθ Q

Q 3. The bend on a running track is a semi-circle of radius 100 metres. π A 20 m A runner, on the track, runs a distance of 20 metres on the bend. The angles through which the runner has run is A. Find to three significant figures, the measure of A in radians. l = rθ 100 20 = θ π π θ = 20 100 = 0· 6283. . = 0· 628 radians

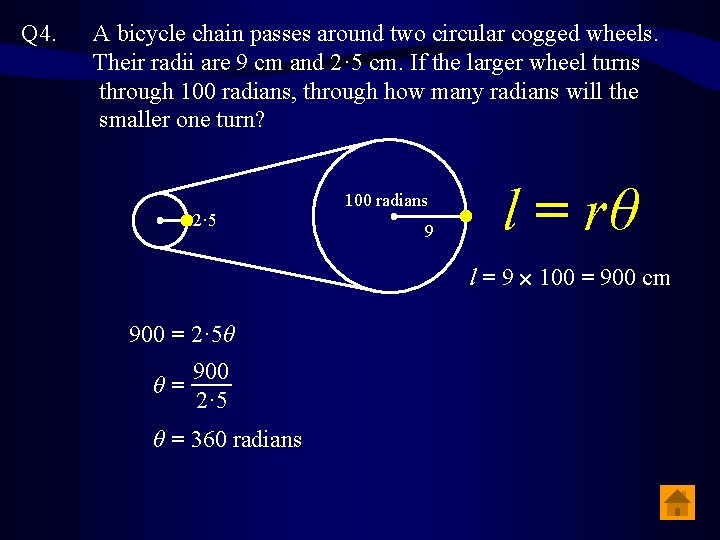
Q 4. A bicycle chain passes around two circular cogged wheels. Their radii are 9 cm and 2· 5 cm. If the larger wheel turns through 100 radians, through how many radians will the smaller one turn? 2· 5 100 radians 9 l = rθ l = 9 100 = 900 cm 900 = 2· 5θ 900 θ= 2· 5 θ = 360 radians

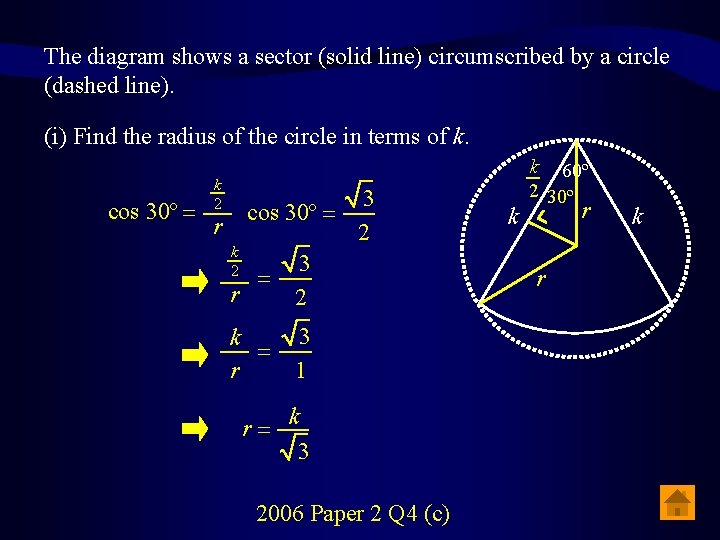
The diagram shows a sector (solid line) circumscribed by a circle (dashed line). (i) Find the radius of the circle in terms of k. cos 30º = k 2 3 cos 30º = r 2 k 3 2 = r 2 3 k = r 1 r= k 3 2006 Paper 2 Q 4 (c) k k 60º 2 30º r r k

The diagram shows a sector (solid line) circumscribed by a circle (dashed line). (ii) Show that the circle encloses an area which is double that of the sector. r= Area of circle = π r 2 æ k ö 2 =πç ÷ è 3ø k 3 Twice area of sector Area of sector 2006 Paper 2 Q 4 (c) 3 k r r k

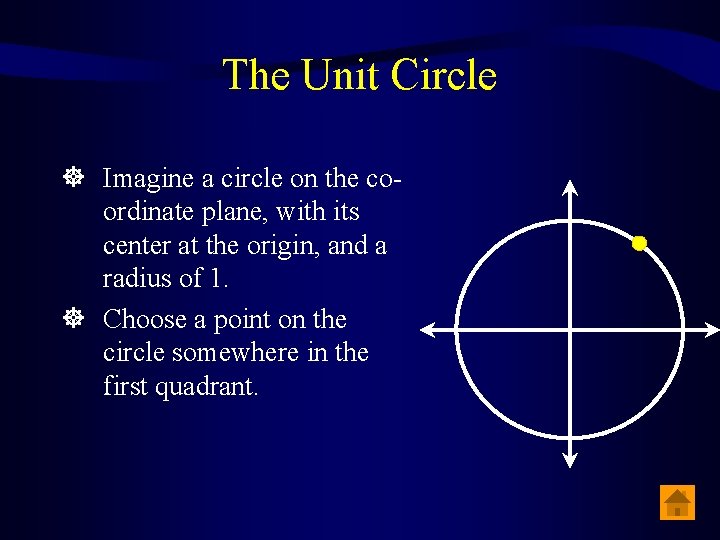
The Unit Circle Imagine a circle on the coordinate plane, with its center at the origin, and a radius of 1. Choose a point on the circle somewhere in the first quadrant.

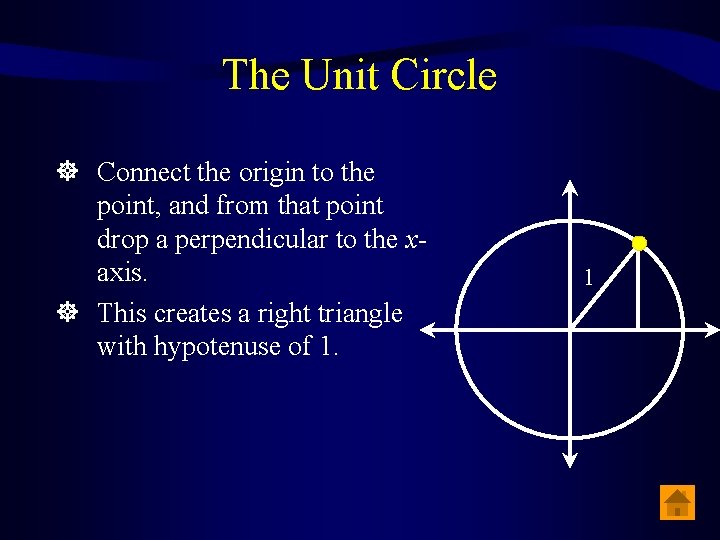
The Unit Circle Connect the origin to the point, and from that point drop a perpendicular to the xaxis. This creates a right triangle with hypotenuse of 1. 1

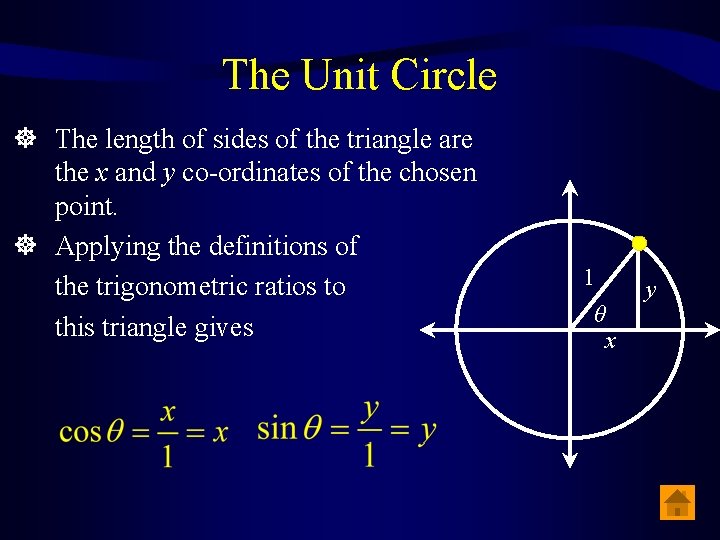
The Unit Circle The length of sides of the triangle are the x and y co-ordinates of the chosen point. Applying the definitions of the trigonometric ratios to this triangle gives 1 θ x y

The Unit Circle The co-ordinates of the chosen point are the cosine and sine of the angle . This provides a way to define functions sin and cos for all real numbers . The other trigonometric functions can be defined from these.

Trigonometric Functions cosecant cotan 1 θ x y

Around the Circle As that point moves around the unit circle into the second, third and fourth quadrants, the new definitions of the trigonometric functions still hold.

Reference Angles The angles whose terminal sides fall in the 2 nd, 3 rd, and 4 th quadrants will have values of sine, cosine and other trig functions which are identical (except for sign) to the values of angles in 1 st quadrant. The acute angle which produces the same values is called the reference angle.

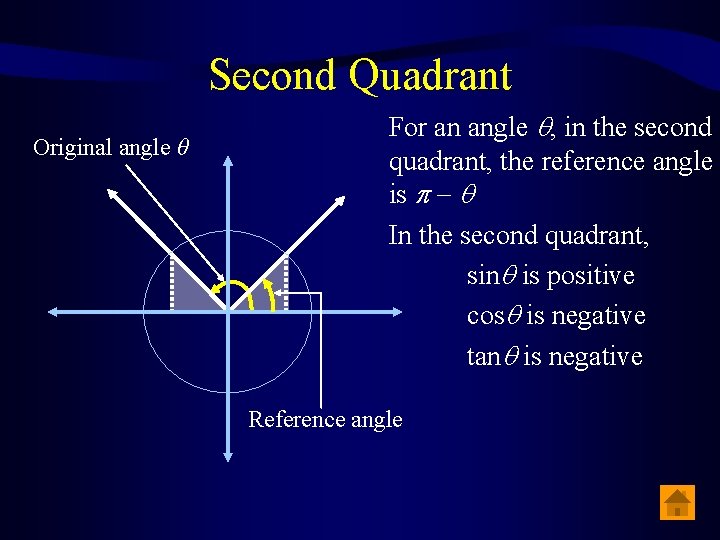
Second Quadrant Original angle θ For an angle , in the second quadrant, the reference angle is In the second quadrant, sin is positive cos is negative tan is negative Reference angle

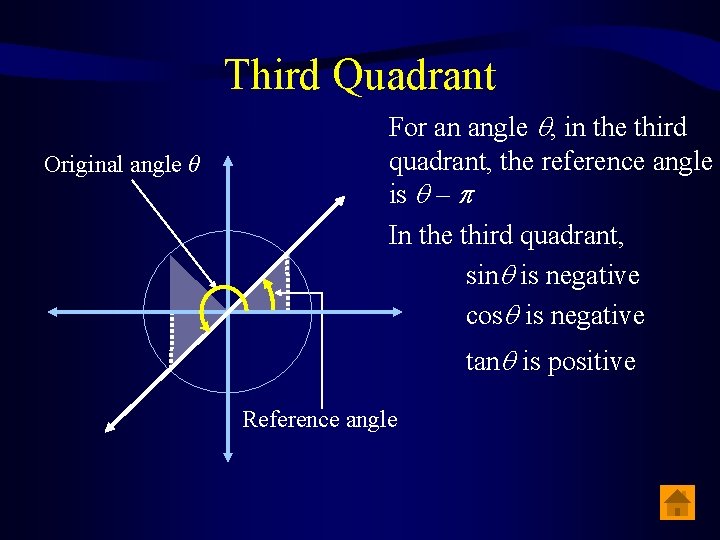
Third Quadrant Original angle θ For an angle , in the third quadrant, the reference angle is – In the third quadrant, sin is negative cos is negative tan is positive Reference angle

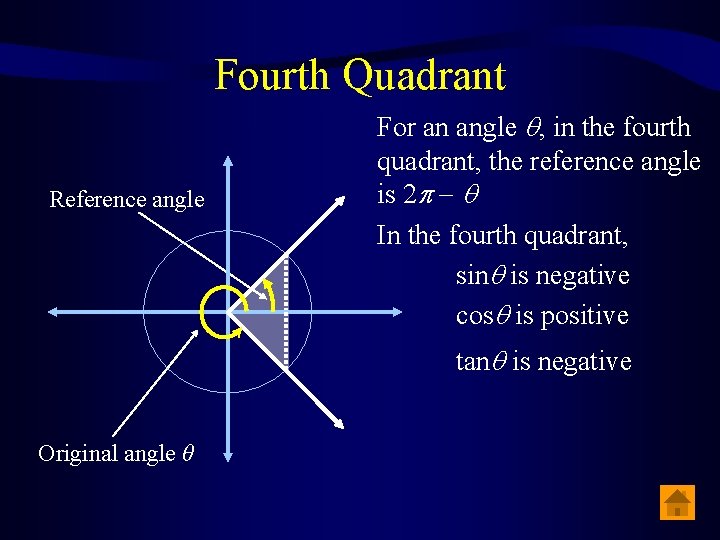
Fourth Quadrant Reference angle For an angle , in the fourth quadrant, the reference angle is 2 In the fourth quadrant, sin is negative cos is positive tan is negative Original angle θ

All Students Take Care Use the phrase “All Students Take Care” to remember the signs of the trigometric functions in the different quadrants. Take All Care S A T C C Students

Examples Find sin 240° in surd form. A T C C S – Draw the angle on the unit circle – In the 3 rd quadrant sine is negative – Find the angle to nearest x-axis 60º

Examples cosθ = – 0· 5. Find the two possible values of θ, where 0º ≤ θ ≤ 360°. cos. A = 0· 5 60º cos is negative in two quadrants 2 nd 180º – 60º 120º 3 rd 180º + 60º 240º S A T C

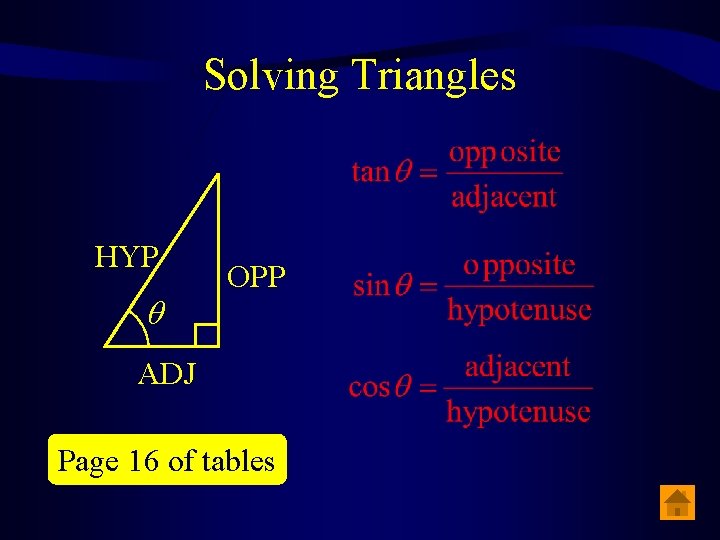
Solving Triangles HYP OPP ADJ Page 16 of tables

Trigonometric ratios in surd form 3 tan 60 º = 1 3 sin 60 º = 2 1 cos 60 º = 2 30º 2 3 60º 1 tan 30 º = 1 tan 45 º = 1 3 1 sin 45 º = sin 30 º = 2 3 cos 45 º = cos 30 º = 2 Page 13 of tables 45º 2 1 45º 1 Angles are given in radians and degrees π radians = 180º π π = 90º = 60º = 45º = 30º 2 3 4 6 1 2

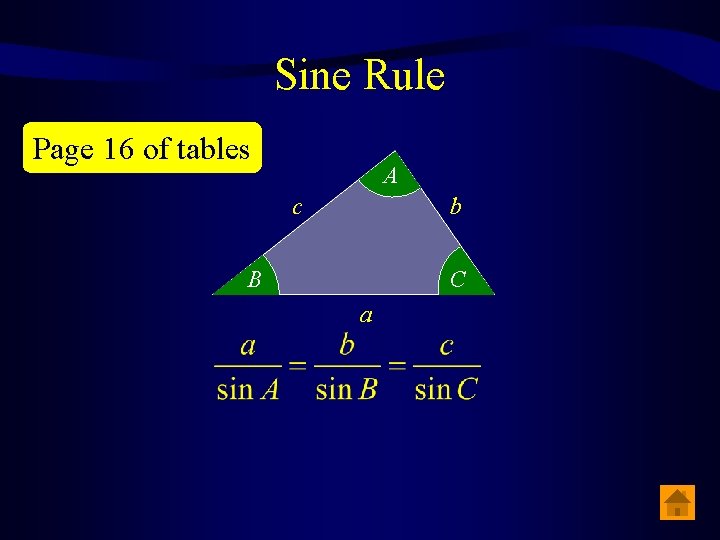
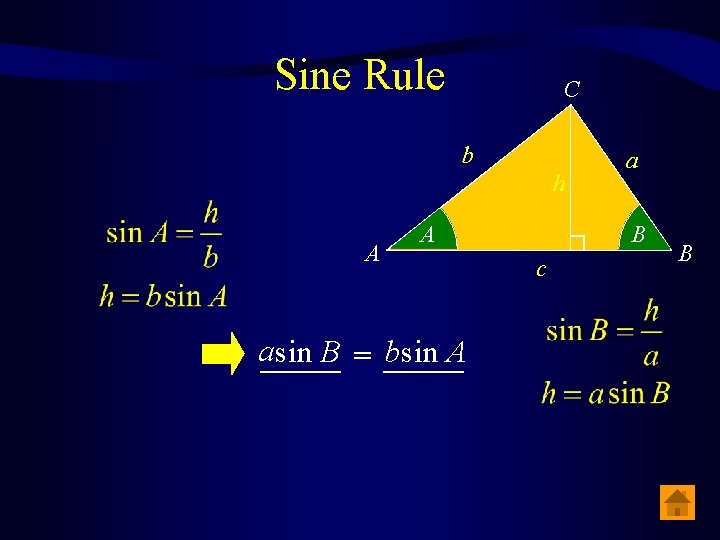
Sine Rule Page 16 of tables A c b B C a

Sine Rule C b h A A a_____ b sin A sin B = _____ a B c B

Two surveyors want to find the height of an electricity pylon. There is a fence around the pylon that they cannot cross for safety reasons. The ground is inclined at an angle. They have a clinometer and a 100 metre tape measure. They have already used the clinometer to determine that the ground is inclined at 10° to the horizontal. (a) Explain how they could find the height of the pylon. Your answer should be illustrated on the diagram below. Show the points where you think they should take measurements, and write down clearly what measurements they should take. 10° 2010 SEC Sample Paper 2 Q 8

Two surveyors want find the from height of points an electricity Measure the angle ofto elevation two A pylon. There is a fence around that they and B and subtract 10° to get α the andpylon β as shown. cannot cross for safetyfrom reasons. ground inclined Measure the distance A to The B (less than is 100 m) at an angle. They have a clinometer and a 100 metre tape measure. They have already used the clinometer to determine that the ground is inclined at 10° to the horizontal. (a) Explain how they could find the height of the pylon. Your answer should be illustrated on the diagram below. Show the points where you think they should take measurements, and write down clearly what β–α measurements they should take. 180° – β β A α 10° B 2010 SEC Sample Paper 2 Q 8 D C 20

a bheight _____ c _____ Two surveyors want to find=the Sine Rule: = of an electricity sin around A sinthat C they pylon. There is a fence the. Bpylon cannot cross for |safety ground is inclined 30 The DB | reasons. ______ __ at an angle. They have a= clinometer and 15 a 100 metre sin 40º sin 15º tape measure. They have already used the clinometer = 74· 506. . to determine that the ground Multiply both sides is byinclined sin 40 at 10° to the = 74· 5 m horizontal. (b) Write down possible values for the D measurements taken, and use them to show to find the height of the pylon. (That is, find the height of the pylon using your measurements, and showing your work. ) 15° β–α Let α = 40° β 55° 180° – β 30 m Let β = 55° 40° α C A 10° B Let | AB| = 30 m 2010 SEC Sample Paper 2 Q 8

a bheight _____ c _____ Two surveyors want to find=the Sine Rule: = of an electricity sin around A sinthat C they pylon. There is a fence the. Bpylon cannot cross for |safety ground is inclined 74· 5 The DC | reasons. ______ __ at an angle. They have a= clinometer and a 100 metre sin 55º sin 100º tape measure. They have already used the clinometer = 61· 968. . to determine that the ground Multiply both sides is byinclined sin 55 at 10° to the = 62 m horizontal. (b) Write down possible values for the measurements taken, and use them to show to find the height of the pylon. (That is, find the height of the pylon using your measurements, and showing your work. ) 15° Let α = 40° Let β = 55° A 40° 30 m 10° B Let | AB| = 30 m 2010 SEC Sample Paper 2 Q 8 55° D 90° 100° + 10° C

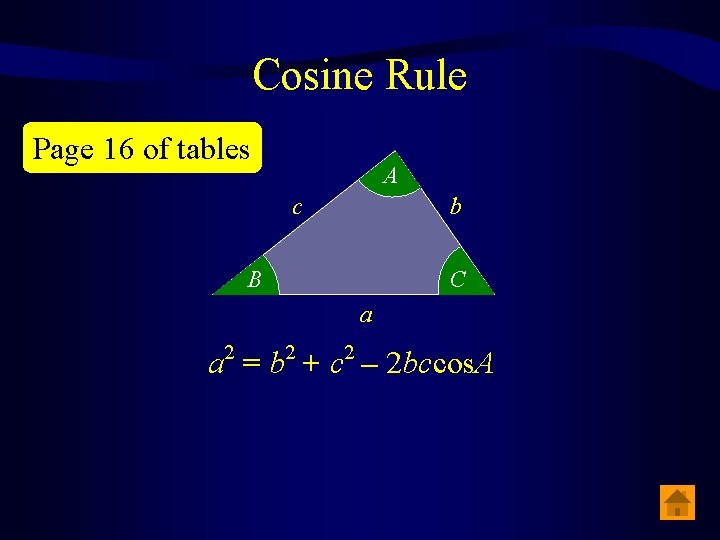
Cosine Rule Page 16 of tables A c b B C a 2 2 2 a = b + c – 2 bccos. A

Cosine Rule b By Pythagoras’ Theorem 2 2 A a 2 = c 2 – 2 cx + x 2 + h 2 a 2 = b 2 + c 2 – 2 cx 2 2 2 a = b + c – 2 bccos. A a h 2 a = (c – x) + h C A x c c–x b 2 = x 2 + h 2 B

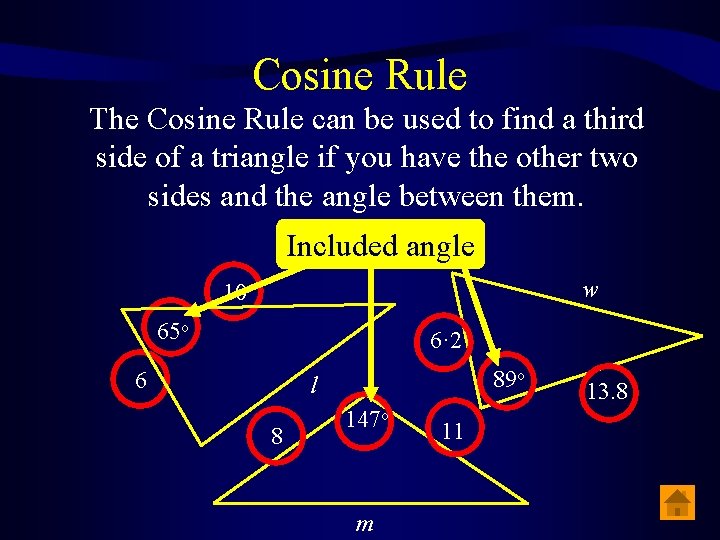
Cosine Rule The Cosine Rule can be used to find a third side of a triangle if you have the other two sides and the angle between them. Included angle w 10 65 o 6· 2 6 89 o l 8 147 o m 11 13. 8

Examples Find the unknown side in the triangle below: l 5 m 43 o 12 m Identify sides a, b, c and angle Ao Write down the Cosine Rule a = l b = 5 c = 12 A = 43º 2 2 2 a = b + c – 2 bccos. A 2 2 2 Substitute values and find a 2 Take square root of both sides a = 5 + 12 – 2 5 12 cos 43 o a 2 = 25 + 144 – 120(0· 731) a 2 = 81· 28 a = 9· 02 m

Examples Find the unknown side in the triangle below: 12· 2 cm 137 o 17· 5 cm a=? b = 12· 2 c = 17· 5 a 2 = b 2 + c 2 – 2 bccos. A A = 137º a 2 = 12· 22 + 17· 52 – ( 2 12· 2 17· 5 cos 137 o ) a 2 = 148· 84 + 306· 25 – ( 427 – 0· 731 ) a 2 = 455· 09 + 312· 137 a 2 = 767· 227 a = 27· 7 cm

Examples Find the two possible values for the unknown side. a=6 x 6 b = 10 20 o 10 a 2 = b 2 + c 2 – 2 bccos. A 62 = 102 + x 2 – (2 10 x cos 20 o) 36 = 100 + x 2 – 20 x( 0· 9397) 0 = x 2 – 18· 79 x + 64 c=x A = 20º

Examples Find the two possible values for the unknown side. a = 16 x 6 2 0 = x – 18· 79 x + 64 10 b = – 18· 79 10 20 o c = 64 x A = 20º

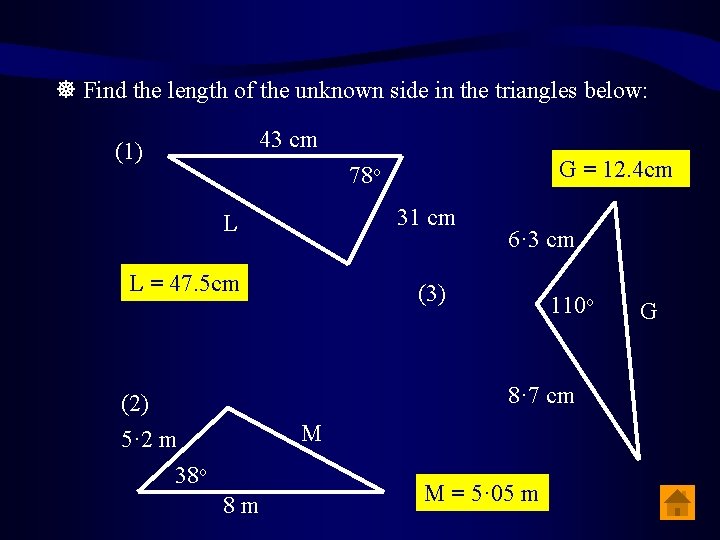
Find the length of the unknown side in the triangles below: 43 cm (1) G = 12. 4 cm 78 o 31 cm L L = 47. 5 cm 6· 3 cm (3) 110 o 8· 7 cm (2) M 5· 2 m 38 o 8 m M = 5· 05 m G

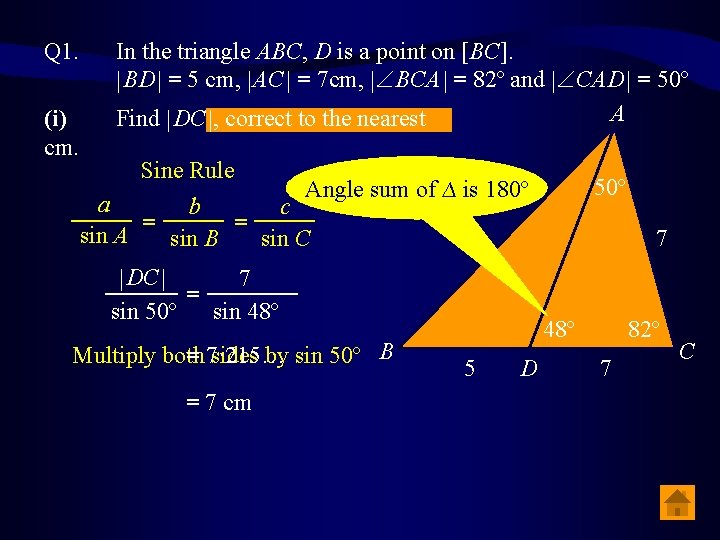
Q 1. . (i) cm. In the triangle ABC, D is a point on [BC]. BD = 5 cm, AC = 7 cm, BCA = 82º and CAD = 50º A Find DC , correct to the nearest Sine Rule 50º Angle sum of ∆ is 180º a b c _____ = = sin A sin B sin C DC 7 __ ______ = sin 50º sin 48º Multiply both sides by sin 50º B = 7· 215… = 7 cm 7 48º 5 D 82º 7 C
![Q 1 ii In the triangle ABC D is a point on BC Q 1. . (ii) In the triangle ABC, D is a point on [BC].](https://slidetodoc.com/presentation_image_h2/a60b235fa4d113d8a7b1bdbe44e0ece1/image-46.jpg)
Q 1. . (ii) In the triangle ABC, D is a point on [BC]. BD = 5 cm, AC = 7 cm, BCA = 82º and CAD = 50º A Find AB , correct to the nearest cm. Cosine Rule: 50º a 2 = b 2 + c 2 – 2 bc cos. A 2 2 7 2 AB = 12 + 7 – 2(12)(7)cos 82º = 144 + 49 – 168 cos 82º = 169· 6189… B 82º 5 D 7 AB = 169· 6189 = 13· 02… = 13 cm + = 12 C

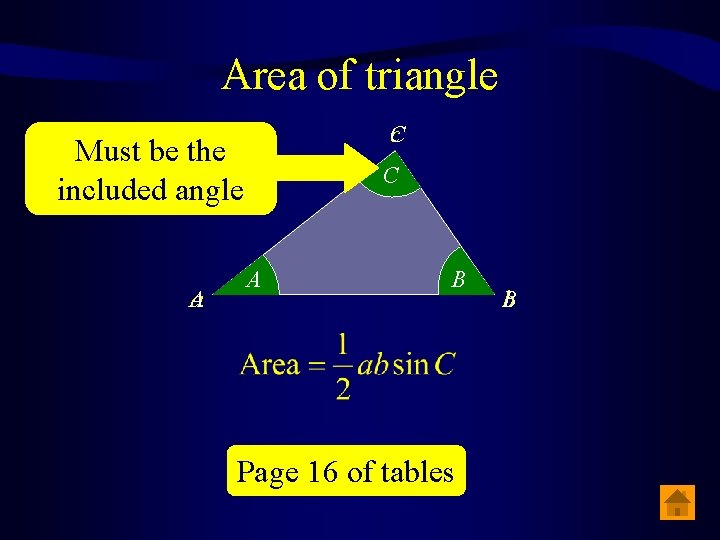
Area of triangle C c Must be the included angle A a C A B Page 16 of tables B b

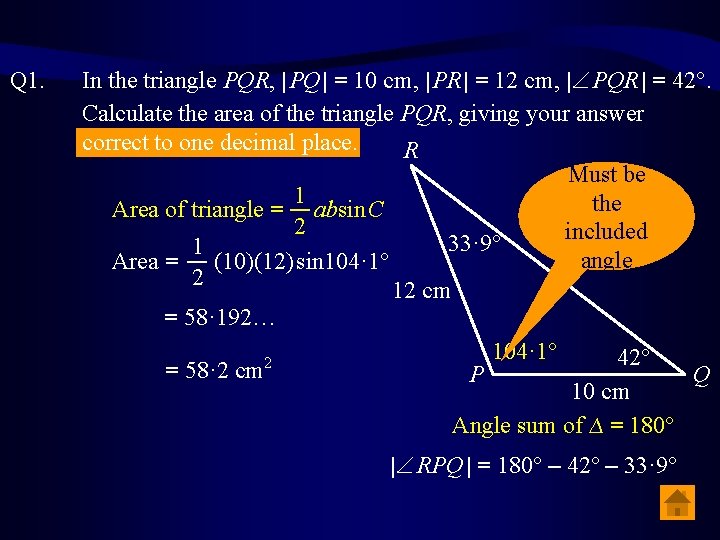
Q 1. In the triangle PQR, | PQ | = 10 cm, | PR | = 12 cm, | PQR | = 42. Calculate the area of the triangle PQR, giving your answer correct to one decimal place. R Must be 1 the Area of triangle = absin C 2 included 33· 9 1 angle Area = (10)(12) sin 104· 1 2 12 cm = 58· 192… 104· 1 42 2 = 58· 2 cm P Q 10 cm Angle sum of ∆ = 180 | RPQ | = 180 – 42 – 33· 9

Identities involving Cosine Rule Using the usual notation for a triangle, prove that c(bcos. A – acos. B) = b 2 – a 2

Identities involving Cosine Rule Using the usual notation for a triangle, prove that c(bcos. A – acos. B) = b 2 – a 2

2 2 cos θ + sin θ = 1 By Pythagoras’ Theorem x 2 + y 2 = r 2 Divide both sides by r (x, y) r θ x y

3 D Trigonometry
![S P Q and R are points on level ground SR is a vertical S P, Q and R are points on level ground, [SR] is a vertical](https://slidetodoc.com/presentation_image_h2/a60b235fa4d113d8a7b1bdbe44e0ece1/image-53.jpg)
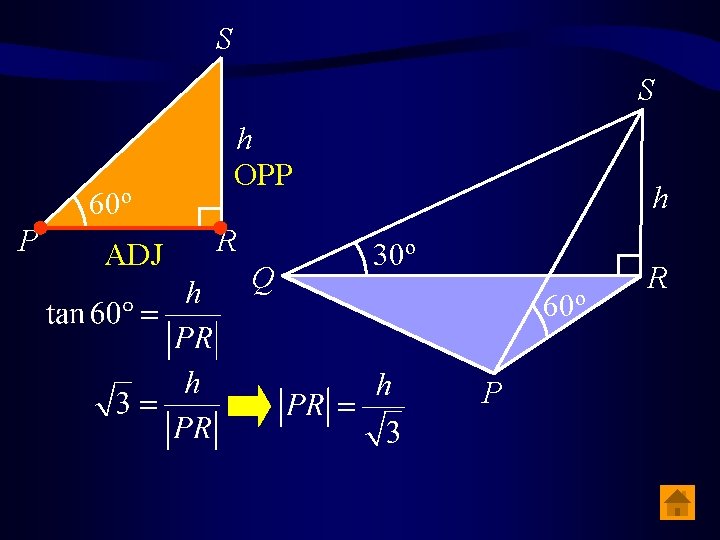
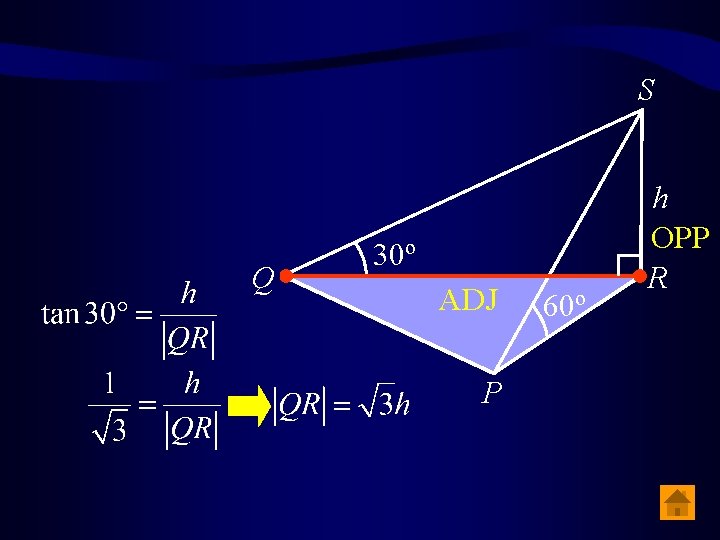
S P, Q and R are points on level ground, [SR] is a vertical flagpole of height h. The angles of elevation of the top of the flagpole from P and Q are α and β, respectively. Q (i) h. h β 30º If | α | = 60º and | β | = 30º, express | PR | and | QR | in terms of 60º α P R

S S 60º P ADJ h OPP R Q h 30º 60º P R

S Q 30º ADJ P 60º h OPP R

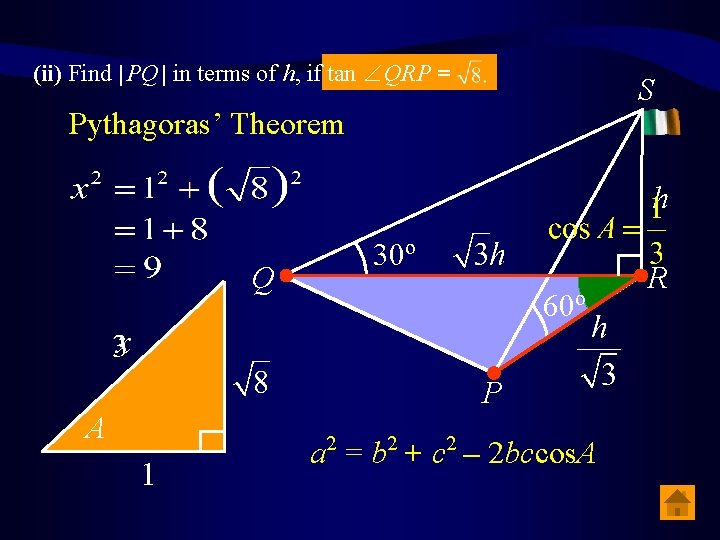
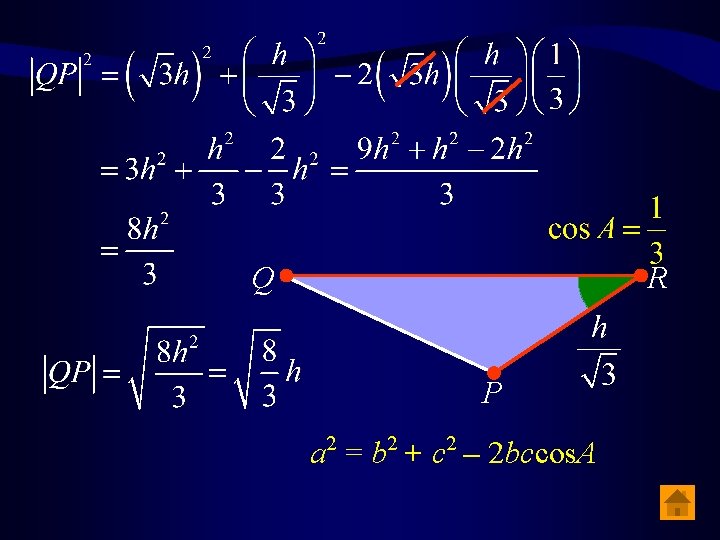
(ii) Find | PQ | in terms of h, if tan QRP = S Pythagoras’ Theorem h Q A 30º 60º P a 2 = b 2 + c 2 – 2 bccos. A R

Q R P a 2 = b 2 + c 2 – 2 bccos. A

The great pyramid at Giza in Egypt has a square base and four triangular faces. The base of the pyramid is of side 230 metres and the pyramid is 146 metres high. slanted edge The top of the pyramid is directly above the centre of the base. (i) Calculate the length of one of the slanted edges, correct to the nearest metre. Pythagoras’ theorem 146 162· 6 x x = 105800 2 x = 325· 269. . = 162· 6 2 2006 Paper 2 Q 5 (b) 162· 6 230 m

The great pyramid at Giza in Egypt has a square base and four triangular faces. The base of the pyramid is of side 230 metres and the pyramid is 146 metres high. slanted edge The top of the pyramid is directly above the centre of the base. (i) Calculate the length of one of the slanted edges, correct to the nearest metre. Pythagoras’ theorem 146 162· 6 l l = 47754· 76 2 l = 218· 528. . = 219 m 2006 Paper 2 Q 5 (b) 162· 6 m 146 m

(ii) Calculate, correct to two significant numbers, the total area of the four triangular faces of the pyramid (assuming they are smooth flat surfaces) Pythagoras’ theorem slanted edge 219 m h 2 = 34736 = 186· 375. . = 186· 4 m h 115 m 230 m 1 Area of triangle = base × height 2 1 = (230)(186· 4) 2 2 = 21436 m 2006 Paper 2 Q 5 (b)

(ii) Calculate, correct to two significant numbers, the total area of the four triangular faces of the pyramid (assuming they are smooth flat surfaces) Pythagoras’ theorem slanted edge 219 m h = 34736 = 186· 375. . = 186· 4 m 115 m Total area = 21436 4 = 85744 m 2 = 86000 m 2 2006 Paper 2 Q 5 (b) h

S R h θ P Q 3 x T 2θ x P R h θ 3 x QRST is a vertical wall of height h on level ground. P is a point on the ground in front of the wall. The angles of elevation of R from P is θ and the angle of elevation of S from P is 2θ. | PQ | = 3| PT |. Find θ. 2005 Paper 2 Q 5 (c) Q

S S P h 2θ x T P R h θ 3 x QRST is a vertical wall of height h on level ground. P is a point on the ground in front of the wall. The angles of elevation of R from P is θ and the angle of elevation of S from P is 2θ. | PQ | = 3| PT |. Find θ. 2005 Paper 2 Q 5 (c) Q

S 3 xtan θ = xtan 2θ T 2θ x P R h θ 3 x Let t = tan θ 2005 Paper 2 Q 5 (c) Q

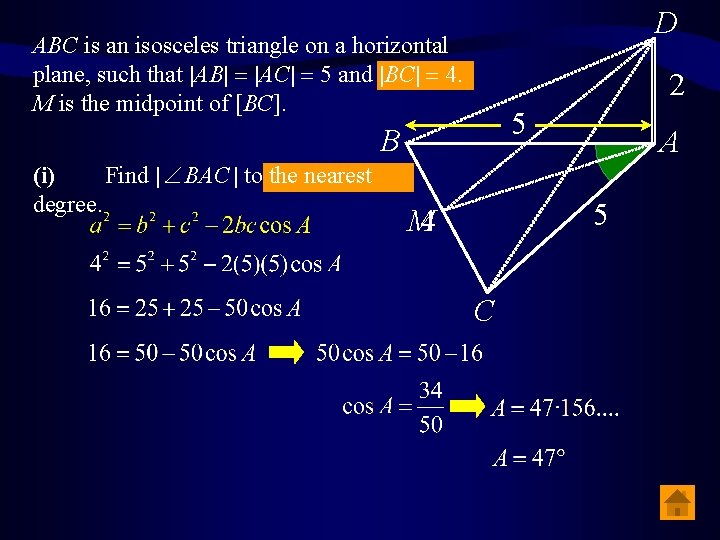
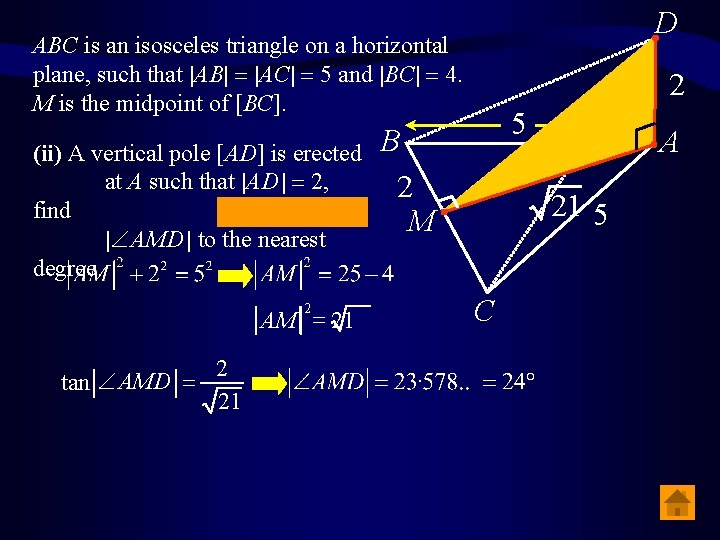
D ABC is an isosceles triangle on a horizontal plane, such that |AB| = |AC| = 5 and |BC| = 4. M is the midpoint of [BC]. 2 5 B (i) Find | BAC | to the nearest degree. A 5 M 4 C

D ABC is an isosceles triangle on a horizontal plane, such that |AB| = |AC| = 5 and |BC| = 4. M is the midpoint of [BC]. (ii) A vertical pole [AD] is erected at A such that |AD | = 2, find | AMD | to the nearest degree. 2 AM = 21 tan AMD = 2 21 2 5 B 2 M A 21 5 C

Trigonometric Identities An identity is an equation which is true for all values of the variable. There are many trig identities that are useful in changing the appearance of an expression. The most important ones should be committed to memory.

Trigonometric Identities Reciprocal Identities Quotient Identities

Trigonometric Identities Pythagorean Identities The fundamental Pythagorean identity Divide by sin 2 x 2 Divide by cos x

Solving Trig Equations To solve trigonometric equations: If there is more than one trigonometric function, use identities to simplify Let a variable represent the remaining function Solve the equation for this new variable Reinsert the trigonometric function Determine the argument which will produce the desired value

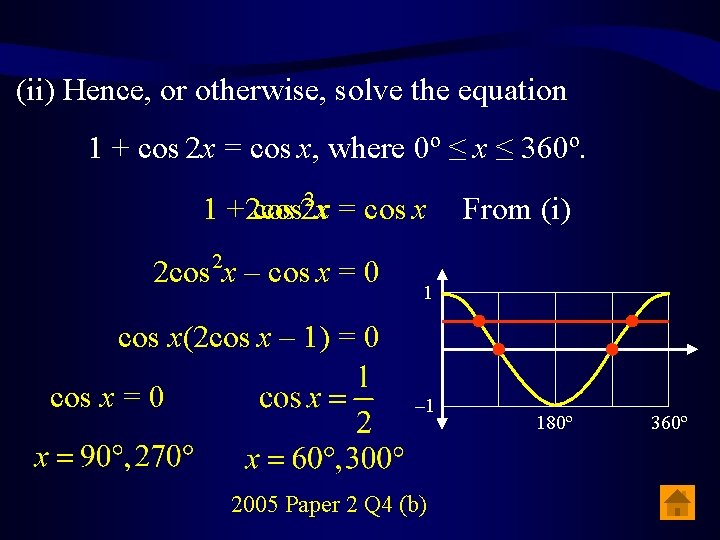
2 2 (i) Using cos 2 A = cos A – sin A, or otherwise, prove 1 2 cos A = (1 + cos 2 A). 2 cos 2 A = cos 2 A – (1 sin– 2 Acos 2 A) 2 2 cos 2 A = cos A – 1 + cos A 2 1 + cos 2 A = 2 cos A – 1 1 cos A = (1 + cos 2 A) 2 2 2005 Paper 2 Q 4 (b)

(ii) Hence, or otherwise, solve the equation 1 + cos 2 x = cos x, where 0º ≤ x ≤ 360º. 2 1 +2 cos 2 x x = cos x 2 cos 2 x – cos x = 0 From (i) 1 cos x(2 cos x – 1) = 0 cos x = 0 – 1 2005 Paper 2 Q 4 (b) 180º 360º

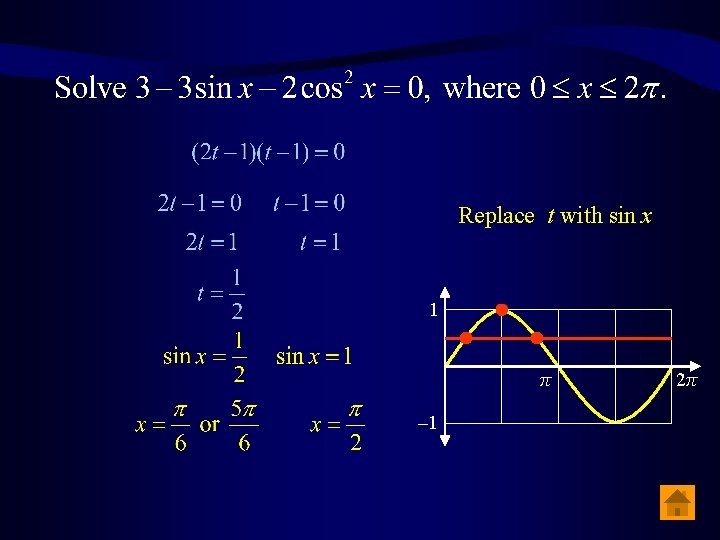
Expand Collect like terms Rearrange Factorise

Replace t with sin x 1 π – 1 2π

Trigonometric Formulas Page 13 of tables

Trigonometric Formulas

Replace B with – B
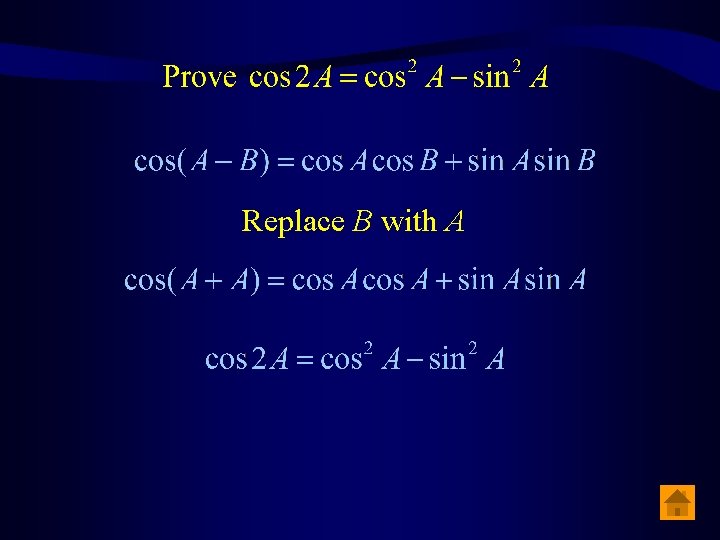
Replace B with A

Replace A with –A

Graphing Trig Functions

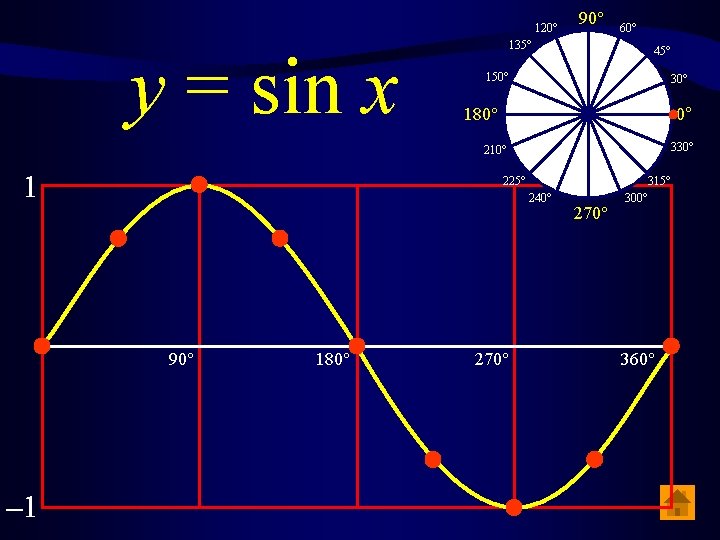
120° y = sin x 90° 135° 60° 45° 150° 30° 180° 0° 330° 210° 1 225° 240° 90° – 1 180° 270° 315° 300° 360°

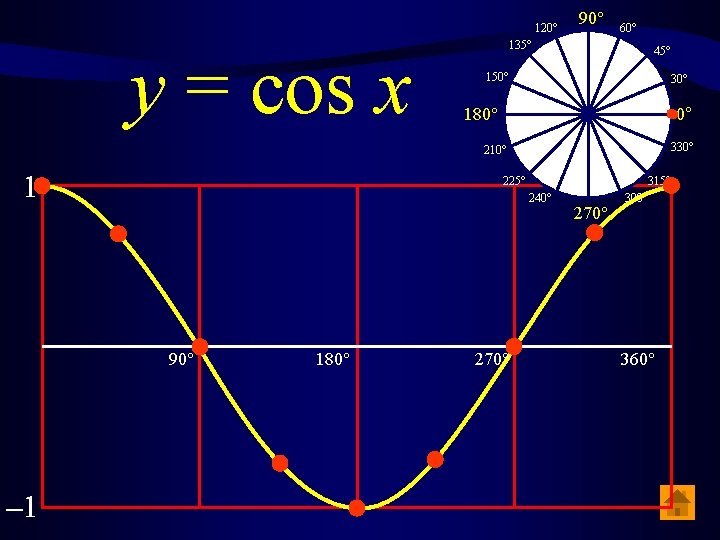
120° y = cos x 90° 135° 60° 45° 150° 30° 180° 0° 330° 210° 1 225° 240° 90° – 1 180° 270° 315° 300° 360°

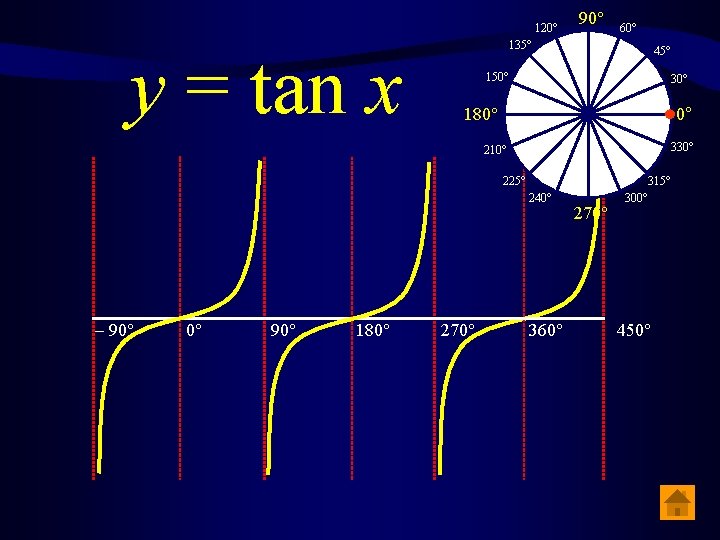
120° y = tan x 90° 60° 135° 45° 150° 30° 180° 0° 330° 210° 225° 240° – 90° 0° 90° 180° 270° 360° 270° 315° 300° 450°

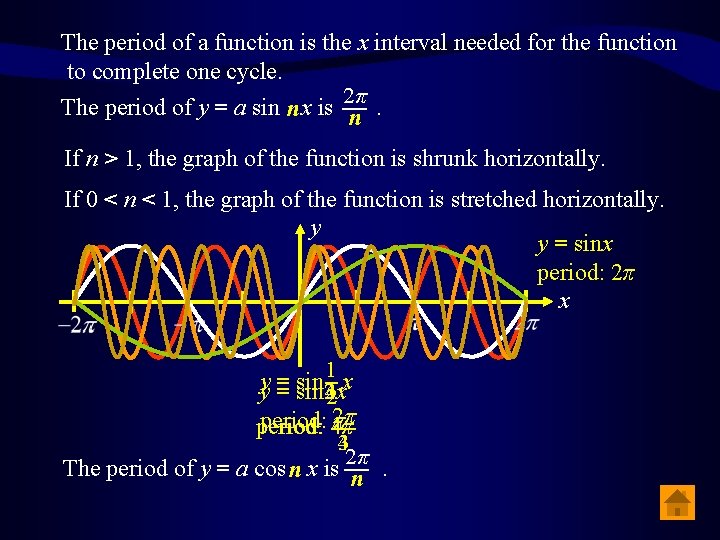
The period of a function is the x interval needed for the function to complete one cycle. 2π The period of y = a sin n x is –– n. If n > 1, the graph of the function is shrunk horizontally. If 0 < n < 1, the graph of the function is stretched horizontally. y y = sinx period: 2π x 1 x yy = = sin 4 x sin – sin 3 x sin 2 x 2 2π period: 4π π period: –– 43 2π The period of y = a cos n x is –– n.

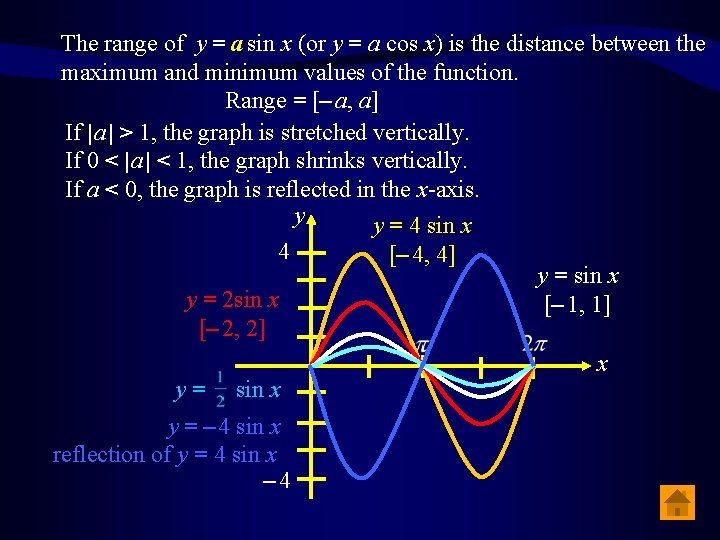
The range of y = a sin x (or y = a cos x) is the distance between the maximum and minimum values of the function. Range = [– a, a] If | a | > 1, the graph is stretched vertically. If 0 < | a | < 1, the graph shrinks vertically. If a < 0, the graph is reflected in the x-axis. y y = 4 sin x 4 y = 2 sin x [– 2, 2] y= sin x y = – 4 sin x reflection of y = 4 sin x – 4 [– 4, 4] y = sin x [– 1, 1] x

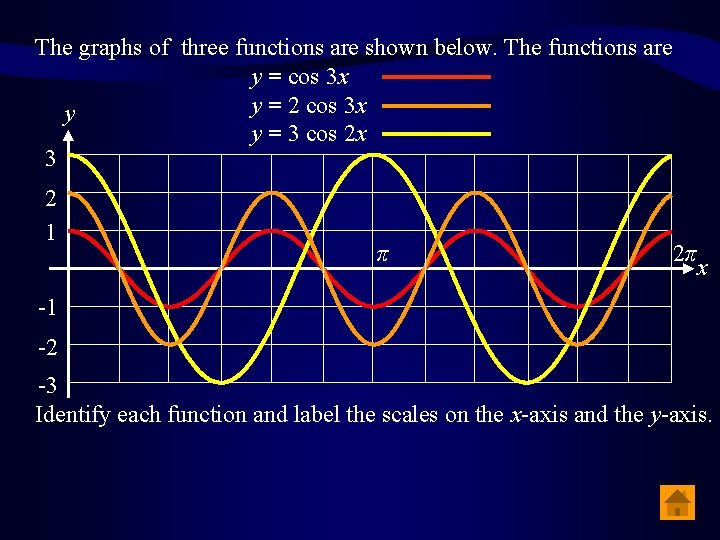
The graphs of three functions are shown below. The functions are y = cos 3 x y = 2 cos 3 x y y = 3 cos 2 x 3 2 1 π 2π x -1 -2 -3 Identify each function and label the scales on the x-axis and the y-axis.

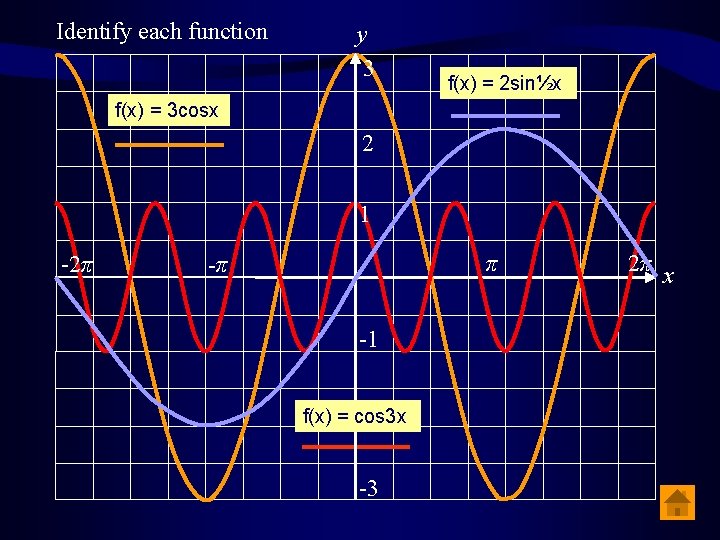
Identify each function y 3 f(x) = 2 sin½x f(x) = 3 cosx 2 1 -2π π -π -1 f(x) = cos 3 x -2 -3 2π x

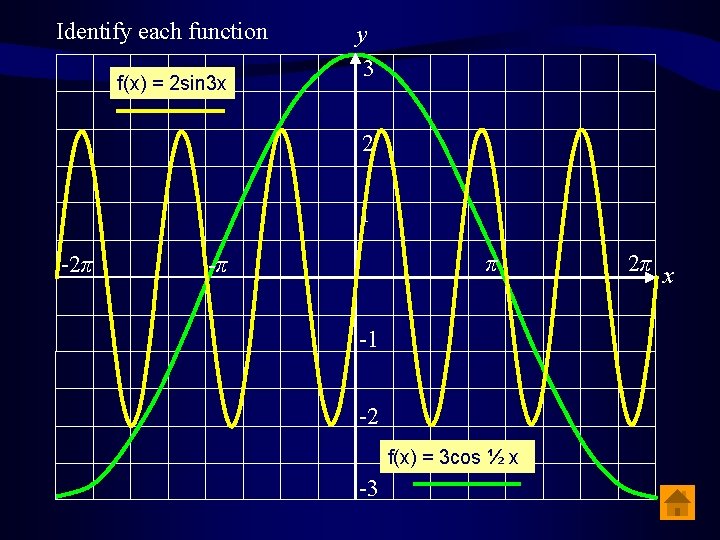
Identify each function f(x) = 2 sin 3 x y 3 2 1 -2π π -π -1 -2 f(x) = 3 cos ½ x -3 2π x

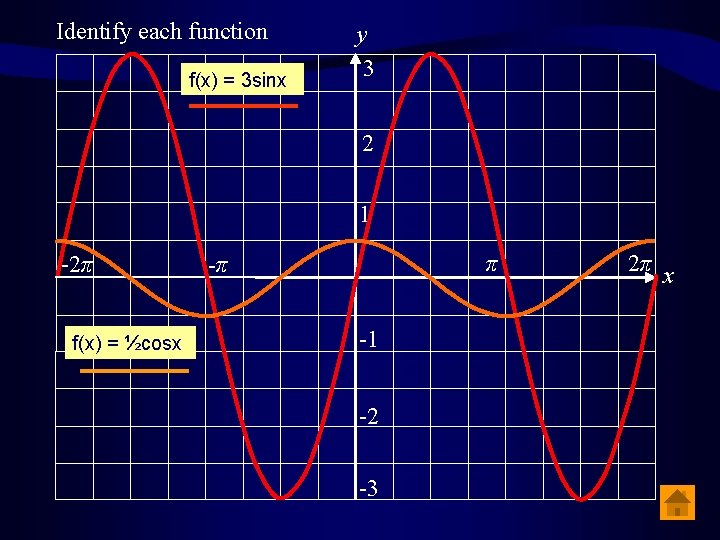
Identify each function f(x) = 3 sinx y 3 2 1 -2π f(x) = ½cosx π -π -1 -2 -3 2π x

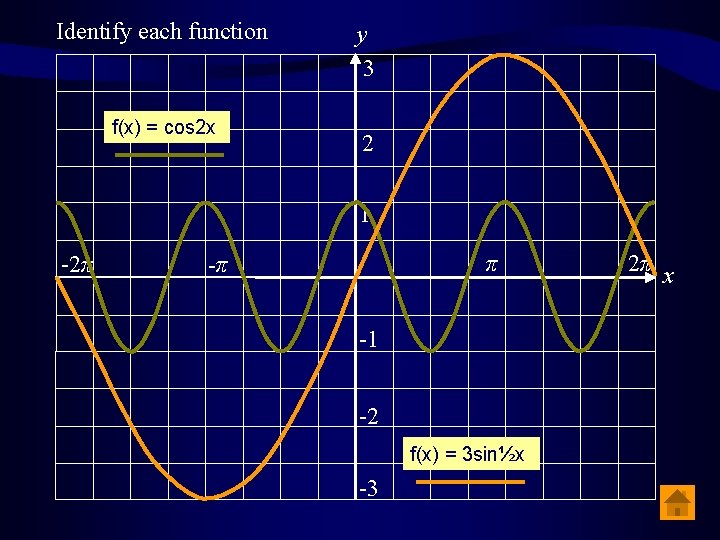
Identify each function f(x) = cos 2 x y 3 2 1 -2π π -π -1 -2 f(x) = 3 sin½x -3 2π x
 Area of a sector formula radians
Area of a sector formula radians Additional topics in trigonometry
Additional topics in trigonometry What is the ratio of the length of to the length of ?
What is the ratio of the length of to the length of ? Convert each degree measure into radians
Convert each degree measure into radians Rad/s
Rad/s Convert degrees to radians worksheet doc
Convert degrees to radians worksheet doc Sector area radians
Sector area radians Dr frost radians
Dr frost radians Dms to radians
Dms to radians Satc quadrants
Satc quadrants Radians quadrants
Radians quadrants 8-2 special right triangles answer key
8-2 special right triangles answer key Convert from degrees to radians 225 degrees
Convert from degrees to radians 225 degrees Area of a sector formula radians
Area of a sector formula radians Unit circle radians
Unit circle radians Area of a sector radians
Area of a sector radians Ways to measure angles
Ways to measure angles 54 degrees to radians
54 degrees to radians Reference angle of 315
Reference angle of 315 Radian measure
Radian measure Convert each degree measure into radians
Convert each degree measure into radians Arc area radians
Arc area radians What is the value of 208º in radians?
What is the value of 208º in radians? Doc duane adult topics
Doc duane adult topics Prerequisites for health education
Prerequisites for health education Efl research topics
Efl research topics What is a newspaper
What is a newspaper Bin yao
Bin yao Cryptography topics crossword
Cryptography topics crossword Persuasive speech structures
Persuasive speech structures Email writing topics
Email writing topics Dialogue ki meaning
Dialogue ki meaning Arduino uno anatomy
Arduino uno anatomy Winter driving safety topics
Winter driving safety topics Sf 86 eqip
Sf 86 eqip Topics to be discussed
Topics to be discussed Define smaw
Define smaw Organizational communication topics
Organizational communication topics Computer organization topics
Computer organization topics Pollution topics
Pollution topics It management project topics
It management project topics Mlk diamante poem
Mlk diamante poem Black friday essay
Black friday essay Skill 15 listen for untrue conditions
Skill 15 listen for untrue conditions Opinion paragraph writing
Opinion paragraph writing Formulating and clarifying the research topic
Formulating and clarifying the research topic Tuning out dull topics
Tuning out dull topics Theme of death in the great gatsby chapter 4
Theme of death in the great gatsby chapter 4 Forklift safety meeting topics
Forklift safety meeting topics Drawing chapter 1
Drawing chapter 1 Peel example paragraph
Peel example paragraph Emphatic adjective
Emphatic adjective Hobby conversation
Hobby conversation Hot topics in leadership
Hot topics in leadership Special investigative topics 3232 quizlet
Special investigative topics 3232 quizlet Business economics topics
Business economics topics Advanced topics in angular
Advanced topics in angular Security meeting topics
Security meeting topics Body sentence in a paragraph
Body sentence in a paragraph Spre essay
Spre essay Modern studies assignment topics
Modern studies assignment topics Management topics for project
Management topics for project Software engineering important topics
Software engineering important topics Software architecture topics
Software architecture topics Special topics in software engineering
Special topics in software engineering Study circle topics
Study circle topics Customer service discussion topics
Customer service discussion topics Just a minute game topics
Just a minute game topics April safety topics
April safety topics Persuade reported speech
Persuade reported speech Blank for spectrophotometer
Blank for spectrophotometer Patty farris
Patty farris Leaflet letter writing
Leaflet letter writing Solo talk topics
Solo talk topics Business ethics presentation
Business ethics presentation Demonstration speech ideas
Demonstration speech ideas Letter writing format
Letter writing format Safety topics for august
Safety topics for august Engineering meeting topics
Engineering meeting topics How to write an empathy essay
How to write an empathy essay Division and classification essay
Division and classification essay Definition of an essay
Definition of an essay The apprentice pharmacist
The apprentice pharmacist Power point presentation topic in hindi
Power point presentation topic in hindi International marketing topics
International marketing topics 9th grade essay examples
9th grade essay examples Iimarch briefing example
Iimarch briefing example For women
For women Pde project topics
Pde project topics Themes in the catcher in the rye
Themes in the catcher in the rye Types of maps in maths lit
Types of maps in maths lit