Trigonometry Radian Measure Length of Arc Area of

Trigonometry Radian Measure Length of Arc Area of Sector

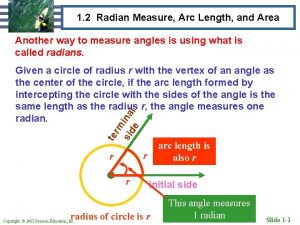
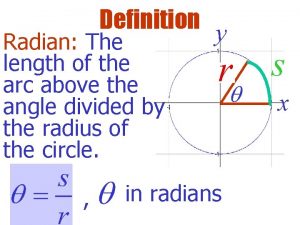
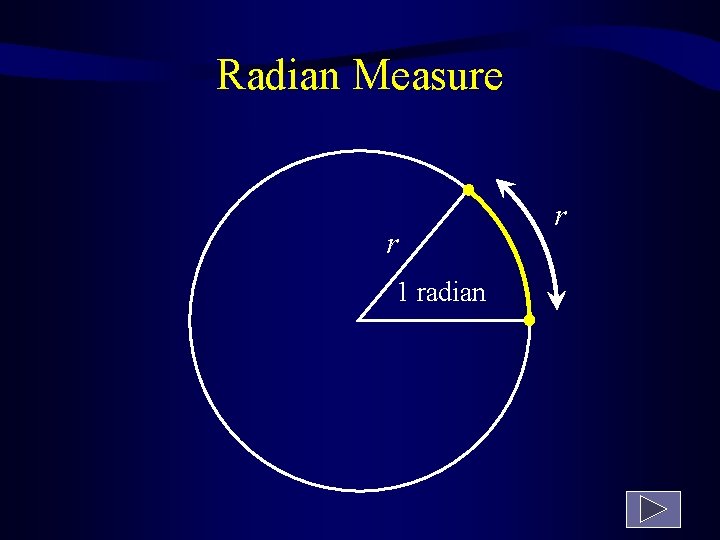
Radian Measure To talk about trigonometric functions, it is helpful to move to a different system of angle measure, called radian measure. A radian is the measure of a central angle whose minor arc is equal in length to the radius of the circle. There are 2 or approximately 6. 28318, radians in a complete circle. Thus, one radian is about 57. 296 angular degrees.

Radian Measure r 1 radian r

Radian Measure There are 2π radians in a full rotation – once around the circle There are 360° in a full rotation 2π = 360° π = 180° To convert from degrees to radians or radians to degrees, use the proportion degrees radians = 180 o

Examples Find the degree measure equivalent of 3π radians. 4 3π 3 180 = 4 4 = 135° Find the radian measure equivalent of 210°. 180° = π π 1° = 180 210π 7π 210° = = 180 6

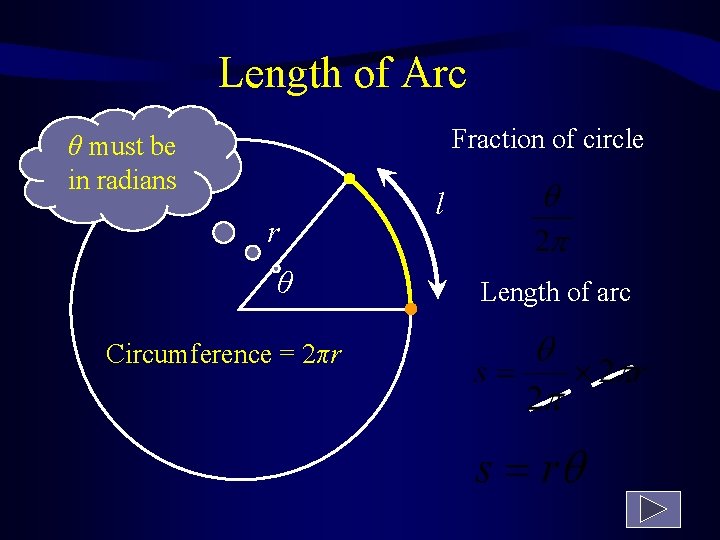
Length of Arc Fraction of circle θ must be in radians r θ Circumference = 2πr l Length of arc

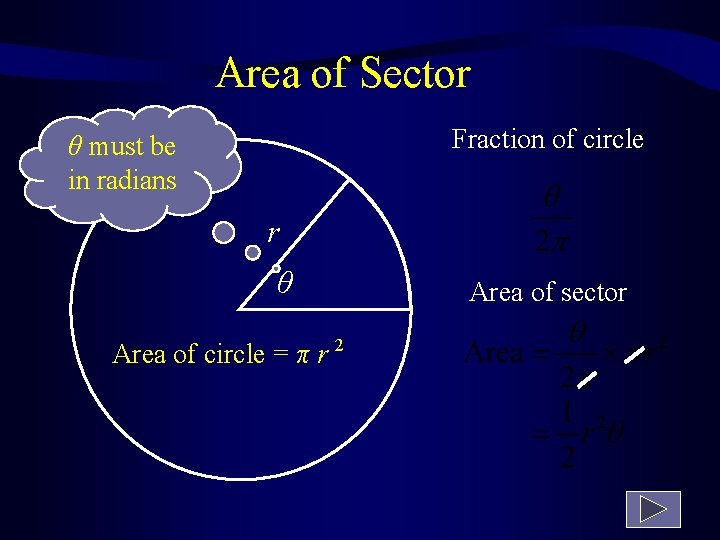
Area of Sector Fraction of circle θ must be in radians r θ Area of circle = π r 2 Area of sector

θ must be in radians r θ

Examples A circle has radius length 8 cm. An angle of 2. 5 radians is subtended by an arc. Find the length of the arc. s = rθ s = 2· 5 8 = 20 cm l 2· 5 8 cm

(i) Find the length of the minor arc pq. (ii) Find the area of the minor sector opq. Q 1. Q 2. p 10 cm o 0· 8 rad q s = rθ = 10(0· 8) = 8 cm p 12 cm o s = rθ q

Q 3. The bend on a running track is a semi-circle of radius 100 metres. π A 20 m A runner, on the track, runs a distance of 20 metres on the bend. The angles through which the runner has run is A. Find to three significant figures, the measure of A in radians. s = rθ 100 20 = θ π π θ = 20 100 = 0· 6283. . = 0· 628 radians

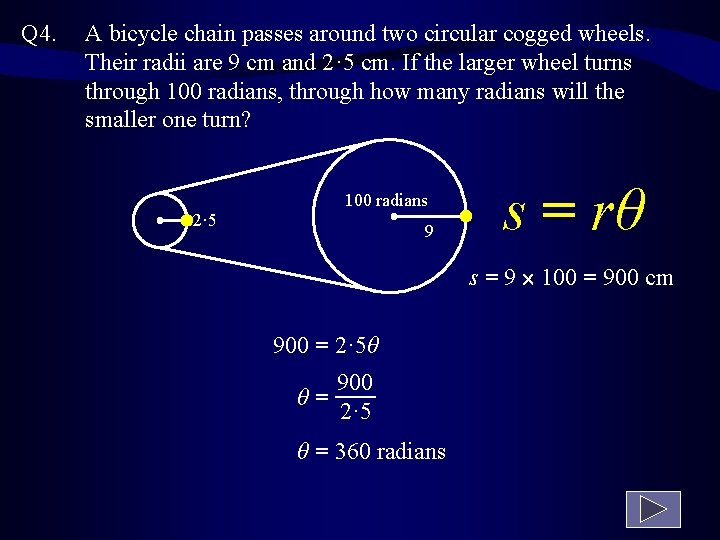
Q 4. A bicycle chain passes around two circular cogged wheels. Their radii are 9 cm and 2· 5 cm. If the larger wheel turns through 100 radians, through how many radians will the smaller one turn? 2· 5 100 radians 9 s = rθ s = 9 100 = 900 cm 900 = 2· 5θ 900 θ= 2· 5 θ = 360 radians

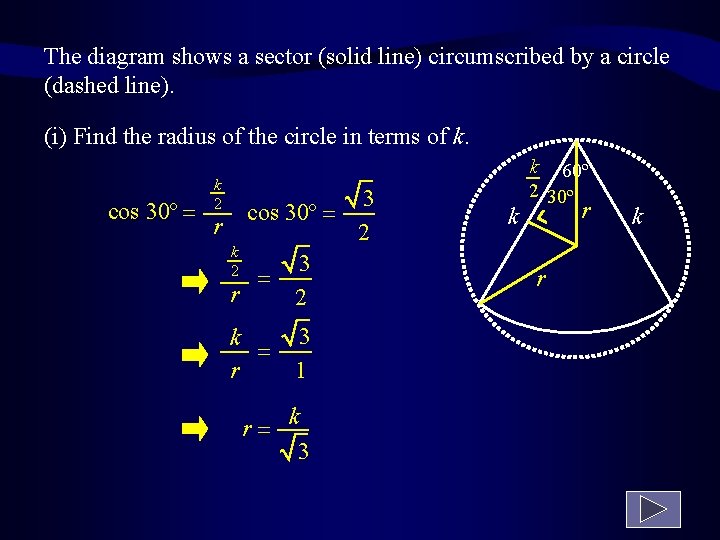
The diagram shows a sector (solid line) circumscribed by a circle (dashed line). (i) Find the radius of the circle in terms of k. cos 30º = k 2 3 cos 30º = r 2 k 3 2 = r 2 3 k = r 1 r= k 3 k k 60º 2 30º r r k

The diagram shows a sector (solid line) circumscribed by a circle (dashed line). (ii) Show that the circle encloses an area which is double that of the sector. r= Area of circle = π r 2 æ k ö 2 =πç ÷ è 3ø k 3 Twice area of sector Area of sector 3 k r r k