SECTION 7 4 ARC LENGTH ARC LENGTH v
















![THE ARC LENGTH FORMULA If f ’ is continuous on [a, b], then the THE ARC LENGTH FORMULA If f ’ is continuous on [a, b], then the](https://slidetodoc.com/presentation_image_h2/0d321aa941f2ed8b03a7f2900ba44f6f/image-19.jpg)



- Slides: 24

SECTION 7. 4 ARC LENGTH

ARC LENGTH v. What do we mean by the length of a curve? v. We might think of fitting a piece of string to the curve here and then measuring the string against a ruler. 7. 4 P 2

ARC LENGTH v. However, that might be difficult to do with much accuracy if we have a complicated curve. v. We need a precise definition for the length of an arc of a curve—in the same spirit as the definitions we developed for the concepts of area and volume. 7. 4 P 3

POLYGON v. If the curve is a polygon, we can easily find its length. n n We just add the lengths of the line segments that form the polygon. We can use the distance formula to find the distance between the endpoints of each segment. 7. 4 P 4

ARC LENGTH v. We are going to define the length of a general curve in the following way. n n First, we approximate it by a polygon. Then, we take a limit as the number of segments of the polygon is increased. 7. 4 P 5

ARC LENGTH v. This process is familiar for the case of a circle, where the circumference is the limit of lengths of inscribed polygons. 7. 4 P 6

ARC LENGTH v. Now, suppose that a curve C is defined by the equation y = f(x), where f is continuous and a ≤ x ≤ b. v. We obtain a polygonal approximation to C by dividing the interval [a, b] into n subintervals with endpoints x 0, x 1, …, xn and equal width Dx. 7. 4 P 7

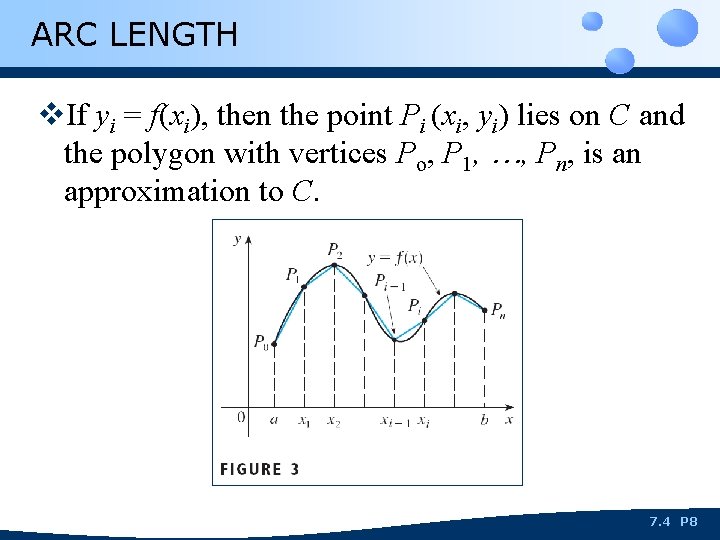
ARC LENGTH v. If yi = f(xi), then the point Pi (xi, yi) lies on C and the polygon with vertices Po, P 1, …, Pn, is an approximation to C. 7. 4 P 8

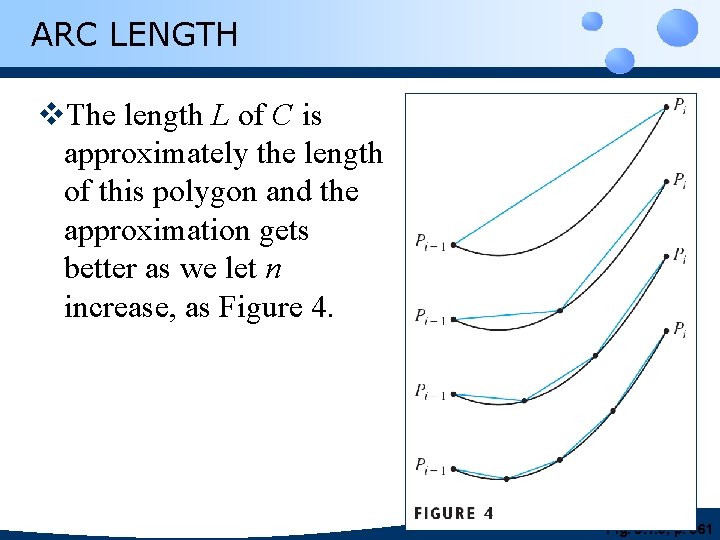
ARC LENGTH v. The length L of C is approximately the length of this polygon and the approximation gets better as we let n increase, as Figure 4. 7. 4 P 9 Fig. 9. 1. 3, p. 561

ARC LENGTH v. Here, the arc of the curve between Pi– 1 and Pi has been magnified and approximations with successively smaller values of Dx are shown. 7. 4 P 10

Definition 1 v. Thus, we define the length L of the curve C with equation y = f(x), a ≤ x ≤ b, as the limit of the lengths of these inscribed polygons (if the limit exists): 7. 4 P 11

ARC LENGTH v. Notice that the procedure for defining arc length is very similar to the procedure we used for defining area and volume. n n n First, we divided the curve into a large number of small parts. Then, we found the approximate lengths of the small parts and added them. Finally, we took the limit as n → ∞. 7. 4 P 12

ARC LENGTH v. The definition of arc length given by Equation 1 is not very convenient for computational purposes. n However, we can derive an integral formula for L in the case where f has a continuous derivative. v. Such a function f is called smooth because a small change in x produces a small change in f ’(x). 7. 4 P 13

SMOOTH FUNCTION v. If we let Dyi = yi – yi– 1, then 7. 4 P 14

SMOOTH FUNCTION v. By applying the Mean Value Theorem to f on the interval [xi– 1, xi], we find that there is a number xi* between xi– 1 and xi such that is, 7. 4 P 15

SMOOTH FUNCTION v. Thus, we have: 7. 4 P 16

SMOOTH FUNCTION v. Therefore, by Definition 1, 7. 4 P 17

SMOOTH FUNCTION v. We recognize this expression as being equal to vby the definition of a definite integral. n This integral exists because the function is continuous. v. Therefore, we have proved the following theorem. 7. 4 P 18
![THE ARC LENGTH FORMULA If f is continuous on a b then the THE ARC LENGTH FORMULA If f ’ is continuous on [a, b], then the](https://slidetodoc.com/presentation_image_h2/0d321aa941f2ed8b03a7f2900ba44f6f/image-19.jpg)
THE ARC LENGTH FORMULA If f ’ is continuous on [a, b], then the length of the curve y = f(x), a ≤ x ≤ b is: v. If we use Leibniz notation for derivatives, we can write the arc length formula as: 7. 4 P 19

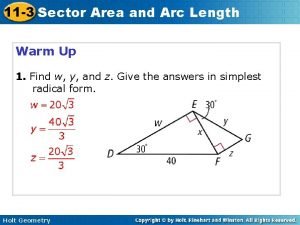
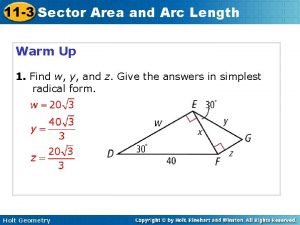
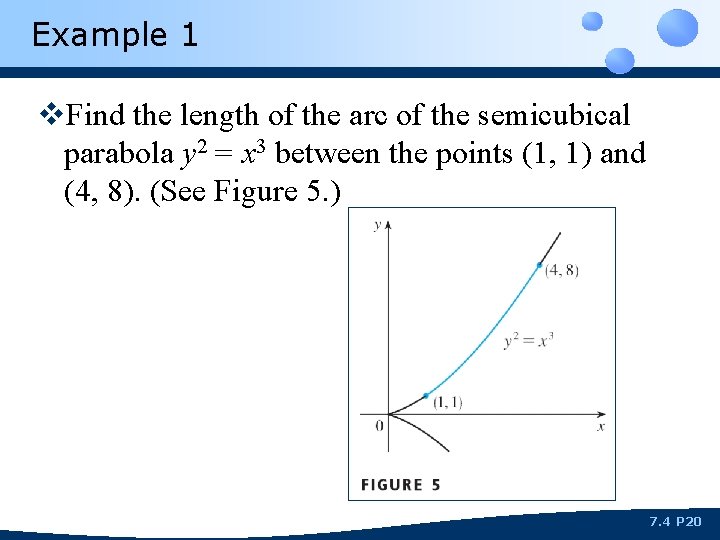
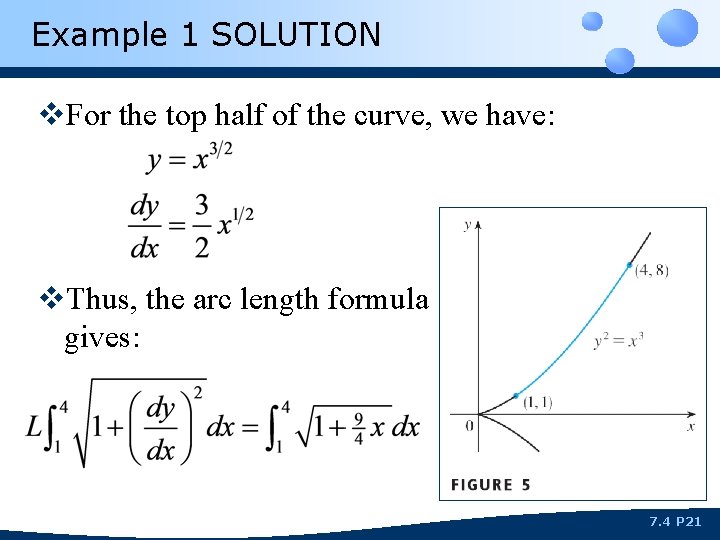
Example 1 v. Find the length of the arc of the semicubical parabola y 2 = x 3 between the points (1, 1) and (4, 8). (See Figure 5. ) 7. 4 P 20

Example 1 SOLUTION v. For the top half of the curve, we have: v. Thus, the arc length formula gives: 7. 4 P 21

Example 1 SOLUTION v. If we substitute u = 1 + (9/4)x, then du = (9/4) dx. v. When x = 1, u = 13/4. v. When x = 4, u = 10. v. Therefore, 7. 4 P 22

ARC LENGTH v. If a curve has the equation x = g(y), c ≤ y ≤ d, and g’(y) is continuous, then by interchanging the roles of x and y in Formula 2 or Equation 3, we obtain its length as: 7. 4 P 23

Example 2 v. Find the length of the arc of the parabola y 2 = x from (0, 0) to (1, 1). v. SOLUTION n n Since x = y 2, we have dx/dy = 2 y. Then, Formula 4 gives: 7. 4 P 24
 Arc promoteur vs arc investigateur
Arc promoteur vs arc investigateur Parts of a circle
Parts of a circle Major arc
Major arc Arc emu88 com arc info 05 100005 html
Arc emu88 com arc info 05 100005 html Area of sector radians
Area of sector radians How to find an angle measure in a circle
How to find an angle measure in a circle Dcen welding definition
Dcen welding definition Khan academyn
Khan academyn Circumference of a half dollar
Circumference of a half dollar Circumference
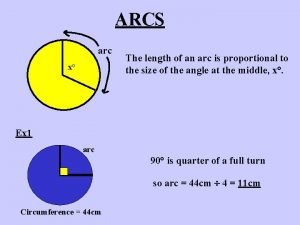
Circumference Arc length formula
Arc length formula Module 16 arc length and sector area answer key
Module 16 arc length and sector area answer key Area of a sector formula radians
Area of a sector formula radians Arc length worksheet
Arc length worksheet Arc length worksheet
Arc length worksheet Arc length formula calculus
Arc length formula calculus Arc length corollary
Arc length corollary Arc length and curvature
Arc length and curvature Area of sector
Area of sector 12-3 sector area and arc length
12-3 sector area and arc length Arc length versus sector area
Arc length versus sector area Circumference and arc length assignment
Circumference and arc length assignment 11-3 practice b sector area and arc length
11-3 practice b sector area and arc length 12-3 sector area and arc length
12-3 sector area and arc length Polar derivative formula
Polar derivative formula