Trees Part 1 Theoretical CSE 2320 Algorithms and

Trees (Part 1, Theoretical) CSE 2320 – Algorithms and Data Structures University of Texas at Arlington 10/30/2021 1

Trees • Trees are a natural data structure for representing specific data. – Family trees. – Organizational chart of a corporation, showing who supervises who. – Folder (directory) structure on a hard drive. 2

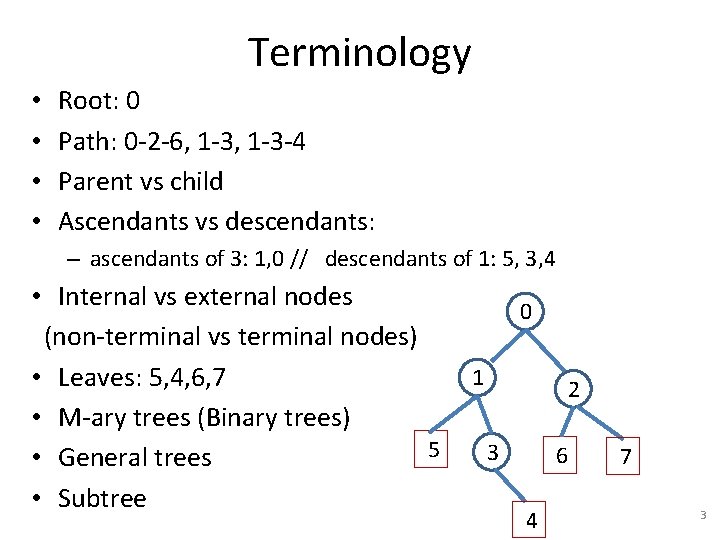
Terminology • • Root: 0 Path: 0 -2 -6, 1 -3 -4 Parent vs child Ascendants vs descendants: – ascendants of 3: 1, 0 // descendants of 1: 5, 3, 4 • Internal vs external nodes (non-terminal vs terminal nodes) • Leaves: 5, 4, 6, 7 • M-ary trees (Binary trees) 5 • General trees • Subtree 0 1 2 3 6 4 7 3

Terminology • If Y is the parent of X, then X is called a child of Y. – The root has no parents. – Every other node, except for the root, has exactly one parent. • A node can have 0, 1, or more children. • Nodes that have children are called internal nodes • Nodes that have no children are called external nodes, or leaves. 4

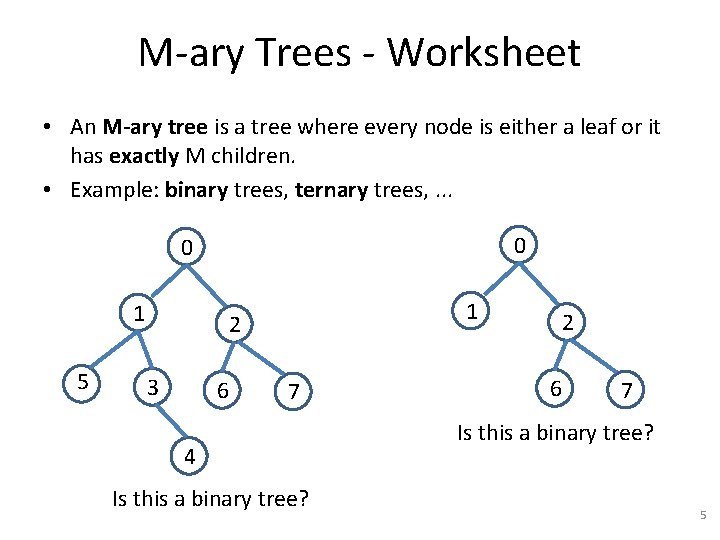
M-ary Trees - Worksheet • An M-ary tree is a tree where every node is either a leaf or it has exactly M children. • Example: binary trees, ternary trees, . . . 0 0 1 5 1 2 3 6 7 4 Is this a binary tree? 2 6 7 Is this a binary tree? 5

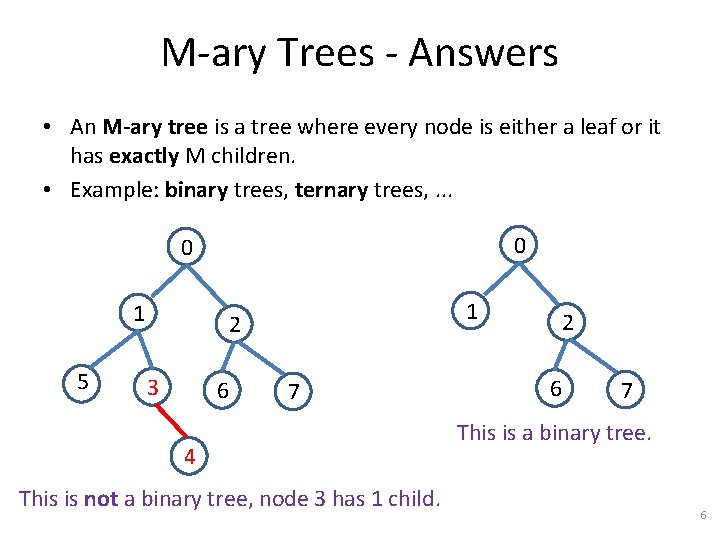
M-ary Trees - Answers • An M-ary tree is a tree where every node is either a leaf or it has exactly M children. • Example: binary trees, ternary trees, . . . 0 0 1 5 1 2 3 6 7 4 This is not a binary tree, node 3 has 1 child. 2 6 7 This is a binary tree. 6

Types of binary trees Perfect tree • Perfect – each internal node has exactly 2 children and all the leaves are on the same level. – E. g. ancestry tree (anyone will have exactly 2 parents). • Full – every node has exactly 0 or 2 children. – E. g. tree generated by the Fibonacci recursive calls. – Binary tree. • Complete tree – every level, except for possibly the last one is completely filled and on the last level, all the nodes are as far on the left as possible. – E. g. the heap tree. – Height: and it can be stored as an array. Reference: wikipedia (https: //en. wikipedia. org/wiki/Binary_tree) Complete tree 7

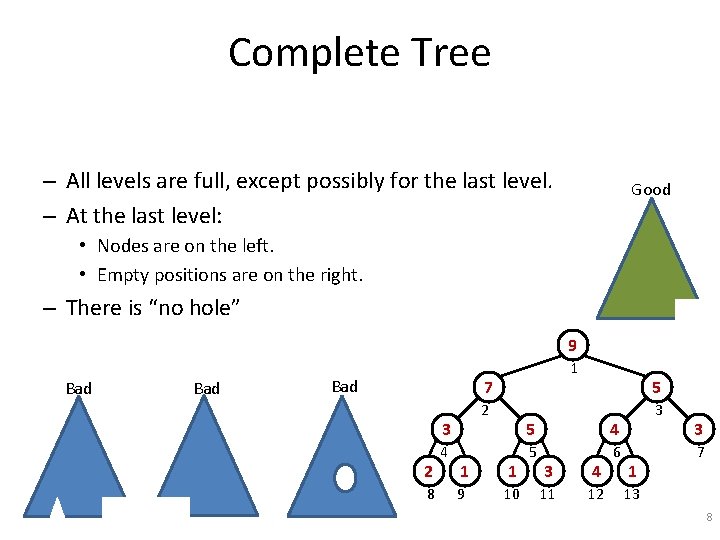
Complete Tree – All levels are full, except possibly for the last level. – At the last level: Good • Nodes are on the left. • Empty positions are on the right. – There is “no hole” 9 Bad Bad 1 7 2 3 2 8 4 1 1 9 10 5 5 4 5 6 3 4 11 12 3 1 3 7 13 8

Worksheet • Self study: Give examples of trees that are: – – Perfect Full but not complete Complete but not full Neither full not complete 9

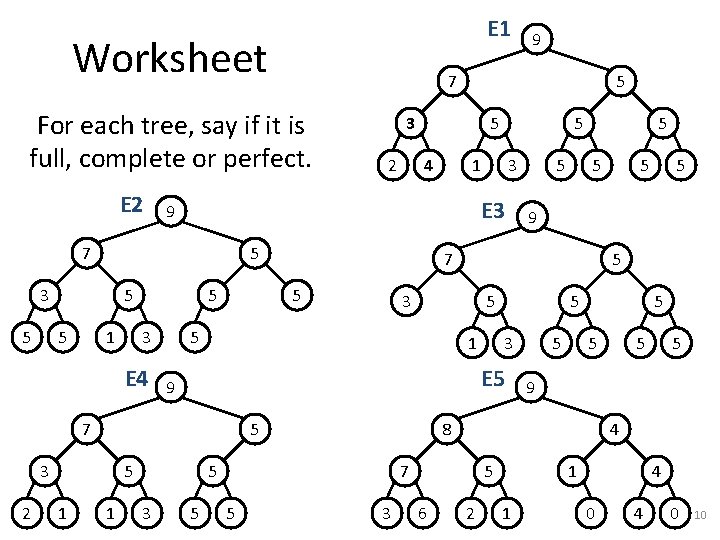
E 1 Worksheet 7 For each tree, say if it is full, complete or perfect. E 2 5 1 5 3 E 4 3 3 5 5 5 9 4 5 6 5 9 8 7 5 5 5 E 5 9 5 5 1 5 3 3 5 5 5 1 1 3 5 3 1 4 5 7 2 2 5 E 3 5 5 3 5 9 7 9 2 1 1 4 0 10

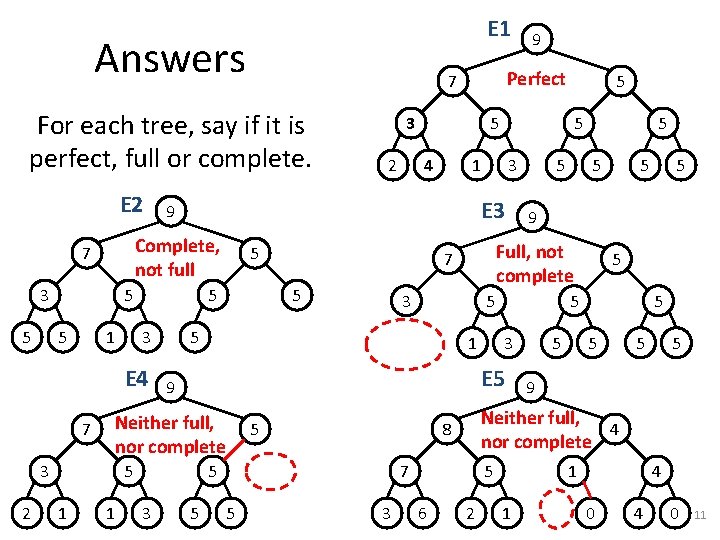
E 1 Answers E 2 3 5 1 7 3 2 1 5 3 5 9 3 5 6 5 5 5 5 9 Neither full, 4 nor complete 8 7 5 5 5 E 5 9 5 5 5 1 5 3 3 5 Full, not complete 3 5 5 1 7 5 Neither full, nor complete 3 4 5 5 E 4 2 5 5 E 3 5 5 3 9 Complete, not full 7 Perfect 7 For each tree, say if it is perfect, full or complete. 9 2 1 1 4 0 11

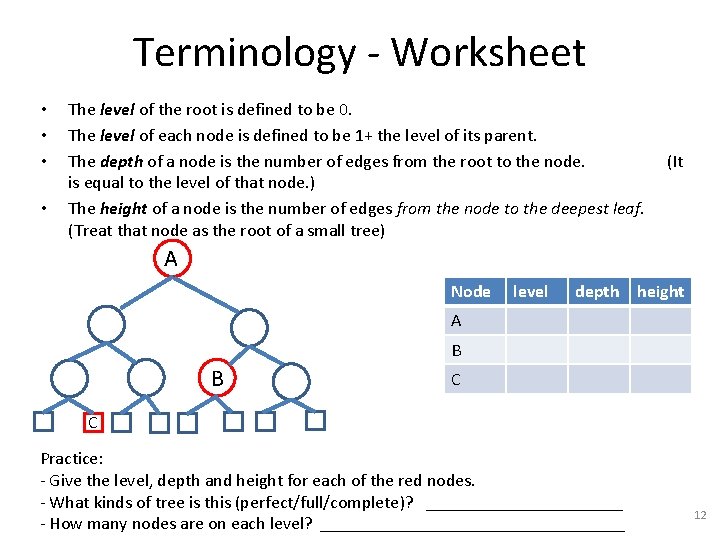
Terminology - Worksheet • • The level of the root is defined to be 0. The level of each node is defined to be 1+ the level of its parent. The depth of a node is the number of edges from the root to the node. is equal to the level of that node. ) The height of a node is the number of edges from the node to the deepest leaf. (Treat that node as the root of a small tree) (It A Node level depth height A B B C C Practice: - Give the level, depth and height for each of the red nodes. - What kinds of tree is this (perfect/full/complete)? ___________ - How many nodes are on each level? _________________ 12

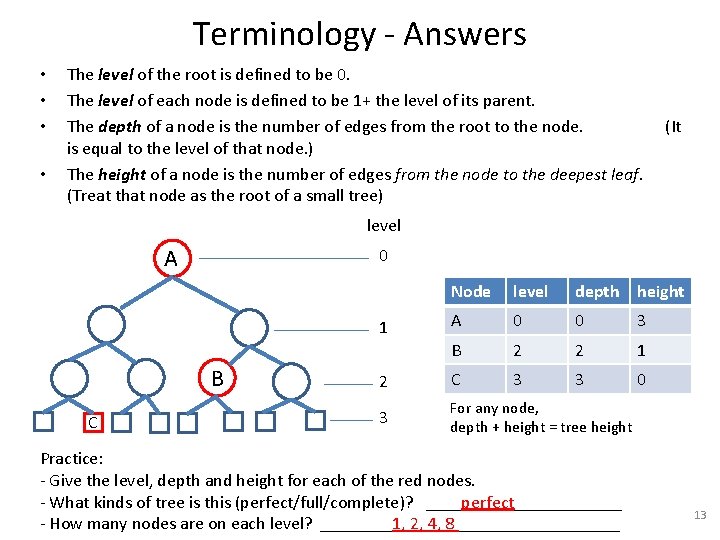
Terminology - Answers • • The level of the root is defined to be 0. The level of each node is defined to be 1+ the level of its parent. The depth of a node is the number of edges from the root to the node. is equal to the level of that node. ) The height of a node is the number of edges from the node to the deepest leaf. (Treat that node as the root of a small tree) (It level A 0 Node level depth height A 0 0 3 B 2 2 1 2 C 3 3 0 3 For any node, depth + height = tree height 1 B C Practice: - Give the level, depth and height for each of the red nodes. - What kinds of tree is this (perfect/full/complete)? ____perfect______ - How many nodes are on each level? ____1, 2, 4, 8 _________ 13

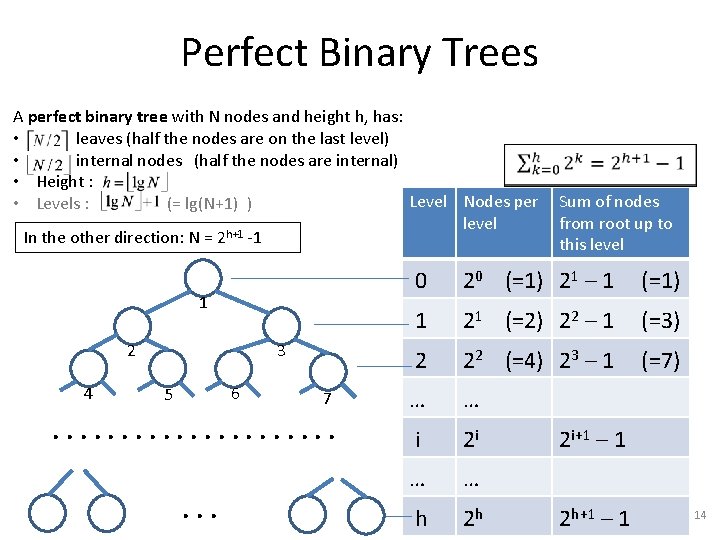
Perfect Binary Trees A perfect binary tree with N nodes and height h, has: • leaves (half the nodes are on the last level) • internal nodes (half the nodes are internal) • Height : Level Nodes per • Levels : (= lg(N+1) ) level In the other direction: N = 2 h+1 -1 1 2 4 3 6 5 7 . . . Sum of nodes from root up to this level 0 20 (=1) 21 – 1 (=1) 1 21 (=2) 22 – 1 (=3) 2 22 (=4) 23 – 1 (=7) … … i 2 i … … h 2 h 2 i+1 – 1 2 h+1 – 1 14

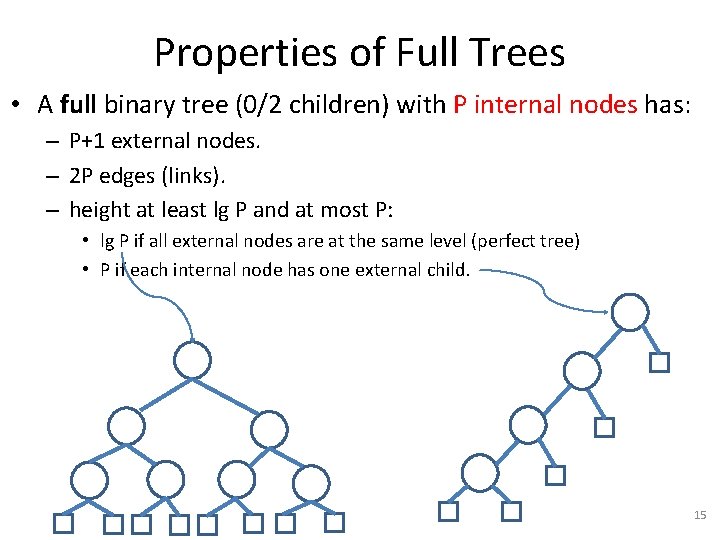
Properties of Full Trees • A full binary tree (0/2 children) with P internal nodes has: – P+1 external nodes. – 2 P edges (links). – height at least lg P and at most P: • lg P if all external nodes are at the same level (perfect tree) • P if each internal node has one external child. 15

Proof Prove that a full tree with P internal nodes has P+1 external leaves. • Full tree property: • What proof style will you use? Can you prove such a relation for 3 -trees? 4 -trees? 16