This slide intentionally left blank The Rayleigh Plateau

This slide intentionally left blank

The Rayleigh Plateau Instability By Mike Cromer and Patrick C. Rowe

The Rayleigh-Plateau Instability Introduction The Rayleigh-Plateau Instability is a phenomenon which occurs in columns of fluid. A column of fluid will experience small perturbations from perfection. This may be from existing internal motions or from influences in the outside environment, like wind or breath. Certain wavelengths of these perturbations are magnified over time and cause the column to break up into droplets. Most people are familiar with this phenomenon. It is what causes the water flowing from a hose to break into drops, or a thin stream from a faucet to develop waves or break up before hitting the bottom of the sink.

The Rayleigh-Plateau Instability Introduction In this presentation, we will derive the necessary condition for a perturbation to cause instability and eventual break up of the column. Then we will make a calculation to determine the fastest growing perturbation. This will allow us to predict the spacing of drops resulting from the break up of the column. Next, we will discuss the shape of the final drops in the experiments we have run in exploration of this phenomenon and difficulties in deriving these shapes from the equations governing this phenomenon. Finally, we will make a comparison between the wavelength predicted by the equations and the wavelength observed in the laboratory.

The Rayleigh-Plateau Instability Derivation of Necessary Condition for Instability We follow a derivation due to Jen Eggers in the 'Reviews of Modern Physics. ' We assume that the cylinder is initially perfect and undergoes a sinusoidal perturbation of wavelength on the cylinder. There may be many of these perturbations, but we assume that they combine in a linear fashion and therefore, we can consider each one separately.

The Rayleigh-Plateau Instability Derivation of Necessary Condition for Instability It is clear that the volume does not vary as the cylinder evolves. To the side, we integrate our equation, examine the resulting volume and then add a perturbation expansion beginning with terms of a smaller order than the perturbation to keep the volume constant.

The Rayleigh-Plateau Instability Derivation of Necessary Condition for Instability Ultimately, we understand from fluid dynamics that the fluid will seek to minimize surface area. So we find the surface area of the perturbed cylinder. Note that 'n' can take on only integer values, so we see right away that if n is larger than 0, the perturbation will increase the surface area. This is a stable perturbation, as the surface tension forces will counteract it and return the surface to its previous state. However, if n=0, there is the possibility of a decreasing surface area. This happens when k<1. Looking back at the definition of k, we see that this means that in order for a perturbation to grow and cause the surface to depart from cylindrical, the wavelength must be greater than 2 Pi times the radius of the initial cylinder.

The Rayleigh-Plateau Instability Derivation of Fastest Growing Wavelength In this section of the presentation, we assume that the fluid is inviscid and irrotational. Therefore, there is a velocity potential, , and we can use the equations for an ideal fluid. Non-dimensionalize Surface moves according to which gives Where the capital D's denote the material derivative.

The Rayleigh-Plateau Instability Derivation of Fastest Growing Wavelength The evolution of on the boundary is given by Bernoulli's equation, with the pressure given by the Young-Laplace formula. To consider the Lagrangian evolution of the surface, we change the time derivative to the material derivative, and to satisfy Bernoulli's equation, we need: Which finally gives us

The Rayleigh-Plateau Instability Derivation of Fastest Growing Wavelength Now, using the condition that the initial velocity is zero, which implies that is initially zero, and to the first order, we find that C=1. The result is 3 non-dimensional equations which describe the motion of the boundary and two initial conditions. (Note that the second and third equations only hold on the boundary. )

The Rayleigh-Plateau Instability Derivation of Fastest Growing Wavelength The perturbation is small, so we assume that the velocity is small and attempt a solution in the form: For convenience, we write r for r* from now on. Inserting our guess, we get to the first order in epsilon an equation and two boundary conditions:

The Rayleigh-Plateau Instability Derivation of Fastest Growing Wavelength We look for solutions of our first order equations in the form: From the first equation we get: The only solution which is regular for r=0 is: Substituting into the b. c. 's gives: Applying the initial conditions derived from our earlier conditions:

The Rayleigh-Plateau Instability Derivation of Fastest Growing Wavelength We get solutions: Where is the frequency nondimensionalized by 1/t 0: This is the equation to be maximized.

The Rayleigh-Plateau Instability Derivation of Fastest Growing Wavelength We rely on Eggers solution because values of the modified Bessel functions must be looked up anyways. The value of k which maximizes is. 0697. This corresponds to the Rayleigh mode which is given by

The Rayleigh-Plateau Instability Comparison of Experiment and Numerical Result Motor Oil Initial cylinder radius: a =. 028 cm Predicted minimum: Smallest wavelength measured: . 224 cm Predicted dominant: Longest wavelength measured: . 406 cm

The Rayleigh-Plateau Instability Comparison of Experiment and Numerical Result Possible Reasons for Discrepancies Perhaps there was not enough time for the fastest growing mode to become the most influential. Also, the Rayleigh-Plateau instability models fluid columns inside of other fluids. It may not be the correct model for an annulus of fluid around a solid cylinder, but simply a good springboard to explain this situation.

The Rayleigh-Plateau Instability Bead Shape We will now assume that the beads are radially and axially symmetric (the latter was shown in the previous analysis). With these assumptions, we have that the energy on the surface is given by: We also know that the volume must remain constant, thus giving us the volume constraint:

The Rayleigh-Plateau Instability Bead Shape

The Rayleigh-Plateau Instability Bead Shape

The Rayleigh-Plateau Instability Bead Shape We now use the motor oil experiment to obtain the values of our constants. Using information provided on the web and the measuring technique detailed in the procedure section, we have: Finally, using the explicit Euler method to solve the 1 st order nonlinear ode numerically, we obtain the following shape of the top-right part of a bead:
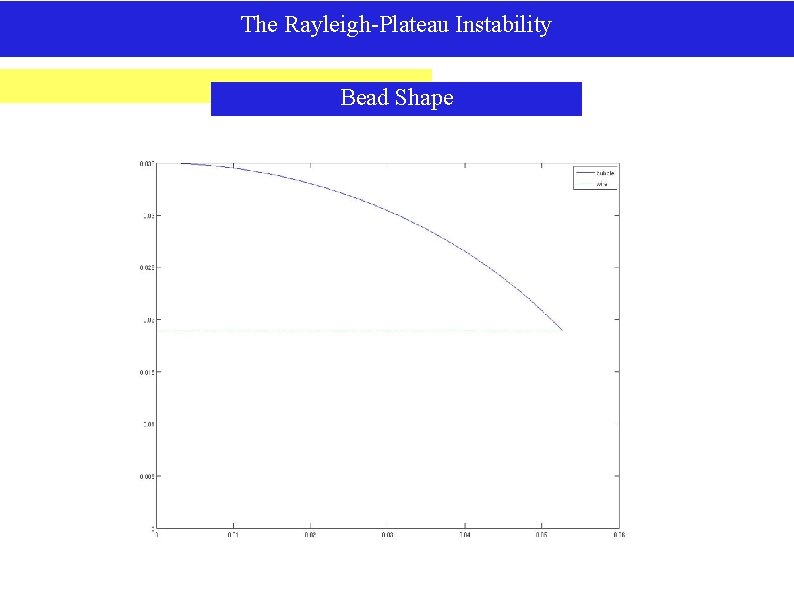
The Rayleigh-Plateau Instability Bead Shape
- Slides: 21