The Search for Simple Symmetric Venn Diagrams Torsten

The Search for Simple Symmetric Venn Diagrams Torsten Mütze, ETH Zürich Talk mainly based on [Griggs, Killian, Savage 2004]

Venn Diagrams • Introduced by John Venn (1834– 1923) for • representing “propositions and reasonings” Def: n-Venn diagram - n Jordan curves in the plane - finitely many intersections - For each the region is nonempty and connected (=>2 n regions in total) B A C n=3 simple non-simple

Existence for all n? • It won’t work with n circles: • • Theorem (Venn 1880): There is a simple n-Venn diagram for every n. Proof: Induction over n with invariant: last curve added touches every region exactly once Cn+1 n=3 Cn

Existence for all n n=4 n=5 n=6 What about diagrams that look “more nicely”?

Symmetric diagrams for all n? • Def: (n-fold) symmetric Venn diagram Rotation of one curve around a fixed point yields all others n=3 n=5 100 n=7 101 110 001 111 010 000 • • Def: characteristic vector of a region inside Def: rank of a region = number of curves for which region is inside = number of 1’s in char. vect 0 r => regions of rank r

Symmetric diagrams for all n? n=4 regions of rank 2 6 is not divisible by 4 => no symmetric 4 -Venn diagram • Theorem (Henderson 1963): Necessary for the existence of a symmetric n-Venn diagram is that n is prime. • Proof: is divisible by n for all iff n is prime (Leibniz)

Symmetric diagrams for all prime n • Theorem (Griggs, Killian, Savage 2004): If n is prime, then there is a symmetric n-Venn diagram. non-simple n=5 n=11

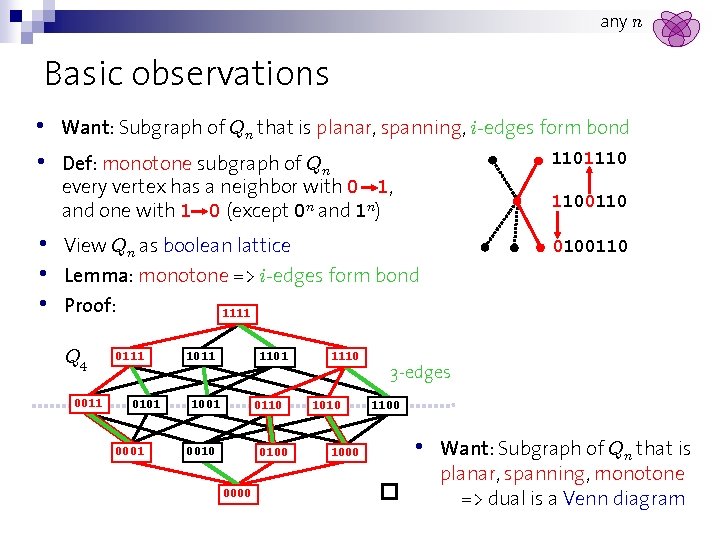
any n Basic observations • • • Forget about symmetry for the moment (following holds for any n) View Venn diagram as (multi)graph G Observation: Geometric dual G‘ is a subgraph of Qn 3 -edges n=3 100 n=4 100 101 G 101 110 111 001 011 G‘=Q 3 • • prime n 111 010 G 110 001 G‘ 000 G‘=Q 4 minus 4 edges Idea: Reverse the construction Want: Subgraph G‘ of Qn that is • planar • spanning • dual edges of the i-edges in G‘ form a cycle in G <=> i-edges form bond (G‘ minus i-edges has exactly two components)

any n Basic observations • • • Want: Subgraph of Qn that is planar, spanning, i-edges form bond Def: monotone subgraph of Qn every vertex has a neighbor with 0 1, and one with 1 0 (except 0 n and 1 n) 1101110 View Qn as boolean lattice Lemma: monotone => i-edges form bond 0100110 Proof: Q 4 0011 1100110 1111 0101 0001 1011 1101 1001 0110 0010 0100 0000 1110 1000 3 -edges 1100 • Want: Subgraph of Qn that is planar, spanning, monotone => dual is a Venn diagram

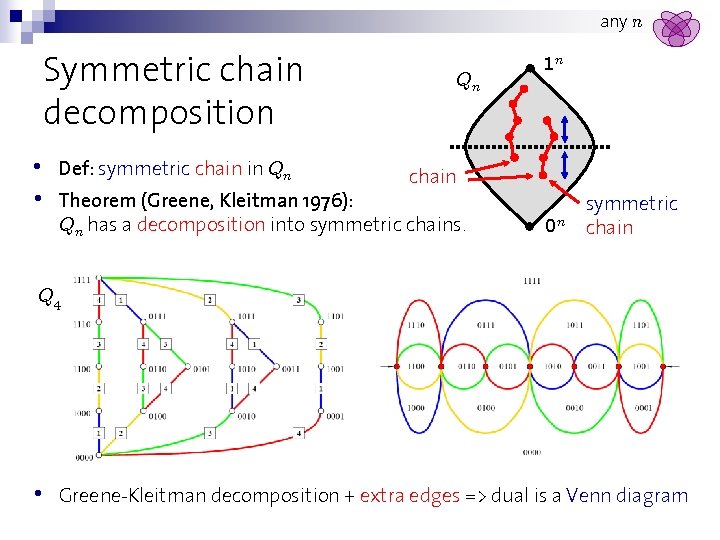
any n Symmetric chain decomposition • • Def: symmetric chain in Qn Qn 1 n chain Theorem (Greene, Kleitman 1976): Qn has a decomposition into symmetric chains. 0 n symmetric chain Q 4 • Greene-Kleitman decomposition + extra edges => dual is a Venn diagram

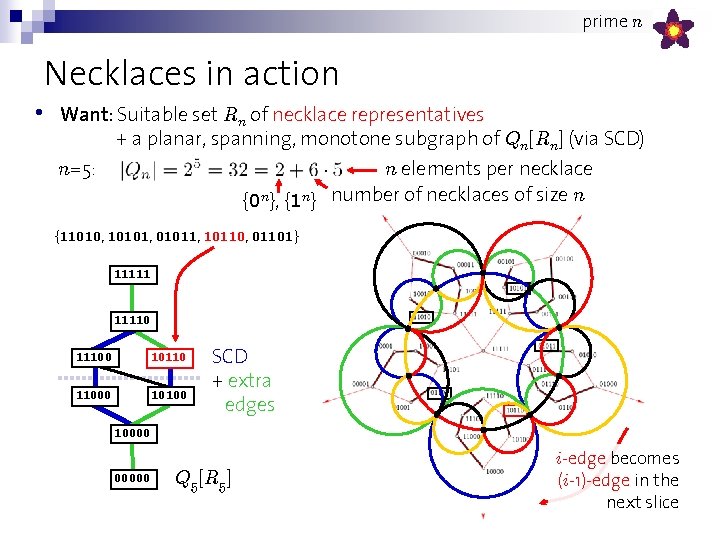
prime n How to achieve symmetry • • Now suppose n is prime • • Prime n => natural partition of Qn into n symmetric classes n=5 Idea: Work within “ 1/n-th” of Qn to obtain “ 1/n-th” of Venn diagram, then rotate Def: necklace = set of all n-bit strings that differ by rotation n=5: {11010, 10101, 01011, 10110, 01101} {11000, 10001, 00011, 00110, 01100} 2 necklaces • Observation: Prime n => each necklace has exactly n elements (except {0 n} and {1 n}) • Want: Suitable set Rn of necklace representatives + a planar, spanning, monotone subgraph of Qn[Rn] (via SCD) => symmetric Venn diagram

prime n Necklaces in action • Want: Suitable set Rn of necklace representatives + a planar, spanning, monotone subgraph of Qn[Rn] (via SCD) n=5: n elements per necklace {0 n}, {1 n} number of necklaces of size n {11010, 10101, 01011, 10110, 01101} 111110 11100 10110 11000 10100 SCD + extra edges 100000 Q 5[R 5] i-edge becomes (i-1)-edge in the next slice

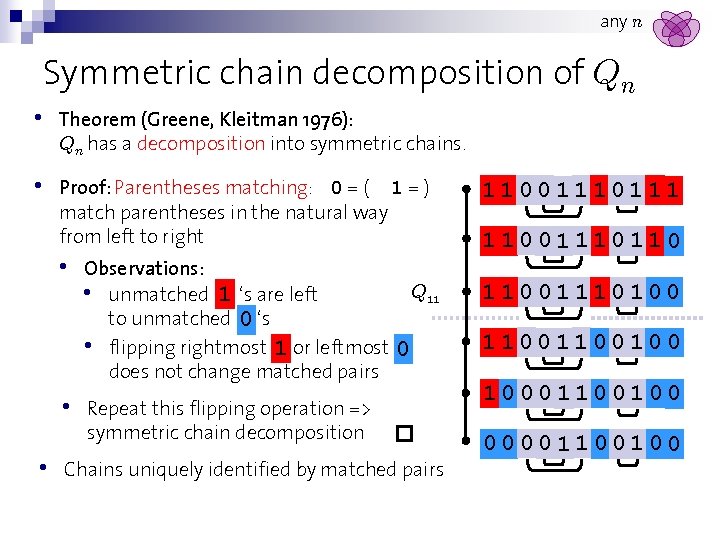
any n Symmetric chain decomposition of Qn • Theorem (Greene, Kleitman 1976): Qn has a decomposition into symmetric chains. • Proof: Parentheses matching: 0 = ( 1 = ) match parentheses in the natural way from left to right • • • Observations: • unmatched 1 ‘s are left to unmatched 0 ‘s • flipping rightmost 1 or leftmost does not change matched pairs Q 11 0 Repeat this flipping operation => symmetric chain decomposition Chains uniquely identified by matched pairs 11001110110 11001110100 1100100 10001100100 00001100100

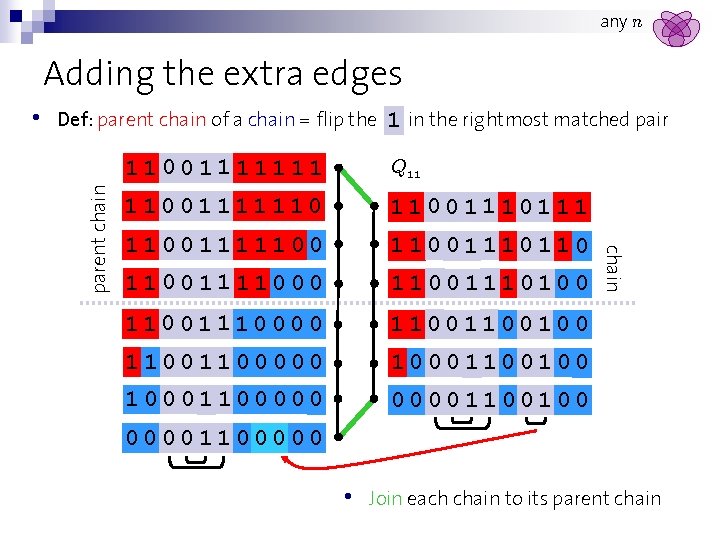
any n Adding the extra edges Def: parent chain of a chain = flip the 1 in the rightmost matched pair 11001111111 Q 11 11001111110 110011111001110110 11001111000 11001110100 11001110000 1100100 1100000 10001100100 100011000001100100 chain parent chain • 00001100000 • Join each chain to its parent chain

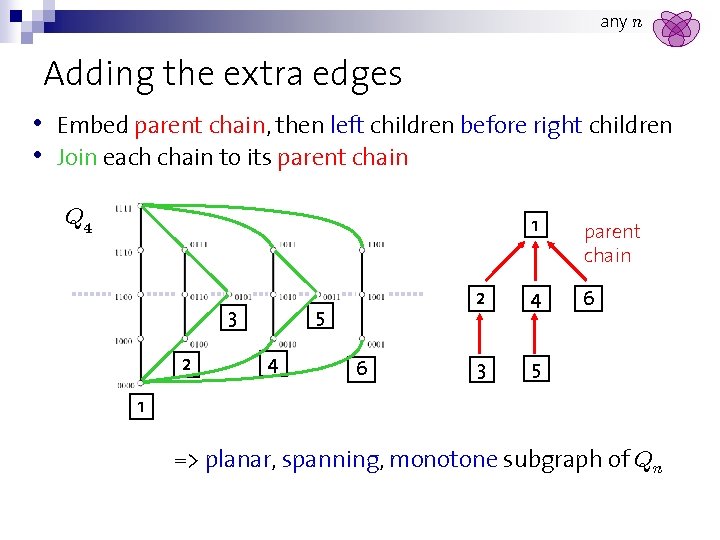
any n Adding the extra edges • Embed parent chain, then left children before right children • Join each chain to its parent chain Q 4 5 3 2 4 6 1 parent chain 2 4 6 3 5 1 => planar, spanning, monotone subgraph of Qn

prime n Symmetric chain decomposition of Qn[Rn] • Main contribution of [Griggs, Killian, Savage 2004] Def: block code of a 0 -1 -string n=11: 0 xxxxxxxxxx 1 1100100 (4 , • • 4 , 3) (∞) necklace • 11001001 001100100110 11001001100 10010011 01001100 00110010 block code (4, 4, 3) (∞) (∞) (4, 3, 4) (∞) (∞) (3, 4, 4) (∞) Observations: In each necklace (except {0 n} and {1 n}) • at least one finite block code • all finite block codes differ by rotation • n prime: no two elements with same finite block code From each necklace select element with lexicographically smallest block code as representative => Rn

prime n Symmetric chain decomposition of Qn[Rn] • Observation: Block codes within Greene-Kleitman chain do not change (except (∞) at both ends) => chain with one element from Rn contains only elements from Rn => symmetric chain decomposition of Qn[Rn] • Add extra edges between chains to obtain planar, spanning, monotone subgraph of Qn[Rn] Q 11[R 11] block code 11011001111 (∞) 11011001110 (3, 4, 4) 1101100 (3, 4, 4) 11010001100 (3, 4, 4) 10010001100 (3, 4, 4) 0001100 (∞)

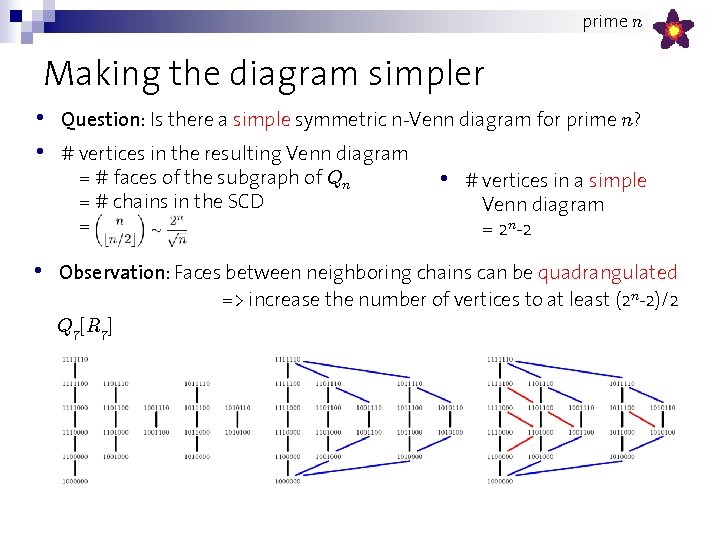
prime n Making the diagram simpler • • • Question: Is there a simple symmetric n-Venn diagram for prime n? # vertices in the resulting Venn diagram = # faces of the subgraph of Qn = # chains in the SCD = • # vertices in a simple Venn diagram = 2 n-2 Observation: Faces between neighboring chains can be quadrangulated => increase the number of vertices to at least (2 n-2)/2 Q 7[R 7]

Thank you! Questions?

References • Jerrold Griggs, Charles E. Killian, and Carla D. Savage. Venn diagrams and symmetric chain decompositions in the Boolean lattice. Electron. J. Combin. , 11: Research Paper 2, 30 pp. (electronic), 2004. [Griggs, Killian, Savage 2004] • Charles E. Killian, Frank Ruskey, Carla D. Savage, and Mark Weston. Half-simple symmetric Venn diagrams. Electron. J. Combin. , 11: Research Paper 86, 22 pp. (electronic), 2004. • Frank Ruskey. A survey of Venn diagrams. Electron. J. Combin. , 4(1): Dynamic Survey 5 (electronic), 2001.