Lesson 2 2 Venn Diagrams and Logic Venn

  • Slides: 31
Download presentation
Lesson 2 -2 Venn Diagrams and Logic

Lesson 2 -2 Venn Diagrams and Logic

Venn diagrams: • show relationships between different sets of data. • can represent conditional

Venn diagrams: • show relationships between different sets of data. • can represent conditional statements.

A Venn diagram is usually drawn as a circle. • Every point IN the

A Venn diagram is usually drawn as a circle. • Every point IN the circle belongs to that set. • Every point OUT of the circle does not. . B DOGS . A A=poodle. . . a dog B= horse. . . NOT a dog . . . B dog

Many Venn diagrams are drawn as two overlapping circles. A is in Group 1

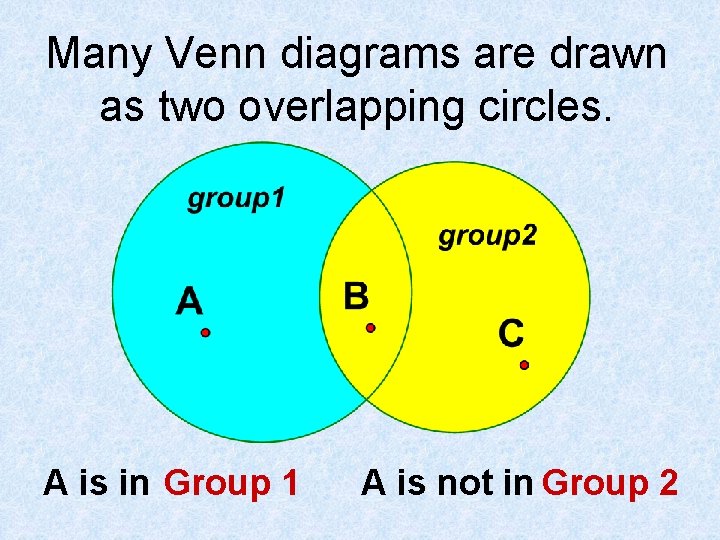
Many Venn diagrams are drawn as two overlapping circles. A is in Group 1 A is not in Group 2

Many Venn diagrams are drawn as two overlapping circles B is in Group 1

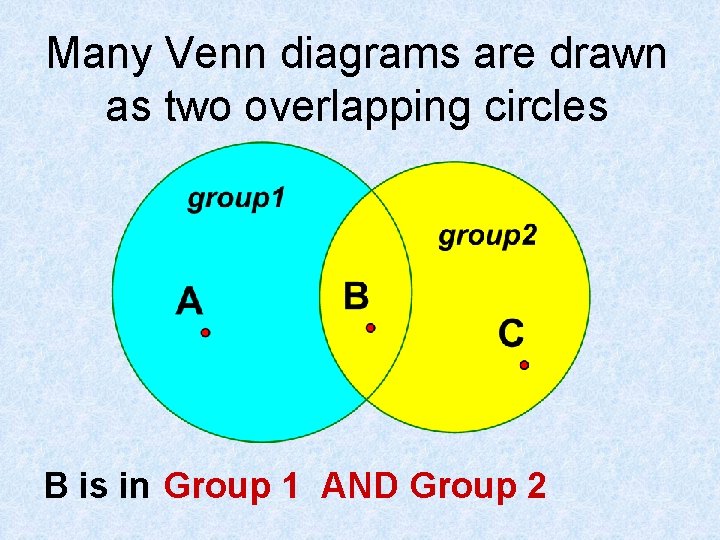
Many Venn diagrams are drawn as two overlapping circles B is in Group 1 AND Group 2

Many Venn diagrams are drawn as two overlapping circles C is in Group 2

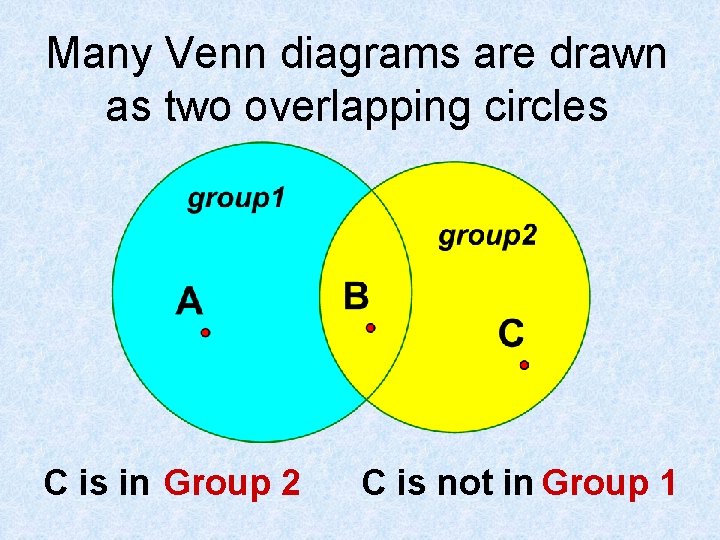
Many Venn diagrams are drawn as two overlapping circles C is in Group 2 C is not in Group 1

Many Venn diagrams are drawn as two overlapping circles Some of the elements in

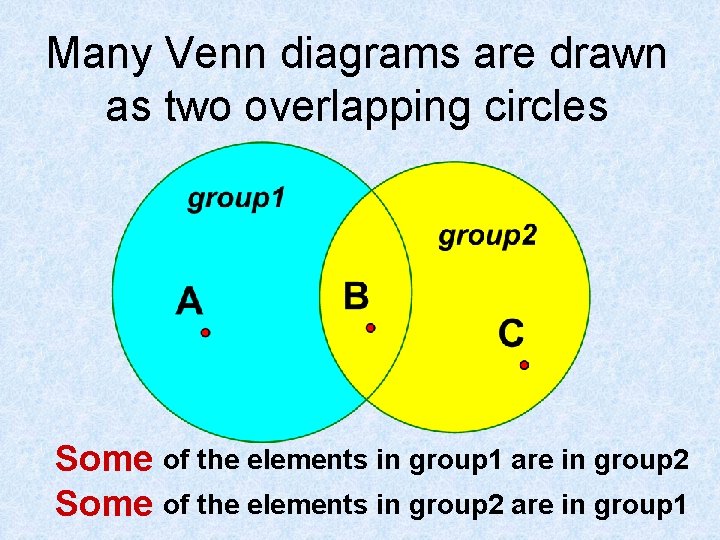
Many Venn diagrams are drawn as two overlapping circles Some of the elements in group 1 are in group 2 Some of the elements in group 2 are in group 1

Sometimes the circles do not overlap in a Venn diagram. D is in Group

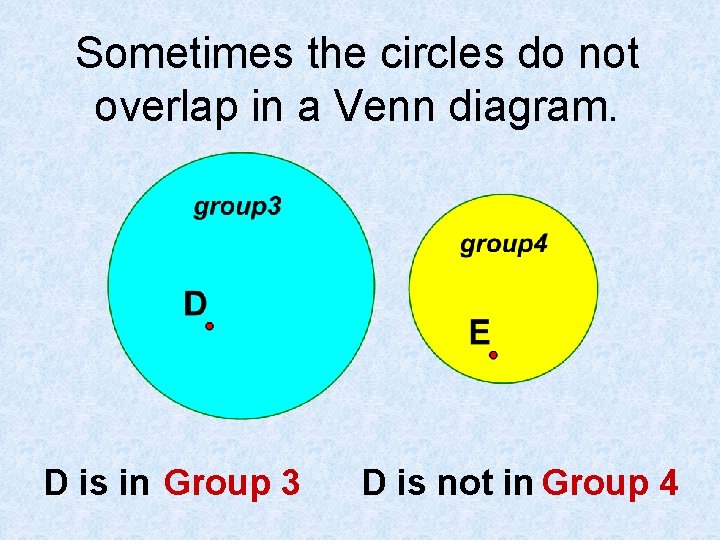
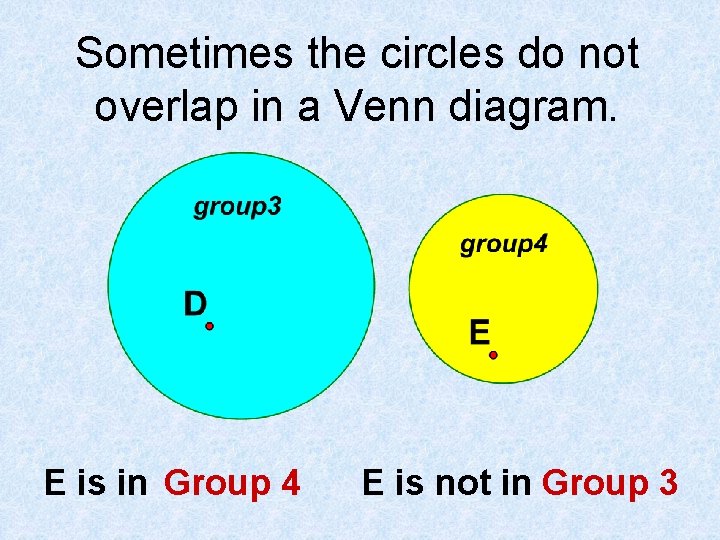
Sometimes the circles do not overlap in a Venn diagram. D is in Group 3 D is not in Group 4

Sometimes the circles do not overlap in a Venn diagram. E is in Group

Sometimes the circles do not overlap in a Venn diagram. E is in Group 4 E is not in Group 3

Sometimes the circles do not overlap in a Venn diagram. None of the elements

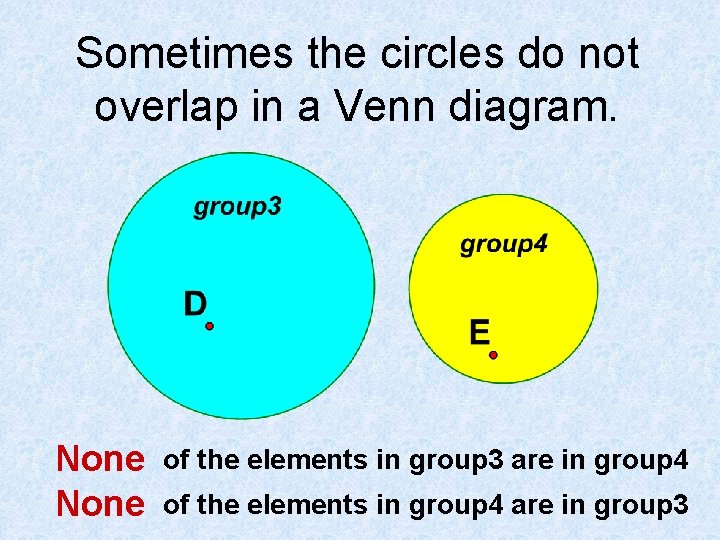
Sometimes the circles do not overlap in a Venn diagram. None of the elements in group 3 are in group 4 of the elements in group 4 are in group 3

In Venn diagrams it is possible to have one circle inside another. F is

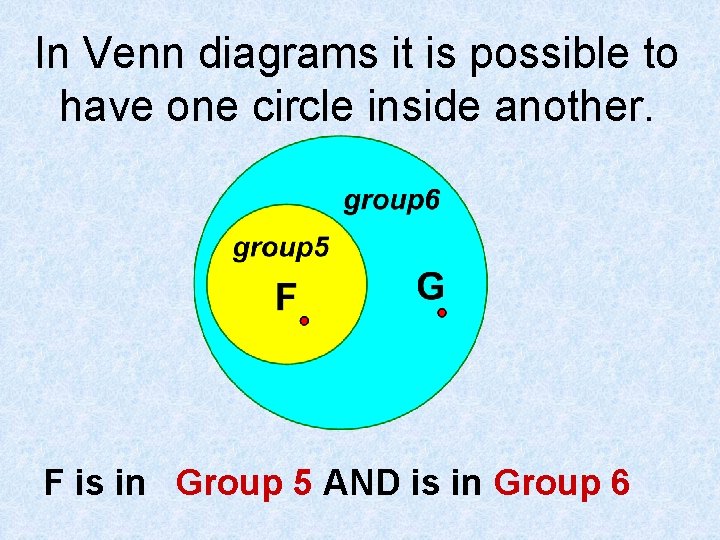
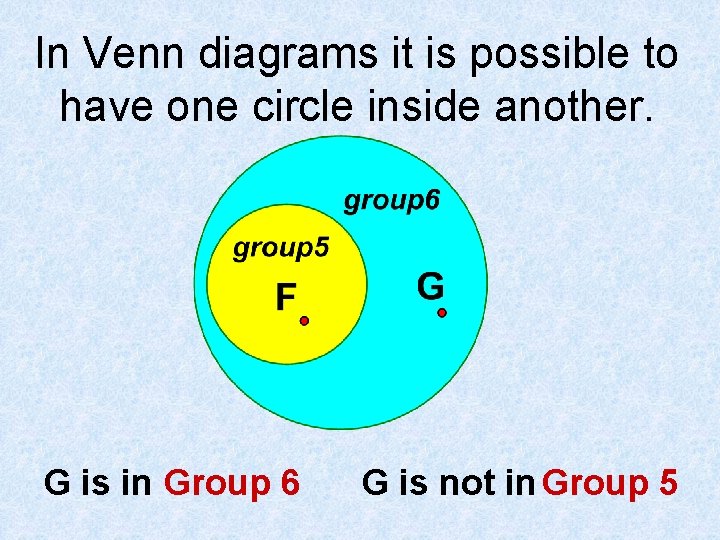
In Venn diagrams it is possible to have one circle inside another. F is in Group 5 AND is in Group 6

In Venn diagrams it is possible to have one circle inside another. G is

In Venn diagrams it is possible to have one circle inside another. G is in Group 6 G is not in Group 5

In Venn diagrams it is possible to have one circle inside another. of the

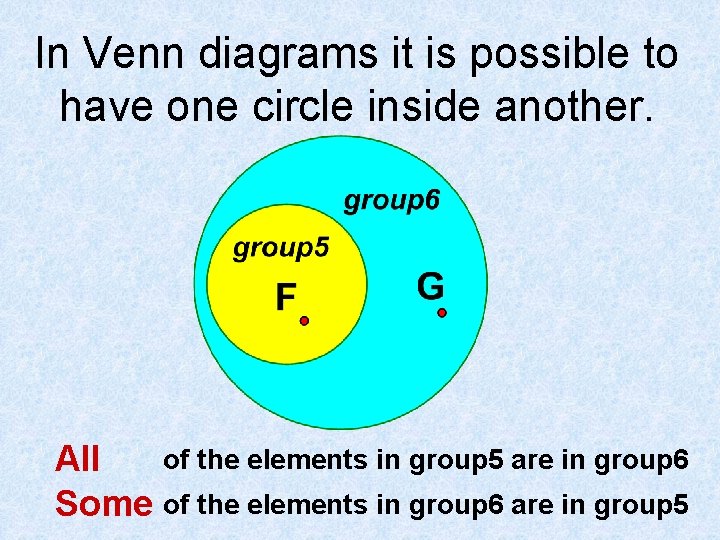
In Venn diagrams it is possible to have one circle inside another. of the elements in group 5 are in group 6 All Some of the elements in group 6 are in group 5

All right angles are congruent. If two angles are right angles, then they are

All right angles are congruent. If two angles are right angles, then they are congruent angles right angles

Every rose is a flower. If you have a rose, then you have a

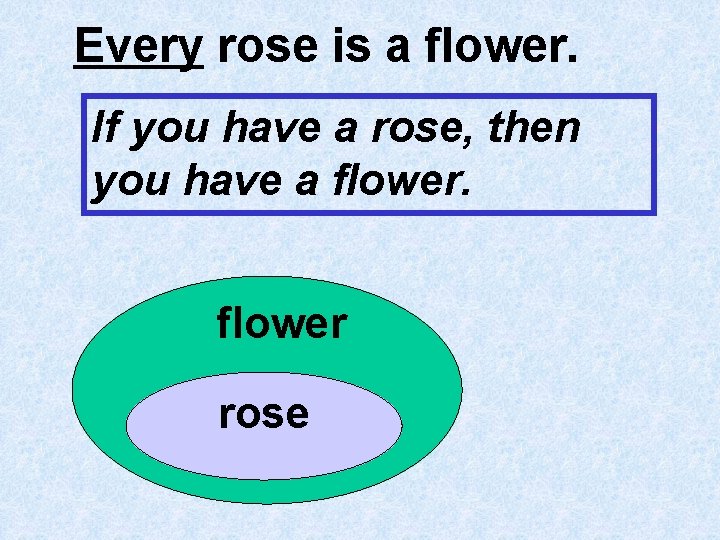
Every rose is a flower. If you have a rose, then you have a flower rose

If two lines are parallel, then they do not intersect. Lines that do not

If two lines are parallel, then they do not intersect. Lines that do not intersect parallel lines

Let’s see how this works! Suppose you are given. . . Twenty-four members of

Let’s see how this works! Suppose you are given. . . Twenty-four members of Mu Alpha Theta went to a Mathematics conference. One -third of the members ran cross country. One sixth of the members were on the football team. Three members were on cross country and football teams. The rest of the members were in the band. How many were in the band?

Use a Venn Diagram and take one sentence at a time. . . •

Use a Venn Diagram and take one sentence at a time. . . • Three members were on cross country and football teams… • Tells you two draw overlapping circles • Put 3 marks in CC F

Use a Venn Diagram and take one sentence at a time. . . •

Use a Venn Diagram and take one sentence at a time. . . • One-third of the members ran cross country. • put 8 marks in the CC circle since there are 24 members • already 3 marks • so put 5 marks in the red part

Use a Venn Diagram and take one sentence at a time. . . •

Use a Venn Diagram and take one sentence at a time. . . • One sixth of the members were on the football team. • put 4 marks in the Football circle since there are 24 members • already 3 marks • so put 1 mark IIIII in the purple part

Use a Venn Diagram and take one sentence at a time. . . •

Use a Venn Diagram and take one sentence at a time. . . • The rest of the members were in the band. How many were in the band? • Out of 24 members in Mu Alpha Theta, 9 play football or run cross country • 15 members are in band

Drawing and Supporting Conclusions

Drawing and Supporting Conclusions

Law of Detachment You are given: a true conditional statement and the hypothesis occurs

Law of Detachment You are given: a true conditional statement and the hypothesis occurs You can conclude: that the conclusion will also occur

Law of Detachment You are given: p q is true p is given Symbolic

Law of Detachment You are given: p q is true p is given Symbolic form You can conclude: q is true

Law of Detachment Example You are given: If three points are collinear, then the

Law of Detachment Example You are given: If three points are collinear, then the points are all on one line. E, F, and G are collinear. You can conclude: E, F, and G are all on one line.

Law of Syllogism You are given: Two true conditional statements and the conclusion of

Law of Syllogism You are given: Two true conditional statements and the conclusion of the first is the hypothesis of the second. You can conclude: that if the hypothesis of the first occurs, then the conclusion of the second will also occur

Law of Syllogism You are given: p q and q r Symbolic form You

Law of Syllogism You are given: p q and q r Symbolic form You can conclude: p r

Law of Syllogism You are given: Example If it rains today, then we will

Law of Syllogism You are given: Example If it rains today, then we will not have a picnic. If we do not have a picnic, then we will not see our friends. You can conclude: If it rains today, then we will not see our friends.

Series of Conditionals The law of syllogism can be applied to a series of

Series of Conditionals The law of syllogism can be applied to a series of statements. Simply reorder statements.

You may need to use contrapositives, since they are logical equivalents to the original

You may need to use contrapositives, since they are logical equivalents to the original statement. This means 1) ~s t is the same as ~t s 2) s r is the same as ~r ~s 3) r ~q is the same as q ~r

EXAMPLE: if p q, s r, ~s t, and r ~q; then p ______?

EXAMPLE: if p q, s r, ~s t, and r ~q; then p ______? You might need the contrapositives: ~t s or ~r ~s or q ~r Start with p and use the law of syllogism to find the conclusion: p q … q ~r … ~r ~s … ~s t p t

VENN DIAGRAMS Venn Diagrams A Venn diagram isVENN DIAGRAMS Venn Diagrams A Venn diagram is
Venn Diagrams John Venn Invented Venn diagrams asVenn Diagrams John Venn Invented Venn diagrams as
Logic and Venn Diagrams Presentation 1 Venn DiagramsLogic and Venn Diagrams Presentation 1 Venn Diagrams
Venn Diagrams and Sets Venn Diagrams One wayVenn Diagrams and Sets Venn Diagrams One way
INTRODUCTION TO VENN DIAGRAMS Introduction to Venn DiagramsINTRODUCTION TO VENN DIAGRAMS Introduction to Venn Diagrams
Chapter 16 Venn Diagrams Venn Diagrams pp 159Chapter 16 Venn Diagrams Venn Diagrams pp 159
Applications of Venn Diagrams Objectives Use Venn diagramsApplications of Venn Diagrams Objectives Use Venn diagrams
Applications of Venn Diagrams Objectives Use Venn diagramsApplications of Venn Diagrams Objectives Use Venn diagrams
Venn Diagrams 1110 I Venn Diagrams with TwoVenn Diagrams 1110 I Venn Diagrams with Two
Venn Diagrams January 2022 Venn Diagrams A setVenn Diagrams January 2022 Venn Diagrams A set
Logic Lesson 2 2 Logic 1 Venn diagramsLogic Lesson 2 2 Logic 1 Venn diagrams
S 1 PROBABILITY Venn Diagrams and Terminology VennS 1 PROBABILITY Venn Diagrams and Terminology Venn
GCSE Venn Diagrams Skipton Girls High School VennGCSE Venn Diagrams Skipton Girls High School Venn
Probability JP Venn Diagrams A Venn diagram isProbability JP Venn Diagrams A Venn diagram is
VENN DIAGRAMS A VENN DIAGRAM IS USED TOVENN DIAGRAMS A VENN DIAGRAM IS USED TO
Lesson 2 2 A Logic Venn Diagrams 5Lesson 2 2 A Logic Venn Diagrams 5
Sample Spaces Venn Diagrams Tree Diagrams and TwoWaySample Spaces Venn Diagrams Tree Diagrams and TwoWay
Unit 10 Logic and Venn Diagrams Presentation 1Unit 10 Logic and Venn Diagrams Presentation 1
Unit 10 Logic and Venn Diagrams Presentation 1Unit 10 Logic and Venn Diagrams Presentation 1
Unit 10 Logic and Venn Diagrams Presentation 1Unit 10 Logic and Venn Diagrams Presentation 1
You used logic and Venn diagrams to determineYou used logic and Venn diagrams to determine
Logic and Logic Programming Logic Propositional Logic FirstLogic and Logic Programming Logic Propositional Logic First
Todays Topics Introduction to Predicate Logic Venn DiagramsTodays Topics Introduction to Predicate Logic Venn Diagrams
Sequence Diagrams Sequence Diagrams Related Terms Interaction DiagramsSequence Diagrams Sequence Diagrams Related Terms Interaction Diagrams