The retarded potentials LL 2 Section 62 Potentials







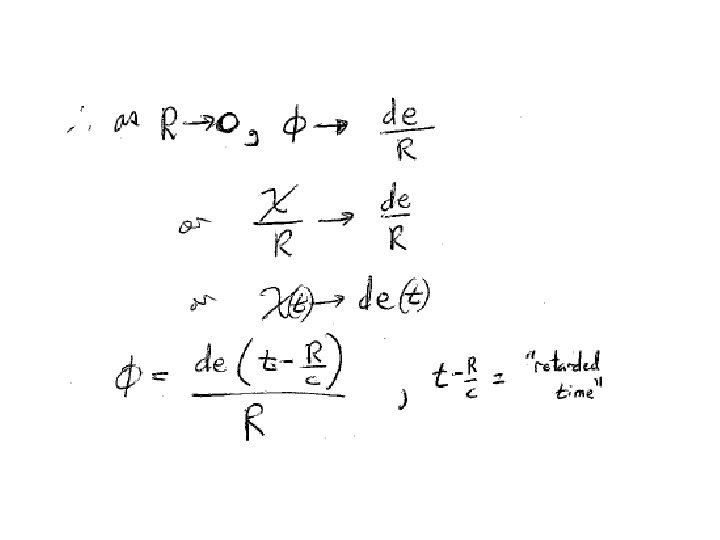


- Slides: 17

The retarded potentials LL 2 Section 62

Potentials for arbitrarily moving charges 2 nd pair of Maxwell’s equations (30. 2) in 4 -D

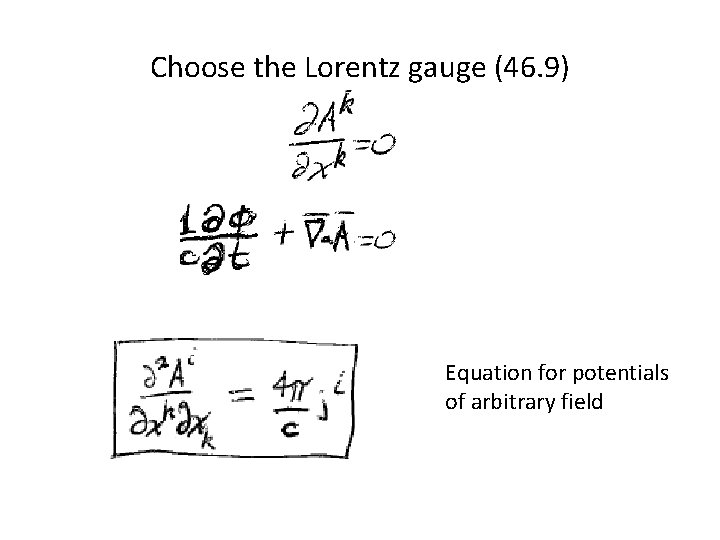
Choose the Lorentz gauge (46. 9) Equation for potentials of arbitrary field

3 D form Space Components: Time Components: If fields are constant, we get Poisson equations (36. 4) & (43. 4) If there are no charges, we get the homogeneous wave equation (46. 7) d’Alembertian operator

Solution to inhomogeneous equation = solution to homogeneous equation + particular solution Recipe 1. Divide space into infinitesimal volume elements 2. Find field due to charges in each element 3. The total field is the linear superposition of the fields from all elements

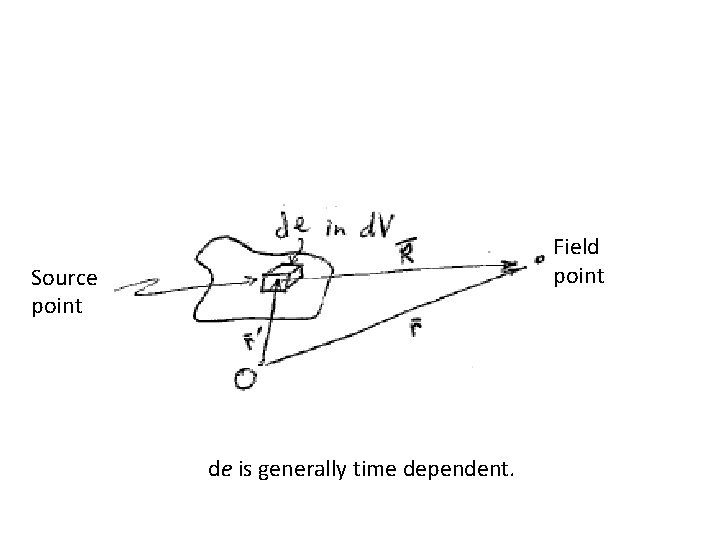
Field point Source point de is generally time dependent.

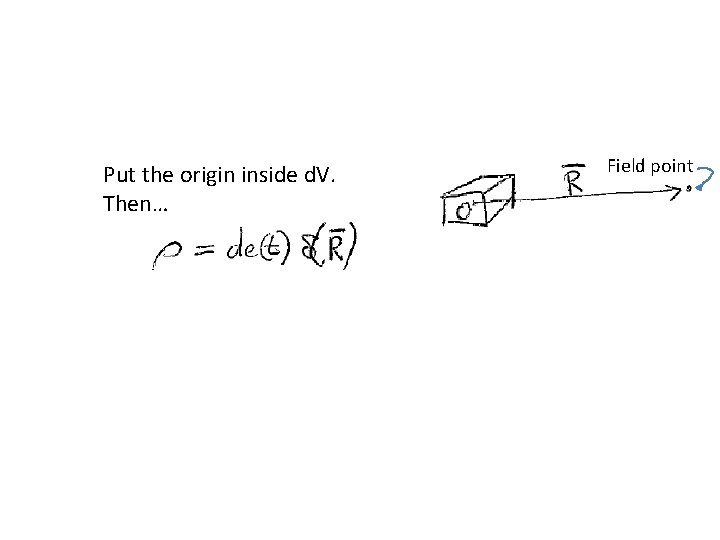
Put the origin inside d. V. Then… Field point

Equation for the scalar potential Everywhere but at the origin we have The problem is centrally symmetric

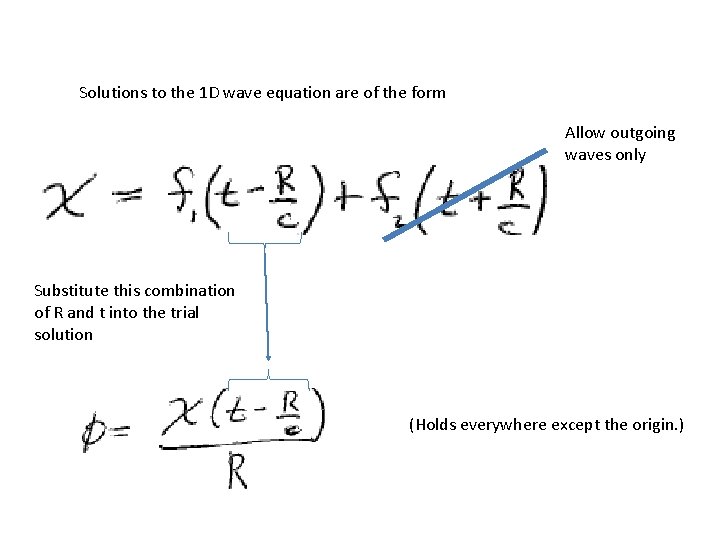
Use spherical coordinates Away from the origin Trial solution (HW) 1 D wave equation

Solutions to the 1 D wave equation are of the form Allow outgoing waves only Substitute this combination of R and t into the trial solution (Holds everywhere except the origin. )

Now determine c to match the potential at the origin Df increases more rapidly than as R goes to zero. Neglect the time derivative We already know the solution to this from Coulomb’s law (36. 9)
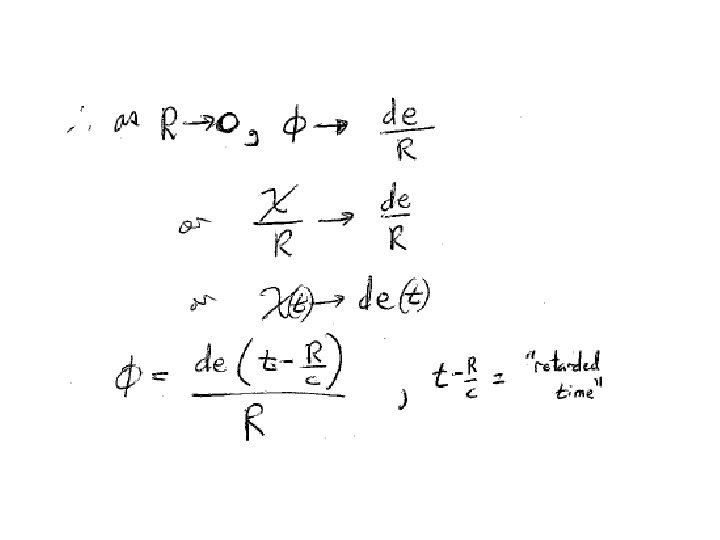

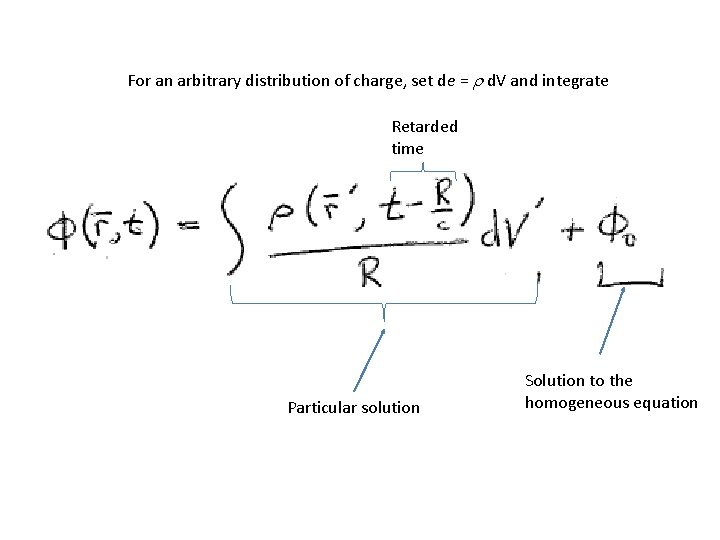
For an arbitrary distribution of charge, set de = r d. V and integrate Retarded time Particular solution Solution to the homogeneous equation

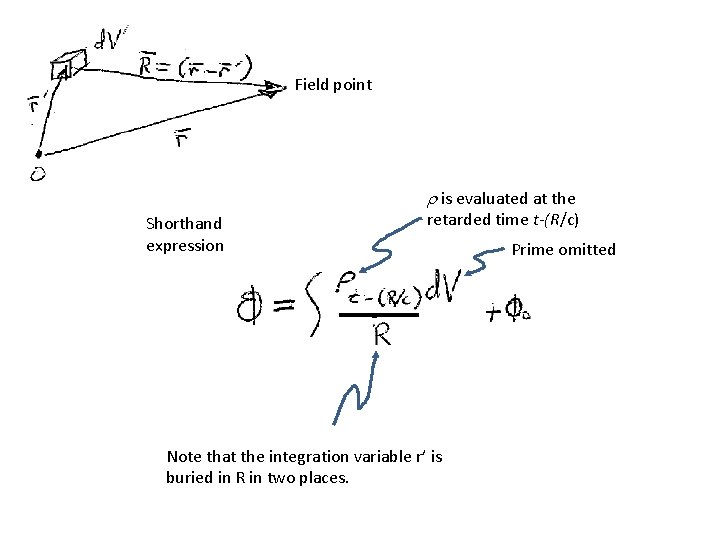
Field point r is evaluated at the Shorthand expression retarded time t-(R/c) Note that the integration variable r’ is buried in R in two places. Prime omitted

Same method for vector potential Retarded potential Solution of homogeneous equation

If charges are stationary, scalar potential should reduce to usual result (36. 8) for constant E-field + f 0 If currents are stationary, vector potential should reduce to usual result (43. 5) for constant H-field + A 0 <A>t =

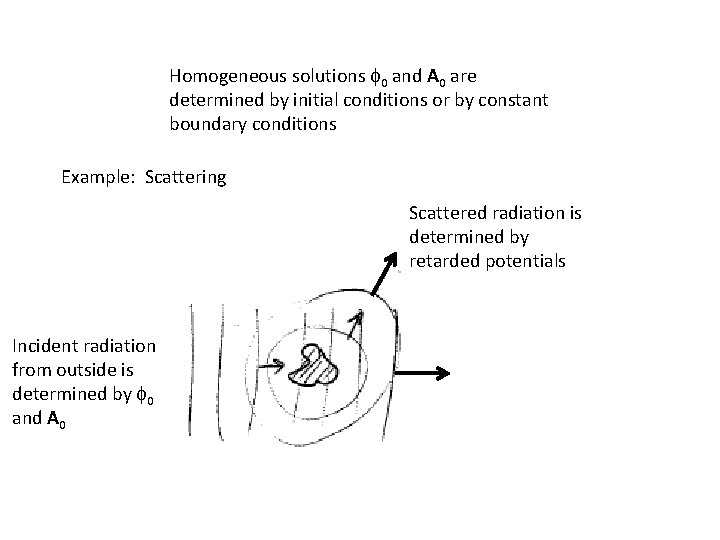
Homogeneous solutions f 0 and A 0 are determined by initial conditions or by constant boundary conditions Example: Scattering Scattered radiation is determined by retarded potentials Incident radiation from outside is determined by f 0 and A 0
 Eθcell
Eθcell Source of bioelectric potential is dash in nature
Source of bioelectric potential is dash in nature Maxwell relations
Maxwell relations Standard reduction potential table
Standard reduction potential table Use the tabulated half-cell potentials to calculate
Use the tabulated half-cell potentials to calculate Graded potential and action potential
Graded potential and action potential Measurable quantities
Measurable quantities Lienard-wiechert potentials
Lienard-wiechert potentials What are electrical synapses
What are electrical synapses Graded vs action potential
Graded vs action potential Scalar magnetic potential
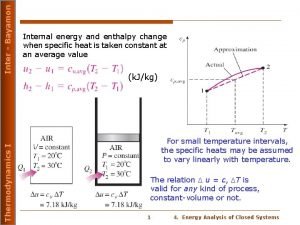
Scalar magnetic potential Difference between internal energy and enthalpy
Difference between internal energy and enthalpy Cathode anode standard reduction potential
Cathode anode standard reduction potential Difference between ipsp and epsp
Difference between ipsp and epsp Explain helmholtz electrical double layer
Explain helmholtz electrical double layer Postsynaptic potentials
Postsynaptic potentials Magnitude electric field
Magnitude electric field đại từ thay thế
đại từ thay thế