The Queue ADT Definition A queue is a

The Queue ADT Definition A queue is a restricted list, where all additions occur at one end, the rear, and all removals occur at the other end, the front. This strategy is known as first-in-first-out (FIFO) strategy. Operations (methods) on queues: enqueue (item) dequeue () size () empty () full () front () Inserts item at the rear of the queue Removes the item from the front of the queue Returns the number of items in the queue Returns true if the queue is empty Returns true if the queue is full Returns the item at the front of the queue without removing it from the queue.

The Queue Interface in two versions version 1: version 2: public interface Queue { public interface Queue. Ex { public void enqueue (int item) throws Queue. Full. Exception; public int dequeue() throws Queue. Empty. Exception; public int size(); public boolean empty(); public boolean full(); public int front() throws Queue. Empty. Exception; public void enqueue (int item); public int dequeue(); public int size(); public boolean empty(); public boolean full(); public int front(); } }

The Queue ADT -- an array implementation (version 1) class Queue. ADT implements Queue { final int MAXSIZE = 100; private int size; private int[] queue. ADT; private int front = 0; private int rear = -1; public void enqueue (int number) { rear++; queue. ADT[rear] = number; } public Queue. ADT () { size = MAXSIZE; queue. ADT = new int[size]; } public int dequeue () { int i = queue. ADT[front]; front++; return i; } public Queue. ADT (int inputsize) { size = inputsize; queue. ADT = new int[size]; } public int front () { return queue. ADT[front]; } public boolean empty () { return (rear < front); } public int size () { return (rear + 1 - front); } public boolean full () { return (rear == size - 1); } }

The Queue ADT -- an array implementation (version 2) class Queue. Empty. Exception extends Exception { public void enqueue (int number) throws Queue. Full. Exception { public Queue. Empty. Exception (String message) { if (full()) System. out. println (message); } } throw new Queue. Full. Exception ("The queue is full. "); rear++; class Queue. Full. Exception extends Exception { queue. ADT[rear] = number; public Queue. Full. Exception (String message) { } System. out. println (message); } } public int dequeue () throws Queue. Empty. Exception { class Queue. ADTEx implements Queue. Ex { if (empty()) final int MAXSIZE = 100; throw new Queue. Empty. Exception ("The queue is empty. "); private int size; int i = queue. ADT[front]; private int[] queue. ADT; front++; private int front = 0; return i; private int rear = -1; } public Queue. ADTEx () { size = MAXSIZE; queue. ADT = new int[size]; } public Queue. ADTEx (int inputsize) { size = inputsize; queue. ADT = new int[size]; } public boolean empty () { return (rear < front); } public boolean full () { return (rear == size - 1); } public int front () throws Queue. Empty. Exception { if (empty()) throw new Queue. Empty. Exception ("The queue is empty. "); return queue. ADT[front]; } public int size () { return (rear + 1 - front); } }

Example application of the Queue ADT using version 1 import java. util. Scanner; class Queue. Appl { public static void main (String[] args) throws IOException { Scanner scan = new Scanner (System. in); System. out. print ("Enter queue size: "); int size = scan. next. Int(); Queue. ADT queue = new Queue. ADT(size); int i = 2; while (!queue. full()) { queue. enqueue(i); System. out. println (queue. front() + " is the front element. "); i = i + 2; } System. out. println ("The current queue contains " + queue. size() + " elements. "); while (!queue. empty()) System. out. println (queue. dequeue() + " is dequeued from the queue. "); if (queue. empty()) System. out. println ("The queue is empty. "); else System. out. println ("There are more elements on the queue. "); } }

Example application of the Queue ADT using version 2 import java. util. Scanner; class Queue. Appl. Ex { public static void main (String[] args) throws IOException { Scanner scan = new Scanner (System. in); System. out. print ("Enter queue size: "); int size = scan. next. Int (); Queue. ADTEx queue = new Queue. ADTEx (size); int i = 2; try { for (int j = 1; j <= 7; j++) { queue. enqueue(i); System. out. println (queue. front() + " is the front item. "); i = i + 2; } } catch (Queue. Full. Exception e) { System. out. println ("The queue is full. "); } catch (Queue. Empty. Exception e) { System. out. println ("The queue is empty. "); } System. out. println ("The current queue contains " + queue. size() + " elements. "); try { for (int j = 1; j <= 7; j++) { System. out. println (queue. dequeue() + " dequeued"); } } catch (Queue. Empty. Exception e) { System. out. println ("The queue is empty. "); } } }

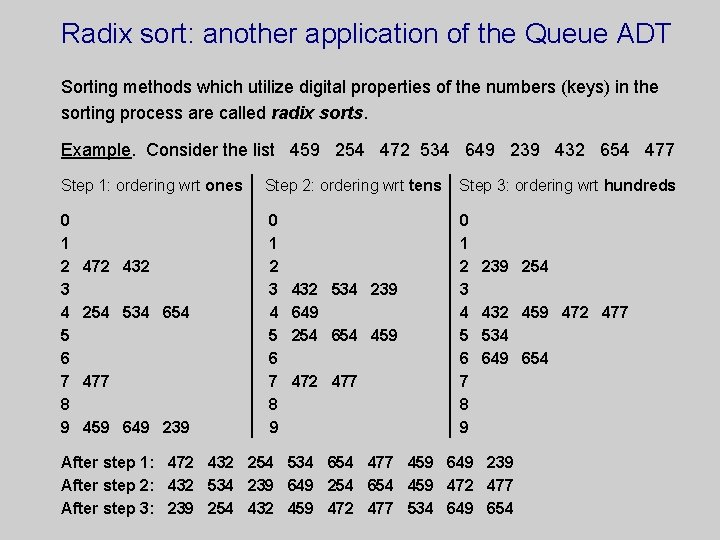
Radix sort: another application of the Queue ADT Sorting methods which utilize digital properties of the numbers (keys) in the sorting process are called radix sorts. Example. Consider the list 459 254 472 534 649 239 432 654 477 Step 1: ordering wrt ones Step 2: ordering wrt tens Step 3: ordering wrt hundreds 0 1 2 3 4 5 6 7 8 9 472 432 254 534 654 477 459 649 239 432 534 239 649 254 654 459 472 477 239 254 432 459 472 477 534 649 654 After step 1: 472 432 254 534 654 477 459 649 239 After step 2: 432 534 239 649 254 654 459 472 477 After step 3: 239 254 432 459 472 477 534 649 654

Radix Sort: the algorithm Consider the following data structures: – a queue for storing the original list and lists resulting from collecting piles at the end of each step (call these master lists); – ten queues for storing piles 0 to 9; Pseudo code description of radix sort at the “idea” level: start with the one’s digit; while there is still a digit on which to classify data do { for each number in the master list do { add that number to the appropriate sublist } for each sublist do { for each number from the sublist do { remove the number from the sublist and append it to a newly arranged master list } } advance the current digit one place to the left }

Radix Sort: the algorithm (cont. ) Here is a more detailed pseudo code description of the radix sort: Input: A queue Q of N items Output: Q sorted in ascending order Algorithm Radix. Sort (Q, N): digit : = 1 while Still. Not. Zero (digit) do { for (i : = 1 to 10) do { create (sublist[i]) } while (! empty Q) do { dequeue (Q, item) pile : = get. Pile (item, digit) + 1 enqueue (sublist[pile], item) } reinitialize (Q) for (j : =1 to 10) do { while (! empty sublist(j)) do { dequeue (sublist[j], item) enqueue (Q, item) } } digit : = digit * 10 } O(N) swaps this outer loop will execute “digit” times

Efficiency of the Radix Sort Operations that affects the efficiency of radix sort the most are “dequeueenqueue” swaps from and to the master list. Because the outer while-loop executes C times, and each of the inner loops is O(N), the total efficiency of radix sort is O(C*N). Notes: 1. If no duplicates are allowed in the list, we have log 10 N <= C for nonnegative integers. 2. If there is a limit on the number of digits in the integers being sorted, we have C <= H * log 10 N. Therefore, radix sort is O(N * log N) algorithm if unique values are sorted; otherwise it is O(N) algorithm with a constant of proportionality, C, which can be large enough to make C * N > N * log. N even for large N. A disadvantage of radix sort is that it required a large amount of memory to keep all of the sub-lists and the master list at the same time.

About the get. Pile method The get. Pile method must return an appropriate isolated digit from the number currently considered. That digit + 1 yields the sublist, where the number is to be enqueued. A possible implementation of the get. Pile method is the following: int get. Pile (int number, int digit) { return (number % (10 * digit) / digit); } Examples: number = 1234 digit = 100 (1234 % 1000) / 100 = 2 number = 12345 digit = 1 (12345 % 10) / 1 = 5