Queue The Queue ADT l l l Insertions

Queue

The Queue ADT l l l Insertions and deletions l follow the first-in first-out scheme l Insertions are at the rear of the queue and removals are at the front of the queue Main queue operations: l enqueue(object): l Auxiliary queue operations: l object front(): returns the element at the front without removing it l integer size(): returns the number of elements stored l boolean is. Empty(): indicates whether no elements are stored inserts an element at the end of the queue l Exceptions l l object dequeue(): l removes and returns the element at the front of the queue Attempting the execution of dequeue or front on an empty queue throws an Queue. Exception

Queue Example Operation enqueue(5) enqueue(3) dequeue() enqueue(7) dequeue() front() dequeue() is. Empty() Output – – 5 – 3 7 7 “error” true Q (5) (5, 3) (3, 7) (7) () () ()

Applications of Queues l l Direct applications l Waiting lists, bureaucracy l Access to shared resources (e. g. , printer) l Multiprogramming Indirect applications l Auxiliary data structure for algorithms l Component of other data structures

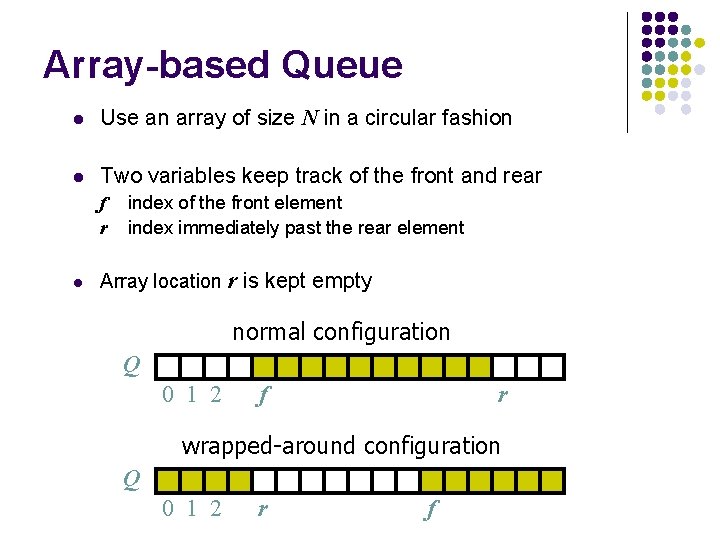
Array-based Queue l Use an array of size N in a circular fashion l Two variables keep track of the front and rear f r l index of the front element index immediately past the rear element Array location r is kept empty normal configuration Q 0 1 2 f r wrapped-around configuration Q 0 1 2 r f

Queue Operations l We use the modulo operator (remainder of division) Algorithm size() return (N f + r) mod N Algorithm is. Empty() return (f = r) Q 0 1 2 f 0 1 2 r r Q f

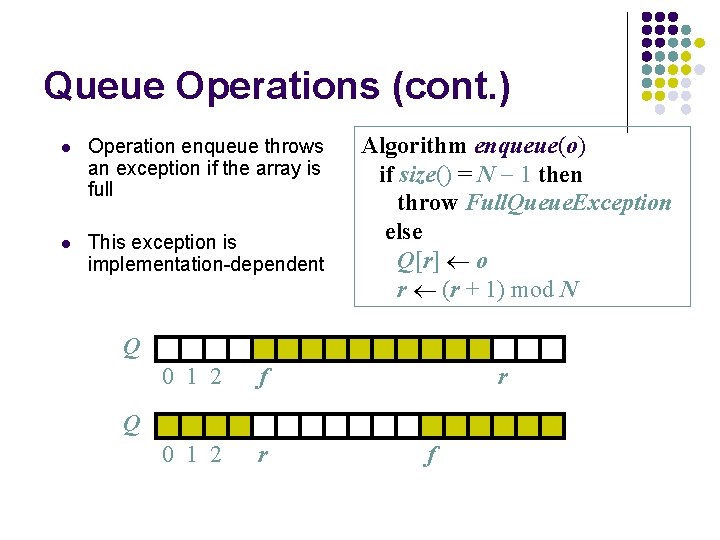
Queue Operations (cont. ) l Operation enqueue throws an exception if the array is full l This exception is implementation-dependent Algorithm enqueue(o) if size() = N 1 then throw Full. Queue. Exception else Q[r] o r (r + 1) mod N Q 0 1 2 f 0 1 2 r r Q f

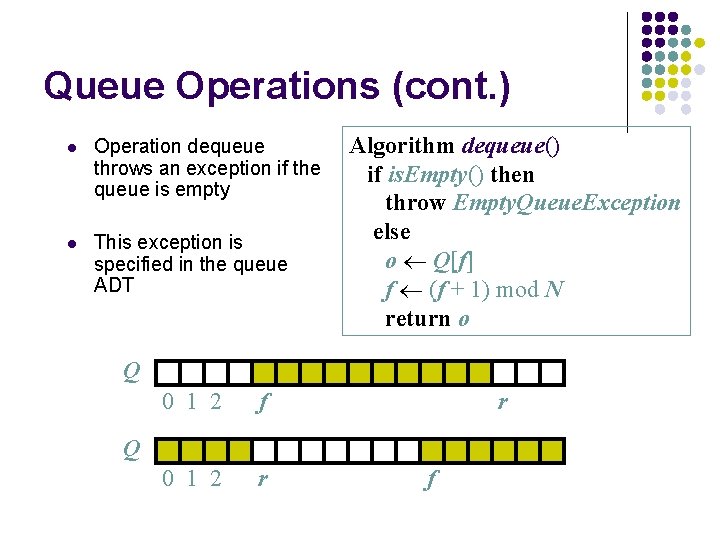
Queue Operations (cont. ) l Operation dequeue throws an exception if the queue is empty l This exception is specified in the queue ADT Algorithm dequeue() if is. Empty() then throw Empty. Queue. Exception else o Q[f] f (f + 1) mod N return o Q 0 1 2 f 0 1 2 r r Q f

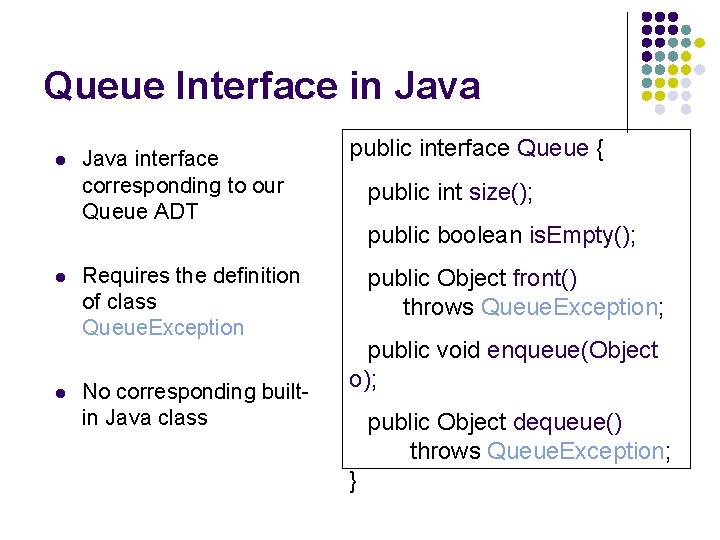
Queue Interface in Java l l l Java interface corresponding to our Queue ADT Requires the definition of class Queue. Exception No corresponding builtin Java class public interface Queue { public int size(); public boolean is. Empty(); public Object front() throws Queue. Exception; public void enqueue(Object o); public Object dequeue() throws Queue. Exception; }

Application: Round Robin Schedulers We can implement a round robin scheduler using a queue, Q, by repeatedly performing the following steps: l 1. 2. 3. e = Q. dequeue() Service element e Q. enqueue(e) The Queue 1. Deque the next element 2. Service the next element Shared Service 3. Enqueue the serviced element

Example: Jospehus Problem l l A group of students passing a “hot potato” around l When the leader rings the bell after potato is passed around k times l l Process continues until a winner is declared Solving the problem given l l l Whoever has the hot potato loses a list of names and a fixed value for k Refer to Josephus. Problem Project