The Product Rule In words Keep the first


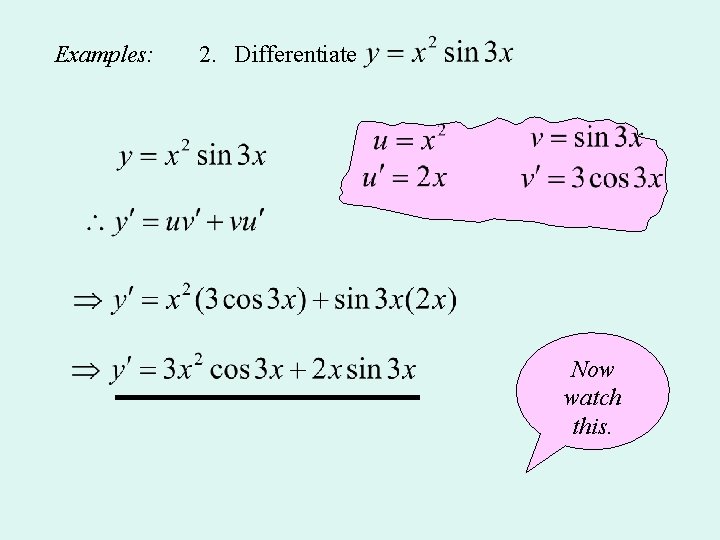

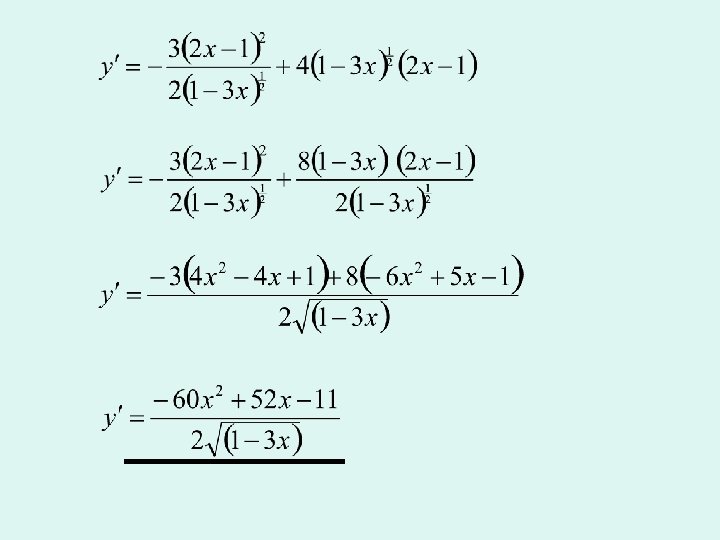

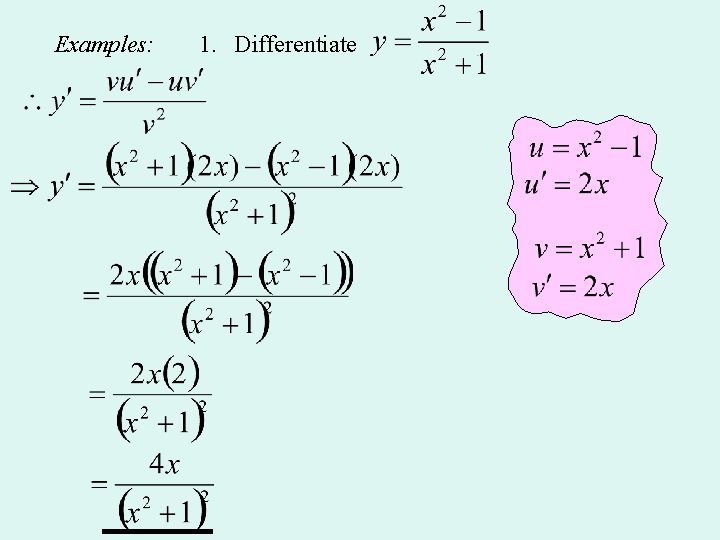





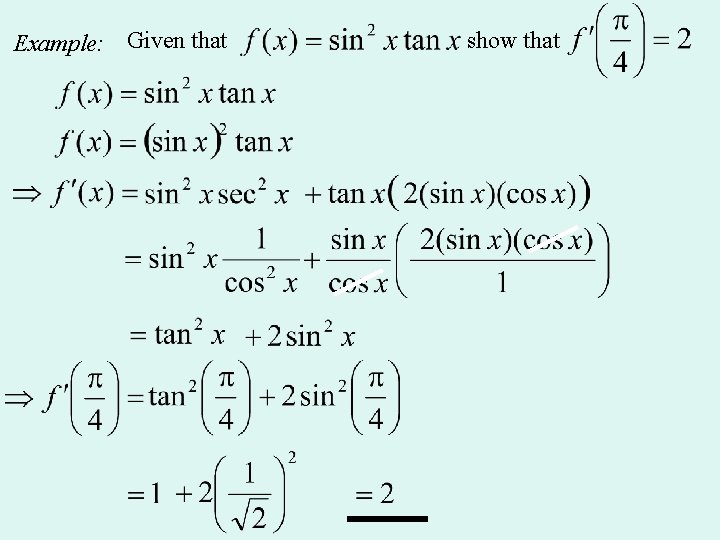








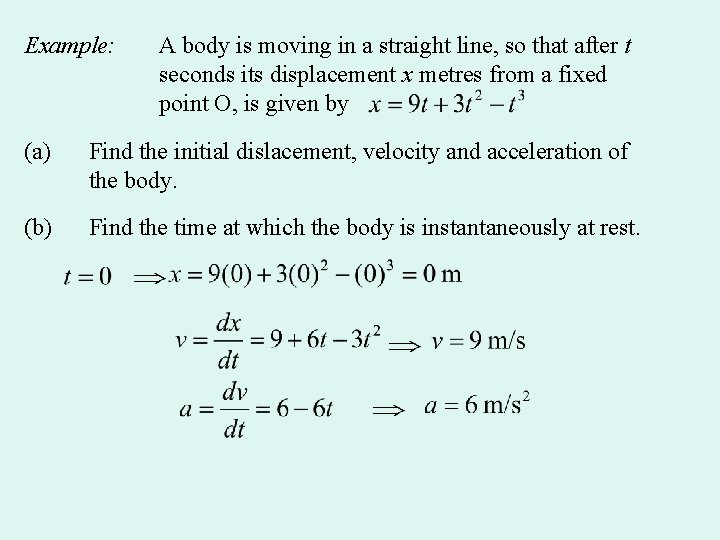




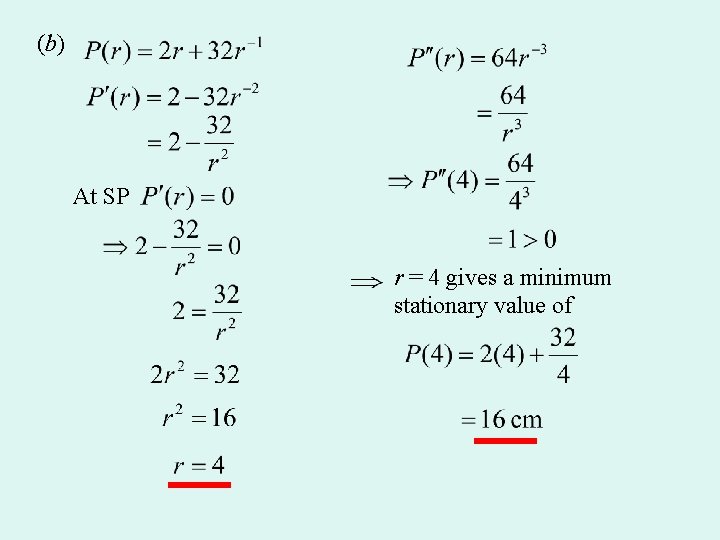
- Slides: 35

The Product Rule In words: “Keep the first, differentiate the second” + “Keep the second, differentiate the first”

Examples: 1. Differentiate
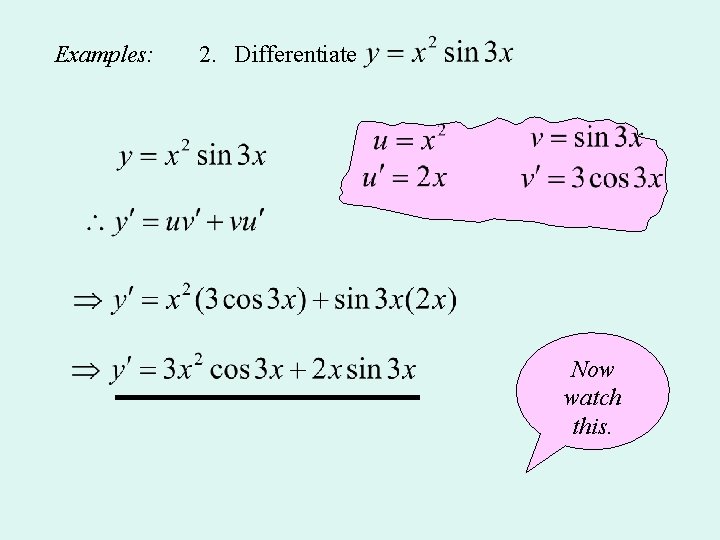
Examples: 2. Differentiate Now watch this.

Examples: 3. Differentiate Try this using “words”
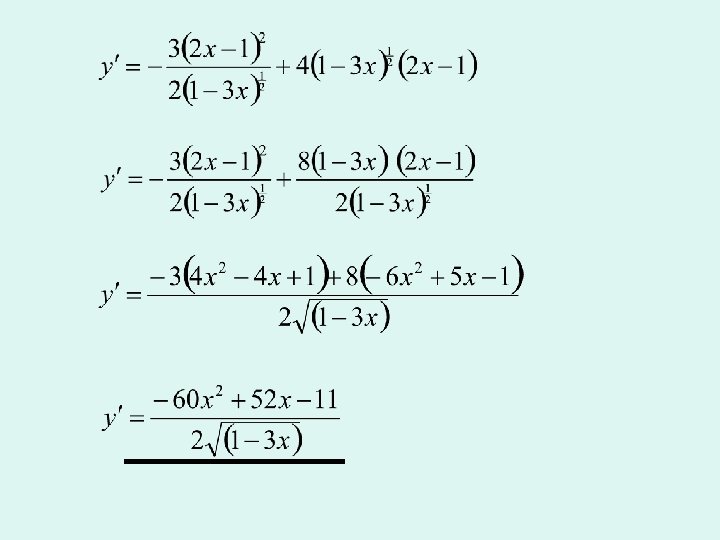

The Quotient Rule In words: “Keep the denominator, – differentiate the numerator” “Keep the numerator, differentiate the denominator” Denominator 2
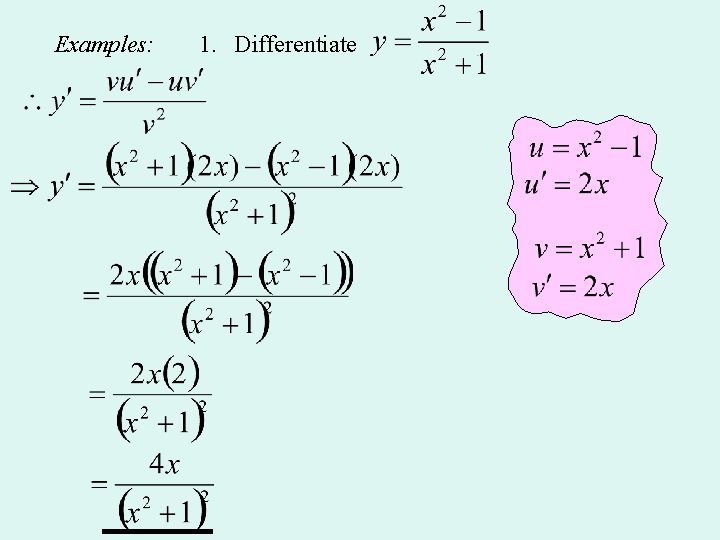
Examples: 1. Differentiate

Examples: 2. Differentiate Try this using “words”

Add a denominator here

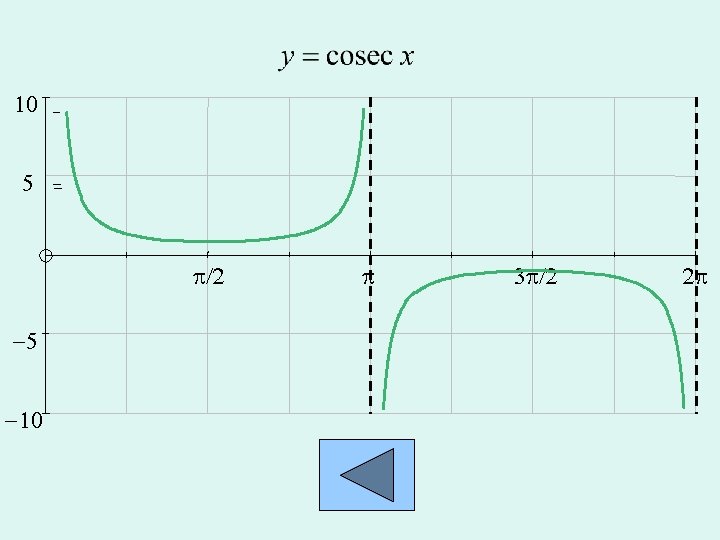
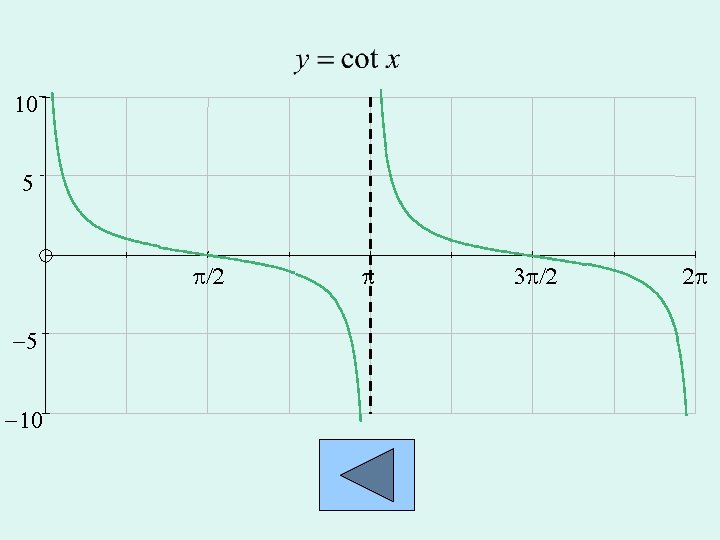
Derivatives of New Functions Definitions: Reminder: continue

10 5 p/2 -5 -10 p 3 p/2 2 p

10 5 p/2 -5 -10 p 3 p/2 2 p

10 5 p/2 -5 -10 p 3 p/2 2 p

Derivative of Proof: Use the Quotient Rule now

Derivatives of Prove these and keep with your notes. Use chain rule or quotient rule
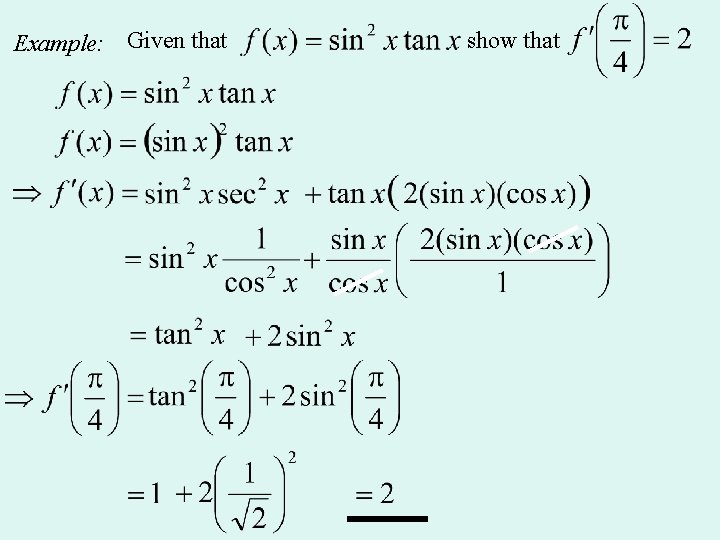
Example: Given that show that

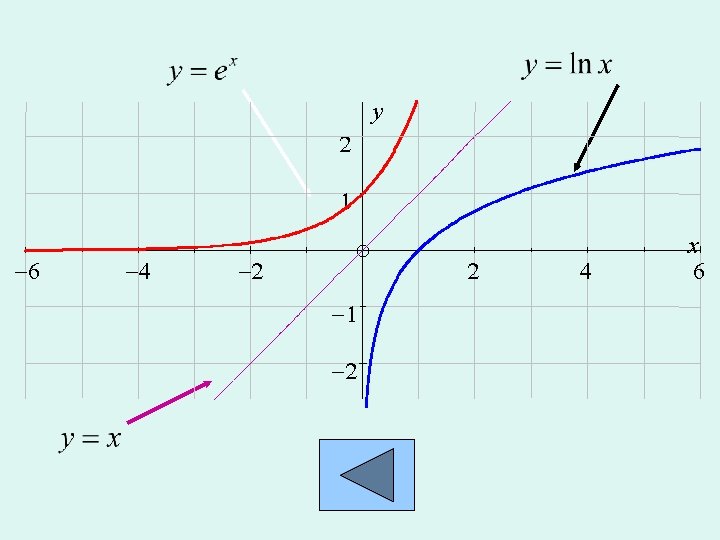
Exponential and Logarithmic Functions and Reminder: are inverse to each other. They are perhaps the most important functions in the applications of calculus in the real world. Alternative notation: Two very useful results: Also: Learn these! Practise changing from exp to log and vice-versa.

y 2 1 -6 -4 -2 2 -1 -2 4 x 6

Derivatives of the Exponential and Logarithmic Functions (i) Proof of (ii)

Examples: 1. Differentiate Use the Chain Rule 2. Differentiate Use the Product Rule

3. Differentiate Use the Chain Rule 4. Differentiate Use the Quotient Rule

Note: In general • • Useful for reverse i. e. INTEGRATION

Higher Derivatives Given that f is differentiable, if then its derivative is denoted by is also differentiable. The two notations are: function f 1 st 2 nd derivative …… …… …… nth derivative

Example: If , write down is first second and third derivatives and hence make a conjecture about its nth derivative. Conjecture: The nth derivative is

Rectilinear Motion If displacement from the origin is a function of time I. e. then v - velocity a - acceleration
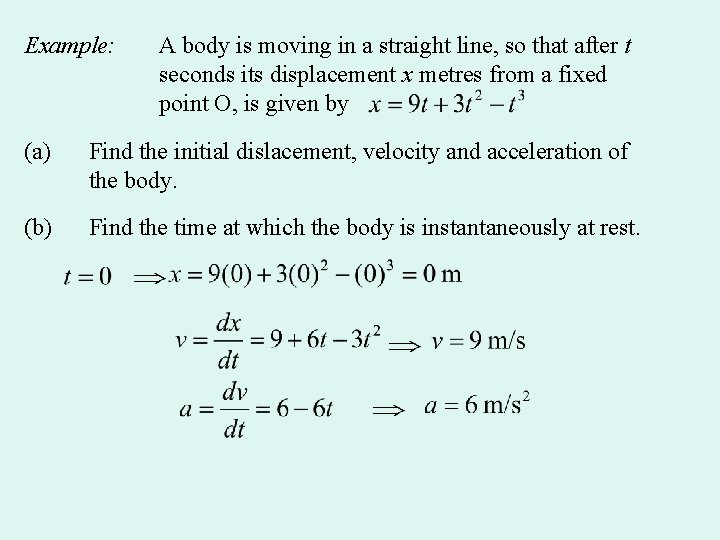
Example: A body is moving in a straight line, so that after t seconds its displacement x metres from a fixed point O, is given by (a) Find the initial dislacement, velocity and acceleration of the body. (b) Find the time at which the body is instantaneously at rest.

Extreme Values of a Function Understand the following terms: • Critical Points • Local Extreme Values § Local maximum § Local minimum • End Point Extreme Values § End Point maximum § End Point minimum See, MIA Mathematics 1, Pages 54 – 55

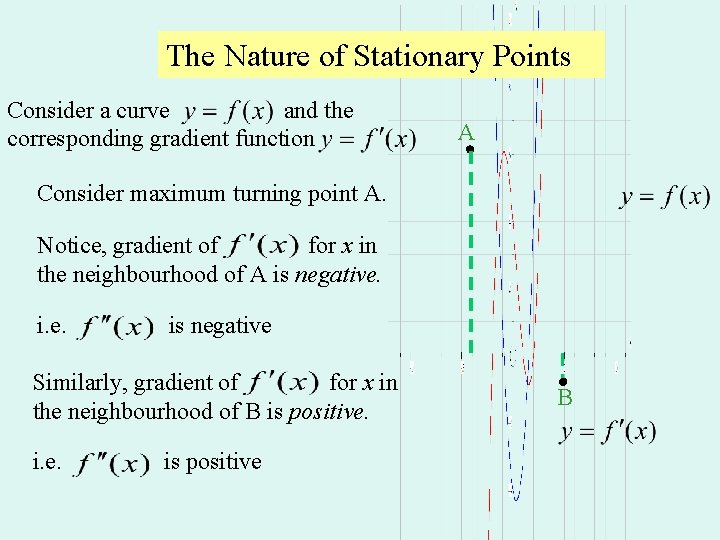
The Nature of Stationary Points Consider a curve and the corresponding gradient function A Consider maximum turning point A. Notice, gradient of for x in the neighbourhood of A is negative. i. e. is negative Similarly, gradient of for x in the neighbourhood of B is positive. i. e. is positive B

The Nature of Stationary Points Rule for Stationary Points • and minimum turning point • and maximum turning point • and possibly a point of inflexion but must check using a table of signs

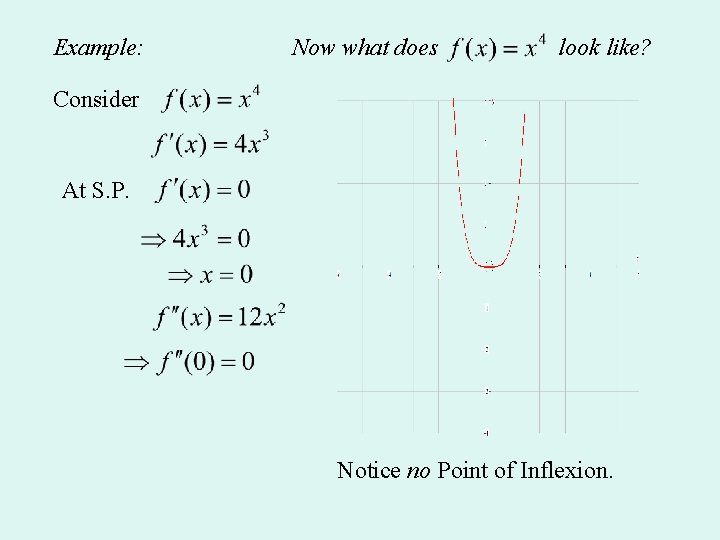
Example: Now what does look like? Consider At S. P. Notice no Point of Inflexion.

Global Extreme Values Understand the following terms: • Global Extreme Values § Global maximum § Global minimum See, MIA Mathematics 1, Pages 58 – 59

Example: Find the coordinates and nature of the stationary point on the curve What does this curve look like? At S. P. is a Minimum Turning Point

y x

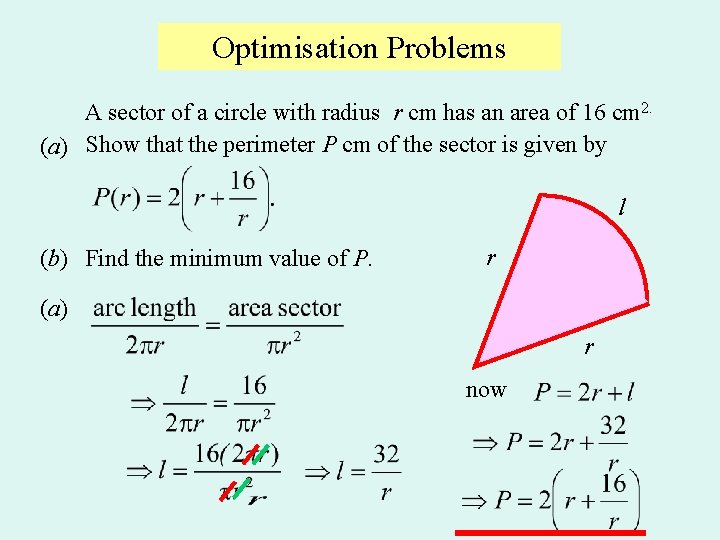
Optimisation Problems A sector of a circle with radius r cm has an area of 16 cm 2. (a) Show that the perimeter P cm of the sector is given by l (b) Find the minimum value of P. r (a) r now
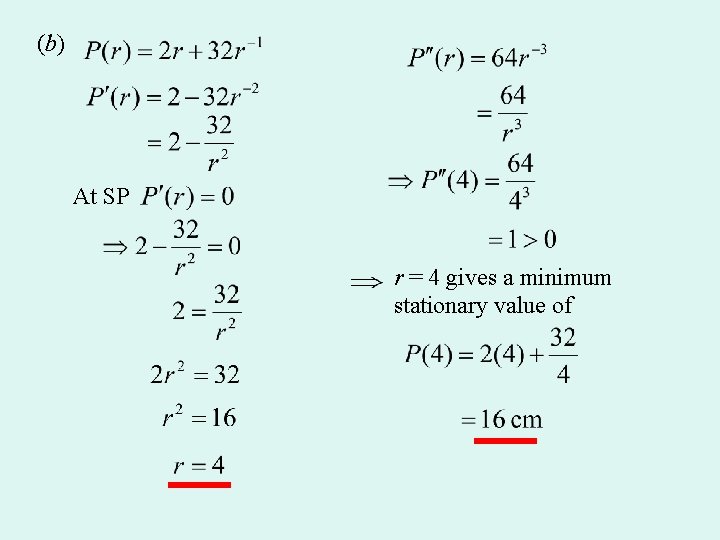
(b) At SP r = 4 gives a minimum stationary value of
 Parents promoters apathetics defenders
Parents promoters apathetics defenders Power interest grid
Power interest grid Keep it secret keep it safe
Keep it secret keep it safe Rule of sum and rule of product
Rule of sum and rule of product What is the cold chain rule
What is the cold chain rule Product rule in differentiation
Product rule in differentiation Special triangles
Special triangles When to use sine rule and cosine rule
When to use sine rule and cosine rule Soh cah toa rules
Soh cah toa rules Kirchhoff's junction rule states that
Kirchhoff's junction rule states that Dillon rule
Dillon rule Kirchhoff's loop rule
Kirchhoff's loop rule With the rule astigmatism
With the rule astigmatism Compound astigmatism example
Compound astigmatism example With the rule astigmatism axis
With the rule astigmatism axis General power rule
General power rule Sine and cosine rules
Sine and cosine rules Chain rule power rule
Chain rule power rule Tukey's rule vs empirical rule
Tukey's rule vs empirical rule Probability product rule
Probability product rule Derivative product rule
Derivative product rule Log a to the power x
Log a to the power x What is the product rule for radicals
What is the product rule for radicals Integration rules
Integration rules Integrate product rule
Integrate product rule Antiderivative of product rule
Antiderivative of product rule Zero factor property
Zero factor property Subtraction rule discrete math
Subtraction rule discrete math Product and quotient rule
Product and quotient rule Differentiation rule for division
Differentiation rule for division Differentiation formulas class 11
Differentiation formulas class 11 Integral of product
Integral of product Product rule differentiation
Product rule differentiation 9-4 solving quadratic equations by factoring
9-4 solving quadratic equations by factoring Integral product rule
Integral product rule Cross product right hand rule
Cross product right hand rule

























































