Section 2 3 The Product and Quotient Rules

Section 2. 3 – The Product and Quotient Rules and Higher-Order Derivatives

The Product Rule The derivative of a product of functions is NOT the product of the derivatives. If f and g are both differentiable, then In other words, the derivative of a product of two functions is the first function times the derivative of the second function plus the second function times the derivative of the first function. Another way to write the Rule:

Example 1 Differentiate the function: u u v v v' Product Rule Sum/Difference Rule Power Rule Simplify u'

Example 2 If h(x) = xg(x) and it is known that g(3) = 5 and g'(3) =2, find h'(3). u v Find the derivative: u v' u Product Rule Evaluate the derivative: v'

The Quotient Rule The derivative of a quotient of functions is NOT the quotient of the derivatives. If f and g are both differentiable, then “Lo-d-Hi minus Hi-d-Lo” In other words, the derivative of a quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. Another way to write the Rule:

Example 1 Differentiate the function: u v v u' u v 2 Quotient Rule v'

Example 2 Find an equation of the tangent line to the curve the point (1, ½). at Find the Derivative Find the derivative (slope of the tangent line) when x=1 Use the point-slope formula to find an equation

Example 3 Differentiate the function: The Quotient Rule is long, don’t forget to rewrite if possible. Rewrite to use the power rule Sum and Difference Rules Constant Multiple Rule Power Rule Try to find the Least Common Denominator Simplify

More Derivatives of Trigonometric Functions We will assume the following to be true:

Example 1 Differentiate the function: Use the Quotient Rule u v v u' u v' Quotient Rule Always look to simplify Trig Law: 1 + tan 2 = sec 2

Example 2 Differentiate the function: u u Use the Product Rule v v' v Product Rule u'

Example 1 Let a. Find the derivative of the function.

Example 1 (Continued) Let b. Find the derivative of the function found in (a).

Example 1 (Continued) Let c. Find the derivative of the function found in (b).

Example 1 (Continued) Let d. Find the derivative of the function found in (c).

Example 1 (Continued) Let e. Find the derivative of the function found in (d). We have just differentiated the derivative of a function. Because the derivative of a function is a function, differentiation can be applied over and over as long as the derivative is a differentiable function.

Higher-Order Derivatives: Notation First Derivative: Second Derivative: Third Derivative: Fourth Derivative: nth Derivative: Notice that for derivatives of higher order than the third, the parentheses distinguish a derivative from a power. For example: .

Example 1 (Continued) Let f. Define the derivatives from (a-e) with the correct notation. You should note that all higher-order derivatives of a polynomial p(x) will also be polynomials, and if p has degree n, then p(n)(x) = 0 for k ≥ n+1.

Example 2 If , find . Will ever equal 0? Find the first derivative: Find the second derivative: Find the third derivative: No higher-order derivative will equal 0 since the power of the function will never be 0. It decreases by one each time.

Example 3 Find the second derivative of Find the first derivative: . Find the second derivative:

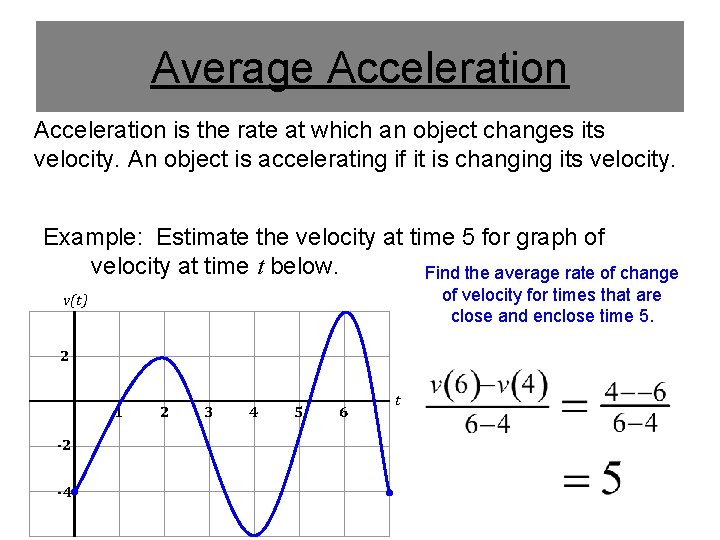
Average Acceleration is the rate at which an object changes its velocity. An object is accelerating if it is changing its velocity. Example: Estimate the velocity at time 5 for graph of velocity at time t below. Find the average rate of change of velocity for times that are close and enclose time 5. v(t) 2 1 -2 -4 2 3 4 5 6 t

Instantaneous Acceleration If s = s(t) is the position function of an object that moves in a straight line, we know that its first derivative represents the velocity v(t) of the object as a function of time. The instantaneous rate of change of velocity with respect to time is called the acceleration a(t) of an object. Thus, the acceleration function is the derivative of the velocity function and is therefore the second derivative of the position function.

Position, Velocity, and Acceleration are related in the following manner: Units = Measure of length (ft, m, km, etc) Position: The object is… Moving right/up when v(t) > 0 Moving left/down when v(t) < 0 Still or changing directions when v(t) = 0 Velocity: Speed = absolute value of v(t) Units = Distance/Time (mph, m/s, ft/hr, etc) Acceleration: Units = (Distance/Time)/Time (m/s 2)

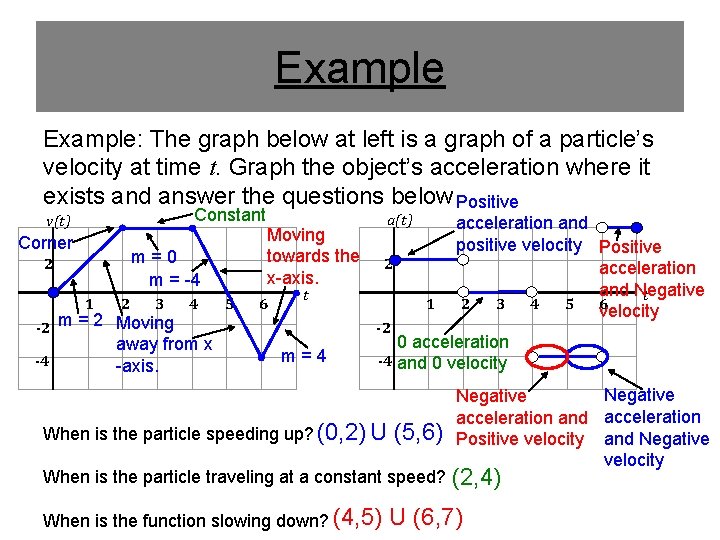
Example: The graph below at left is a graph of a particle’s velocity at time t. Graph the object’s acceleration where it exists and answer the questions below Positive Constant v(t) Corner m=0 m = -4 2 1 2 3 -2 m = 2 Moving -4 4 away from x -axis. 5 a(t) Moving towards the x-axis. 6 2 t 1 -2 m=4 acceleration and positive velocity Positive acceleration and Negative t 2 3 4 5 6 velocity 0 acceleration -4 and 0 velocity When is the particle speeding up? (0, 2) U (5, 6) When is the particle traveling at a constant speed? When is the function slowing down? (4, 5) Negative acceleration and acceleration Positive velocity and Negative velocity (2, 4) U (6, 7)

Speeding Up and Slowing Down An object is SPEEDING UP when the following occur: • Algebraic: If the velocity and the acceleration agree in sign • Graphical: If the curve is moving AWAY from the x-axis An object is traveling at a CONSTANT SPEED when the following occur: • Algebraic: Velocity is constant and acceleration is 0. • Graphically: The velocity curve is horizontal An object is SLOWING DOWN when the following occur: • Algebraic: Velocity and acceleration disagree in sign • Graphically: The velocity curve is moving towards the xaxis

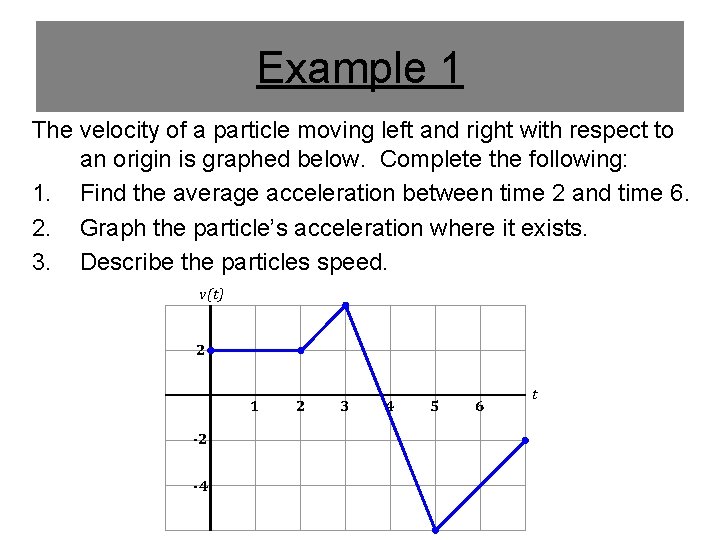
Example 1 The velocity of a particle moving left and right with respect to an origin is graphed below. Complete the following: 1. Find the average acceleration between time 2 and time 6. 2. Graph the particle’s acceleration where it exists. 3. Describe the particles speed. v(t) 2 1 -2 -4 2 3 4 5 6 t

Example 2 Sketch a graph of the function that describes the velocity of a particle moving up and down with the following characteristics: The particle’s velocity is defined on [0, 8] The particle is only slowing down on (1, 3)U(4, 7) The acceleration is never 0.

Example 3 The position of a particle is given by the equation where t is measured in seconds and s in meters. (a) Find the acceleration at time t. The derivative of the position function is the velocity function. The derivative of the velocity function is the acceleration function.

Example 3 (continued) The position of a particle is given by the equation where t is measured in seconds and s in meters. (b) What is the acceleration after 4 seconds? m/s 2 (c) Is the particle speeding up, slowing down, or traveling at a constant speed at 4 seconds? Since the velocity and m/s 2 acceleration agree in signs, the particle is speeding up.

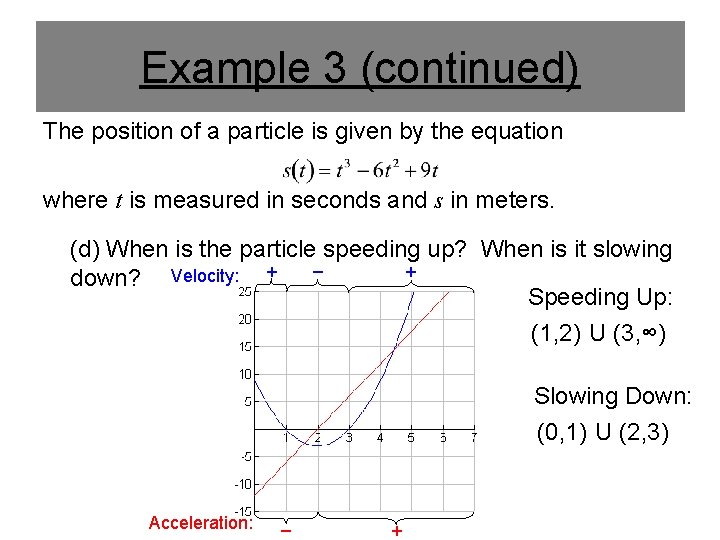
Example 3 (continued) The position of a particle is given by the equation where t is measured in seconds and s in meters. (d) When is the particle speeding up? When is it slowing – + down? Velocity: + Speeding Up: (1, 2) U (3, ∞) Slowing Down: (0, 1) U (2, 3) Acceleration: – +