TECNOLOGIE INFORMATICHE NELLA DIDATTICA Applicate alle discipline Matematica

TECNOLOGIE INFORMATICHE NELLA DIDATTICA Applicate alle discipline Matematica Fisica Grafica pubblicitaria

CABRI GEOMETRE Software dinamico per la didattica MATEMATICA FISICA GRAFICA PUBBLICITARIA

FORMAZIONE DOCENTI A TEMPO INDETERMINATO DI NUOVA ASSUNZIONE Anno Scolastico 2004/2005 DIRETTORE DEL CORSO: Prof. Giovanni Vassallo TUTOR: Prof. Salvatore Cavallaro UTILIZZO DI CABRI GEOMETRE PER OTTENERE SOLUZIONI APPROSSIMATE DI EQUAZIONI POLINOMIALI IN UNA INCOGNITA, DI QUALSIASI GRADO (CON UNA PIU’ APPROFONDITA ANALISI DEL CASO POLINOMI DI SECONDO GRADO)

Dal Polinomio alla Spezzata: • Ad un polinomio di secondo grado nella sola incognita “X” è possibile associare su un piano cartesiano “Oxy” una spezzata che comincia dal punto O ed è costituita da 3 segmenti incidenti ad angolo retto • Ad ogni polinomio nella sola incognita “X” è possibile associare su un piano cartesiano “Oxy” una spezzata che comincia dall’origine O e costituita da tanti segmenti quanto il grado del polinomio più 1.

P(X) = AX² + BX + C La spezzata associata al polinomio si può interpretare come il cammino di un pedone su una scacchiera: il pedone si muove da principio lungo l’asse X di esattamente A quadretti in avanti (è sempre possibile fare in modo che A sia un numero positivo);

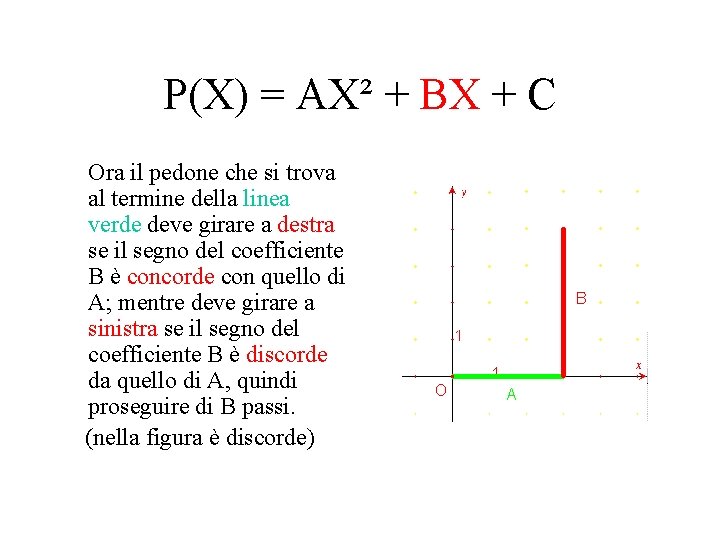
P(X) = AX² + BX + C Ora il pedone che si trova al termine della linea verde deve girare a destra se il segno del coefficiente B è concorde con quello di A; mentre deve girare a sinistra se il segno del coefficiente B è discorde da quello di A, quindi proseguire di B passi. (nella figura è discorde)

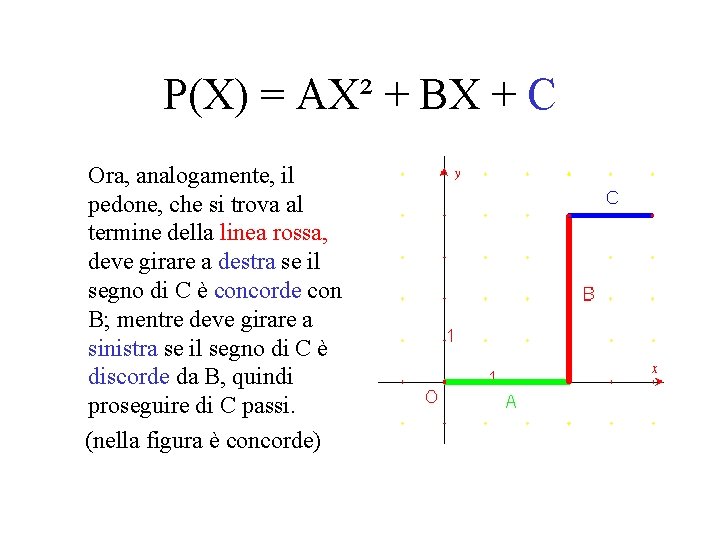
P(X) = AX² + BX + C Ora, analogamente, il pedone, che si trova al termine della linea rossa, deve girare a destra se il segno di C è concorde con B; mentre deve girare a sinistra se il segno di C è discorde da B, quindi proseguire di C passi. (nella figura è concorde)

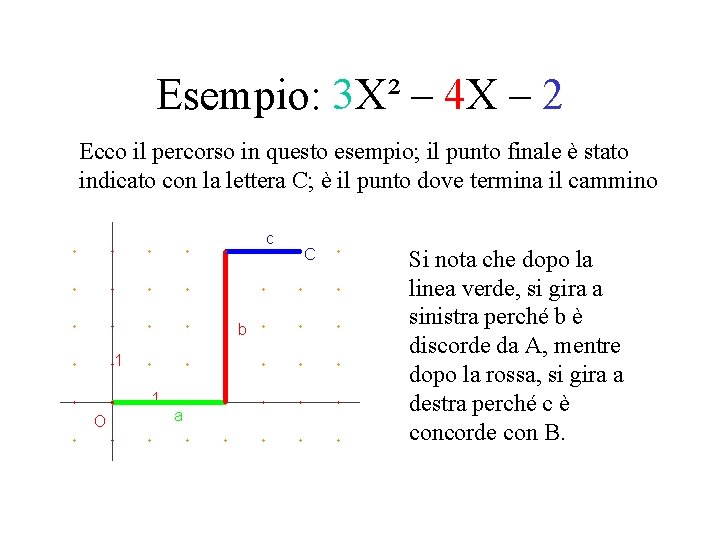
Esempio: 3 X² – 4 X – 2 Ecco il percorso in questo esempio; il punto finale è stato indicato con la lettera C; è il punto dove termina il cammino Si nota che dopo la linea verde, si gira a sinistra perché b è discorde da A, mentre dopo la rossa, si gira a destra perché c è concorde con B.

Caso generale e considerazioni. Nel caso generale, un polinomio di grado N, avrà N+1 coefficienti (si contano anche quelli eventualmente nulli, ), a cui è possibile associare una spezzata che avrà N+1 segmenti, il procedimento è esattamente uguale a quello del caso quadratico. Considerazione particolare deve avere il caso dove uno o più coefficienti sono nulli, in quanto il pedone non avanza, ma si gira solamente e si prepara al tratto successivo, in che modo? E’ indifferente se si considera lo 0 un numero positivo o negativo, basta scegliere un’opzione e comportarsi di conseguenza…

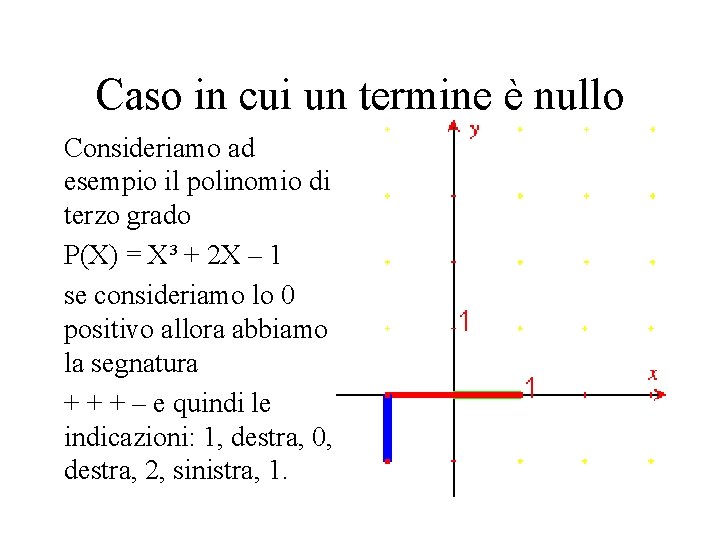
Caso in cui un termine è nullo Consideriamo ad esempio il polinomio di terzo grado P(X) = X³ + 2 X – 1 se consideriamo lo 0 positivo allora abbiamo la segnatura + + + – e quindi le indicazioni: 1, destra, 0, destra, 2, sinistra, 1.

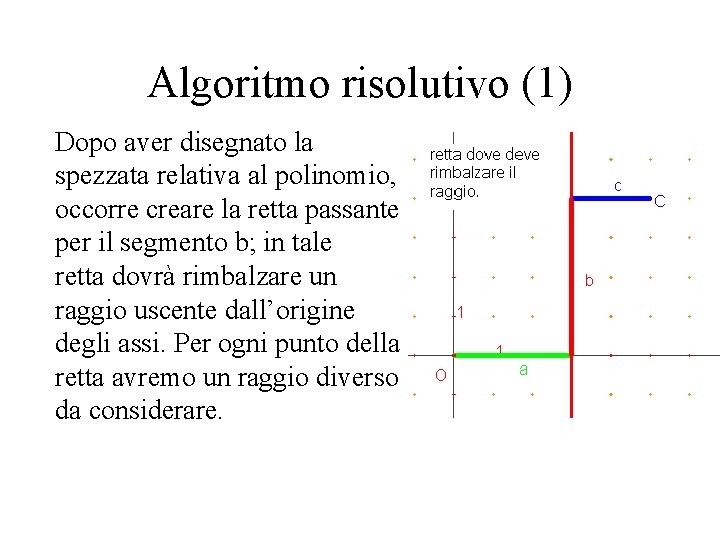
Algoritmo risolutivo (1) Dopo aver disegnato la spezzata relativa al polinomio, occorre creare la retta passante per il segmento b; in tale retta dovrà rimbalzare un raggio uscente dall’origine degli assi. Per ogni punto della retta avremo un raggio diverso da considerare.

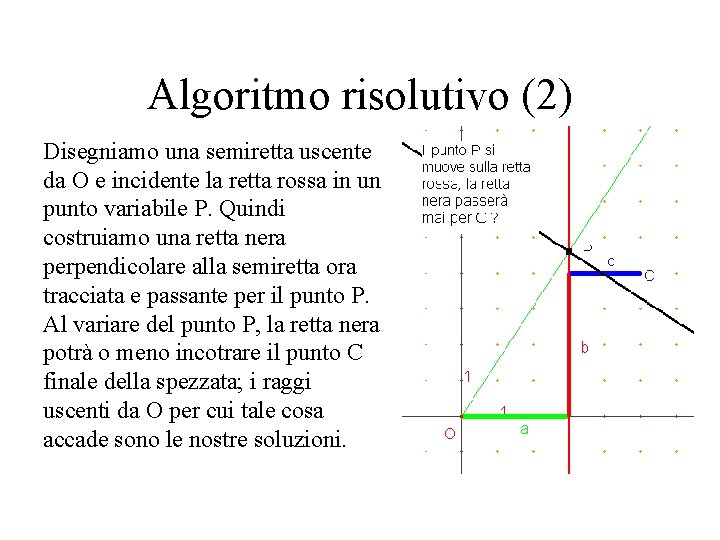
Algoritmo risolutivo (2) Disegniamo una semiretta uscente da O e incidente la retta rossa in un punto variabile P. Quindi costruiamo una retta nera perpendicolare alla semiretta ora tracciata e passante per il punto P. Al variare del punto P, la retta nera potrà o meno incotrare il punto C finale della spezzata; i raggi uscenti da O per cui tale cosa accade sono le nostre soluzioni.

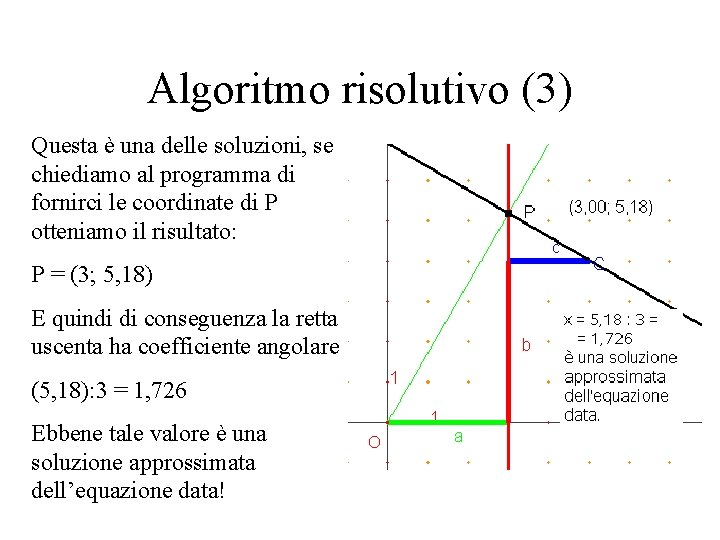
Algoritmo risolutivo (3) Questa è una delle soluzioni, se chiediamo al programma di fornirci le coordinate di P otteniamo il risultato: P = (3; 5, 18) E quindi di conseguenza la retta uscenta ha coefficiente angolare (5, 18): 3 = 1, 726 Ebbene tale valore è una soluzione approssimata dell’equazione data!

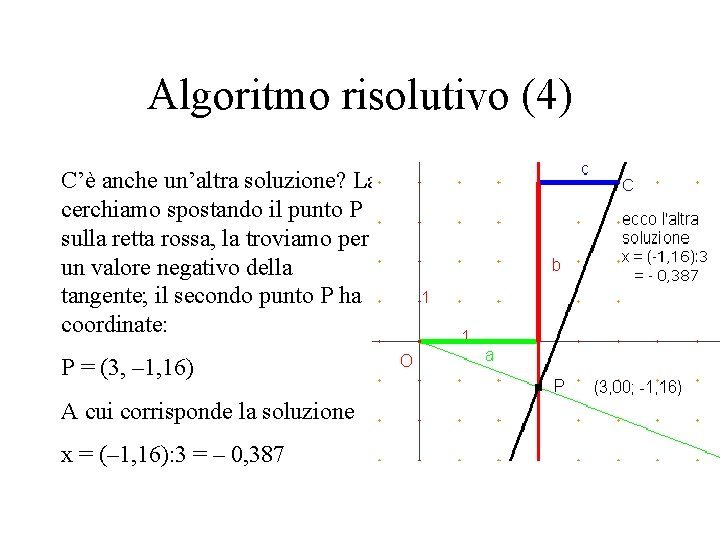
Algoritmo risolutivo (4) C’è anche un’altra soluzione? La cerchiamo spostando il punto P sulla retta rossa, la troviamo per un valore negativo della tangente; il secondo punto P ha coordinate: P = (3, – 1, 16) A cui corrisponde la soluzione x = (– 1, 16): 3 = – 0, 387

Commento dei risultati Verifichiamo la bontà dei risultati ottenuti, confrontandoli con i veri risultati forniti dalla formula risolutiva: Abbiamo Delta = 16+24= 30 E quindi x 1 = 1, 579 ; x 2 = – 0, 262 Che confrontata con x 1 app = 1, 726 e x 2 app = – 0, 387 Ci fornisce un errore relativo dell’ 8, 5% Tale errore può essere abbassato se si ingrandiscono le proporzioni dei segmenti.