Didattica speciale codici del linguaggio logico matematico scuola










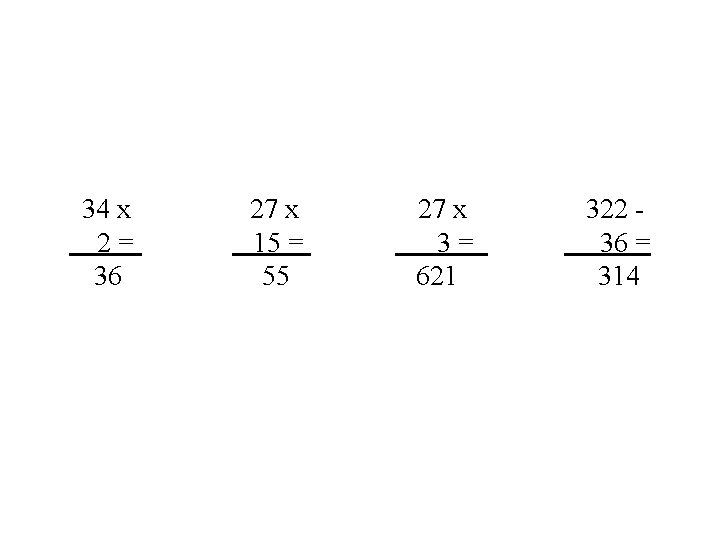


















































- Slides: 77

Didattica speciale: codici del linguaggio logico matematico scuola secondaria di secondo grado Paola Luisa Albano paolalisa. albano@gmail. com Corso di specializzazione per il sostegno agli alunni con disabilità a. a. 2016/2017

L’insegnante di sostegno è chiamato a gestire delle realtà molto diverse e complesse. Pertanto dovrà maturare la capacità di gestire situazioni diverse tra loro e che dipendono da: Allievo La sua storia Dalla classe di appartenenza Dall’insegnante

Le domande alle quali cercheremo di rispondere sono: Il processo di acquisizione degli strumenti aritmetici è supportato soltanto da capacità cognitive generali come il ragionamento, la memoria di lavoro e a lungo termine, il senso dello spazio oppure possediamo capacità numeriche innate? Come sono rappresentati i numeri nella nostra mente? Come facciamo a eseguire calcoli mentali più o meno complessi?

Possiamo affermare che esistono due tipi principali di espressione numerica: la parola – numero come ventitré e i numeri in formato arabico come 23. Qualunque sarà il formato utilizzato un numero può assumere significati diversi per: numerosità posizione seriale etichetta Inoltre emerge un’importante differenza tra i numeri e il linguaggio: la grandezza numerica è rappresentata in modo analogico e visuo – spaziale e non in modo simbolico - linguistico.

Le difficoltà di apprendimento in ambito matematico, possono riguardare l’ambito della lettura e scrittura dei numeri (processo lessicale) 135 145

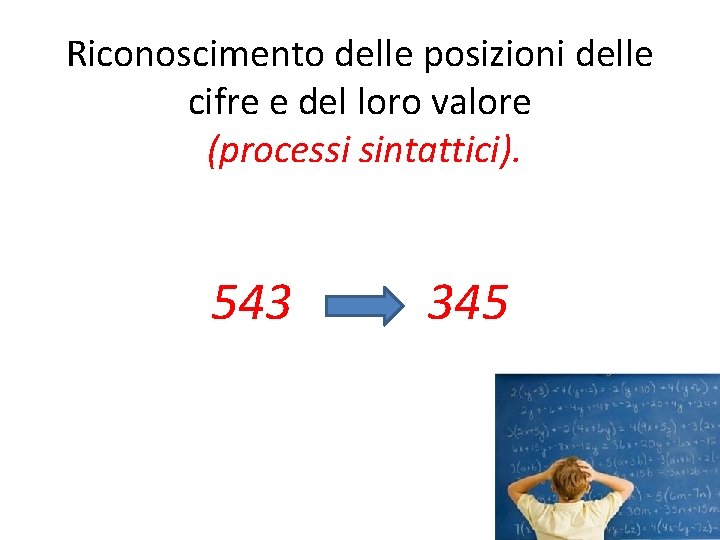
Riconoscimento delle posizioni delle cifre e del loro valore (processi sintattici). 543 345

Posizionamento sulla linea dei numeri, ordinamento di numerosità (processi semantici) 13 viene prima di 9

ERRORI NEL SISTEMA DI CALCOLO - Errori procedurali e di applicazione di strategie - Errori nel recupero di fatti aritmetici - Difficoltà visuo - spaziali

ERRORI PROCEDURALI Non utilizzo delle procedure di conteggio facilitanti Es. 2 + 8 partire a contare da 8 per aggiungere 2 Confusione tra semplici regole di accesso rapido Es. 5 x 0 = 5 e 5+0=5 Incapacità di tenere a mente i risultati parziali

ERRORI PROCEDURALI Difficoltà nella scelta delle prime cose da fare per affrontare una delle quattro operazioni (incolonnamento o meno, posizione dei numeri, …) Difficoltà nella condotta da seguire per la specifica operazione e nel suo mantenimento fino alla risoluzione Es. 75 – 6 = 71 dimenticata regola direzione Difficoltà nell’applicazione delle regole di prestito e riporto Es. 75 – 58 = 20 unità 5 – 8 = 0 decine 7 – 5 = 2 Difficoltà nel passaggio ad una nuova operazione perseverazione nel ragionamento precedente

ERRORI NEL RECUPERO DEI FATTI ARITMETICI. Effetto confusione tra il recupero di fatti aritmetici di addizione e quelli di moltiplicazione. Es: 3 x 3 = 6 Effetto inferenza: la semplice presentazione di due cifre può produrre un’attivazione automatica della somma. Es. 2 e 4 6

ERRORI VISUO SPAZIALI. Difficoltà nel riconoscimento dei segni di operazione Difficoltà nell’incolonnamento dei numeri
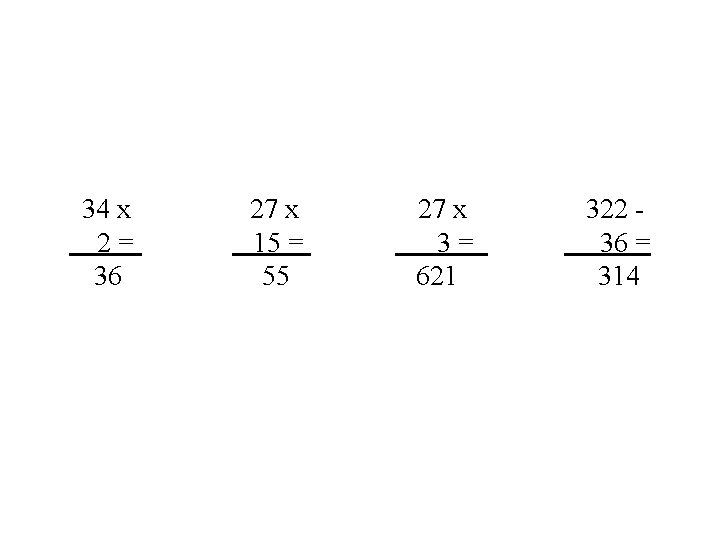
34 x 2= 36 27 x 15 = 55 27 x 3= 621 322 36 = 314

Modelli cognitivi dello sviluppo del numero del calcolo e dell’algebra. Il modello Piagetiano Case Fisher Gelman e Gallistel Butterworth Dehane

Il modello Piagetiano. Piaget suddivide lo sviluppo cognitivo in quattro stadi principali, ognuno caratterizzato da una modalità di pensiero qualitativamente diversa, resa possibile dall’emergere di un nuovo schema che si costruisce sulla base delle esperienze del bambino durante lo stadio precedente.

Stadi dello sviluppo cognitivo secondo Piaget Stadio Età Descrizione 0 -2 anni A 2 anni “comprende” il mondo in base a ciò che può fare con gli oggetti e con le informazioni sensoriali Preoperatorio 2 -6 anni Si rappresenta mentalmente gli oggetti e comincia a comprendere la loro classificazione in gruppi Operatorio concreto 6 -12 anni La capacità logica progredisce grazie allo sviluppo di nuove operazioni mentali (addizione, sottrazione, ecc. ) Operatorio formale Dai 12 anni È capace di organizzare le informazioni in modo sistematico e pensa in termini ipoteticodeduttivi Sensomotorio 16

Fra gli innumerevoli studi, Piaget approfondì la formazione del simbolo numerico nei bambini. I fattori che contribuiscono alla costruzione del numero sono molteplici. In particolare ne ricordiamo due: La conservazione della quantità La corrispondenza biunivoca

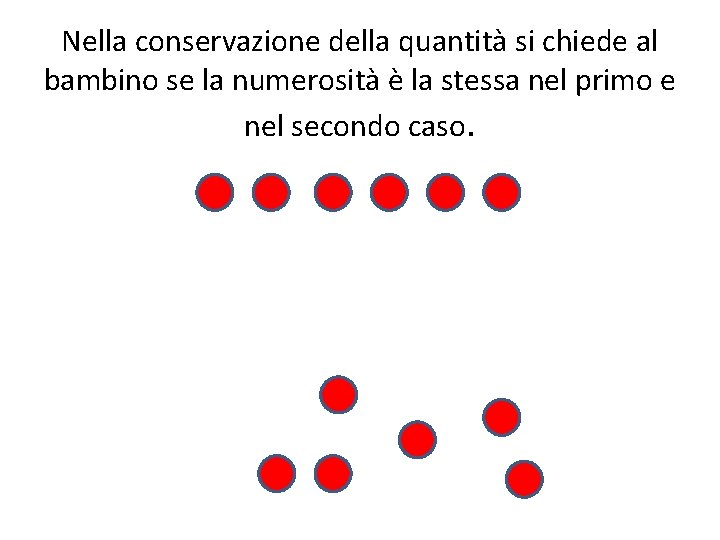
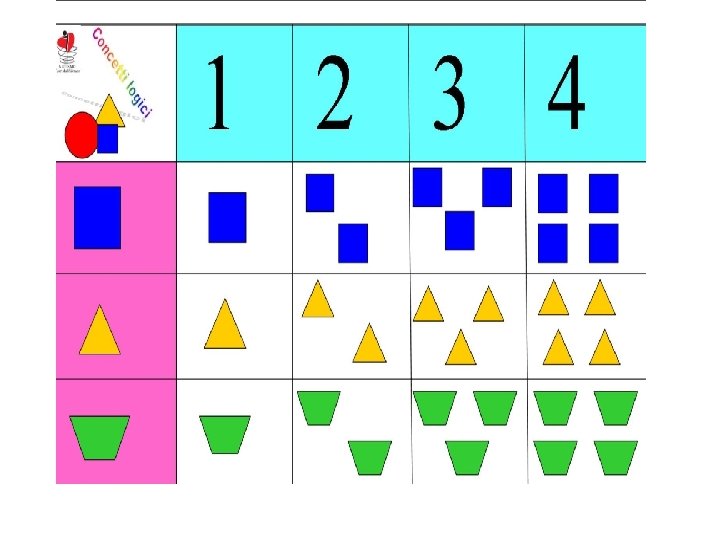
Nella conservazione della quantità si chiede al bambino se la numerosità è la stessa nel primo e nel secondo caso.

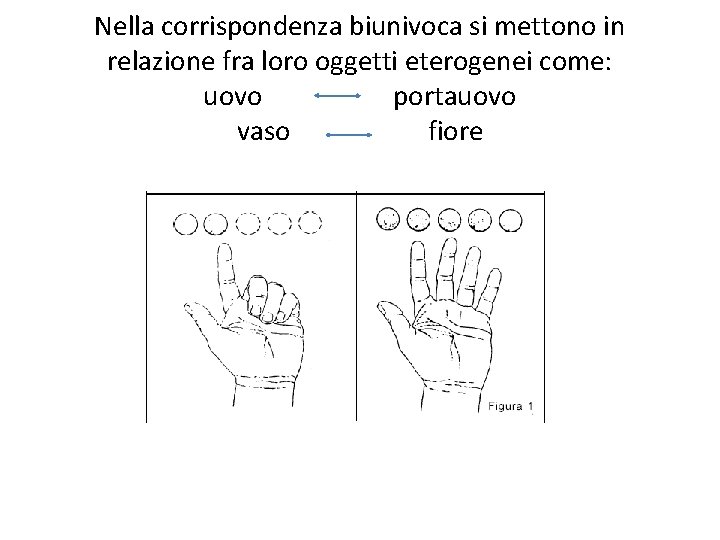
Nella corrispondenza biunivoca si mettono in relazione fra loro oggetti eterogenei come: uovo portauovo vaso fiore

Molti dei problemi e dei limiti delle teorie di Piaget vengono sollevati da un gruppo di psicologi evolutivi denominati «neopiagetiani» . Essi sono piagetiani perché credono negli stadi, nelle sequenze e nel cambiamento strutturale, ma contestano l’assenza, nella teoria di Piaget, di costrutti quali abilità, capacità limitata di memoria e risorse attentive.

Il neopiagetiano Case (1985) aveva considerato che la capacità di memoria aumenterebbe con il miglioramento dei processi mentali in genere, proponendo che il senso del numero dipenda da potenti schemi organizzatori, detti strutture concettuali centrali. Nello sviluppo del numero si ipotizza che dapprima si consolidino gli schemi verbali (digitale) e spaziale (analogico). Poi dalla loro interconnessione si produca una linea mentale del conteggio, infine si sviluppano le rappresentazioni di proprietà numeriche.

Lo sviluppo del numero si articola in 3 momenti: 1. Consolidamento di due schemi primitivi uno verbale, digitale e sequenziale (prime operazioni di conteggio verbale) l’altro spaziale e analogico che consente di individuare situazioni di numerosità relativa (di più/di meno) e di operatività concreta (aggiungere/togliere).

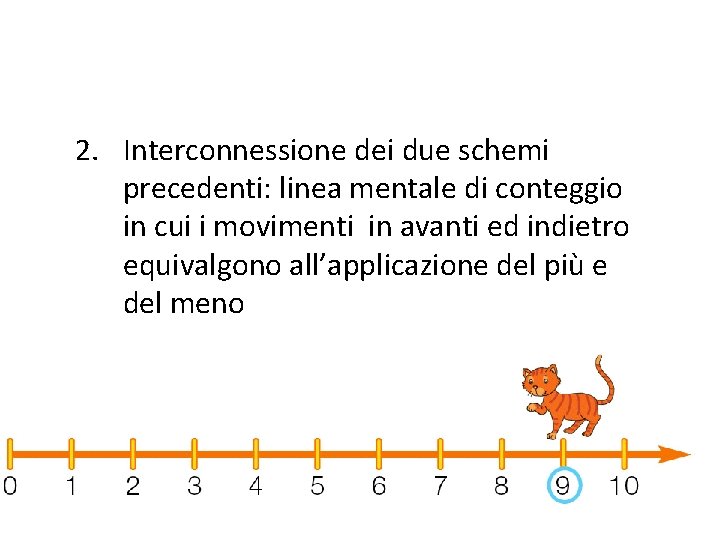
2. Interconnessione dei due schemi precedenti: linea mentale di conteggio in cui i movimenti in avanti ed indietro equivalgono all’applicazione del più e del meno

3. Differenziazione di nuovi elementi, possibile solo attraverso la rappresentazione delle proprietà numeriche. Il bambino differenzia così unità, decine, centinaia e a distinguere il numero oggetto dal numero operatore.

All’interno della sua “teoria delle abilità” Fischer (1980) enfatizza invece il ruolo delle esperienze specifiche dell’ambiente, che, stimolando abilità non applicabili a tutti i domini, potrebbero spiegare le differenze a livello cognitivo nei diversi domini. Propone infatti l’idea di uno sviluppo in buona parte dominio – specifico, ossia ristretto ad un particolare tipo di conoscenza.

In una recente ricerca si è indagato per capire se alcuni concetti geometrici sono intrinseci al pensiero umano, ovvero se si riescono a individuare dei principi geometrici innati. Per rispondere a questa domanda hanno testato bambini e adulti di una tribù amazzonica, chiamata Mundurukù. I bambini e gli adulti hanno sempre vissuto nel villaggio isolato e non avevano ricevuto nessun tipo di educazione formale. C’è da dire che il linguaggio numerico dei Mundurukù è molto povero e possiedono le parole – numero fino a cinque. Per quanto riguarda la geometria possiedono parole specifiche come linea, punto, lato e figura curva.

I risultati dimostrano l’esistenza di principi geometrici innati, ovvero gli indigeni sono in grado di rispondere ad item appartenenti alle seguenti categorie di concetti geometrici come ad esempio linea, punto, perpendicolarità, angolo retto al concetto di quadrato, triangolo e cerchio. Tuttavia gli indigeni non sono in grado di rispondere a domande relative a traslazioni o rotazioni di figure geometriche. I bambini americani scolarizzati, mostravano esattamente le stesse prestazioni dei bambini indigeni dell’Amazzonia della stessa età. Tale dato dimostra che le enormi differenze culturali ed educative non vanno a incidere su quelli che possono essere definiti i concetti geometrici a base innata che sono presenti indipendentemente dalla cultura e dall’educazione.

Butterwort è un sostenitore della tesi innatista del cervello matematico. Se i bambini nascono con la capacità innata di contare, perché impiegano circa sei anni per potersene servire in modo pieno?

Le difficoltà che devono affrontare sono: Conoscere i vocaboli Collegare ciascuna parola ad un solo oggetto Capire la cardinalità di un insieme • Per esempio per contare fino a cinque necessita di cinque parole e ripeterle sempre nello stesso senso • Nessuna parola deve essere utilizzata più volte e tutti gli oggetti devono essere contati. Bisogna cioè creare una corrispondenza biunivoca fra le parole e gli oggetti • L’ultimo numero va ripetuto perché rappresenta il numero degli oggetti contati cioè la cardinalità.

Per tutti la struttura innata del contare arriva massimo fino a dieci e, pertanto, dobbiamo imparare il sistema dei simboli numerici, basato sulla notazione posizionale.

In questo ambito i bambini di lingua cinese godono di uno straordinario vantaggio rispetto ai bimbi europei. Infatti, i cinesi, superata la difficoltà dei primi dieci numeri ( tra l’altro monosillabici con ulteriore vantaggio per la memorizzazione) l’undici diventa dieci- uno poi dieci – due ecc.

In recenti studi relativi al funzionamento delle aree celebrali attraverso neuro – immagini, fornite dalla Pet e dalla risonanza magnetica, è stato possibile osservare le aree coinvolte in vari tipi di processo: compiti visuo spaziale, linguaggio, attenzione, calcolo, ecc.

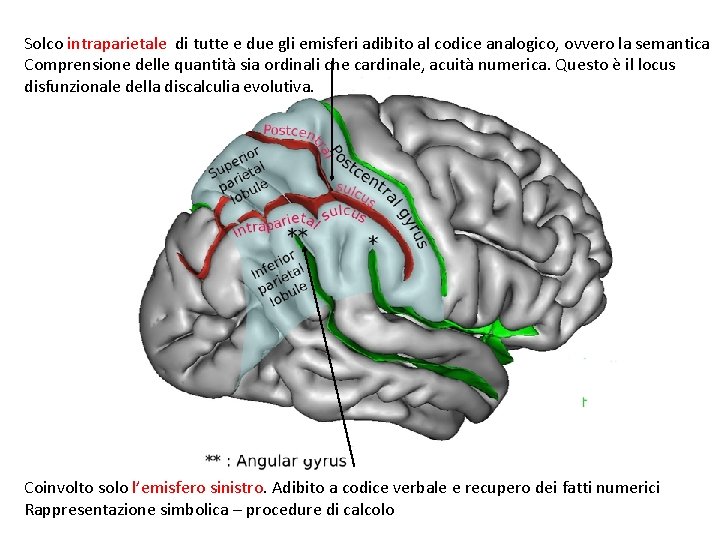
Solco intraparietale di tutte e due gli emisferi adibito al codice analogico, ovvero la semantica Comprensione delle quantità sia ordinali che cardinale, acuità numerica. Questo è il locus disfunzionale della discalculia evolutiva. Coinvolto solo l’emisfero sinistro. Adibito a codice verbale e recupero dei fatti numerici Rappresentazione simbolica – procedure di calcolo

Aree occipito – temporali inferiori ventrali per il codice visivo arabico

Le aree sono tutte strettamente connesse con l’amigdala, da cui scaturisce il piacere della percezione del sé competente, associata al successo in ambito matematico, o al contrario, che porta al rifiuto del confronto per preservare l’Io.

Gelman & Gallistel Secondo questi ricercatori nello studio dello sviluppo del concetto di numero è necessario distinguere due tipi di processo Il processo di astrazione Il processo di ragionamento Rappresentazione di numerosità subitizzazione Capacità di fare inferenze (maggiore, minore) e trasformazioni numeriche (Addizione, sottrazione)

Queste due abilità sono strettamente connesse, infatti, l’uso del ragionamento numerico dipende dall’avere maturato la rappresentazione mentale dei valori numerici. Gelman e Gallistel contestavano a Piaget di ritenere che il contare fosse un automatismo senza alcuna relazione con le operazioni numeriche.

Si ipotizza che il bambino possieda una comprensione di principi che regolano il contare. I cinque principi che governano e definiscono il processo del contare possono essere così sintetizzati.

Il principio di iniettività il principio dell’ordine stabile il principio di cardinalità il principio di astrazione il principio dell’irrilevanza dell’ordine

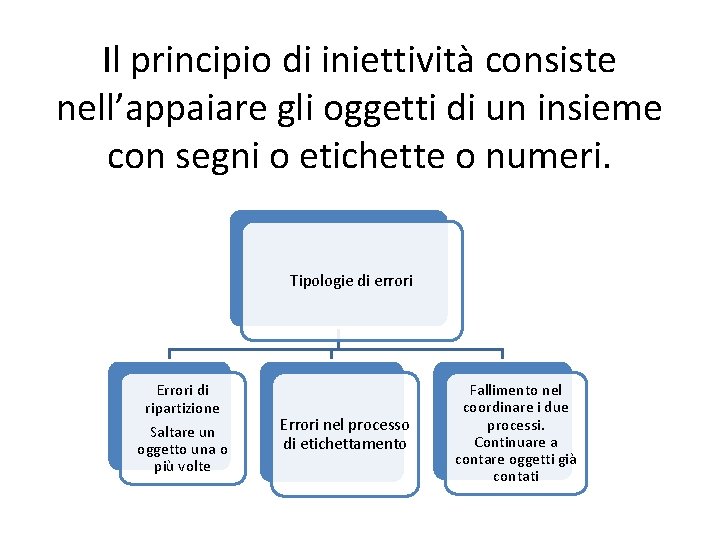
Il principio di iniettività consiste nell’appaiare gli oggetti di un insieme con segni o etichette o numeri. Tipologie di errori Errori di ripartizione Saltare un oggetto una o più volte Errori nel processo di etichettamento Fallimento nel coordinare i due processi. Continuare a contare oggetti già contati

Nel principio dell’ordine stabile le etichette usate per etichettare gli oggetti devono essere ordinate e scelte in ordine stabile. Se il bambino conosce i numeri da uno a cinque questi devono essere tenuti sempre nello stesso ordine.

Il principio di cardinalità afferma che l’etichetta finale ha un significato speciale. Infatti, questa etichetta, a differenza delle altre, rappresenta la cardinalità dell’insieme. Il bambino deve essere in grado di indicare il numero di cioccolatini con l’ultima parola numero che ha usato: “ 1, 2, 3, 4. Quattro cioccolatini”

Il principio di astrazione riguarda il come contare. I bambini riescono a contare oggetti eterogenei e anche lo spazio fra essi e questo rappresenta il massimo dell’astrazione mentale.

Il principio dell’irrilevanza dell’ordine prevede che in qualsiasi modo si conti la cardinalità è sempre la stessa

Dehaene sostiene, in accordo con Butterworth, che siamo dotati sin dalla nascita di una rappresentazione mentale della quantità molto simile a quella di molti animali.

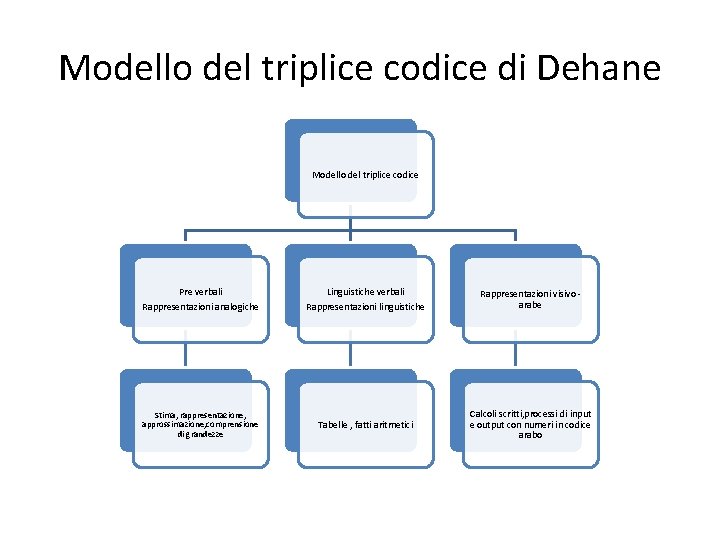
Modello del triplice codice di Dehane Modello del triplice codice Pre verbali Linguistiche verbali Rappresentazioni analogiche Rappresentazioni linguistiche Stima, rappresentazione, approssimazione, comprensione di grandezze Tabelle , fatti aritmetici Rappresentazioni visivo - arabe Calcoli scritti, processi di input e output con numeri in codice arabo

Un particolare richiamo va fatto, in questo quadro sullo sviluppo tipico delle abilità numeriche, al rapporto fra queste e la gnosia digitale come la “Sindrome di Gerstman”. Agnosia digitale Disorientamento destra sinistra È causata in genere da lesione del lobo parietale sinistro, in particolare della circonvoluzione angolare. Acalculia Agrafia

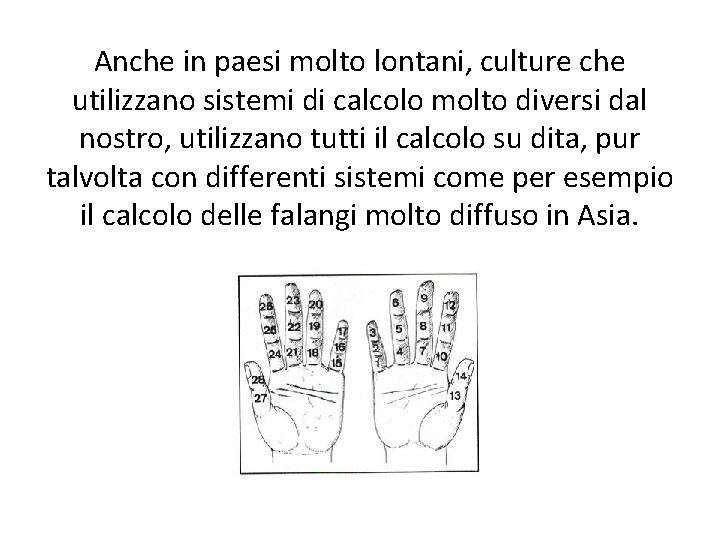
Le dita, svolgono il compito di rappresentare visivamente le quantità numeriche e di tener traccia del conteggio verbale. Questa è una conferma del fatto che le dita supportano, facilitano e in un certo senso guidano i processi di base della cognizione numerica. A sostegno di questa tesi si può porre l’attenzione sull’uso del conteggio digitale nelle varie culture.

Anche in paesi molto lontani, culture che utilizzano sistemi di calcolo molto diversi dal nostro, utilizzano tutti il calcolo su dita, pur talvolta con differenti sistemi come per esempio il calcolo delle falangi molto diffuso in Asia.

Ulteriori studi sulla plasticità neurale hanno inoltre confermato come lo sviluppo dei circuiti celebrali sia sì legato alla programmazione genetica, ma si realizzi anche attraverso esperienze post natali, nonché anche attraverso esperienze specifiche di apprendimento e potenziamento: il numero di ramificazioni dendritiche e le sinapsi si moltiplica e modifica nel tempo fino a formare delle vere e proprie rete neuronali che “scolpiscono” il cervello.

Tale cognizione partirebbe da meccanismi innati, che abbiamo dunque in dotazione genetica, quali il subitizing o immediatizzazione e il riconoscimento di n+1 e n-1, e procederebbe poi per la conquista di capacità di quantificazione analogica preverbale, per confluire, infine, in quella verbale.

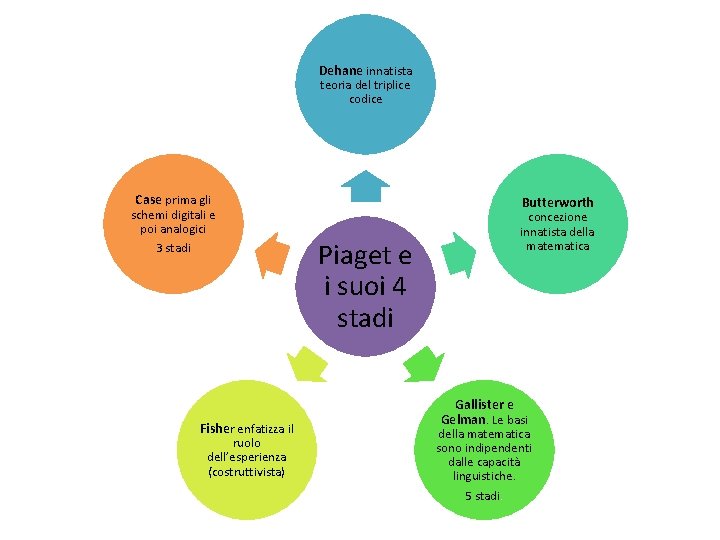
Dehane innatista teoria del triplice codice Case prima gli schemi digitali e poi analogici 3 stadi Fisher enfatizza il ruolo dell’esperienza (costruttivista) Butterworth Piaget e i suoi 4 stadi concezione innatista della matematica Gallister e Gelman. Le basi della matematica sono indipendenti dalle capacità linguistiche. 5 stadi.

Studio di caso. Un ragazzo di 15 anni ha una diagnosi di ritardo mentale grave in comorbilità con disturbo di attenzione e iperattività e compromissione della memoria di lavoro. Ha qualche difficoltà motoria, soprattutto nella coordinazione e nell’equilibrio. Buone le abilità visuo - percettive.

Le capacità di lettura e di linguaggio sono pari a quelle di un bambino di seconda primaria, mentre quelle di scrittura sono assimilabili ad una prima di classe primaria con tratto grafico rigido e poco controllato.

Si tratta di un bambino adottato in cui hanno iniziato ad emergere i primi sintomi intorno ai due anni e, in seguito a ciò, i genitori hanno dovuto affrontare un periodo di forte tensione sfociato in una loro separazione. Dunque ad un substrato organico, già comunque compromesso, si è aggiunta una ferita sul piano relazionale - affettiva

Nell’ambito delle prestazioni matematiche si caratterizza per una forte componente ansiosa, una grande impulsività e casualità nelle risposte, un’eterocronia di sviluppo, rispetto alle altre aree, a netto svantaggio di quella logico matematica. In uscita dalla scuola primaria era stato definito in grado di contare in senso progressivo fino a 20 e di associare numero e quantità fino a 10.

Nella classe della scuola secondaria di secondo grado è stata intrapresa un’attività per lo sviluppo delle abilità di addizione e sottrazione in N. Al termine dell’anno scolastico viene riferito che l’alunno è in grado di eseguire semplici addizioni in riga senza riporto e verificarne il risultato con la calcolatrice. Nel secondo anno, assunte le difficoltà logiche e di astrazione, sono stati scelti come obiettivo la conoscenza delle quattro operazioni e la loro esecuzione con la calcolatrice. L’alunno legge i numeri fino a 10, con qualche incertezza fra il 6 il 9 e il 10. Legge come quattordici indifferentemente il 14 e il 41. Quindi ci sono problemi di sintassi del numero. Non è in grado di compiere la numerazione inversa.

Da un confronto con gli studi di Piaget è possibile individuare alcuni step evolutivi non raggiunti (competenze di seriazione e processi di reversibilità). Facendo riferimento agli studi di Case vediamo che il ragazzo ha problemi con l’utilizzo della memoria di lavoro. Rileviamo anche come siano intaccate alcune aree domino – specifiche e questo spiegherebbe l’eterocronia nel campo logico matematico. Il ragazzo presenta difficoltà di riconoscimento e confronto di numerosità che dovrebbero essere innate. Quindi vi è stato un gap nel concetto di irrilevanza dell’ordine e astrazione del numero previsti da Gelman e Gallistel. Bisogna quindi attuare un intervento in cui la strutturazione e la consapevolezza della mediazione si basino sulle più recenti e comprovate teorie dello sviluppo del senso del numero, andando ad agire realmente nella zona di sviluppo prossimale del soggetto, nel dominio di specificità delle competenze oggetto dell’intervento.

Ipotesi di intervento. Si è cominciato a lavorare sul riconoscimento e confronto di numerosità, di grandezze, per arrivare ad abilità di seriazione e di enumerazione inversa, limitando , per ora, il campo di azione alla decina.

Per indagare sulle abilità legate all’intelligenza numerica del ragazzo si è utilizzata la batteria BIN 4 -6 (Molin, Poli, Lucangeli). La batteria presenta prove per i processi semantici, di conteggio, lessicali e di seriazione. Si è adoperata tale batteria perché in presenza di problemi gravi di presintassi numerica.


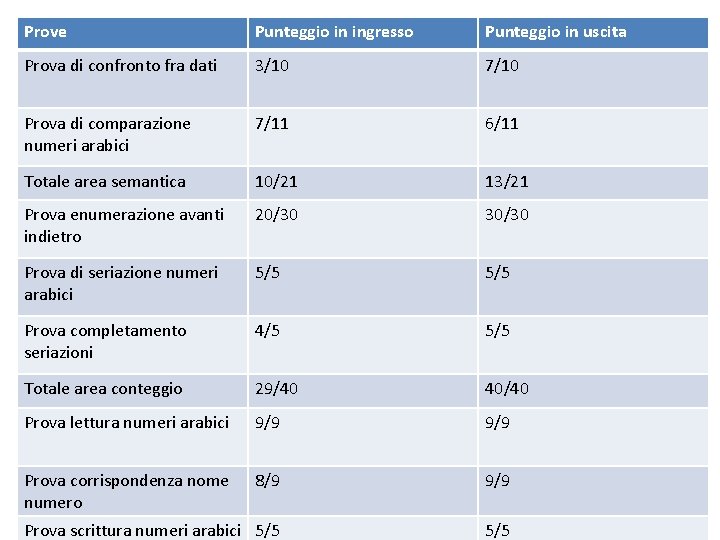
Prove Punteggio in ingresso Prova di confronto fra dati 3/10 Prova di comparazione numeri arabici 7/11 Totale area semantica 10/21 Prova enumerazione avanti indietro 20/30 Prova di seriazione numeri arabici 5/5 Prova completamento seriazioni 4/5 Totale area conteggio 29/40 Prova lettura numeri arabici 9/9 Prova corrispondenza nome numero 8/9 Prova scrittura numeri arabici 5/5

Subito si incontrano le prime difficoltà, perché il ragazzo non è abituato al confronto. Si lavora dunque per creare l’abitudine e il confronto fra oggetti, situazioni, immagini, dimensioni e quantità.




Nel contempo cominciamo a lavorare sulla reversibilità: sulle scale sono stati attaccati dei cartelli con i numeri in successione. Iniziamo a salire e scendere le scale leggendo i numeri. Ci si sofferma a guardare il numero che viene prima e quello che viene dopo. Cosa succede se andiamo due gradini avanti piuttosto che tre in dietro?


In aula prosegue il lavoro con il software della Clementoni: Cdvertiamo http: //www. ddrivoli 1. it/PORTOMATE/giochi_di_matematica. htm#matepiccoli http: //www. istitutopalatucci. it/free. html http: //pianetabambini. it/app-imparare-contare-numeri-bambini/ http: //www. maestrantonella. it/traduzione%20 software%20 Gen. Magic. html

In sintesi le azioni dell’intervento possono essere così schematizzate.

Lavorare per Immagini Supportarsi tramite azioni fisiche Utilizzare software ludico Utilizzare scala dei numeri reale e grafica Giochi mirati a sviluppare la quantificazione preverbale e il subitizing (domino, carte semplificate) Conteggio sulle dita Una forte mediazione affinché l’alunno provi sensazione di piacere, come ascoltare la musica e il riconoscimento dei compagni

Dopo due mesi di trattamento il ragazzo ha imparato la numerazione inversa, è sicuro nei processi di seriazione e nel confronto di quantità. Sono , inoltre, diminuite le risposte impulsive. Appaiono però, ancora carenti i riconoscimenti di quantità. Si procede, ancora per un mese sul riconoscimento analogico di quantità in modo ludico facendogli trascrivere i numeri e facendo confronti con le carte e il domino.

Prove Punteggio in ingresso Punteggio in uscita Prova di confronto fra dati 3/10 7/10 Prova di comparazione numeri arabici 7/11 6/11 Totale area semantica 10/21 13/21 Prova enumerazione avanti indietro 20/30 30/30 Prova di seriazione numeri arabici 5/5 Prova completamento seriazioni 4/5 5/5 Totale area conteggio 29/40 40/40 Prova lettura numeri arabici 9/9 Prova corrispondenza nome numero 8/9 9/9 Prova scrittura numeri arabici 5/5

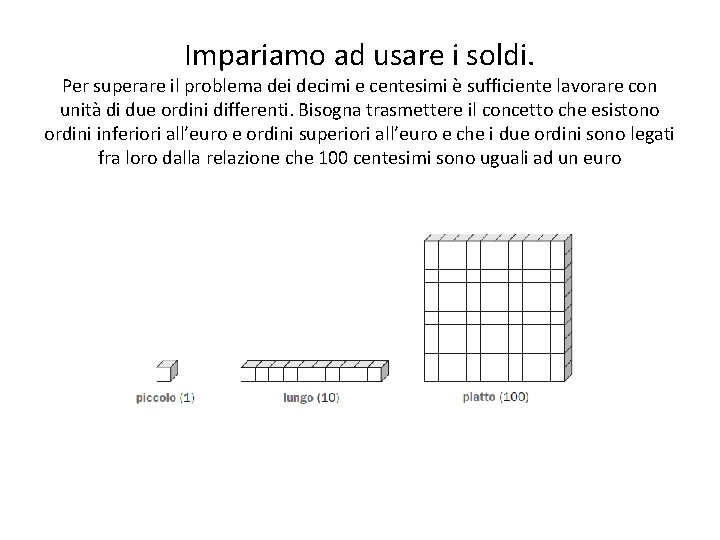
Impariamo ad usare i soldi. Per superare il problema dei decimi e centesimi è sufficiente lavorare con unità di due ordini differenti. Bisogna trasmettere il concetto che esistono ordini inferiori all’euro e ordini superiori all’euro e che i due ordini sono legati fra loro dalla relazione che 100 centesimi sono uguali ad un euro



 Didattica speciale per ambito logico matematica primaria
Didattica speciale per ambito logico matematica primaria Codici del linguaggio logico matematico
Codici del linguaggio logico matematico Termini della moltiplicazione
Termini della moltiplicazione Codici del linguaggio logico e matematico
Codici del linguaggio logico e matematico Didattica speciale per ambito logico matematica primaria
Didattica speciale per ambito logico matematica primaria Pensiero progettuale freddo
Pensiero progettuale freddo Didattica speciale cos'è
Didattica speciale cos'è Correspondencia biunivoca
Correspondencia biunivoca Sentido lógico-matemático convencional dos conectivos
Sentido lógico-matemático convencional dos conectivos Giuseppe peano carola crosio
Giuseppe peano carola crosio Favola del lupo e dell'agnello
Favola del lupo e dell'agnello Strategie personalizzate
Strategie personalizzate Ossido di piombo usato per decorare antichi codici
Ossido di piombo usato per decorare antichi codici Studiare unife my desk
Studiare unife my desk Codici ridondanti
Codici ridondanti Programmazione cnc simulator
Programmazione cnc simulator Codici miniati divina commedia
Codici miniati divina commedia Frasi hp rifiuti
Frasi hp rifiuti Delibera 274 tim
Delibera 274 tim Negano i postulati del matematico degli elementi
Negano i postulati del matematico degli elementi Siugp
Siugp A zacinto campi semantici
A zacinto campi semantici Strumenti di elaborazione del linguaggio naturale
Strumenti di elaborazione del linguaggio naturale Livelli del linguaggio
Livelli del linguaggio Is vandaag een speciale dag
Is vandaag een speciale dag Metodeafsnit universitet
Metodeafsnit universitet Teorema del resto
Teorema del resto Coloratia pas
Coloratia pas Scomposizione in fattori primi polinomi
Scomposizione in fattori primi polinomi Quest'anno per natale vorrei un albero speciale
Quest'anno per natale vorrei un albero speciale Speciale dank aan
Speciale dank aan Poesia rima alternata
Poesia rima alternata Persona unica significato
Persona unica significato Trinomio speciale
Trinomio speciale Note de synthèse exemple
Note de synthèse exemple Ejemplo de marco lógico de un proyecto productivo
Ejemplo de marco lógico de un proyecto productivo Que es la parte intangible del computador
Que es la parte intangible del computador Evento certo
Evento certo Approccio matematico della comunicazione
Approccio matematico della comunicazione Matematico famoso
Matematico famoso Franciscus vieta
Franciscus vieta Segundo o matemático leopold kronecker
Segundo o matemático leopold kronecker Monge matematico
Monge matematico Figure simmetriche da disegnare
Figure simmetriche da disegnare Napier matematico
Napier matematico Definizione di insieme matematico
Definizione di insieme matematico De giorgi matematico
De giorgi matematico Modelado matematico de sistemas fisicos
Modelado matematico de sistemas fisicos Biografia de diofanto wikipedia
Biografia de diofanto wikipedia Modelo matemático
Modelo matemático Caja mackinder
Caja mackinder Movimientos microsacádicos
Movimientos microsacádicos Georg simon ohm
Georg simon ohm El matematico griego pitagoras nacio en el año 580
El matematico griego pitagoras nacio en el año 580 Modelado matematico de sistemas fisicos
Modelado matematico de sistemas fisicos Modelado matematico de sistemas fisicos
Modelado matematico de sistemas fisicos Modelado matematico de sistemas fisicos
Modelado matematico de sistemas fisicos Sistemas
Sistemas Modelo matematico
Modelo matematico Matematico e fisico greco
Matematico e fisico greco Attributo
Attributo Sfc alternative
Sfc alternative Istruzioni iterative
Istruzioni iterative Ladder simbologia
Ladder simbologia Linguaggio di programmazione imperativo
Linguaggio di programmazione imperativo Ladder i
Ladder i Linguaggio kop
Linguaggio kop 4 assioma della comunicazione
4 assioma della comunicazione Divisione in sillabe alla sera
Divisione in sillabe alla sera Struttura del testo drammatico
Struttura del testo drammatico Linguaggio paraverbale
Linguaggio paraverbale Linguaggio ad alto livello informatica
Linguaggio ad alto livello informatica Linguaggio brunelleschiano
Linguaggio brunelleschiano Linguaggio sql esempi
Linguaggio sql esempi Rappresentazione algoritmo informatica
Rappresentazione algoritmo informatica Programmazione awl
Programmazione awl Dowhile c
Dowhile c Osu! linguaggio di programmazione
Osu! linguaggio di programmazione