sus dgitos tienen una correspondencia exacta con los

• sus dígitos tienen una correspondencia exacta con los valores de una variable lógica 1 - Una magnitud numérica expresada en código binario requiere más de tres veces tantos dígitos como el número equivalente 2 - Las conversines de binario a decimal y inversa y directa son relativamente complicadas, cada digito binario puede afectar a cada decimal y viceversa Para subsanar la primer desventaja se pueden utilizar los códigos octal o hexadecimal. Para la segunda, se puede utilizar el sistema de representación decimal codificado binario (BCD) o el código denomindo reflejado

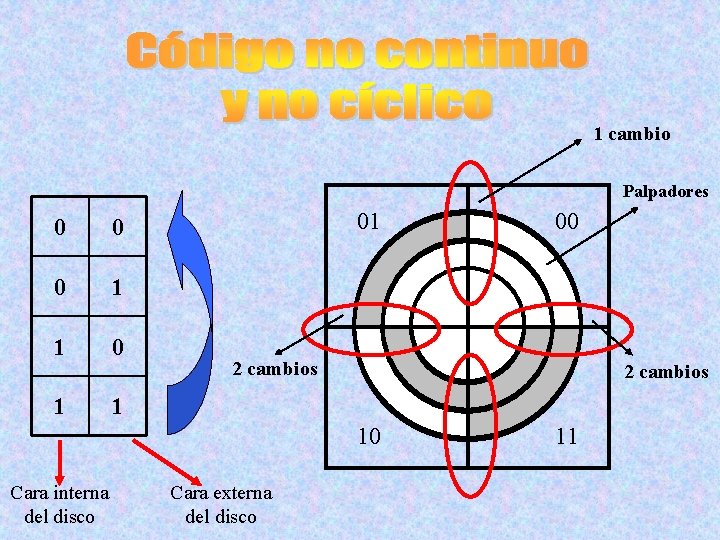
1 cambio Palpadores 0 0 0 1 1 01 2 cambios 1 10 Cara interna del disco 00 Cara externa del disco 11

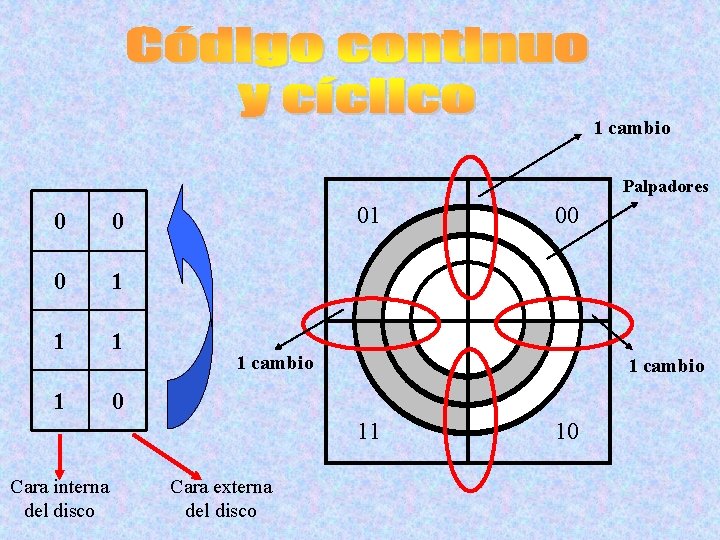
1 cambio Palpadores 0 0 0 1 1 01 1 cambio 0 11 Cara interna del disco 00 Cara externa del disco 10

conjunto de significado o reglas asociadas a un grupo de bits. Toda combinación de datos posee un significado determinado, basado en reglas determinadas ES UN CÓDIGO porque al pasar de una combinación válida del código a la siguiente, se cambia un único bit CONTINÚO Y CÍCLICO porque también hay un bit de diferencia entre la última y la primera combinación válida

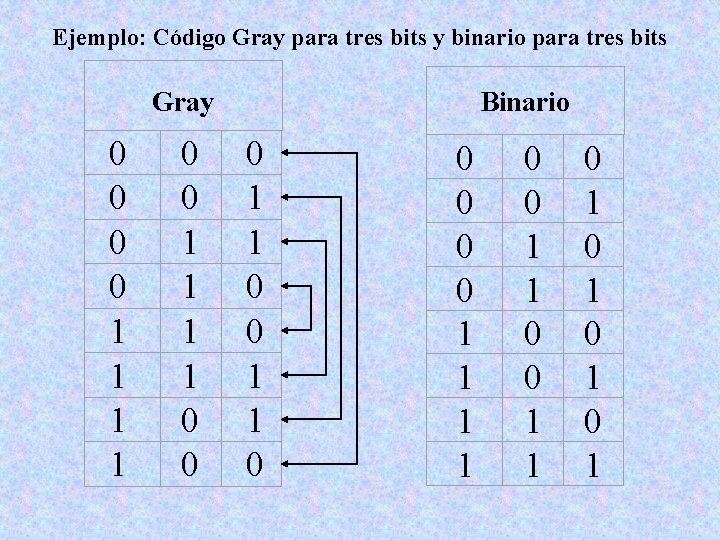
Ejemplo: Código Gray para tres bits y binario para tres bits Gray 0 0 1 1 1 1 0 0 Binario 0 1 1 0 0 1 1 0 1 0 1

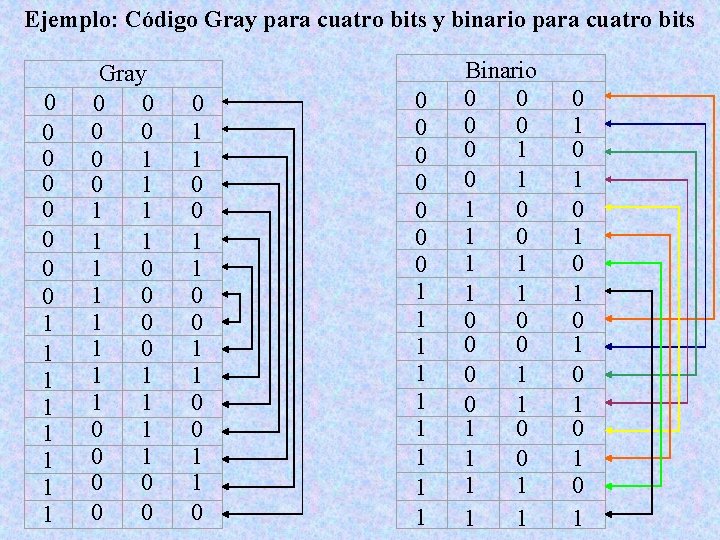
Ejemplo: Código Gray para cuatro bits y binario para cuatro bits 0 0 0 0 1 1 1 1 Gray 0 0 0 1 1 1 1 0 1 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 Binario 0 0 0 0 0 1 0 1 1 1 1 0 1 0 1

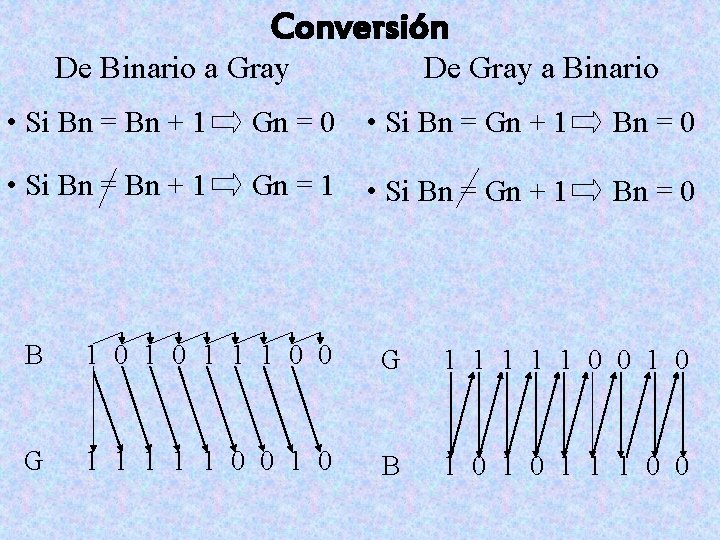
Conversión De Gray a Binario De Binario a Gray • Si Bn = Bn + 1 Gn = 0 • Si Bn = Gn + 1 Bn = 0 • Si Bn = Bn + 1 Gn = 1 • Si Bn = Gn + 1 Bn = 0 B 1 0 1 1 1 0 0 G 1 1 1 1 1 0 0 1 0 B 1 0 1 1 1 0 0

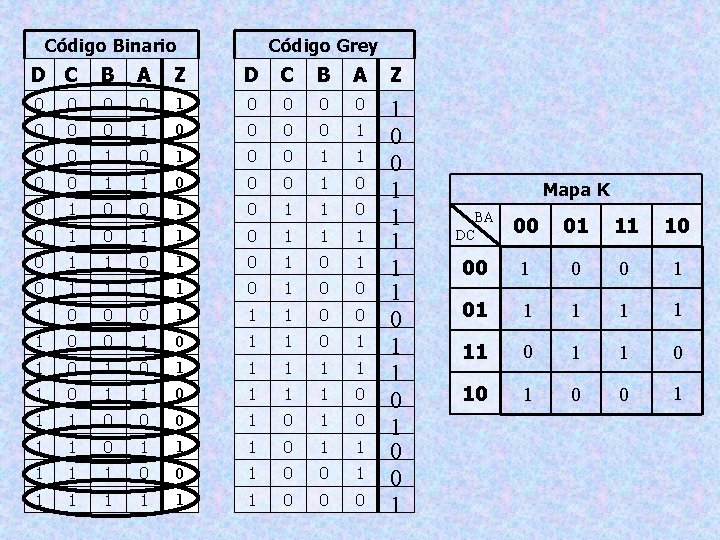
Código Binario Código Grey D C B A Z 0 0 0 0 1 0 0 1 1 0 0 0 1 0 1 1 1 0 1 0 1 0 1 0 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 1 1 0 0 1 1 1 1 0 0 0 1 1 1 0 0 1 Mapa K BA DC 00 01 11 10 00 1 01 1 1 11 0 10 1 0 0 1

ANALISIS dado un circuito encontrar la función lógica que cumple a su salida SINTAXIS encontrar el circuito suponiendo que se parte de una especificación 1. Tabular la especificación (hacer tabla de verdad) 2. Mapearla (hacer el mapa de Veitch-Karnaugh) 3. Simplificarla (hacer la expresión más simple) 4. Implementarla (colocar las compuertas para realizar esa función)

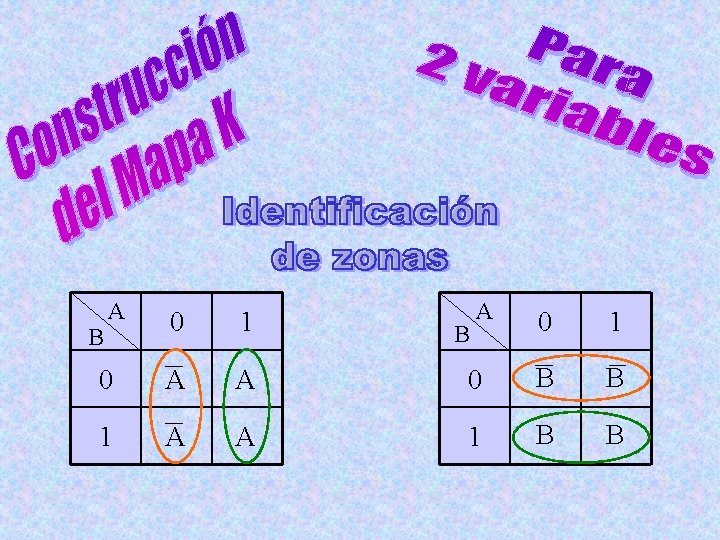
Mapa de Veitch-Karnaugh: Construcción con 2 variables B A Z 0 0 1 1 1 0 Mapa K A 0 1 0 0 1 1 1 0 B

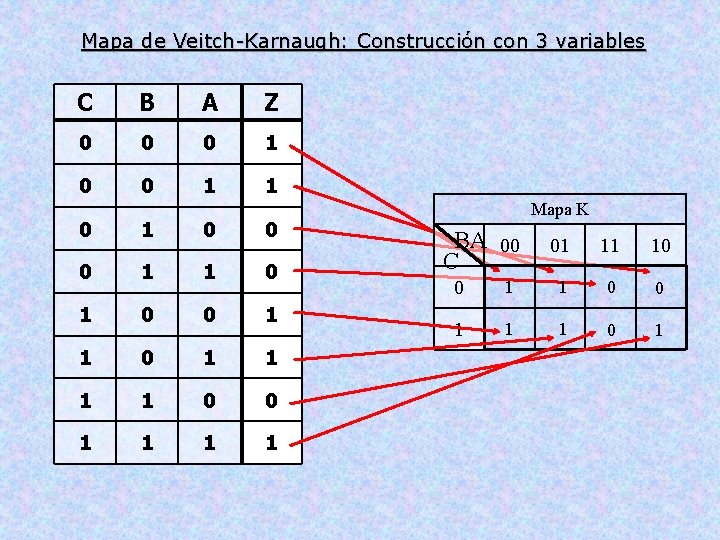
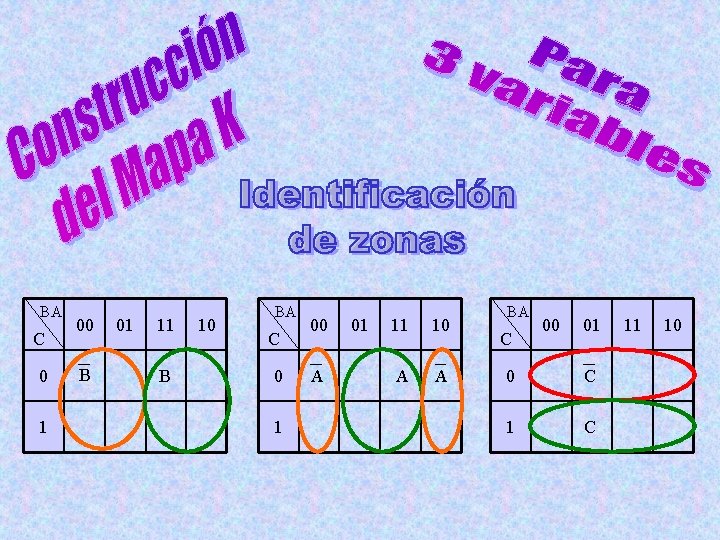
Mapa de Veitch-Karnaugh: Construcción con 3 variables C B A Z 0 0 0 1 1 0 1 1 1 1 0 0 1 1 Mapa K BA 00 C 01 11 10 0 1 1 1 0 1

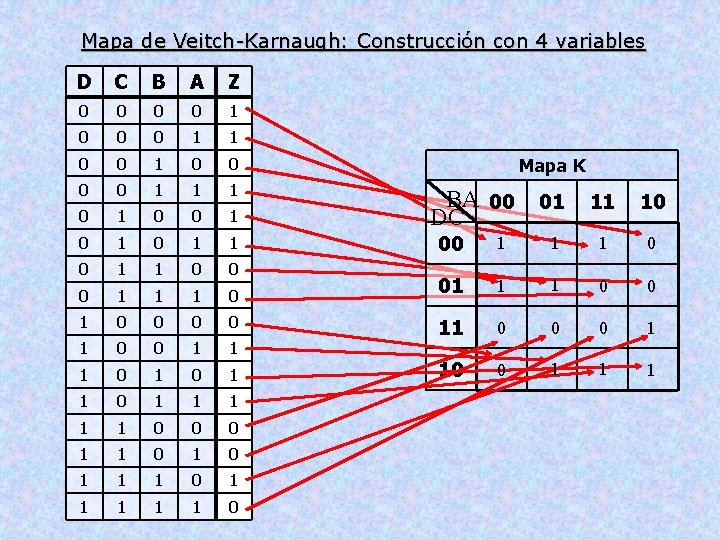
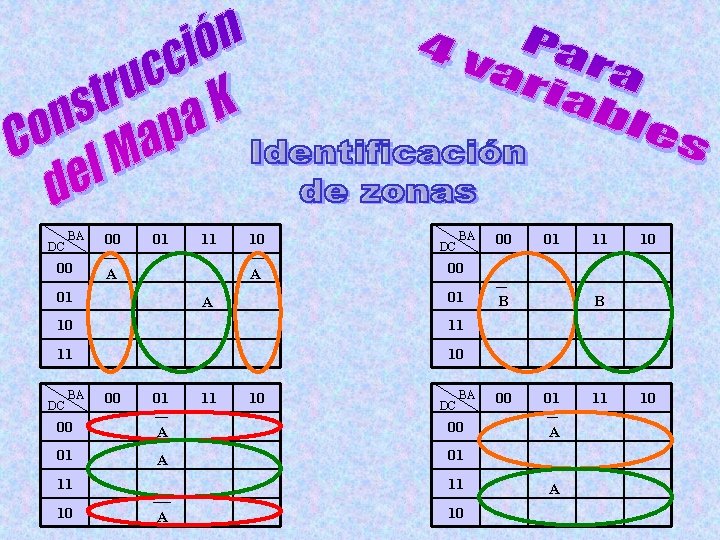
Mapa de Veitch-Karnaugh: Construcción con 4 variables D C B A Z 0 0 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 Mapa K BA 00 DC 01 11 10 00 1 1 1 0 0 0 0 0 1 0 1 1 11 0 1 10 0 1 1 1 1 1 0 0 0 1 1 1 0 1 1 1 0

1. Se lo utiliza para sintetizar funciones lógicas en forma gráfica y rápida. 2. Muy cómodo para sintetizar problemas de más de dos variables de entrada. 3. Permite sintetizar funciones sin aplicar las leyes del álgebra de Boole. 4. Agrupando los “ 1” obtenemos expresiones con la suma de productos; mientras que si se agrupan los “ 0” se obtienen productos de la suma. 5. Para realizar el mapa K se utiliza el código Gray. 6. Se recorre de la siguiente manera: BA DC 00 01 11 10 00 00 1 comienzo 2 4 3 01 01 5 6 8 7 11 10 11 13 14 16 15 10 9 10 00 01 11 10 final 12 11

A 0 1 0 A A 1 A A B A 0 1 0 B B 1 B B B

BA C 0 1 00 B 01 11 B 10 BA C 0 1 00 A 01 11 10 A A BA C 00 01 0 C 11 10

DC BA 00 00 01 11 A 10 A 01 DC BA 10 11 11 10 DC BA 00 01 A 01 11 10 11 A 01 11 10 00 01 A 00 10 B B 00 01 A A 11 10

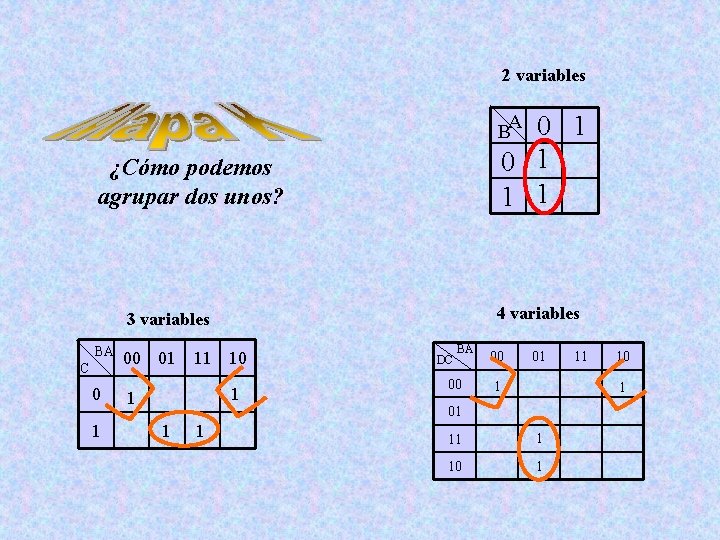
2 variables 0 1 1 1 BA ¿Cómo podemos agrupar dos unos? 4 variables 3 variables BA C 0 1 00 01 11 10 1 1 DC BA 00 00 01 1 11 10 1 01 11 1 10 1

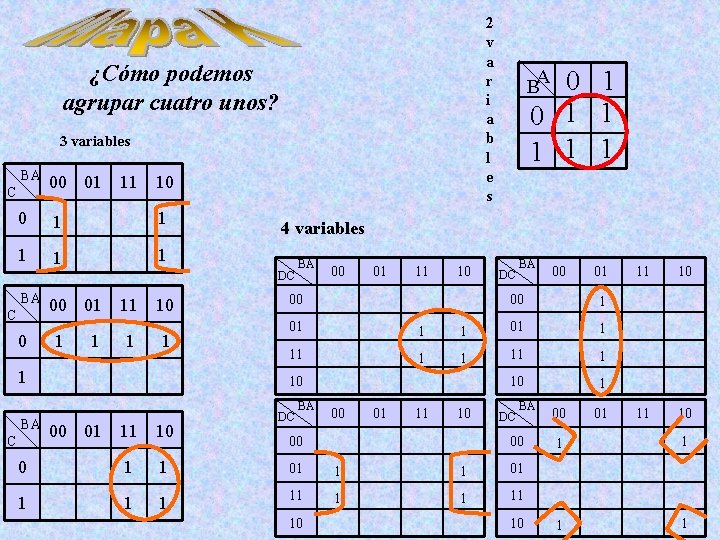
2 v a r i a b l e s ¿Cómo podemos agrupar cuatro unos? 3 variables BA C 00 01 11 10 0 1 1 1 4 variables DC BA C 0 00 01 11 10 1 1 1 BA C BA 00 01 11 10 00 DC BA 00 01 00 1 01 1 11 1 10 00 01 11 10 0 1 1 1 BA DC BA 00 01 11 10 00 DC BA 00 0 1 1 01 1 11 10 10 00 01 11 10 1 1

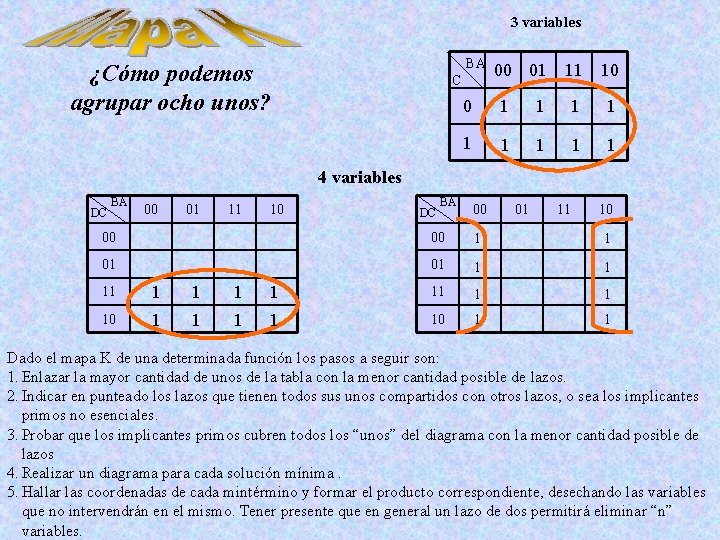
3 variables BA ¿Cómo podemos agrupar ocho unos? C 00 01 11 10 0 1 1 1 1 1 4 variables DC BA 00 01 11 10 00 00 1 1 01 01 1 1 11 1 1 10 1 1 Dado el mapa K de una determinada función los pasos a seguir son: 1. Enlazar la mayor cantidad de unos de la tabla con la menor cantidad posible de lazos. 2. Indicar en punteado los lazos que tienen todos sus unos compartidos con otros lazos, o sea los implicantes primos no esenciales. 3. Probar que los implicantes primos cubren todos los “unos” del diagrama con la menor cantidad posible de lazos 4. Realizar un diagrama para cada solución mínima. 5. Hallar las coordenadas de cada mintérmino y formar el producto correspondiente, desechando las variables que no intervendrán en el mismo. Tener presente que en general un lazo de dos permitirá eliminar “n” variables.

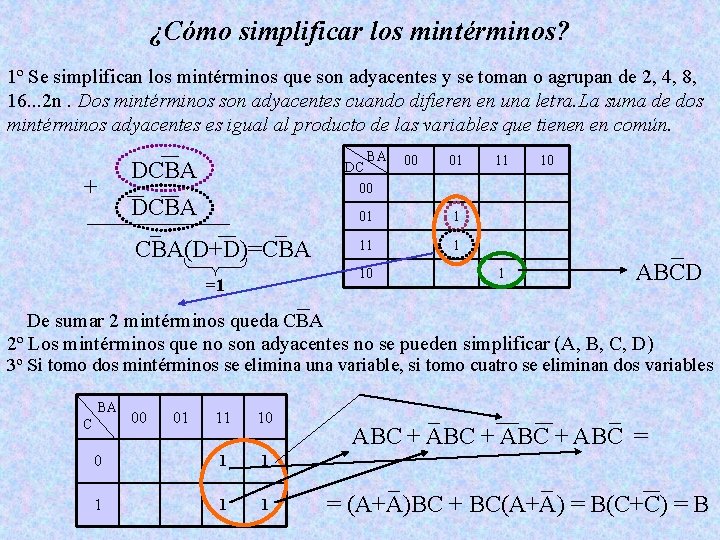
¿Cómo simplificar los mintérminos? 1º Se simplifican los mintérminos que son adyacentes y se toman o agrupan de 2, 4, 8, 16. . . 2 n. Dos mintérminos son adyacentes cuando difieren en una letra. La suma de dos mintérminos adyacentes es igual al producto de las variables que tienen en común. BA DC 00 DCBA + DCBA CBA(D+D)=CBA 01 01 1 10 =1 00 11 1 10 ABCD De sumar 2 mintérminos queda CBA 2º Los mintérminos que no son adyacentes no se pueden simplificar (A, B, C, D) 3º Si tomo dos mintérminos se elimina una variable, si tomo cuatro se eliminan dos variables BA 11 10 0 1 1 1 C 00 01 ABC + ABC = = (A+A)BC + BC(A+A) = B(C+C) = B

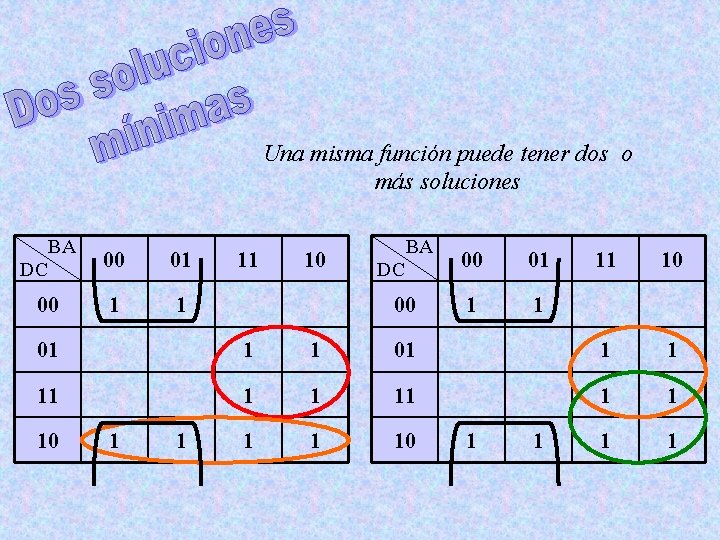
Una misma función puede tener dos o más soluciones BA DC 00 00 01 1 1 11 10 01 1 1 11 1 10 1 1

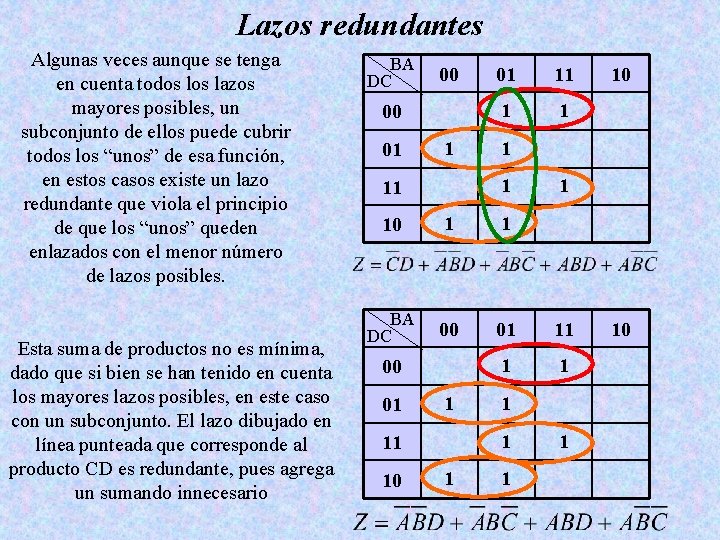
Lazos redundantes Algunas veces aunque se tenga en cuenta todos lazos mayores posibles, un subconjunto de ellos puede cubrir todos los “unos” de esa función, en estos casos existe un lazo redundante que viola el principio de que los “unos” queden enlazados con el menor número de lazos posibles. Esta suma de productos no es mínima, dado que si bien se han tenido en cuenta los mayores lazos posibles, en este caso con un subconjunto. El lazo dibujado en línea punteada que corresponde al producto CD es redundante, pues agrega un sumando innecesario BA DC 00 00 01 11 1 10 1 1 BA DC 00 01 11 1 1 00 01 1 10

Cuando una variable de salida no se puede definir con un cero o con un uno en la tabla de verdad se coloca una “x” que significa redundancia o “no preocuparse” Esto sucede cuando no nos interesa la función de salida o cuando se trata de estados prohibidos que no forman parte de algún código. La redundancia se puede usar como un comodín, se puede tomar como uno o cero individualmente

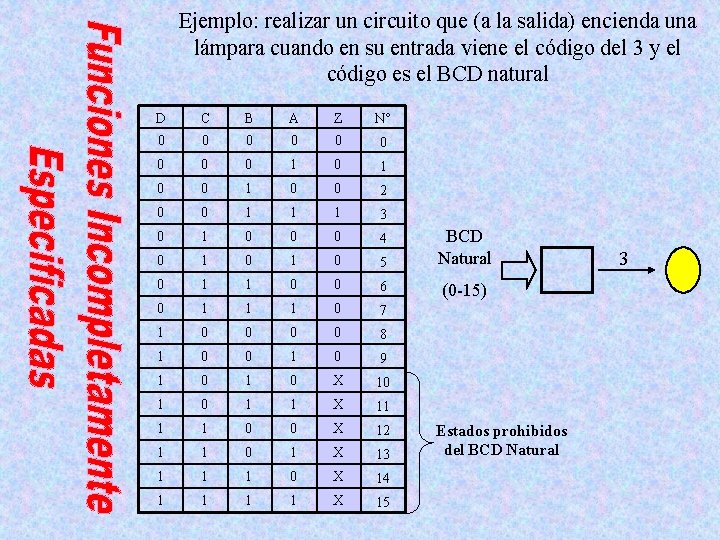
Ejemplo: realizar un circuito que (a la salida) encienda una lámpara cuando en su entrada viene el código del 3 y el código es el BCD natural D C B A Z N° 0 0 0 0 0 1 0 0 2 0 0 1 1 1 3 0 1 0 0 0 4 0 1 0 5 BCD Natural 0 1 1 0 0 6 (0 -15) 0 1 1 1 0 7 1 0 0 8 1 0 0 1 0 9 1 0 X 10 1 1 X 11 1 1 0 0 X 12 1 1 0 1 X 13 1 1 1 0 X 14 1 1 X 15 Estados prohibidos del BCD Natural 3

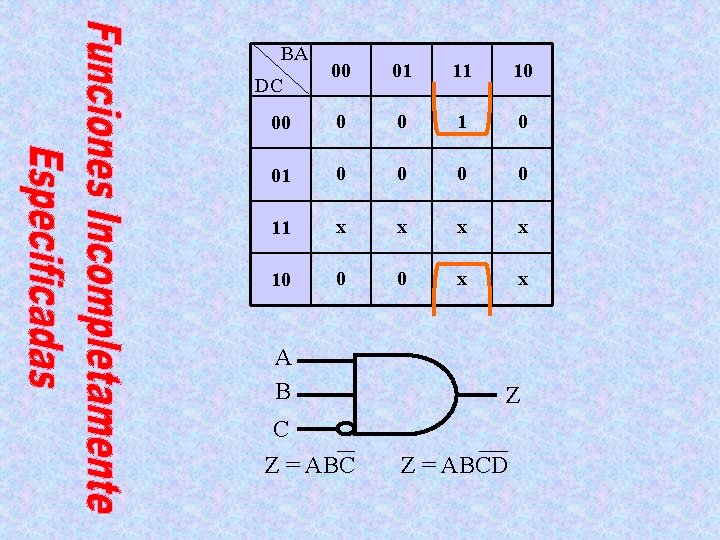
BA 00 01 11 10 00 0 0 1 0 0 0 0 11 x x 10 0 0 x x DC A B Z C Z = ABCD

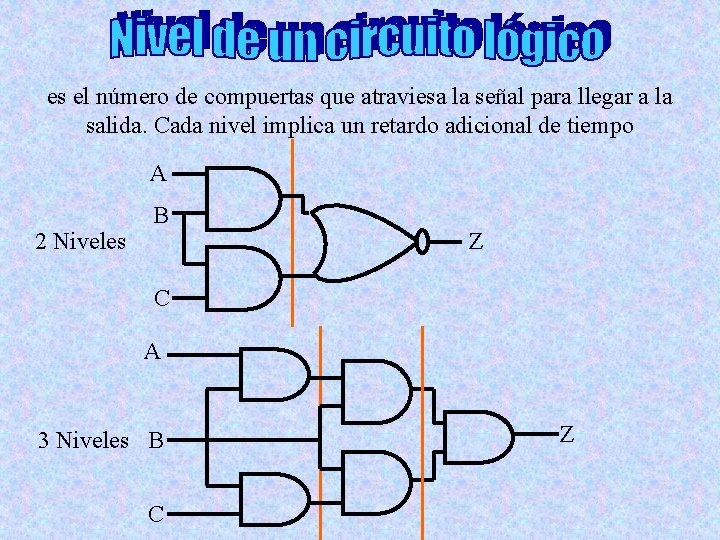
es el número de compuertas que atraviesa la señal para llegar a la salida. Cada nivel implica un retardo adicional de tiempo A 2 Niveles B Z C A 3 Niveles B C Z

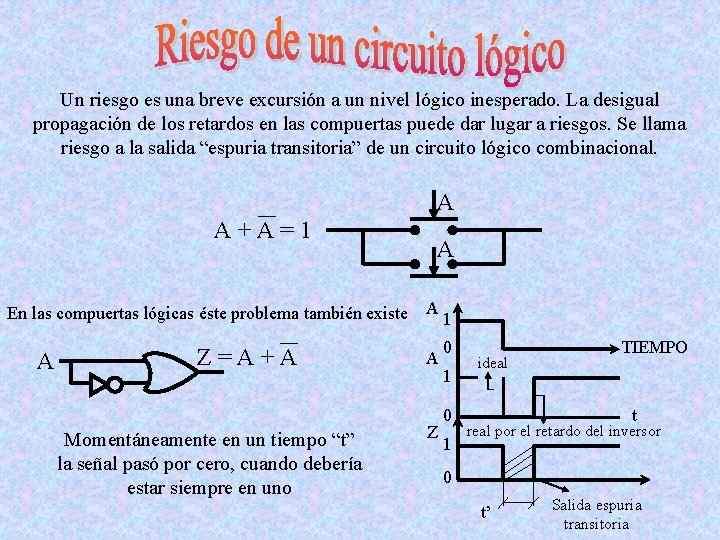
Un riesgo es una breve excursión a un nivel lógico inesperado. La desigual propagación de los retardos en las compuertas puede dar lugar a riesgos. Se llama riesgo a la salida “espuria transitoria” de un circuito lógico combinacional. A A+A=1 A En las compuertas lógicas éste problema también existe A 1 A Z=A+A Momentáneamente en un tiempo “t” la señal pasó por cero, cuando debería estar siempre en uno A Z 0 1 ideal TIEMPO t real por el retardo del inversor 0 t’ Salida espuria transitoria

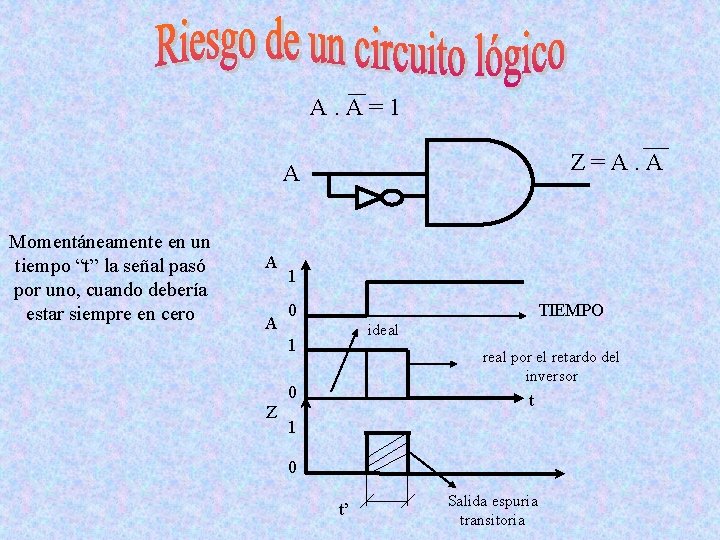
A. A=1 Z=A. A A Momentáneamente en un tiempo “t” la señal pasó por uno, cuando debería estar siempre en cero A A 1 0 TIEMPO ideal 1 real por el retardo del inversor 0 Z t 1 0 t’ Salida espuria transitoria

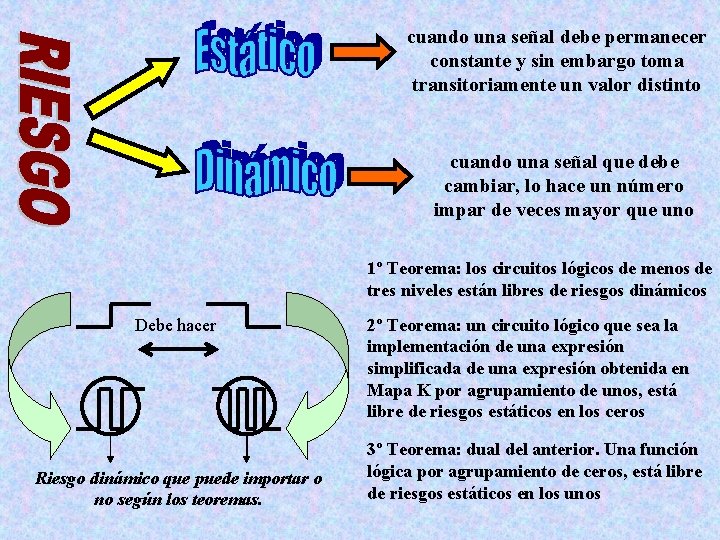
cuando una señal debe permanecer constante y sin embargo toma transitoriamente un valor distinto cuando una señal que debe cambiar, lo hace un número impar de veces mayor que uno 1º Teorema: los circuitos lógicos de menos de tres niveles están libres de riesgos dinámicos Debe hacer Riesgo dinámico que puede importar o no según los teoremas. 2º Teorema: un circuito lógico que sea la implementación de una expresión simplificada de una expresión obtenida en Mapa K por agrupamiento de unos, está libre de riesgos estáticos en los ceros 3º Teorema: dual del anterior. Una función lógica por agrupamiento de ceros, está libre de riesgos estáticos en los unos

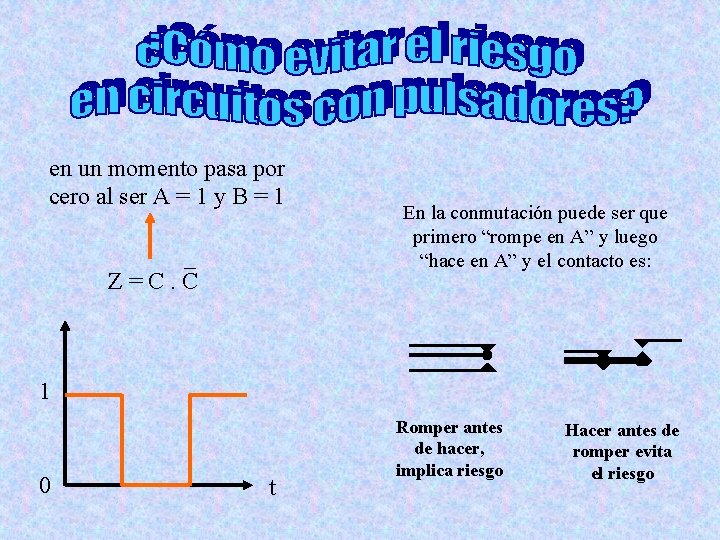
en un momento pasa por cero al ser A = 1 y B = 1 Z=C. C En la conmutación puede ser que primero “rompe en A” y luego “hace en A” y el contacto es: 1 0 t Romper antes de hacer, implica riesgo Hacer antes de romper evita el riesgo

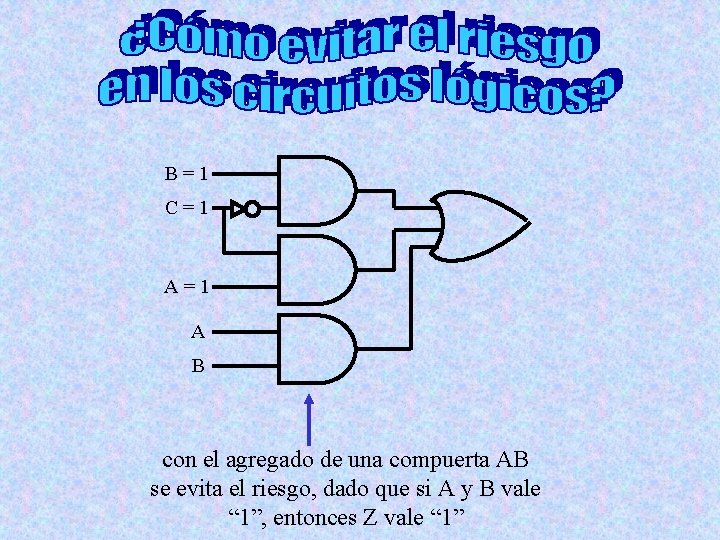
B=1 C=1 A B con el agregado de una compuerta AB se evita el riesgo, dado que si A y B vale “ 1”, entonces Z vale “ 1”

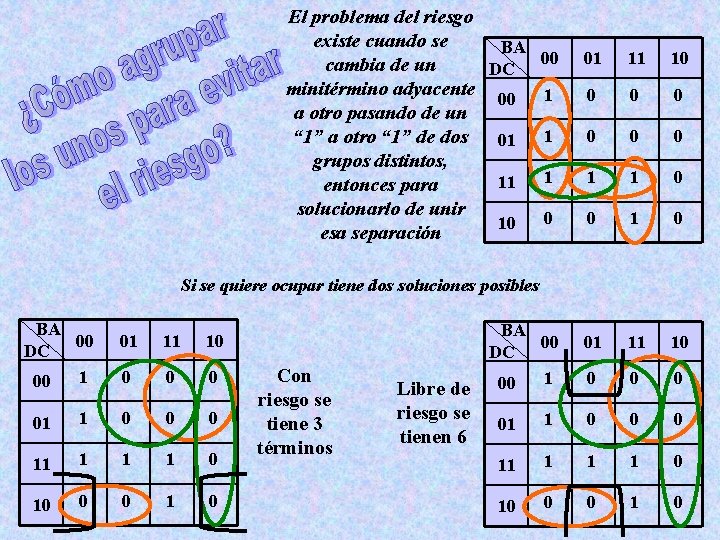
El problema del riesgo existe cuando se BA cambia de un DC minitérmino adyacente 00 a otro pasando de un “ 1” a otro “ 1” de dos 01 grupos distintos, 11 entonces para solucionarlo de unir 10 esa separación 00 01 11 10 1 0 0 0 1 1 1 0 0 0 1 0 01 11 10 0 Si se quiere ocupar tiene dos soluciones posibles BA 00 DC 1 00 01 11 10 0 01 1 0 0 0 11 1 0 10 0 0 1 0 Con riesgo se tiene 3 términos Libre de riesgo se tienen 6 BA 00 DC 1 00 01 1 0 0 0 11 1 0 10 0 0 1 0

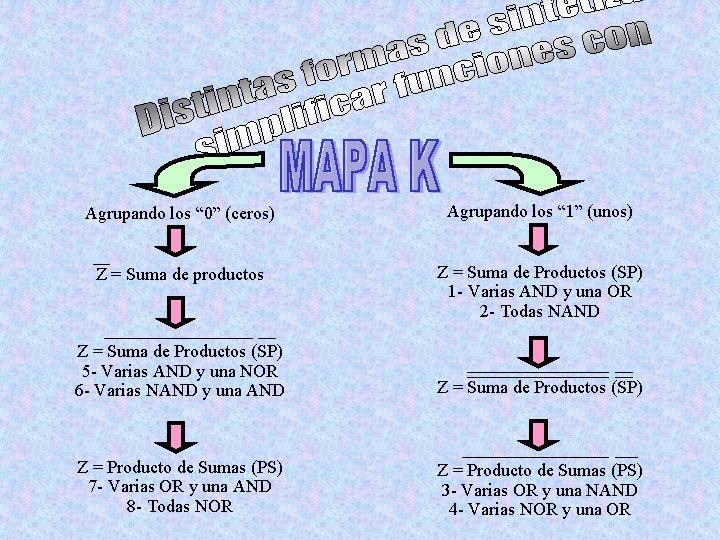
Agrupando los “ 0” (ceros) Agrupando los “ 1” (unos) Z = Suma de productos Z = Suma de Productos (SP) 1 - Varias AND y una OR 2 - Todas NAND Z = Suma de Productos (SP) 5 - Varias AND y una NOR 6 - Varias NAND y una AND Z = Suma de Productos (SP) Z = Producto de Sumas (PS) 7 - Varias OR y una AND 8 - Todas NOR Z = Producto de Sumas (PS) 3 - Varias OR y una NAND 4 - Varias NOR y una OR

A A B B Z Z A A C C AND OR NAND

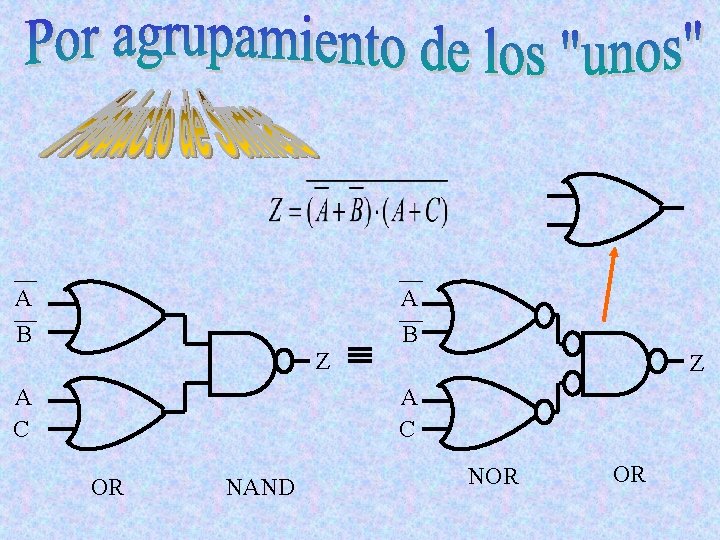
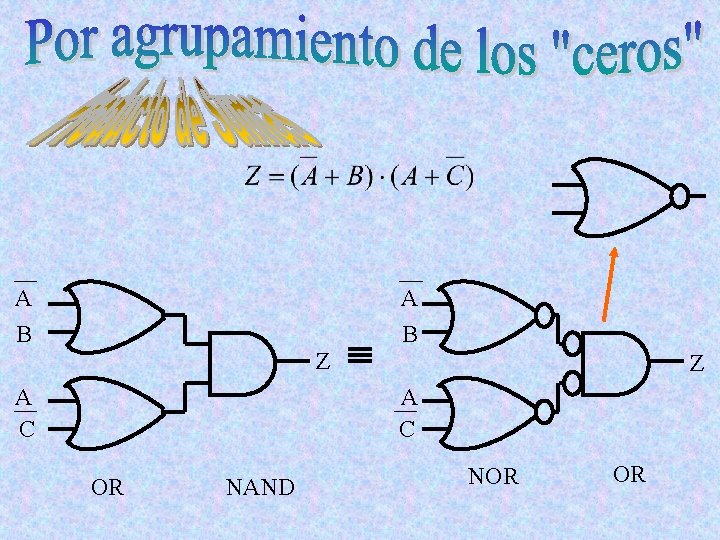
A B Z A C OR NAND NOR OR

A A B B Z Z A A C C AND NOR NAND

A B Z A C OR NAND NOR OR