Support Vector Machines Note to other teachers and

Support Vector Machines Note to other teachers and users of these slides. Andrew would be delighted if you found this source material useful in giving your own lectures. Feel free to use these slides verbatim, or to modify them to fit your own needs. Power. Point originals are available. If you make use of a significant portion of these slides in your own lecture, please include this message, or the following link to the source repository of Andrew’s tutorials: http: //www. cs. cmu. edu/~awm/tutorials. Comments and corrections gratefully received. Andrew W. Moore Professor School of Computer Science Carnegie Mellon University www. cs. cmu. edu/~awm awm@cs. cmu. edu 412 -268 -7599 Copyright © 2001, 2003, Andrew W. Moore Nov 23 rd, 2001

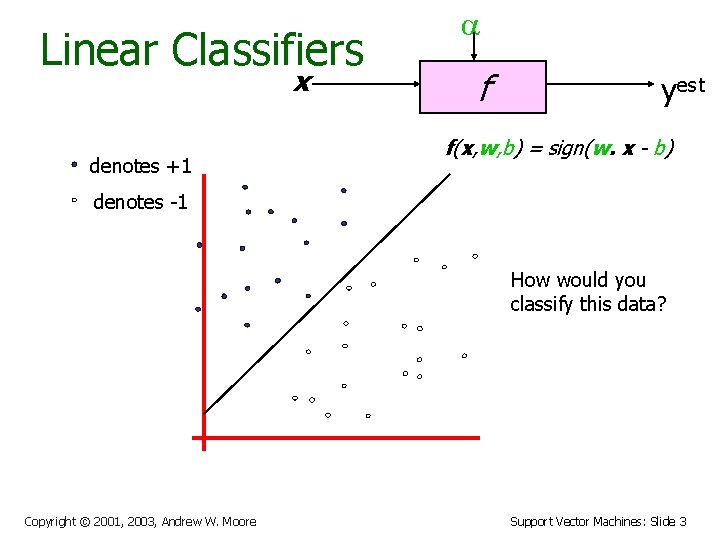
Linear Classifiers x denotes +1 a f yest f(x, w, b) = sign(w. x - b) denotes -1 How would you classify this data? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 2

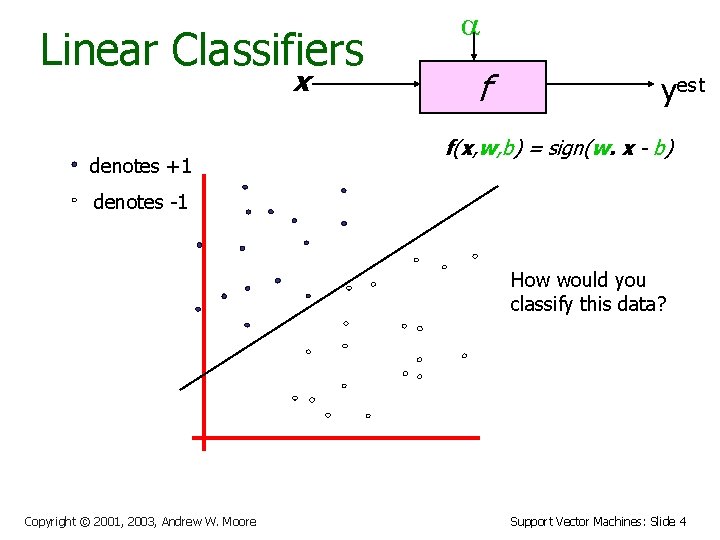
Linear Classifiers x denotes +1 a f yest f(x, w, b) = sign(w. x - b) denotes -1 How would you classify this data? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 3

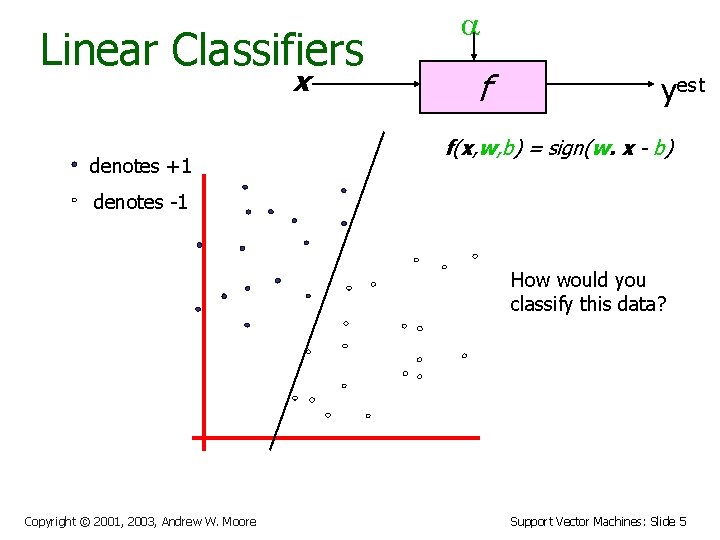
Linear Classifiers x denotes +1 a f yest f(x, w, b) = sign(w. x - b) denotes -1 How would you classify this data? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 4

Linear Classifiers x denotes +1 a f yest f(x, w, b) = sign(w. x - b) denotes -1 How would you classify this data? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 5

Linear Classifiers x denotes +1 a f yest f(x, w, b) = sign(w. x - b) denotes -1 Any of these would be fine. . but which is best? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 6

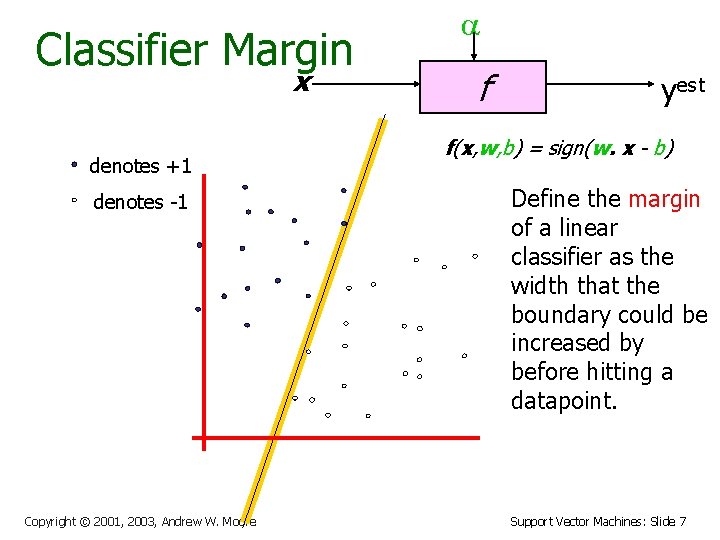
Classifier Margin x denotes +1 denotes -1 Copyright © 2001, 2003, Andrew W. Moore a f yest f(x, w, b) = sign(w. x - b) Define the margin of a linear classifier as the width that the boundary could be increased by before hitting a datapoint. Support Vector Machines: Slide 7

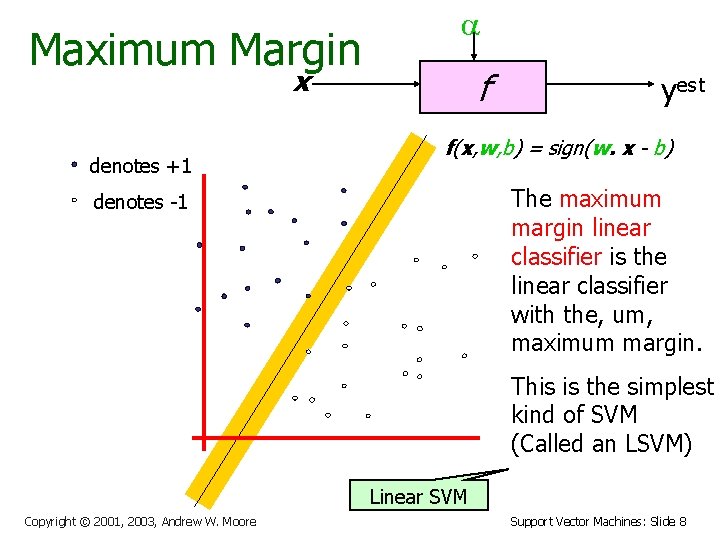
Maximum Margin a x denotes +1 f yest f(x, w, b) = sign(w. x - b) The maximum margin linear classifier is the linear classifier with the, um, maximum margin. denotes -1 This is the simplest kind of SVM (Called an LSVM) Linear SVM Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 8

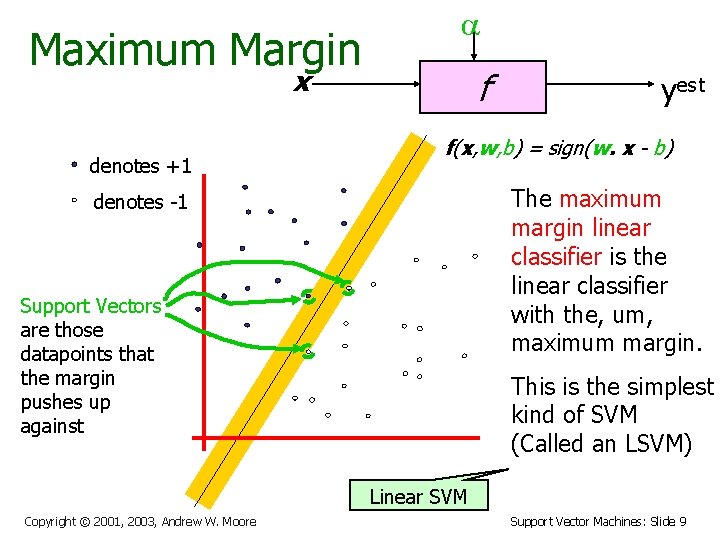
Maximum Margin a x denotes +1 f yest f(x, w, b) = sign(w. x - b) The maximum margin linear classifier is the linear classifier with the, um, maximum margin. denotes -1 Support Vectors are those datapoints that the margin pushes up against This is the simplest kind of SVM (Called an LSVM) Linear SVM Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 9

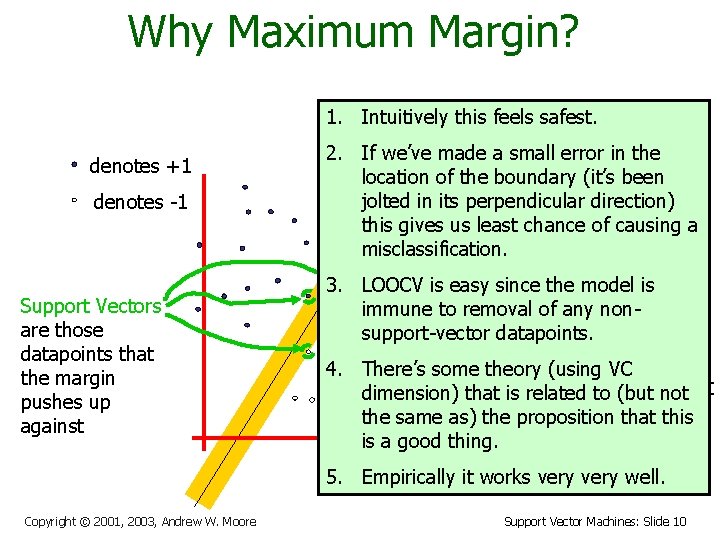
Why Maximum Margin? 1. Intuitively this feels safest. denotes +1 denotes -1 Support Vectors are those datapoints that the margin pushes up against f(x, w, b) = sign(w. - b) 2. If we’ve made a small error inxthe location of the boundary (it’s been The maximum jolted in its perpendicular direction) this gives us leastmargin chance linear of causing a misclassification. classifier is the 3. LOOCV is easy since the classifier model is linear immune to removal of any with the, nonum, support-vector datapoints. maximum margin. 4. There’s some theory (using VC is the simplest dimension) that is. This related to (but not of SVM the same as) thekind proposition that this is a good thing. (Called an LSVM) 5. Empirically it works very well. Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 10

Specifying a line and margin ” 1 + = ss a l t C one c i z ed r P “ Plus-Plane Classifier Boundary 1” = Minus-Plane ss a l t C one c i z red “P • How do we represent this mathematically? • …in m input dimensions? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 11

Specifying a line and margin ” 1 + = Plus-Plane Classifier Boundary ss a l t C one c i z ed r P “ =1 b + 0 wx b= + wx b=-1 + wx 1” = Minus-Plane ss a l t C one c i z red “P • Plus-plane = { x : w. x + b = +1 } • Minus-plane = { x : w. x + b = -1 } if w. x + b >= 1 -1 if w. x + b <= -1 Universe explodes if -1 < w. x + b < 1 Classify as. . +1 Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 12

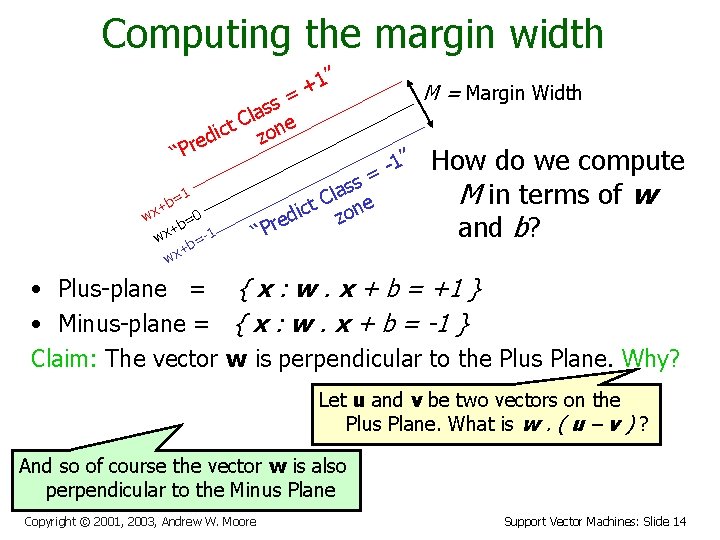
Computing the margin width ” 1 + = ss a l t C one c i z ed r P “ =1 b + 0 wx b= + wx b=-1 + wx M = Margin Width 1” = “P ss a l t C one c i z red How do we compute M in terms of w and b? • Plus-plane = { x : w. x + b = +1 } • Minus-plane = { x : w. x + b = -1 } Claim: The vector w is perpendicular to the Plus Plane. Why? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 13

Computing the margin width ” 1 + = ss a l t C one c i z ed r P “ =1 b + 0 wx b= + wx b=-1 + wx M = Margin Width 1” = ss a l t C one c i z red “P How do we compute M in terms of w and b? • Plus-plane = { x : w. x + b = +1 } • Minus-plane = { x : w. x + b = -1 } Claim: The vector w is perpendicular to the Plus Plane. Why? Let u and v be two vectors on the Plus Plane. What is w. ( u – v ) ? And so of course the vector w is also perpendicular to the Minus Plane Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 14

Computing the margin width 1” + + M = Margin Width = x s s la e C ct zon i d e “Pr 1” How do we compute x = s s la M in terms of w =1 C b e t + wx dic zon =0 e b r + and b? “P -1 wx = +b x w • • • Plus-plane = { x : w. x + b = +1 } Minus-plane = { x : w. x + b = -1 } The vector w is perpendicular to the Plus Plane Let x- be any point on the minus plane Let x+ be the closest plus-plane-point to x-. Copyright © 2001, 2003, Andrew W. Moore Any location in mm: : not R necessarily a datapoint Support Vector Machines: Slide 15

Computing the margin width 1” + + M = Margin Width = = x s s la e C ct zon i d e “Pr 1” x = s s la =1 C b e t + c n i 0 o wx d z = re M = |x+ - x- | =| l w |= +b -1 P x “ w = +b x w What we know: • w. x+ + b = +1 • w. x- + b = -1 • x+ = x- + l w • |x + - x - | = M • Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 16

Learning the Maximum Margin Classifier ” M = Given guess of 1 + = “P +b =1 wx ss a l t C one c i z red 0 b= + wx b=-1 + wx 1” = ss a l t C one c i z ed r P “ What should our quadratic optimization criterion be? Copyright © 2001, 2003, Andrew W. Moore w , b we can • Compute whether all data points are in the correct half-planes • Compute the margin width Assume R datapoints, each (xk, yk) where yk = +/- 1 How many constraints will we have? What should they be? Support Vector Machines: Slide 17

Learning the Maximum Margin Classifier ” M = Given guess of 1 + = “P +b =1 wx ss a l t C one c i z red 0 b= + wx b=-1 + wx 1” = ss a l t C one c i z ed r P “ What should our quadratic optimization criterion be? Minimize w. w w , b we can • Compute whether all data points are in the correct half-planes • Compute the margin width Assume R datapoints, each (xk, yk) where yk = +/- 1 How many constraints will we have? R What should they be? w. xk + b >= 1 if yk = 1 w. xk + b <= -1 if yk = -1 Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 18

What You Should Know • Linear SVMs • The definition of a maximum margin classifier • What QP can do for you (but, for this class, you don’t need to know how it does it) • How Maximum Margin can be turned into a QP problem • How we deal with noisy (non-separable) data • How we permit non-linear boundaries • How SVM Kernel functions permit us to pretend we’re working with ultra-high-dimensional basisfunction terms Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 19