Support Vector Machines Note to other teachers and



















































- Slides: 84

Support Vector Machines Note to other teachers and users of these slides. Andrew would be delighted if you found this source material useful in giving your own lectures. Feel free to use these slides verbatim, or to modify them to fit your own needs. Power. Point originals are available. If you make use of a significant portion of these slides in your own lecture, please include this message, or the following link to the source repository of Andrew’s tutorials: http: //www. cs. cmu. edu/~awm/tutorials. Comments and corrections gratefully received. Andrew W. Moore Professor School of Computer Science Carnegie Mellon University www. cs. cmu. edu/~awm awm@cs. cmu. edu 412 -268 -7599 Copyright © 2001, 2003, Andrew W. Moore Nov 23 rd, 2001

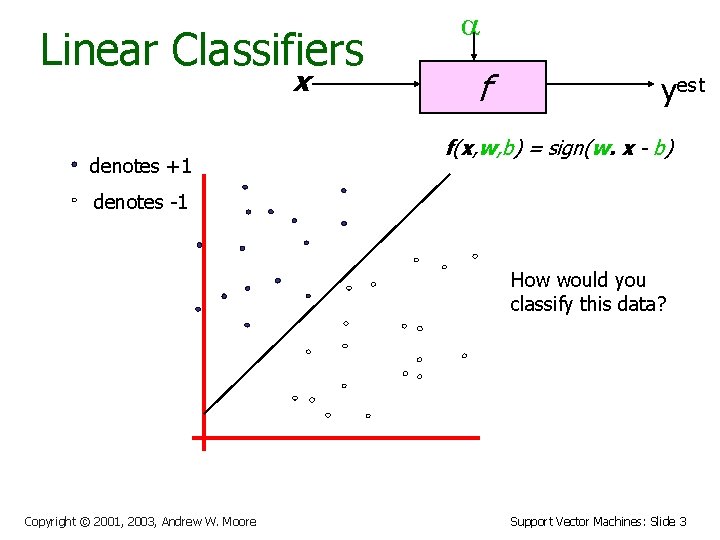
Linear Classifiers x denotes +1 f yest f(x, w, b) = sign(w. x - b) denotes -1 How would you classify this data? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 2

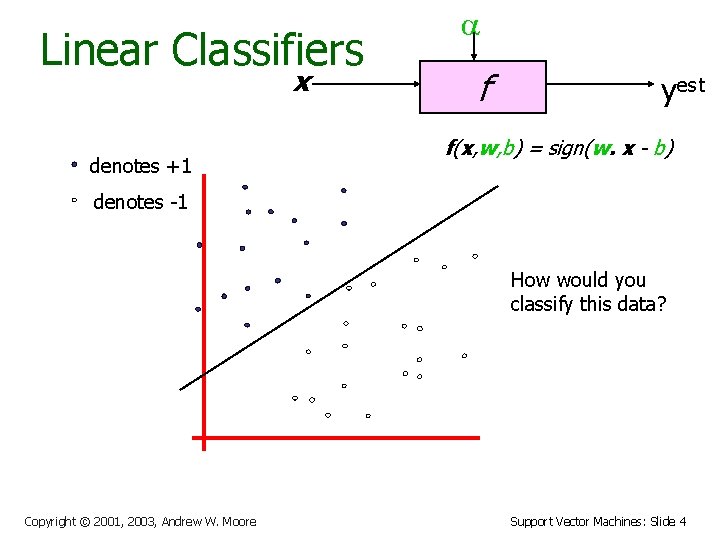
Linear Classifiers x denotes +1 f yest f(x, w, b) = sign(w. x - b) denotes -1 How would you classify this data? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 3

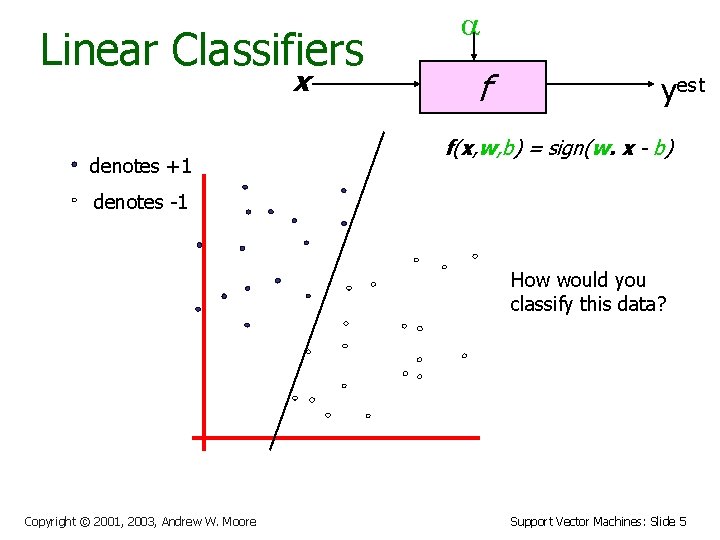
Linear Classifiers x denotes +1 f yest f(x, w, b) = sign(w. x - b) denotes -1 How would you classify this data? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 4

Linear Classifiers x denotes +1 f yest f(x, w, b) = sign(w. x - b) denotes -1 How would you classify this data? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 5

Linear Classifiers x denotes +1 f yest f(x, w, b) = sign(w. x - b) denotes -1 Any of these would be fine. . but which is best? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 6

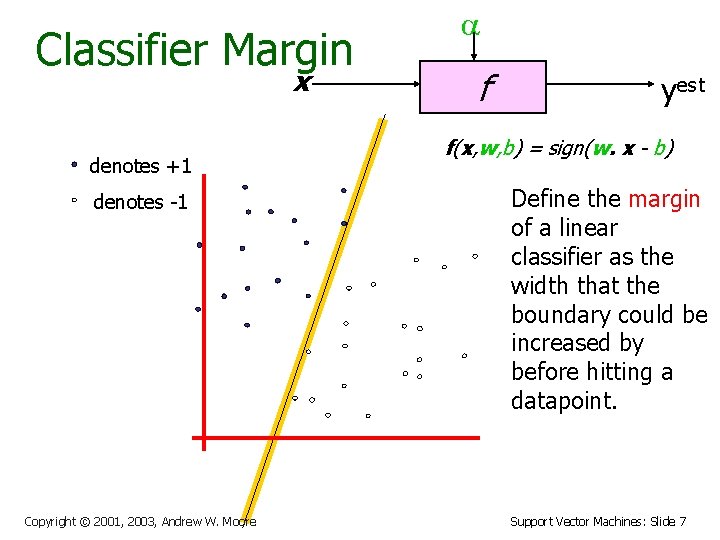
Classifier Margin x denotes +1 denotes -1 Copyright © 2001, 2003, Andrew W. Moore f yest f(x, w, b) = sign(w. x - b) Define the margin of a linear classifier as the width that the boundary could be increased by before hitting a datapoint. Support Vector Machines: Slide 7

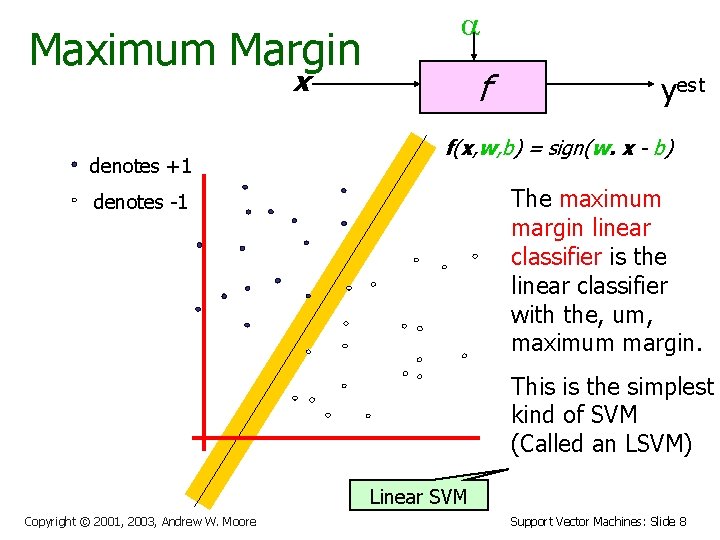
Maximum Margin x denotes +1 f yest f(x, w, b) = sign(w. x - b) The maximum margin linear classifier is the linear classifier with the, um, maximum margin. denotes -1 This is the simplest kind of SVM (Called an LSVM) Linear SVM Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 8

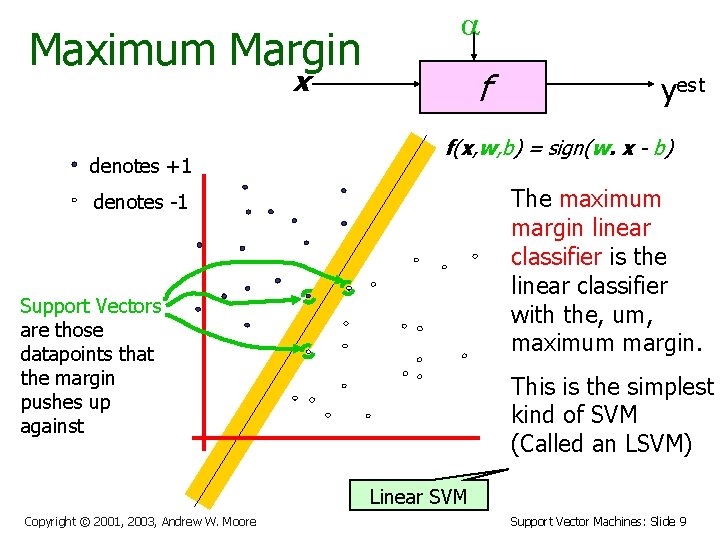
Maximum Margin x denotes +1 f yest f(x, w, b) = sign(w. x - b) The maximum margin linear classifier is the linear classifier with the, um, maximum margin. denotes -1 Support Vectors are those datapoints that the margin pushes up against This is the simplest kind of SVM (Called an LSVM) Linear SVM Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 9

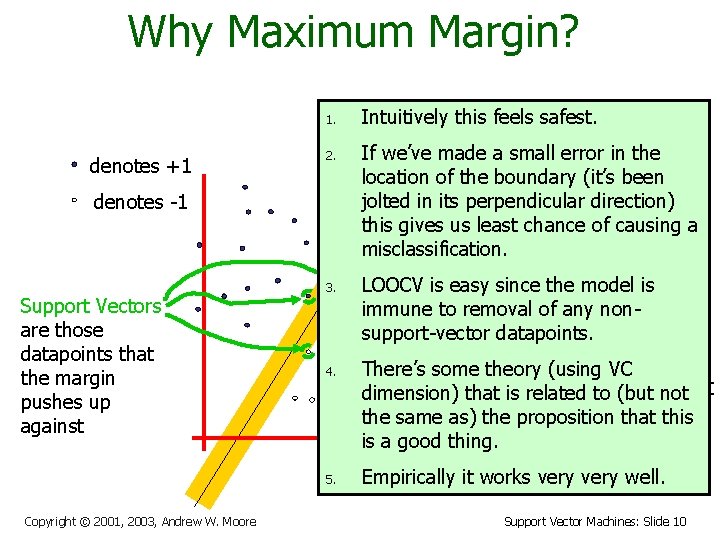
Why Maximum Margin? 1. denotes +1 2. denotes -1 Support Vectors are those datapoints that the margin pushes up against 3. f(x, w, b) = sign(w. - b) If we’ve made a small error inxthe location of the boundary (it’s been The maximum jolted in its perpendicular direction) this gives us leastmargin chance linear of causing a misclassification. classifier is the LOOCV is easy since the classifier model is linear immune to removal of any with the, nonum, support-vector datapoints. maximum margin. 4. 5. Copyright © 2001, 2003, Andrew W. Moore Intuitively this feels safest. There’s some theory (using VC is the simplest dimension) that is. This related to (but not of SVM the same as) thekind proposition that this is a good thing. (Called an LSVM) Empirically it works very well. Support Vector Machines: Slide 10

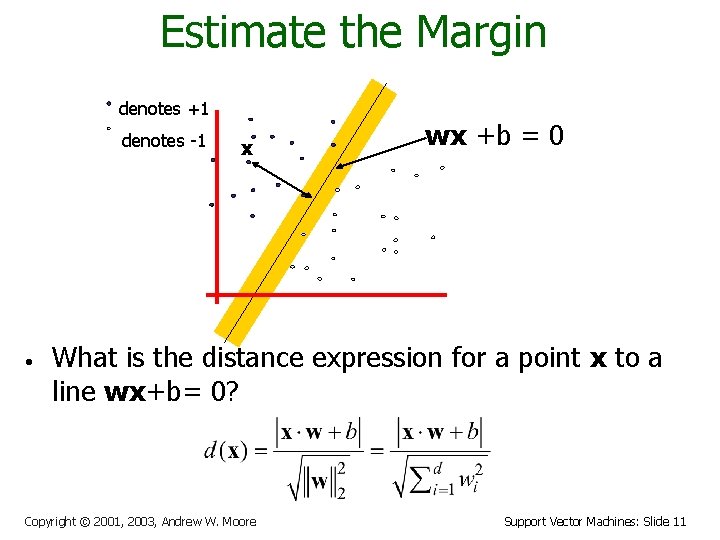
Estimate the Margin denotes +1 denotes -1 • x wx +b = 0 What is the distance expression for a point x to a line wx+b= 0? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 11

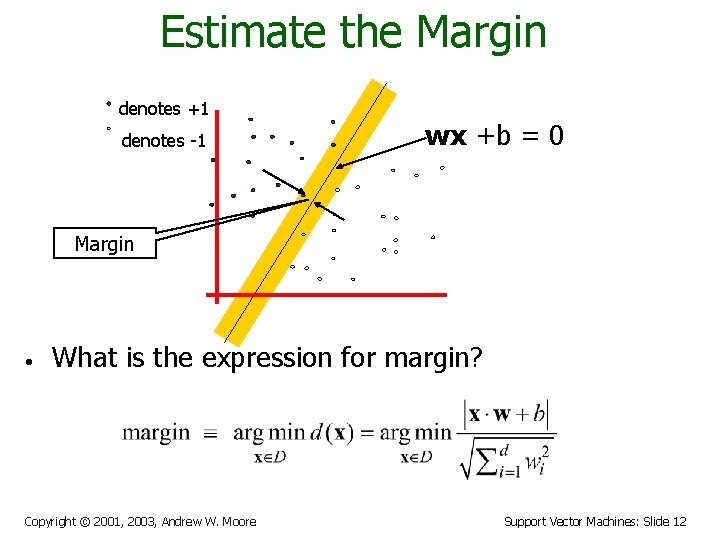
Estimate the Margin denotes +1 denotes -1 wx +b = 0 Margin • What is the expression for margin? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 12

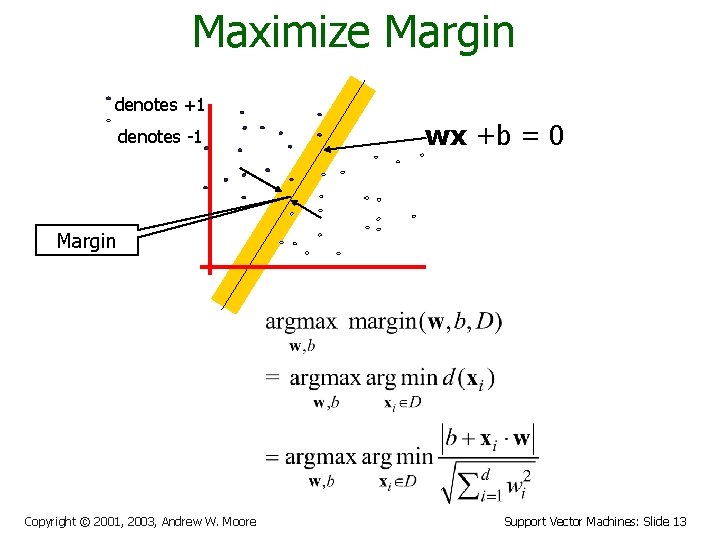
Maximize Margin denotes +1 denotes -1 wx +b = 0 Margin Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 13

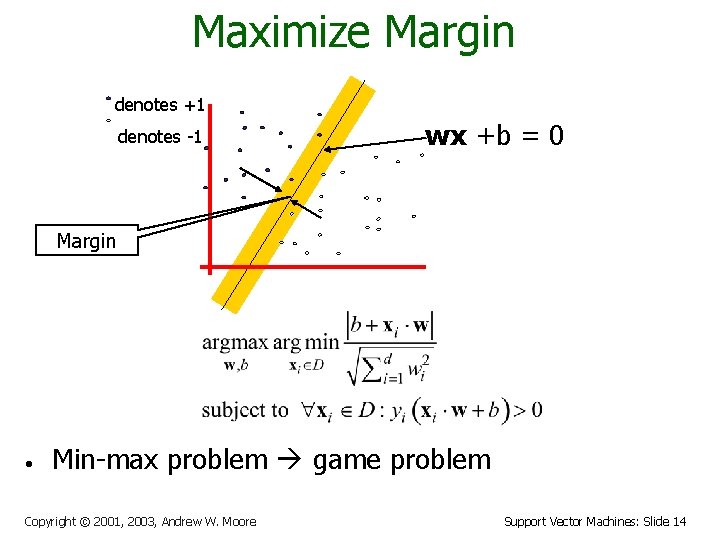
Maximize Margin denotes +1 denotes -1 wx +b = 0 Margin • Min-max problem game problem Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 14

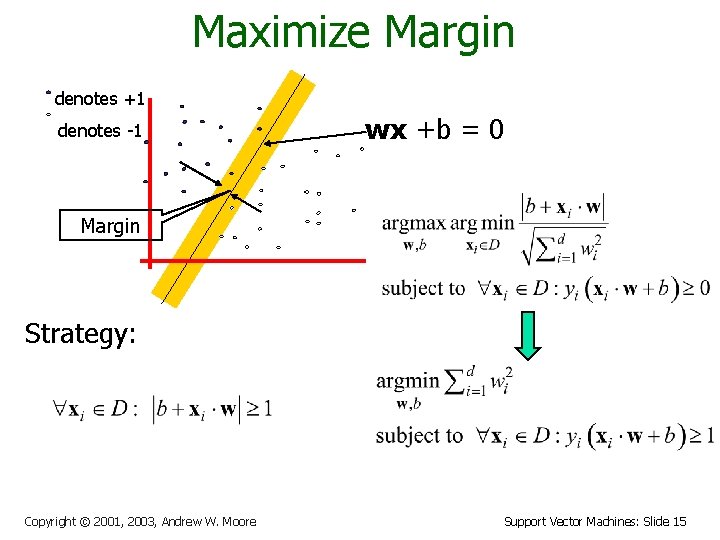
Maximize Margin denotes +1 denotes -1 wx +b = 0 Margin Strategy: Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 15

Maximum Margin Linear Classifier • How to solve it? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 16

Learning via Quadratic Programming • QP is a well-studied class of optimization algorithms to maximize a quadratic function of some real-valued variables subject to linear constraints. Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 17

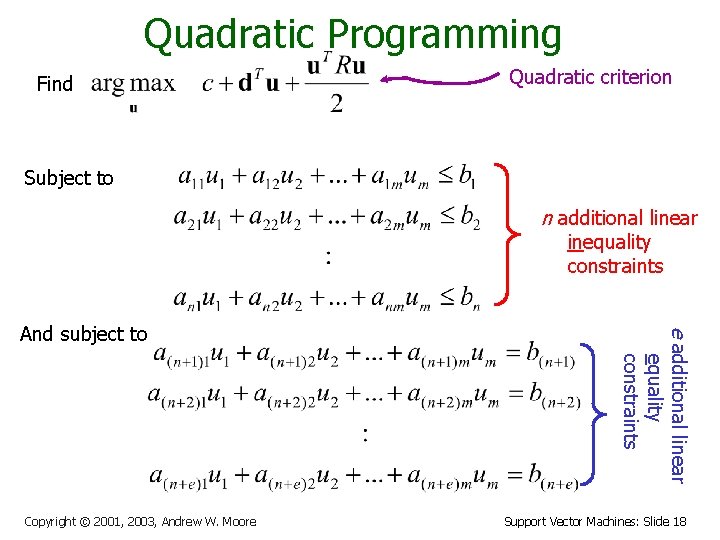
Quadratic Programming Find Quadratic criterion Subject to n additional linear inequality constraints Copyright © 2001, 2003, Andrew W. Moore e additional linear equality constraints And subject to Support Vector Machines: Slide 18

Quadratic Programming Quadratic criterion Find Subject to Copyright © 2001, 2003, Andrew W. Moore n additional linear inequality constraints e additional linear equality constraints And subject to ding n i f r o f thms i r o g l a ratic d t a s i u x q e ned i a There r t s ently n i o c i c f f h e c su more h c u ent i m d a a r m g i t op than y l b a i l and re ascent. you … y l d d i ery f v ite e r r w a o y t e t (But th ly don’t wan elf) s r probab u o y one Support Vector Machines: Slide 19

Quadratic Programming Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 20

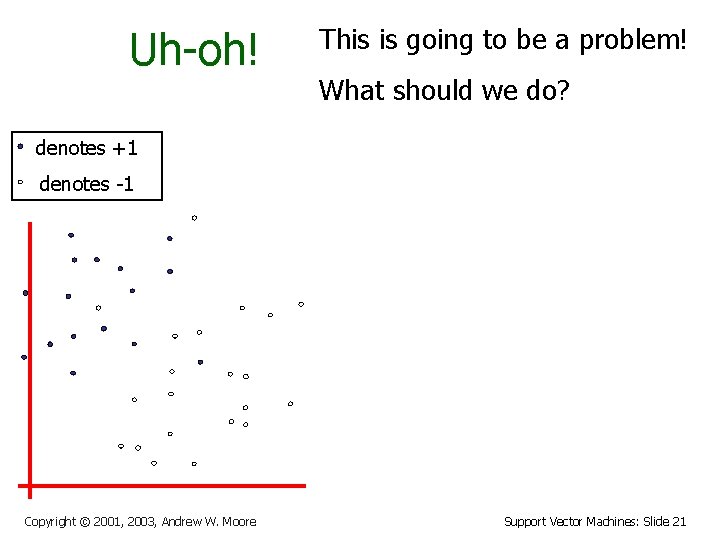
Uh-oh! This is going to be a problem! What should we do? denotes +1 denotes -1 Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 21

Uh-oh! denotes +1 denotes -1 This is going to be a problem! What should we do? Idea 1: Find minimum w. w, while minimizing number of training set errors. Problemette: Two things to minimize makes for an ill-defined optimization Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 22

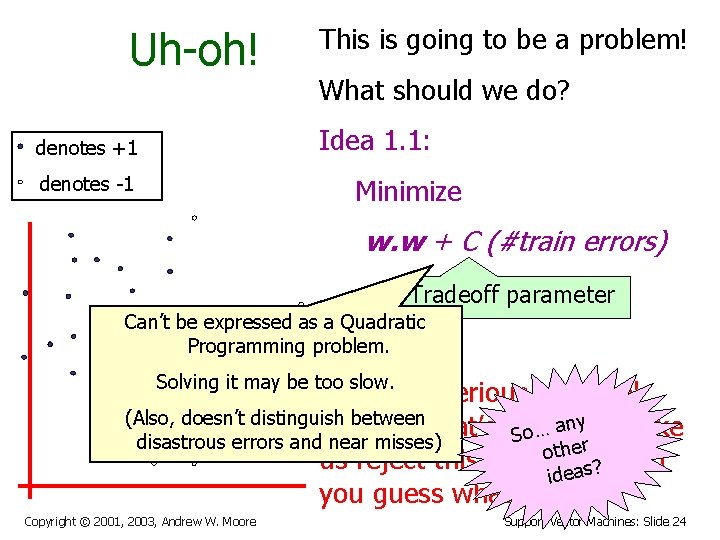
Uh-oh! denotes +1 denotes -1 This is going to be a problem! What should we do? Idea 1. 1: Minimize w. w + C (#train errors) Tradeoff parameter There’s a serious practical problem that’s about to make us reject this approach. Can you guess what it is? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 23

Uh-oh! This is going to be a problem! What should we do? Idea 1. 1: denotes +1 denotes -1 Minimize w. w + C (#train errors) Tradeoff parameter Can’t be expressed as a Quadratic Programming problem. Solving it may be too slow. There’s a serious practical (Also, doesn’t distinguish between problem that’s about … anyto make o S disastrous errors and near misses) ther o us reject this approach. Can ideas? you guess what it is? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 24

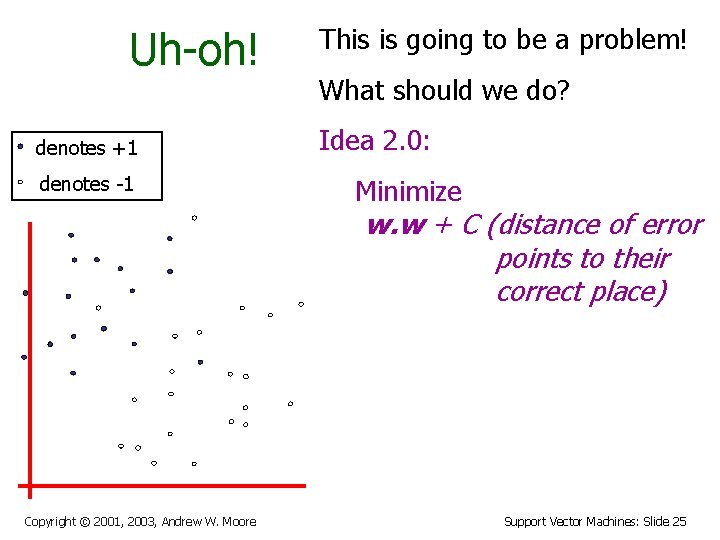
Uh-oh! denotes +1 denotes -1 This is going to be a problem! What should we do? Idea 2. 0: Minimize w. w + C (distance of error points to their correct place) Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 25

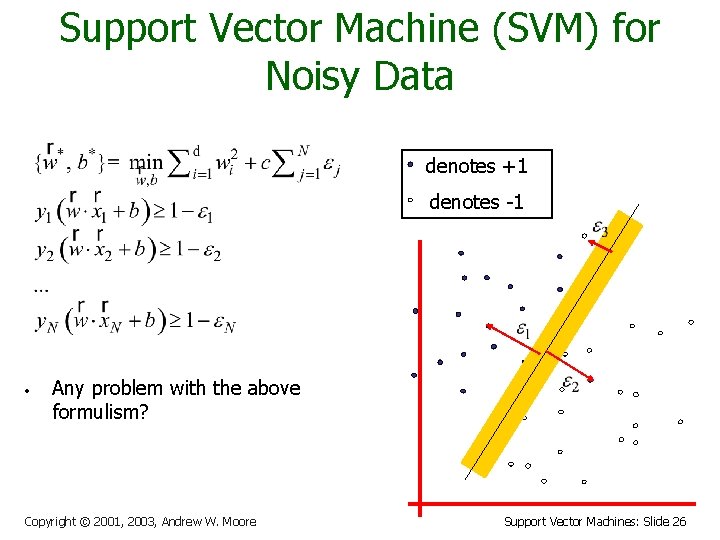
Support Vector Machine (SVM) for Noisy Data denotes +1 denotes -1 • Any problem with the above formulism? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 26

Support Vector Machine (SVM) for Noisy Data denotes +1 denotes -1 • Balance the trade off between margin and classification errors Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 27

Support Vector Machine for Noisy Data How do we determine the appropriate value for c ? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 28

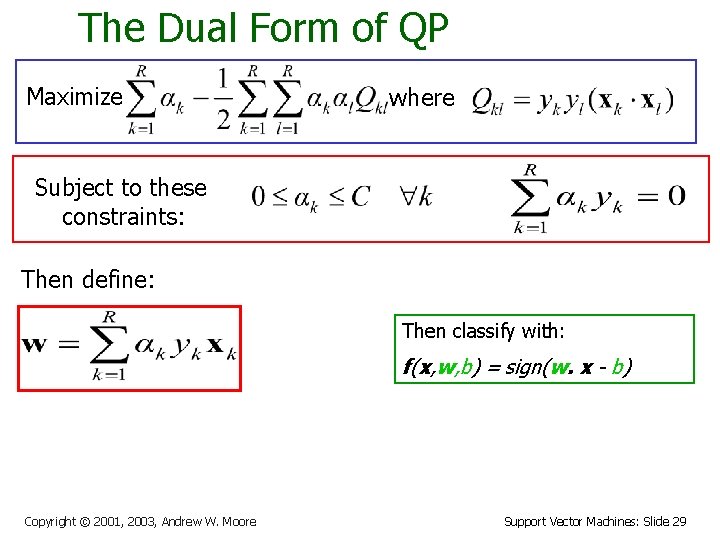
The Dual Form of QP Maximize where Subject to these constraints: Then define: Then classify with: f(x, w, b) = sign(w. x - b) Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 29

The Dual Form of QP Maximize where Subject to these constraints: Then define: Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 30

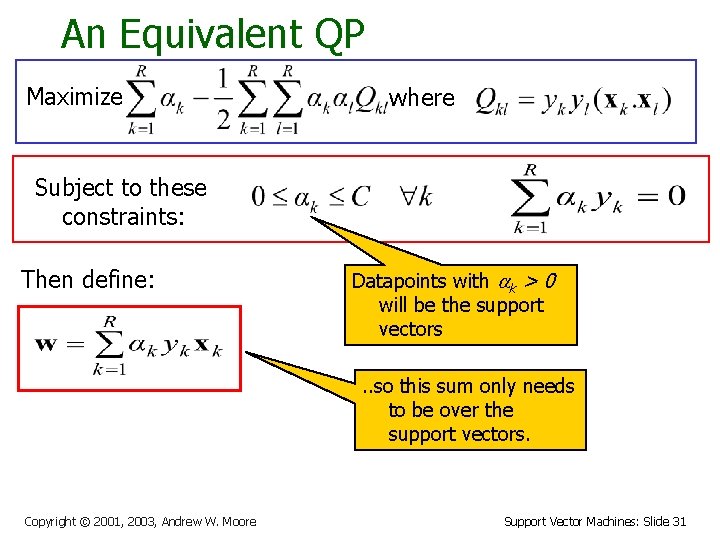
An Equivalent QP Maximize where Subject to these constraints: Then define: Datapoints with ak > 0 will be the support vectors. . so this sum only needs to be over the support vectors. Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 31

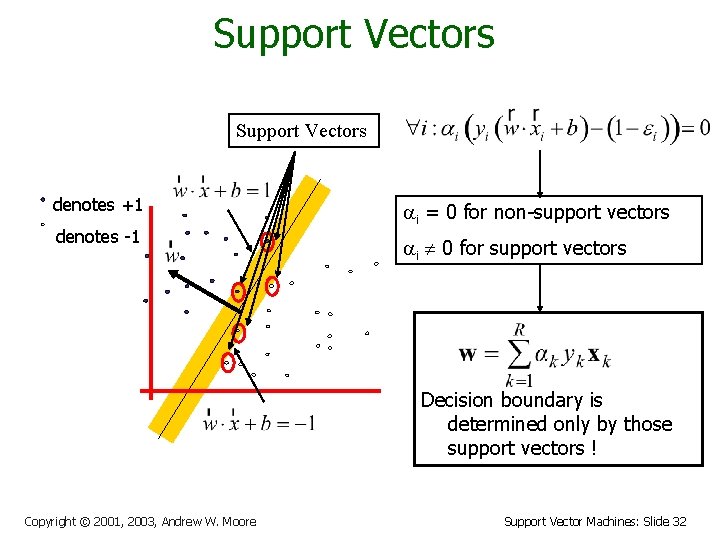
Support Vectors denotes +1 denotes -1 i = 0 for non-support vectors i 0 for support vectors Decision boundary is determined only by those support vectors ! Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 32

The Dual Form of QP Maximize where Subject to these constraints: Then define: Then classify with: f(x, w, b) = sign(w. x - b) How to determine b ? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 33

An Equivalent QP: Determine b Fix w A linear programming problem ! Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 34

An Equivalent QP Maximize where Why did I tell you about this Subject to these equivalent QP? constraints: • It’s a formulation that QP packages can optimize more Then define: Datapoints with ak > 0 quickly • will be the support vectors Then classify with: further jaw- Because of dropping developments f(x, w, b)you’re = sign(w. x - b) about to learn. . . so this sum only needs to be over the support vectors. Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 35

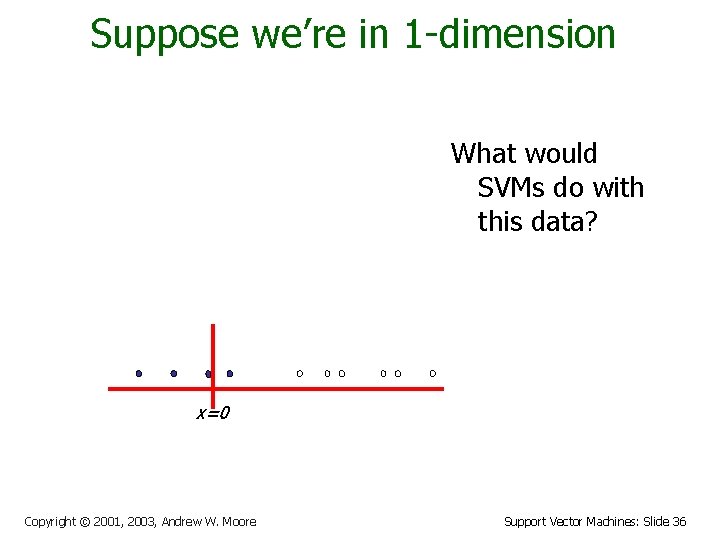
Suppose we’re in 1 -dimension What would SVMs do with this data? x=0 Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 36

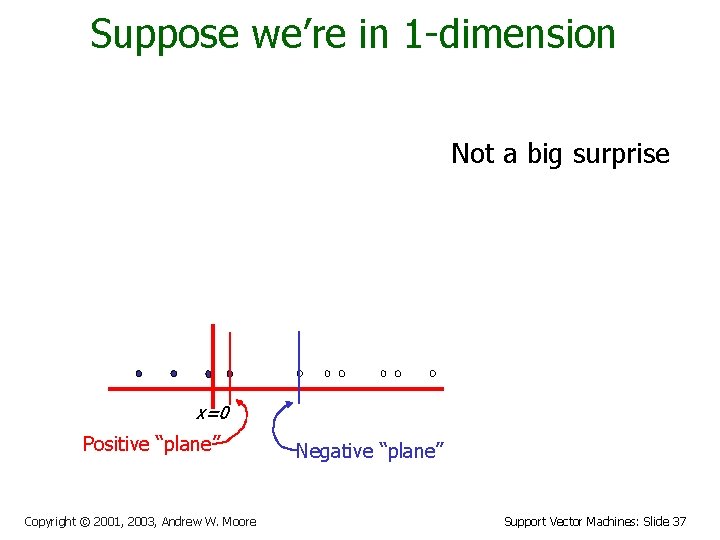
Suppose we’re in 1 -dimension Not a big surprise x=0 Positive “plane” Copyright © 2001, 2003, Andrew W. Moore Negative “plane” Support Vector Machines: Slide 37

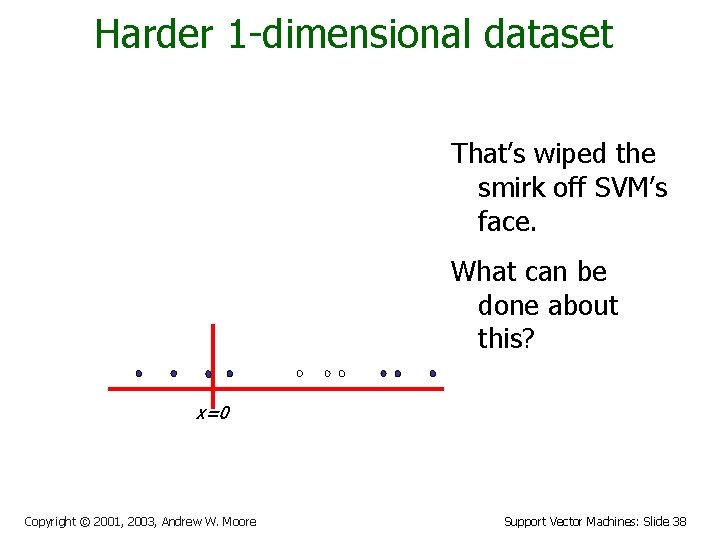
Harder 1 -dimensional dataset That’s wiped the smirk off SVM’s face. What can be done about this? x=0 Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 38

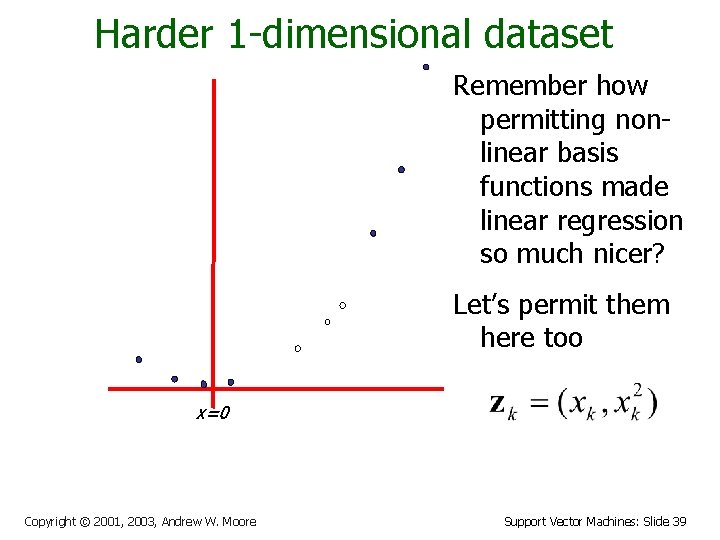
Harder 1 -dimensional dataset Remember how permitting nonlinear basis functions made linear regression so much nicer? Let’s permit them here too x=0 Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 39

Harder 1 -dimensional dataset Remember how permitting nonlinear basis functions made linear regression so much nicer? Let’s permit them here too x=0 Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 40

Common SVM basis functions zk = ( polynomial terms of xk of degree 1 to q ) zk = ( radial basis functions of xk ) zk = ( sigmoid functions of xk ) This is sensible. Is that the end of the story? No…there’s one more trick! Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 41

Quadratic Basis Functions Constant Term Linear Terms Number of terms (assuming m input dimensions) = (m+2)-choose-2 Pure Quadratic Terms = (m+2)(m+1)/2 = (as near as makes no difference) m 2/2 You may be wondering what those Quadratic Cross-Terms ’s are doing. You should be happy that they do no harm • You’ll find out why they’re there soon. • Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 42

QP (old) Maximize where Subject to these constraints: Then define: Then classify with: f(x, w, b) = sign(w. x - b) Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 43

QP with basis functions Maximize where Subject to these constraints: Then define: Then classify with: f(x, w, b) = sign(w. f(x) - b) Most important changes: X f(x) Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 44

QP with basis functions Maximize Subject to these constraints: Then define: where We must do R 2/2 dot products to get this matrix ready. Each dot product requires m 2/2 additions and multiplications The whole thing costs R 2 m 2 /4. Yeeks! …or does it? Then classify with: f(x, w, b) = sign(w. f(x) - b) Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 45

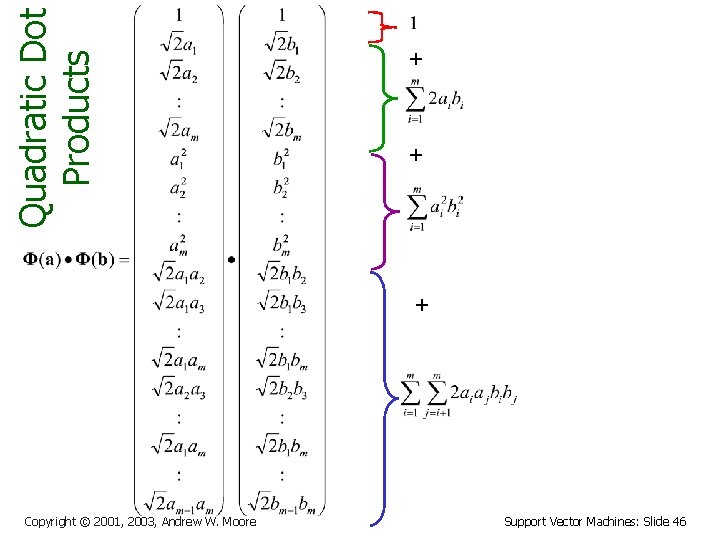
Quadratic Dot Products + + + Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 46

Quadratic Dot Products Copyright © 2001, 2003, Andrew W. Moore Just out of casual, innocent, interest, let’s look at another function of a and b: Support Vector Machines: Slide 47

Quadratic Dot Products Just out of casual, innocent, interest, let’s look at another function of a and b: They’re the same! And this is only O(m) to compute! Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 48

QP with Quadratic basis functions Maximize Subject to these constraints: Then define: where We must do R 2/2 dot products to get this matrix ready. Each dot product now only requires m additions and multiplications Then classify with: f(x, w, b) = sign(w. f(x) - b) Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 49

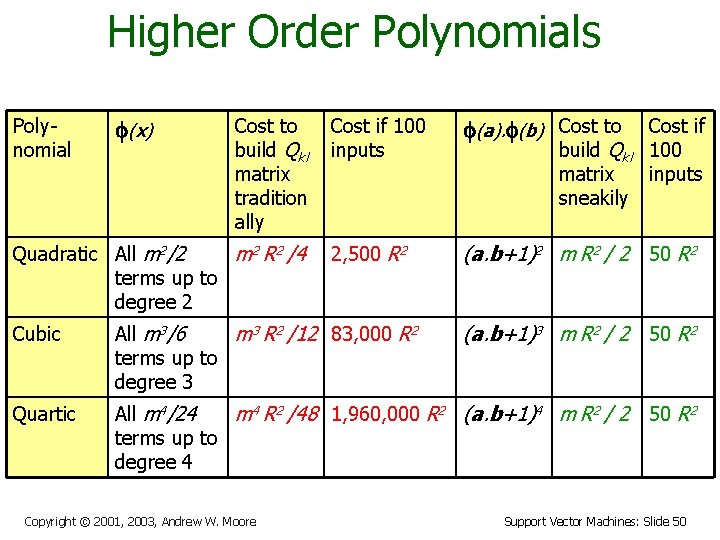
Higher Order Polynomials Polynomial f(x) Cost to build Qkl matrix tradition ally Quadratic All m 2/2 m 2 R 2 /4 terms up to degree 2 Cost if 100 inputs f(a). f(b) Cost to 2, 500 R 2 (a. b+1)2 m R 2 / 2 50 R 2 build Qkl matrix sneakily Cubic All m 3/6 m 3 R 2 /12 83, 000 R 2 terms up to degree 3 Quartic All m 4/24 m 4 R 2 /48 1, 960, 000 R 2 (a. b+1)4 m R 2 / 2 terms up to degree 4 Copyright © 2001, 2003, Andrew W. Moore Cost if 100 inputs (a. b+1)3 m R 2 / 2 50 R 2 Support Vector Machines: Slide 50

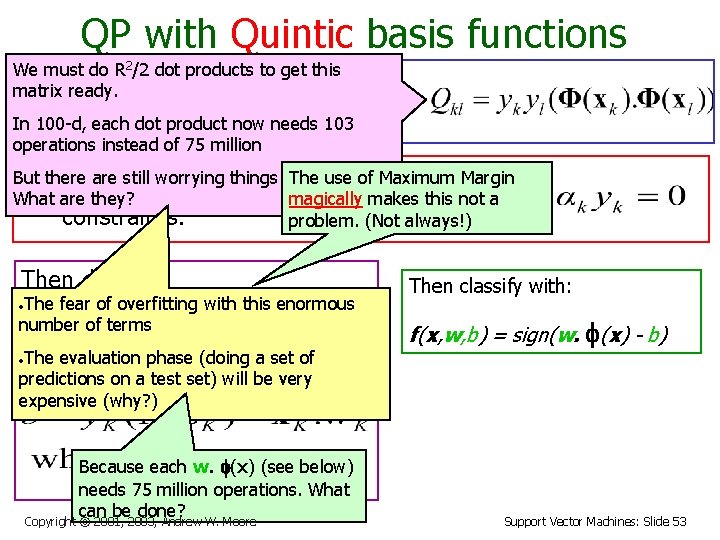
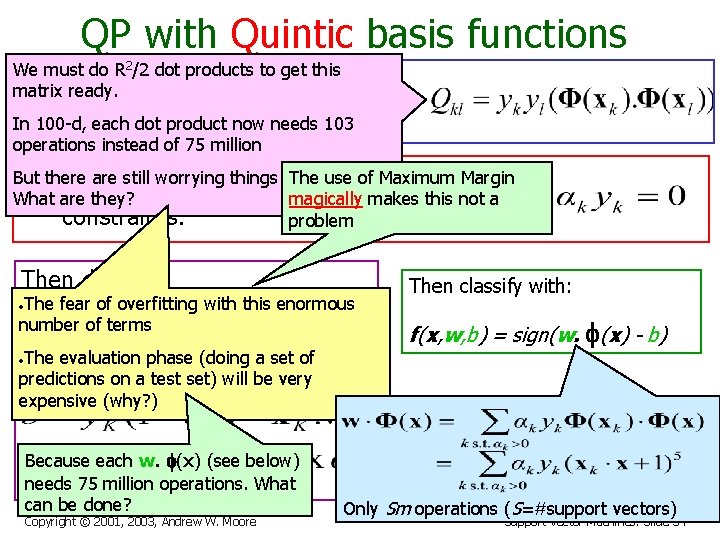
QP with Quintic basis functions We must do R 2/2 dot products to get this matrix ready. Maximize where In 100 -d, each dot product now needs 103 operations instead of 75 million But there are still worrying things lurking away. Subject to What are they? these constraints: Then define: Then classify with: f(x, w, b) = sign(w. f(x) - b) Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 51

QP with Quintic basis functions We must do R 2/2 dot products to get this matrix ready. Maximize where In 100 -d, each dot product now needs 103 operations instead of 75 million But there are still worrying things lurking away. Subject to these What are they? constraints: Then define: • The fear of overfitting with this enormous number of terms Then classify with: f(x, w, b) = sign(w. f(x) - b) • The evaluation phase (doing a set of predictions on a test set) will be very expensive (why? ) Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 52

QP with Quintic basis functions We must do R 2/2 dot products to get this matrix ready. Maximize where In 100 -d, each dot product now needs 103 operations instead of 75 million But there are still worrying things lurking away. The use of Maximum Margin Subject to these What are they? magically makes this not a constraints: problem. (Not always!) Then define: • The fear of overfitting with this enormous number of terms • The evaluation phase (doing a set of predictions on a test set) will be very expensive (why? ) Because each w. f(x) (see below) needs 75 million operations. What can be done? Copyright © 2001, 2003, Andrew W. Moore Then classify with: f(x, w, b) = sign(w. f(x) - b) Support Vector Machines: Slide 53

QP with Quintic basis functions We must do R 2/2 dot products to get this matrix ready. Maximize where In 100 -d, each dot product now needs 103 operations instead of 75 million But there are still worrying things lurking away. The use of Maximum Margin Subject to these What are they? magically makes this not a constraints: problem Then define: • The fear of overfitting with this enormous number of terms • The evaluation phase (doing a set of predictions on a test set) will be very expensive (why? ) Because each w. f(x) (see below) needs 75 million operations. What can be done? Copyright © 2001, 2003, Andrew W. Moore Then classify with: f(x, w, b) = sign(w. f(x) - b) Only Sm operations (S=#support vectors) Support Vector Machines: Slide 54

QP with Quintic basis functions Maximize where Subject to these constraints: Then define: Then classify with: f(x, w, b) = sign(w. f(x) - b) Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 55

QP with Quadratic basis functions Maximize where Subject to these constraints: Then define: Then classify with: f(x, w, b) = sign(K(w, x) - b) Most important change: Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 56

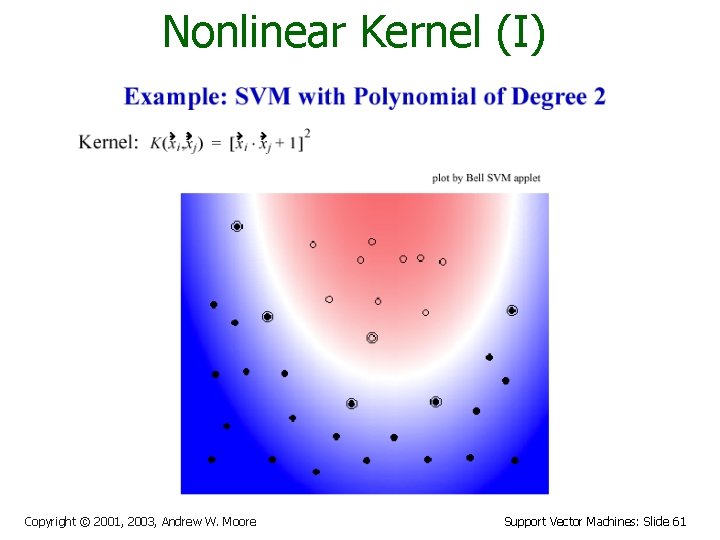
SVM Kernel Functions • • K(a, b)=(a. b +1)d is an example of an SVM Kernel Function Beyond polynomials there are other very high dimensional basis functions that can be made practical by finding the right Kernel Function • Radial-Basis-style Kernel Function: • Neural-net-style Kernel Function: Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 57

Kernel Tricks • • Replacing dot product with a kernel function Not all functions are kernel functions • Need to be decomposable • K(a, b) = (a) (b) • Could K(a, b) = (a-b)3 be a kernel function ? • Could K(a, b) = (a-b)4 – (a+b)2 be a kernel function? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 58

Kernel Tricks • Mercer’s condition To expand Kernel function K(x, y) into a dot product, i. e. K(x, y)= (x) (y), K(x, y) has to be positive semi-definite function, i. e. , for any function f(x) whose is finite, the following inequality holds • Could Copyright © 2001, 2003, Andrew W. Moore be a kernel function? Support Vector Machines: Slide 59

Kernel Tricks • • Pro • Introducing nonlinearity into the model • Computational cheap Con • Still have potential overfitting problems Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 60

Nonlinear Kernel (I) Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 61

Nonlinear Kernel (II) Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 62

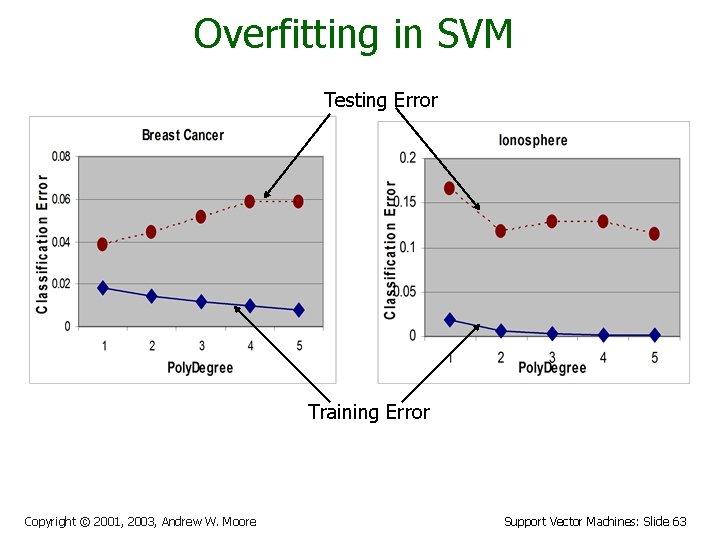
Overfitting in SVM Testing Error Training Error Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 63

SVM Performance • • • Anecdotally they work very well indeed. Example: They are currently the best-known classifier on a well-studied hand-written-character recognition benchmark Another Example: Andrew knows several reliable people doing practical real-world work who claim that SVMs have saved them when their other favorite classifiers did poorly. There is a lot of excitement and religious fervor about SVMs as of 2001. Despite this, some practitioners are a little skeptical. Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 64

Kernelize Logistic Regression How can we introduce the nonlinearity into the logistic regression? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 65

Kernelize Logistic Regression • Representation Theorem Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 66

Diffusion Kernel • • • Kernel function describes the correlation or similarity between two data points Given that I have a function s(x, y) that describes the similarity between two data points. Assume that it is a nonnegative and symmetric function. How can we generate a kernel function based on this similarity function? A graph theory approach … Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 67

Diffusion Kernel • Create a graph for the data points • Each vertex corresponds to a data point • The weight of each edge is the similarity s(x, y) • • Graph Laplacian Properties of Laplacian • Negative semi-definite Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 68

Diffusion Kernel • • • Consider a simple Laplacian Consider • What do these matrixes represent? A diffusion kernel Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 69

Diffusion Kernel • • • Consider a simple Laplacian Consider • What do these matrixes represent? A diffusion kernel Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 70

Diffusion Kernel: Properties • • Positive definite Local relationships L induce global relationships Works for undirected weighted graphs with similarities How to compute the diffusion kernel Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 71

Computing Diffusion Kernel • Singular value decomposition of Laplacian L • What is L 2 ? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 72

Computing Diffusion Kernel • What about Ln ? • Compute diffusion kernel Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 73

Doing multi-classification • • • SVMs can only handle two-class outputs (i. e. a categorical output variable with arity 2). What can be done? Answer: with output arity N, learn N SVM’s • • • SVM 1 learns “Output==1” vs “Output != 1” SVM 2 learns “Output==2” vs “Output != 2” : SVM N learns “Output==N” vs “Output != N” Then to predict the output for a new input, just predict with each SVM and find out which one puts the prediction the furthest into the positive region. Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 74

References • An excellent tutorial on VC-dimension and Support Vector Machines: C. J. C. Burges. A tutorial on support vector machines for pattern recognition. Data Mining and Knowledge Discovery, 2(2): 955 -974, 1998. http: //citeseer. nj. nec. com/burges 98 tutorial. html • The VC/SRM/SVM Bible: (Not for beginners including myself) Statistical Learning Theory by Vladimir Vapnik, Wiley. Interscience; 1998 • Software: SVM-light, http: //svmlight. joachims. org/, free download Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 75

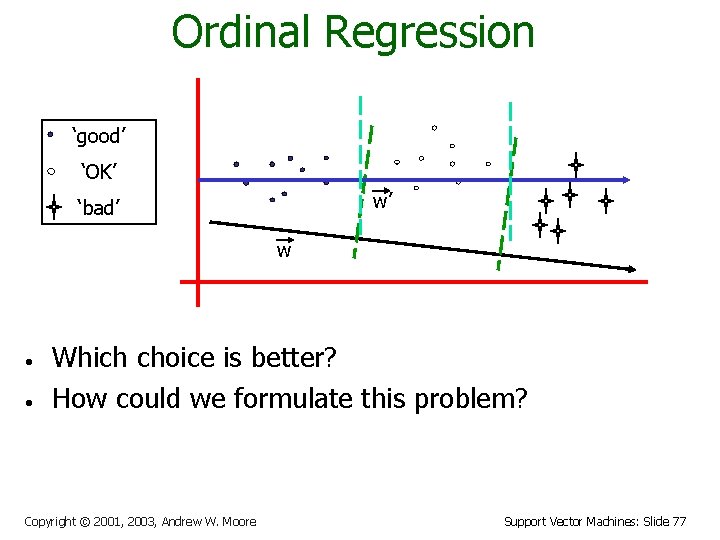
Ranking Problem • Consider a problem of ranking essays • Three ranking categories: good, ok, bad • Given a input document, predict its ranking category How should we formulate this problem? A simple multiple class solution • Each ranking category is a independent class But, there is something missing here … • We miss the ordinal relationship between classes ! • • • Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 76

Ordinal Regression ‘good’ ‘OK’ w’ ‘bad’ w • • Which choice is better? How could we formulate this problem? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 77

Ordinal Regression • What are the two decision boundaries? • What is the margin for ordinal regression? • Maximize margin Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 78

Ordinal Regression • What are the two decision boundaries? • What is the margin for ordinal regression? • Maximize margin Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 79

Ordinal Regression • What are the two decision boundaries? • What is the margin for ordinal regression? • Maximize margin Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 80

Ordinal Regression • How do we solve this monster ? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 81

Ordinal Regression • The same old trick To remove the scaling invariance, set • Now the problem is simplified as: • Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 82

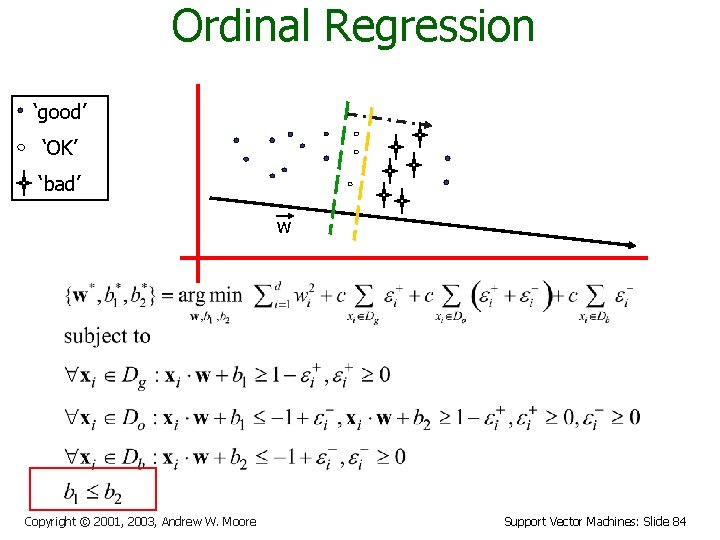
Ordinal Regression • Noisy case • Is this sufficient enough? Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 83

Ordinal Regression ‘good’ ‘OK’ ‘bad’ w Copyright © 2001, 2003, Andrew W. Moore Support Vector Machines: Slide 84