Special Relativity I Twin Paradox Added two Mastering

Special Relativity I “Twin Paradox” Added two Mastering Physics assignments Salvador Dali’s concept of time dilation Today: Quiz Special Relativity Read 37. 3 -37. 5 for next time 1

Q 8. 1 2

Q 8. 1 3

Q 8. 2 is the angular resolving power of an aperture, where λ is the wavelength and D is the aperture. A. This means that two objects with angular separation greater than this angle cannot be resolved by the aperture. B. This means that two objects with angular separation smaller than this angle cannot be resolved by the aperture. C. This means blobs with smaller wavelengths cannot be resolved. 4

Q 8. 2 is the angular resolving power of an aperture, where λ is the wavelength and D is the aperture. A. This means that two objects with angular separation greater than this angle cannot be resolved by the aperture. B. This means that two objects with angular separation smaller than this angle cannot be resolved by the aperture. C. This means blobs with smaller wavelengths cannot be resolved. 5

Q 8. 3 Which of the following postulates are in both Galilean theory of relativity and Einstein’s theory of relativity? A. All physical laws must be the same in all inertial reference frames. B. The speed of light in vacuum is the same in all inertial reference frames. C. Time intervals are the same in all inertial reference frames. D. Space intervals are the same in all inertial reference frames. 6

Q 8. 3 Which of the following postulates are in both Galilean theory of relativity and Einstein’s theory of relativity? A. All physical laws must be the same in all inertial reference frames. B. The speed of light in vacuum is the same in all inertial reference frames. C. Time intervals are the same in all inertial reference frames. D. Space intervals are the same in all inertial reference frames. 7

Q 8. 4 According to Einstein’s theory of relativity A. Two events that are simultaneous in one inertial frame must also be simultaneous in all inertial frames. B. Two events that are simultaneous in one inertial frame may not be simultaneous in all inertial frames. C. Events that are simultaneous in one inertial frame can never be simultaneous in another different inertial frame. 8

Q 8. 4 According to Einstein’s theory of relativity A. Two events that are simultaneous in one inertial frame must also be simultaneous in all inertial frames. B. Two events that are simultaneous in one inertial frame may not be simultaneous in all inertial frames. C. Events that are simultaneous in one inertial frame can never be simultaneous in another different inertial frame. 9

Wunderjahr Question: What was the “annus mirabilis” for Albert Einstein ? 1905: While working at the Swiss Patent office, he wrote four seminal papers that changed the course of history 1) Photoelectric effect 2) Brownian motion 3) Special relativity 4) Equivalence of mass and energy. 10

Goals for Chapter 37 • To understand the two postulates of relativity and their motivation • To see why two observers can disagree on simultaneity • To learn why moving clocks run slow • To see how motion affects length • To understand why velocity depends on the frame of reference • To calculate relativistic momentum and kinetic energy • To explore the key concepts of general relativity 11

Introduction • How do particles behave if they reach 99. 99% the speed of light? • What are the basic postulates behind special relativity? • Far-reaching and mind-blowing implications of relativity, such as the effect of motion on time Electrons (7 Ge. V) and (4 Ge. V) and length. The breakdown of positrons moving close to the speed of light around a 3. 0 km simultaneity. circumference tunnel at KEK in • Momentum and kinetic energy Tsukuba, Japan. must be redefined. The accelerator is “Super. KEKB” 12

Introduction – a warm up • What is the speed of light? A. 3 x 107 m/s B. 3 x 108 m/s C. 1. 5 x 107 m/s D. 3 x 109 m/s Electrons (7 Ge. V) and (4 Ge. V) positrons moving close to the speed of light around a 3. 1 km circumference tunnel at KEK in Tsukuba, Japan. The accelerator is “Super. KEKB” 13

Introduction – a warm up • What is the speed of light? A. 3 x 107 m/s B. 3 x 108 m/s C. 1. 5 x 107 m/s D. 3 x 109 m/s 187, 500 miles/s 675, 000 miles/hr Electrons (7 Ge. V) and (4 Ge. V) positrons moving close to the speed of light around a 3. 1 km circumference tunnel at KEK in Tsukuba, Japan. The accelerator is “Super. KEKB” 14

Introduction – a warm up • What is the speed of light? A. 3 x 107 m/s B. 3 x 108 m/s C. 1. 5 x 107 m/s D. 3 x 109 m/s • How long does it an electron/positron to orbit? A. 100 ns B. 1 μs C. 10 μs Electrons (7 Ge. V) and (4 Ge. V) positrons moving close to the speed of light around a 3. 1 km circumference tunnel at KEK in Tsukuba, Japan. The accelerator is “Super. KEKB” 15

Introduction – a warm up • What is the speed of light? A. 3 x 107 m/s B. 3 x 108 m/s C. 1. 5 x 107 m/s D. 3 x 109 m/s • How long does it an electron/positron to orbit? A. 100 ns B. 1 μs C. 10 μs • How many orbits/second? A. 100 billion B. 1 million C. 100 thousand Electrons (7 Ge. V) and (4 Ge. V) positrons moving close to the speed of light around a 3. 1 km circumference tunnel at KEK in Tsukuba, Japan. The accelerator is “Super. KEKB” 16

Introduction – a clicker warm up • What is the speed of light? A. 3 x 107 m/s B. 3 x 108 m/s C. 1. 5 x 107 m/s D. 3 x 109 m/s • How long does it an electron/positron to orbit? A. 100 ns B. 1 μs C. 10 μs • How many orbits/second? A. 100 billion B. 1 million C. 100 thousand Electrons (7 Ge. V) and (4 Ge. V) positrons moving close to the speed of light around a 3. 0 km circumference tunnel at KEK in Tsukuba, Japan. The accelerator is “Super. KEKB” 17

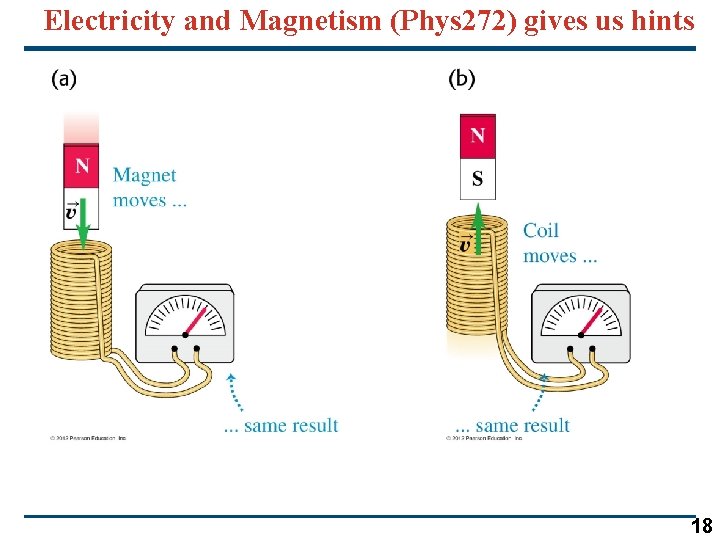
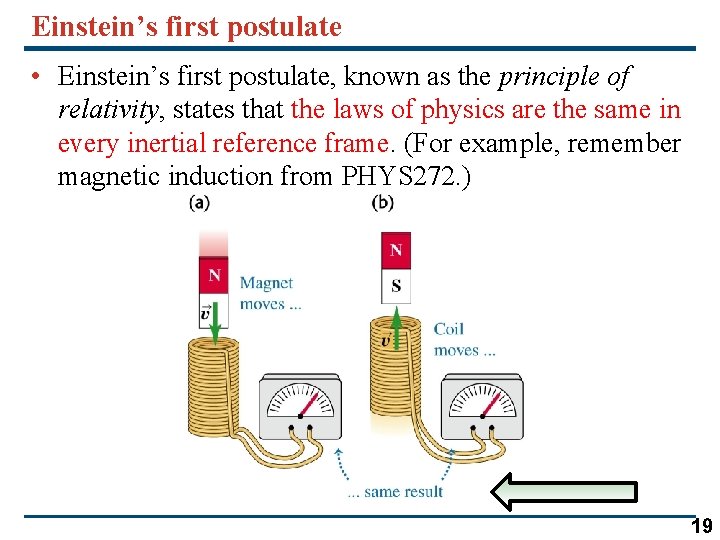
Electricity and Magnetism (Phys 272) gives us hints 18

Einstein’s first postulate • Einstein’s first postulate, known as the principle of relativity, states that the laws of physics are the same in every inertial reference frame. (For example, remember magnetic induction from PHYS 272. ) 19

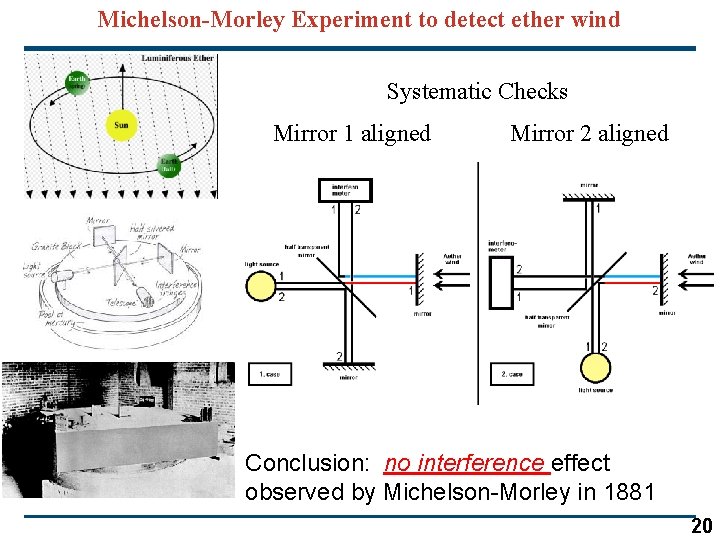
Michelson-Morley Experiment to detect ether wind Systematic Checks Mirror 1 aligned Mirror 2 aligned Conclusion: no interference effect observed by Michelson-Morley in 1881 20

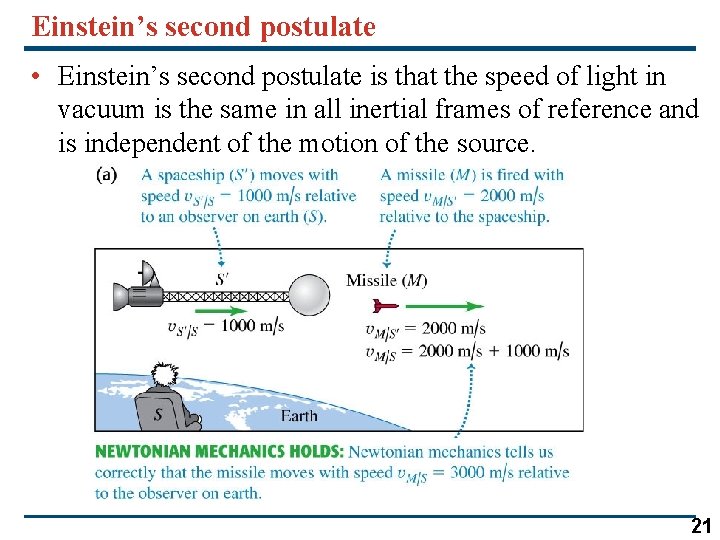
Einstein’s second postulate • Einstein’s second postulate is that the speed of light in vacuum is the same in all inertial frames of reference and is independent of the motion of the source. 21

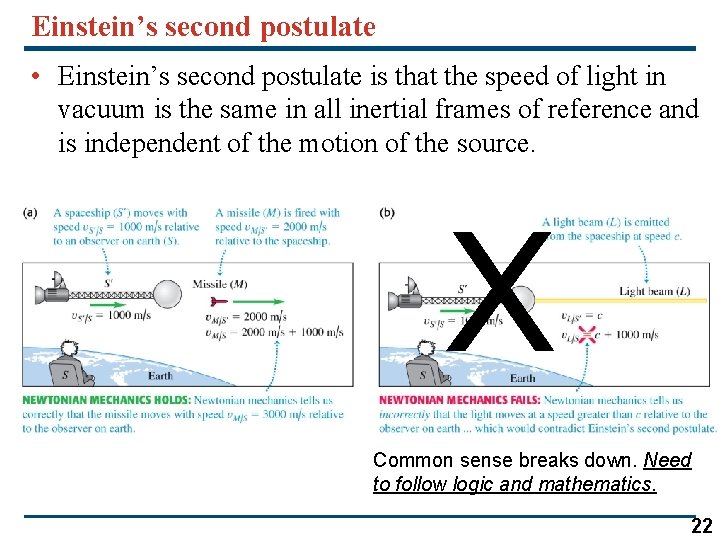
Einstein’s second postulate • Einstein’s second postulate is that the speed of light in vacuum is the same in all inertial frames of reference and is independent of the motion of the source. X Common sense breaks down. Need to follow logic and mathematics. 22

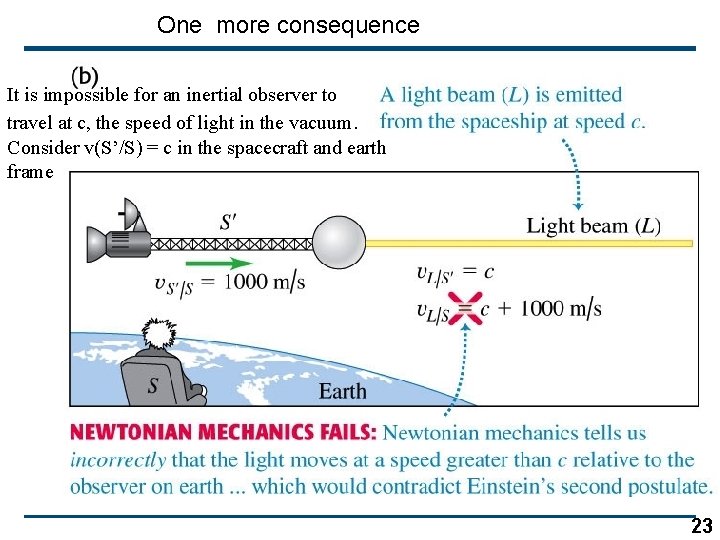
One more consequence It is impossible for an inertial observer to travel at c, the speed of light in the vacuum. Consider v(S’/S) = c in the spacecraft and earth frame 23

Einstein’s second postulate • Einstein’s second postulate is that the speed of light in vacuum is the same in all inertial frames of reference and is independent of the motion of the source. • As a consequence, it is impossible for an inertial observer to travel at c, the speed of light in the vacuum. 24

Galilean coordinate transformations have to be modified Review what are Galilean coordinate transformations ? (these work well at low relative velocities e. g. everyday life but not for GPS or particle accelerators) (x, y, z, t) are Earth coordinates; (x’, y’, z’, t’) are spacecraft coordinates. The spacecraft is moving at constant velocity u with respect to Earth. “obvious” 25

Galilean velocity transformations have to be modified (x, y, z, t) are Earth coordinates; (x’, y’, z’, t’) are spacecraft coordinates. The spacecraft is moving at velocity u with respect to Earth. Now differentiate with respect to time t “obvious” First worked this out in Chapter 3 of Young and Freedman ! But this does not work for u=c ! Violates Einstein’s second postulate 26

Galilean velocity transformations have to be modified But this does not work for u=c ! Violates Einstein’s second postulate. (speed of light is the same in all frames). Question: How can we fix this ? Something was wrong in the derivation. But what ? Ans: The assumption t=t’ is flawed. Need to introduce 4 dimensional spacetime (x, y, z, t) and (x’, y’, z’, t’) 27

Special Relativity Example • Example: As a high speed spaceship flies past you, it fires a strobe light that sends out a pulse of light in all directions. An observer aboard the spaceship measures a spherical wave front that speeds away from the spaceship at speed c in all directions. What do you measure ? A)Ellipsoidal with the long axis along the direction of the spaceship motion B) Spherical C) Ellipsoidal with the short axis along the direction of the spaceship’s motion D) not enough information given to decide 28

Special Relativity Example • Example: As a high speed spaceship flies past you, it fires a strobe light that sends out a pulse of light in all directions. An observer aboard the spaceship measures a spherical wave front that speeds away from the spaceship at speed c in all directions. What do you measure ? A)Ellipsoidal with the long axis along the direction of the spaceship motion B) Spherical C) Ellipsoidal with the short axis along the direction of the spaceship’s motion D) not enough information given to decide Ans: Spherical. the speed of light is the same in all reference frames ! Hence B) 29

Special Relativity Example (cont’d) • Example: As a high speed spaceship flies past you, it fires a strobe light that sends out a pulse of light in all directions. An observer aboard the spaceship measures a spherical wave front that speeds away from the spaceship at speed c in all directions. Is the spherical wavefront centered on the spaceship ? Ans: No. It is not centered on the current center of the spaceship but rather on the location of the spaceship where the light was emitted. Further explanation: If the spaceship is moving at c/3 and time t has elapsed since the pulse was emitted, the wavefront is a sphere of radius ct centered on P and the spaceship is now a distance of ct/3 away from P 30

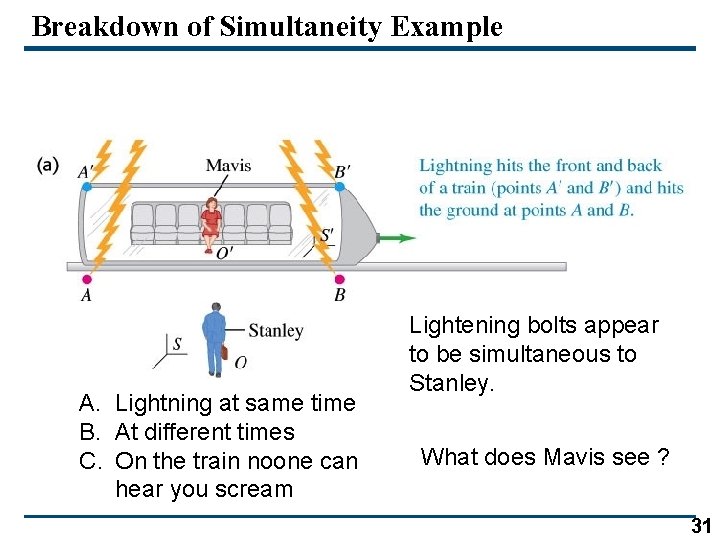
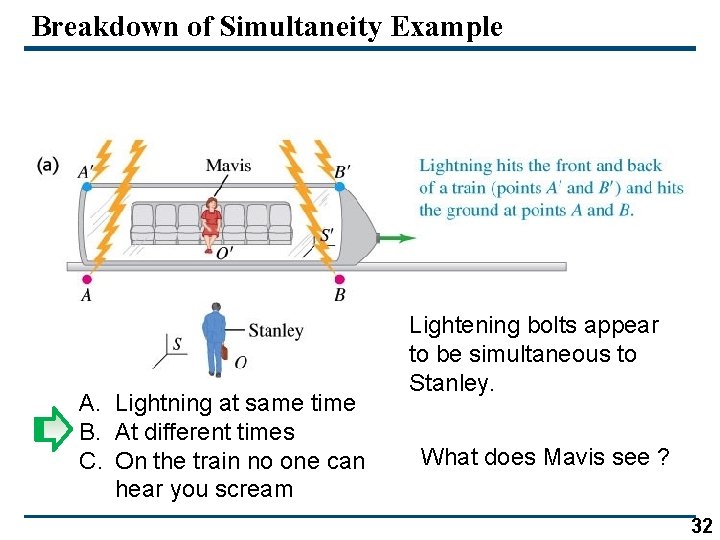
Breakdown of Simultaneity Example A. Lightning at same time B. At different times C. On the train noone can hear you scream Lightening bolts appear to be simultaneous to Stanley. What does Mavis see ? 31

Breakdown of Simultaneity Example A. Lightning at same time B. At different times C. On the train no one can hear you scream Lightening bolts appear to be simultaneous to Stanley. What does Mavis see ? 32