Some Comments on Root finding Some Comments on

Some Comments on Root finding

Some Comments on Root finding Consider the following two numbers 0. 123456789012345678 - 0. 123456789012345677 0. 0000000001 a= 0. 123456789012345678; b= 0. 123456789012345677; c=a-b ans = 0 Avoid subtraction of nearly equal numbers Associative property a=1 e-16; b=1; c=-1; a+(b+c) (a+b)+c ans = 1. 00000000 e-16 ans = 0 why

Some Comments on Root finding Avoid subtraction of nearly equal numbers Solve: rationalizing the numerator % solve x^2 + b*x + 1 = 0 f = @(x) x*(a*x+b)+c; xeps = 1 e-8; b = (2/xeps) + xeps; a=1; c=1; f = @(x) a*x^2 + b*x +c x 1 = (-b+sqrt(b^2 -4*a*c))/(2*a) y 1=(-2*c)/(b+sqrt(b^2 -4*a*c)) f(x 1) f(y 1) abs((x 1 -y 1)/y 1)*100 x 1 = 0 y 1 = -5. 00000000 e-09 ans = 100

Some Comments on Root finding Avoid subtraction of nearly equal numbers The Secant Method Algebraically equivalent formula in general, this iteration equation is likely to be less accurate than the one given in left box. Here, we subtract two nearly equal numbers in both numerator and denominator. why

Some Comments on Root finding Formula Error Equation guess x 0 suff close to x* Newton’s x 0 suff close to x* Secant Any Bisection Any Fixed-point False position Secant +test Any

Some Comments on Root finding Cq 1 solution Cq 2 solution

Some Comments on Root finding Newton’s method: 0 1 2 3 4 2. 00000 1. 3034338465 1. 3449403509 1. 3447510489 1. 3447510454 6. 9656615347 e-01 4. 1506504376 e-02 1. 8930200914 e-04 3. 5169049895 e-09

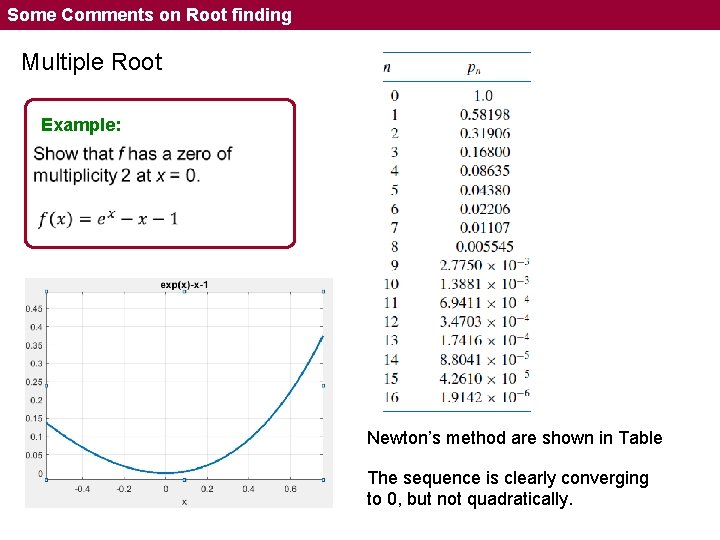
Some Comments on Root finding Multiple Root Note that no change of sign close to the root. (bisection , FP ? ? ) Definition: Theorem

Some Comments on Root finding Multiple Root Example: Newton’s method are shown in Table The sequence is clearly converging to 0, but not quadratically.

Some Comments on Root finding modification of Newton’s method If p is a zero of f of multiplicity m The only drawback to this method is the additional calculation of Example:

Some Comments on Root finding modification of Newton’s method If p is a zero of f of multiplicity m then p is also a fixed point of Example:

Some Comments on Root finding Nonlinear system of equations:

Some Comments on Root finding Def: Jacobian Matrix Example:

Some Comments on Root finding Newton’s method for single variable Newton’s method for system of nonlinear equations

Some Comments on Root finding Newton’s method for system of nonlinear equations This is a linear system of n -equations in n-unknowns

Some Comments on Root finding ALGORITHM: (Newton’s method for system of nonlinear equations) Given initial guess 1) Calculate Jacobian Matrix 2) Calculate right-hand-side vector 3) Solve the linear system: 4) update Repeat (1 - 4)

Some Comments on Root finding clear; clc f = @(x) [ x(1)^2+x(2)+… x(3)^2 -8; 2*x(1)+3*x(2)^2 -x(3)-11; x(1)^2+x(2)^2+x(3)^2 -14]; x=[1; -1; 1]; format short for n=1: 10 [J] = jacob(x); F = - f(x); y = JF x=x+y end x function [J] = jacob(x); J=[ 2*x(1) 1 2 6*x(2) 2*x(1) 2*x(2) 2*x(3); . . . -1 ; … 2*x(3)]; n 1 2 3 4 2. 0556 1. 1387 1. 0045 1. 0000 -2. 3333 -2. 0196 -2. 0001 -2. 0000 4. 1111 3. 2187 3. 0088 3. 0000