Solving Equations with Solving Equations 2 4 Variables

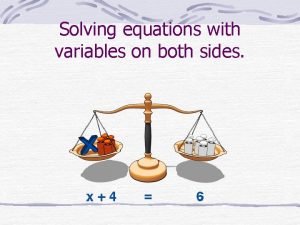
Solving Equations with Solving Equations 2 -4 Variables on Both Sides Warm Up Lesson Presentation Lesson Quiz Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Warm Up Simplify. 1. 4 x – 10 x – 6 x 2. – 7(x – 3) – 7 x + 21 3. 2 x + 3 4. 15 – (x – 2) 17 – x Solve. 5. 3 x + 2 = 8 2 6. Holt Algebra 1 28

Solving Equations with 2 -4 Variables on Both Sides Objective Solve equations in one variable that contain variable terms on both sides. Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Vocabulary identity contradiction Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides To solve an equation with variables on both sides, use inverse operations to "collect" variable terms on one side of the equation. Helpful Hint Equations are often easier to solve when the variable has a positive coefficient. Keep this in mind when deciding on which side to "collect" variable terms. Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Example 1: Solving Equations with Variables on Both Sides Solve 7 n – 2 = 5 n + 6 – 5 n 2 n – 2 = +2 2 n = To collect the variable terms on one side, subtract 5 n from both sides. 6 +2 8 Since n is multiplied by 2, divide both sides by 2 to undo the multiplication. n=4 Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Check It Out! Example 1 a Solve 4 b + 2 = 3 b – 3 b b+2= 0 – 2 b = – 2 Holt Algebra 1 To collect the variable terms on one side, subtract 3 b from both sides.

Solving Equations with 2 -4 Variables on Both Sides Check It Out! Example 1 b Solve 0. 5 + 0. 3 y = 0. 7 y – 0. 3 y 0. 5 +0. 3 0. 8 = 0. 4 y – 0. 3 + 0. 3 = 0. 4 y 2=y Holt Algebra 1 To collect the variable terms on one side, subtract 0. 3 y from both sides. Since 0. 3 is subtracted from 0. 4 y, add 0. 3 to both sides to undo the subtraction. Since y is multiplied by 0. 4, divide both sides by 0. 4 to undo the multiplication.

Solving Equations with 2 -4 Variables on Both Sides To solve more complicated equations, you may need to first simplify by using the Distributive Property or combining like terms. Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Example 2: Simplifying Each Side Before Solving Equations Solve 4 – 6 a + 4 a = – 1 – 5(7 – 2 a) Distribute – 5 to the expression in parentheses. 4 – 6 a + 4 a = – 1 – 5(7) – 5(– 2 a) 4 – 6 a + 4 a = – 1 – 35 + 10 a 4 – 2 a = – 36 + 10 a +36 40 – 2 a = + 2 a 40 = Holt Algebra 1 10 a +2 a 12 a Combine like terms. Since – 36 is added to 10 a, add 36 to both sides. To collect the variable terms on one side, add 2 a to both sides.

Solving Equations with 2 -4 Variables on Both Sides Example 2 Continued Solve 4 – 6 a + 4 a = – 1 – 5(7 – 2 a). 40 = 12 a Since a is multiplied by 12, divide both sides by 12. Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Check It Out! Example 2 a Solve . 1 Distribute to the expression in 2 parentheses. 3=b– 1 +1 +1 4=b Holt Algebra 1 To collect the variable terms on one side, subtract 1 b from 2 both sides. Since 1 is subtracted from b, add 1 to both sides.

Solving Equations with 2 -4 Variables on Both Sides Check It Out! Example 2 b Solve 3 x + 15 – 9 = 2(x + 2) Distribute 2 to the expression in parentheses. 3 x + 15 – 9 = 2(x) + 2(2) 3 x + 15 – 9 = 2 x + 4 3 x + 6 = 2 x + 4 – 2 x x+6= – 6 x = – 2 Holt Algebra 1 4 – 6 Combine like terms. To collect the variable terms on one side, subtract 2 x from both sides. Since 6 is added to x, subtract 6 from both sides to undo the addition.

Solving Equations with 2 -4 Variables on Both Sides An identity is an equation that is true for all values of the variable. An equation that is an identity has infinitely many solutions. A contradiction is an equation that is not true for any value of the variable. It has no solutions. Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Identities and Contradictions WORDS Identity When solving an equation, if you get an equation that is always true, the original equation is an identity, and it has infinitely many solutions. NUMBERS 2+1=2+1 3=3 ALGEBRA 2+x=2+x –x –x 2=2 Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Identities and Contradictions WORDS Contradiction When solving an equation, if you get a false equation, the original equation is a contradiction, and it has no solutions. NUMBERS 1=1+2 1=3 ALGEBRA x= x+3 –x –x 0=3 Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Example 3 A: Infinitely Many Solutions or No Solutions Solve 10 – 5 x + 1 = 7 x + 11 – 12 x Identify like terms. 11 – 5 x = 11 – 5 x + 5 x 11 = 11 Combine like terms on the left and the right. Add 5 x to both sides. True statement. The equation 10 – 5 x + 1 = 7 x + 11 – 12 x is an identity. All values of x will make the equation true. All real numbers are solutions. Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Example 3 B: Infinitely Many Solutions or No Solutions Solve 12 x – 3 + x = 5 x – 4 + 8 x Identify like terms. 13 x – 3 = 13 x – 4 – 13 x – 3 = – 4 Combine like terms on the left and the right. Subtract 13 x from both sides. False statement. The equation 12 x – 3 + x = 5 x – 4 + 8 x is a contradiction. There is no value of x that will make the equation true. There are no solutions. Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Check It Out! Example 3 a Solve 4 y + 7 – y = 10 + 3 y 3 y + 7 = 3 y + 10 – 3 y 7 = 10 Identify like terms. Combine like terms on the left and the right. Subtract 3 y from both sides. False statement. The equation 4 y + 7 – y = 10 + 3 y is a contradiction. There is no value of y that will make the equation true. There are no solutions. Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Check It Out! Example 3 b Solve 2 c + 7 + c = – 14 + 3 c + 21 Identify like terms. 3 c + 7 = 3 c + 7 Combine like terms on the left and the right. Subtract 3 c both sides. – 3 c 7= 7 True statement. The equation 2 c + 7 + c = – 14 + 3 c + 21 is an identity. All values of c will make the equation true. All real numbers are solutions. Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Example 4: Application Jon and Sara are planting tulip bulbs. Jon has planted 60 bulbs and is planting at a rate of 44 bulbs per hour. Sara has planted 96 bulbs and is planting at a rate of 32 bulbs per hour. In how many hours will Jon and Sara have planted the same number of bulbs? How many bulbs will that be? Person Bulbs Jon 60 bulbs plus 44 bulbs per hour Sara Holt Algebra 1 96 bulbs plus 32 bulbs per hour

Solving Equations with 2 -4 Variables on Both Sides Example 4: Application Continued Let b represent bulbs, and write expressions for the number of bulbs planted. When is 60 plus bulbs 60 + 44 bulbs each hour the same as 96 bulbs 44 b = 96 plus + 32 bulbs ? each hour 32 b 60 + 44 b = 96 + 32 b To collect the variable terms on one side, subtract 32 b – 32 b from both sides. 60 + 12 b = 96 Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Example 4: Application Continued 60 + 12 b = 96 – 60 12 b = 36 b=3 Holt Algebra 1 Since 60 is added to 12 b, subtract 60 from both sides. Since b is multiplied by 12, divide both sides by 12 to undo the multiplication.

Solving Equations with 2 -4 Variables on Both Sides Example 4: Application Continued After 3 hours, Jon and Sara will have planted the same number of bulbs. To find how many bulbs they will have planted in 3 hours, evaluate either expression for b = 3: 60 + 44 b = 60 + 44(3) = 60 + 132 = 192 96 + 32 b = 96 + 32(3) = 96 + 96 = 192 After 3 hours, Jon and Sara will each have planted 192 bulbs. Holt Algebra 1

Solving Equations with 2 -4 Variables on Both Sides Check It Out! Example 4 Four times Greg's age, decreased by 3 is equal to 3 times Greg's age increased by 7. How old is Greg? Let g represent Greg's age, and write expressions for his age. four times Greg's age 4 g Holt Algebra 1 decreased by 3 – 3 is equal to = three times Greg's age increased by 3 g + 7. 7

Solving Equations with 2 -4 Variables on Both Sides Check It Out! Example 4 Continued 4 g – 3 = 3 g + 7 – 3 g g– 3= +3 g= 7 +3 10 Greg is 10 years old. Holt Algebra 1 To collect the variable terms on one side, subtract 3 g from both sides. Since 3 is subtracted from g, add 3 to both sides.

Solving Equations with 2 -4 Variables on Both Sides Lesson Quiz Solve each equation. 1. 7 x + 2 = 5 x + 8 3 2. 4(2 x – 5) = 5 x + 4 8 3. 6 – 7(a + 1) = – 3(2 – a) 4. 4(3 x + 1) – 7 x = 6 + 5 x – 2 all real numbers 5. 1 6. A painting company charges $250 base plus $16 per hour. Another painting company charges $210 base plus $18 per hour. How long is a job for which the two companies costs are the same? 20 hours Holt Algebra 1