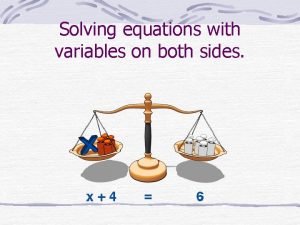
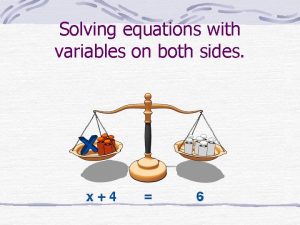
Solving Inequalities with Variables on on Both Sides

Solving Inequalities with Variables on on Both Sides Variables Both Sides Warm Up Lesson Presentation Lesson Quiz Holt 1 Algebra Mc. Dougal Holt. Algebra Mc. Dougal Algebra 11

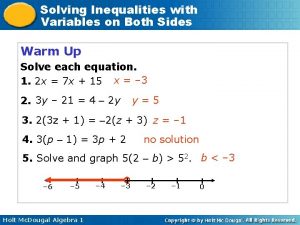
Solving Inequalities with Variables on Both Sides Warm Up Solve each equation. 1. 2 x = 7 x + 15 x = – 3 2. 3 y – 21 = 4 – 2 y y=5 3. 2(3 z + 1) = – 2(z + 3) z = – 1 4. 3(p – 1) = 3 p + 2 no solution 5. Solve and graph 5(2 – b) > 52. b < – 3 – 6 – 5 Holt Mc. Dougal Algebra 1 – 4 – 3 – 2 – 1 0

Solving Inequalities with Variables on Both Sides Objective Solve inequalities that contain variable terms on both sides. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Some inequalities have variable terms on both sides of the inequality symbol. You can solve these inequalities like you solved equations with variables on both sides. Use the properties of inequality to “collect” all the variable terms on one side and all the constant terms on the other side. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Example 1 A: Solving Inequalities with Variables on Both Sides Solve the inequality and graph the solutions. y ≤ 4 y + 18 To collect the variable terms on one y ≤ 4 y + 18 side, subtract y from both sides. –y –y 0 ≤ 3 y + 18 – 18 ≤ 3 y Since 18 is added to 3 y, subtract 18 from both sides to undo the addition. Since y is multiplied by 3, divide both sides by 3 to undo the multiplication. – 6 ≤ y (or y – 6) Holt Mc. Dougal Algebra 1 – 10 – 8 – 6 – 4 – 2 0 2 4 6 8 10

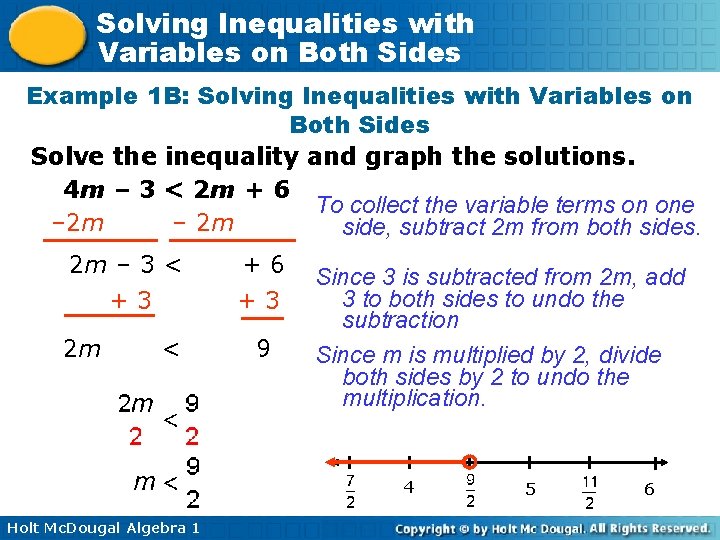
Solving Inequalities with Variables on Both Sides Example 1 B: Solving Inequalities with Variables on Both Sides Solve the inequality and graph the solutions. 4 m – 3 < 2 m + 6 To collect the variable terms on one – 2 m side, subtract 2 m from both sides. 2 m – 3 < +3 2 m < +6 +3 9 Since 3 is subtracted from 2 m, add 3 to both sides to undo the subtraction Since m is multiplied by 2, divide both sides by 2 to undo the multiplication. 4 Holt Mc. Dougal Algebra 1 5 6

Solving Inequalities with Variables on Both Sides Check It Out! Example 1 a Solve the inequality and graph the solutions. 4 x ≥ 7 x + 6 – 7 x To collect the variable terms on one side, subtract 7 x from both sides. – 3 x ≥ 6 x ≤ – 2 Since x is multiplied by – 3, divide both sides by – 3 to undo the multiplication. Change ≥ to ≤. – 10 – 8 – 6 – 4 – 2 Holt Mc. Dougal Algebra 1 0 2 4 6 8 10

Solving Inequalities with Variables on Both Sides Check It Out! Example 1 b Solve the inequality and graph the solutions. 5 t + 1 < – 2 t – 6 +2 t 7 t + 1 < – 6 – 1 < – 1 7 t < – 7 7 7 t < – 1 – 5 – 4 – 3 – 2 – 1 Holt Mc. Dougal Algebra 1 0 1 2 To collect the variable terms on one side, add 2 t to both sides. Since 1 is added to 7 t, subtract 1 from both sides to undo the addition. Since t is multiplied by 7, divide both sides by 7 to undo the multiplication. 3 4 5

Solving Inequalities with Variables on Both Sides Example 2: Business Application The Home Cleaning Company charges $312 to power-wash the siding of a house plus $12 for each window. Power Clean charges $36 per window, and the price includes power-washing the siding. How many windows must a house have to make the total cost from The Home Cleaning Company less expensive than Power Clean? Let w be the number of windows. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Example 2 Continued Home Cleaning Company siding charge 312 plus + $12 per window 12 times # of windows is less than Power Clean cost per window • w < 36 312 + 12 w < 36 w – 12 w 312 < 24 w times • # of windows. w To collect the variable terms, subtract 12 w from both sides. Since w is multiplied by 24, divide both sides by 24 to undo the multiplication. 13 < w The Home Cleaning Company is less expensive for houses with more than 13 windows. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Check It Out! Example 2 A-Plus Advertising charges a fee of $24 plus $0. 10 per flyer to print and deliver flyers. Print and More charges $0. 25 per flyer. For how many flyers is the cost at A-Plus Advertising less than the cost of Print and More? Let f represent the number of flyers printed. A-Plus Advertising plus fee of $24 24 + $0. 10 per flyer times # of flyers 0. 10 • f Holt Mc. Dougal Algebra 1 is less than < Print and More’s cost per flyer 0. 25 times • # of flyers. f

Solving Inequalities with Variables on Both Sides Check It Out! Example 2 Continued 24 + 0. 10 f < 0. 25 f – 0. 10 f 24 To collect the variable terms, subtract 0. 10 f from both sides. < 0. 15 f Since f is multiplied by 0. 15, divide both sides by 0. 15 to undo the multiplication. 160 < f More than 160 flyers must be delivered to make A-Plus Advertising the lower cost company. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides You may need to simplify one or both sides of an inequality before solving it. Look for like terms to combine and places to use the Distributive Property. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Example 3 A: Simplify Each Side Before Solving Solve the inequality and graph the solutions. 2(k – 3) > 6 + 3 k – 3 Distribute 2 on the left side of 2(k – 3) > 3 + 3 k the inequality. 2 k + 2(– 3) > 3 + 3 k 2 k – 6 > 3 + 3 k – 2 k – 6 > 3 + k – 3 – 9 > k Holt Mc. Dougal Algebra 1 To collect the variable terms, subtract 2 k from both sides. Since 3 is added to k, subtract 3 from both sides to undo the addition.

Solving Inequalities with Variables on Both Sides Example 3 A Continued – 9 > k – 12 – 9 Holt Mc. Dougal Algebra 1 – 6 – 3 0 3

Solving Inequalities with Variables on Both Sides Example 3 B: Simplify Each Side Before Solving Solve the inequality and graph the solution. 0. 9 y ≥ 0. 4 y – 0. 5 – 0. 4 y To collect the variable terms, subtract 0. 4 y from both sides. 0. 5 y ≥ – 0. 5 y ≥ – 1 – 5 – 4 – 3 – 2 – 1 Holt Mc. Dougal Algebra 1 0 1 2 3 Since y is multiplied by 0. 5, divide both sides by 0. 5 to undo the multiplication. 4 5

Solving Inequalities with Variables on Both Sides Check It Out! Example 3 a Solve the inequality and graph the solutions. 5(2 – r) ≥ 3(r – 2) Distribute 5 on the left side of the inequality and distribute 3 on 5(2 – r) ≥ 3(r – 2) the right side of the inequality. 5(2) – 5(r) ≥ 3(r) + 3(– 2) Since 6 is subtracted from 3 r, 10 – 5 r ≥ 3 r – 6 add 6 to both sides to undo +6 +6 the subtraction. 16 − 5 r ≥ 3 r Since 5 r is subtracted from 16 + 5 r +5 r add 5 r to both sides to undo 16 ≥ 8 r Holt Mc. Dougal Algebra 1 the subtraction.

Solving Inequalities with Variables on Both Sides Check It Out! Example 3 a Continued 16 ≥ 8 r Since r is multiplied by 8, divide both sides by 8 to undo the multiplication. 2≥r – 6 – 4 Holt Mc. Dougal Algebra 1 – 2 0 2 4

Solving Inequalities with Variables on Both Sides Check It Out! Example 3 b Solve the inequality and graph the solutions. 0. 5 x – 0. 3 + 1. 9 x < 0. 3 x + 6 2. 4 x – 0. 3 < 0. 3 x + 6 Simplify. Since 0. 3 is subtracted 2. 4 x – 0. 3 < 0. 3 x + 6 from 2. 4 x, add 0. 3 to + 0. 3 both sides. 2. 4 x < 0. 3 x + 6. 3 Since 0. 3 x is added to – 0. 3 x 6. 3, subtract 0. 3 x from both sides. 2. 1 x < 6. 3 Since x is multiplied by 2. 1, divide both sides by 2. 1. x<3 Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Check It Out! Example 3 b Continued x<3 – 5 – 4 – 3 – 2 – 1 Holt Mc. Dougal Algebra 1 0 1 2 3 4 5

Solving Inequalities with Variables on Both Sides Some inequalities are true no matter what value is substituted for the variable. For these inequalities, all real numbers are solutions. Some inequalities are false no matter what value is substituted for the variable. These inequalities have no solutions. If both sides of an inequality are fully simplified and the same variable term appears on both sides, then the inequality has all real numbers as solutions or it has no solutions. Look at the other terms in the inequality to decide which is the case. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Additional Example 4 A: All Real Numbers as Solutions or No Solutions Solve the inequality. 2 x – 7 ≤ 5 + 2 x The same variable term (2 x) appears on both sides. Look at the other terms. For any number 2 x, subtracting 7 will always result in a lower number than adding 5. All values of x make the inequality true. All real numbers are solutions. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Additional Example 4 B: All Real Numbers as Solutions or No Solutions Solve the inequality. 2(3 y – 2) – 4 ≥ 3(2 y + 7) 6 y – 8 ≥ 6 y + 21 Distribute 2 on the left side and 3 on the right side and combine like terms. The same variable term (6 y) appears on both sides. Look at the other terms. For any number 6 y, subtracting 8 will never result in a higher number than adding 21. No values of y make the inequality true. There are no solutions. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Check It Out! Example 4 a Solve the inequality. 4(y – 1) ≥ 4 y + 2 4 y – 4 ≥ 4 y + 2 Distribute 4 on the left side. The same variable term (4 y) appears on both sides. Look at the other terms. For any number 4 y, subtracting 4 will never result in a higher number than adding 2. No values of y make the inequality true. There are no solutions. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Check It Out! Example 4 b Solve the inequality. x– 2<x+1 The same variable term (x) appears on both sides. Look at the other terms. For any number x, subtracting 2 will always result in a lesser number than adding 1. All values of x make the inequality true. All real numbers are solutions. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Lesson Quiz: Part I Solve each inequality and graph the solutions. 1. t < 5 t + 24 t > – 6 2. 5 x – 9 ≤ 4. 1 x – 81 x ≤ – 80 3. 4 b + 4(1 – b) > b – 9 Holt Mc. Dougal Algebra 1 b < 13

Solving Inequalities with Variables on Both Sides Lesson Quiz: Part I Solve each inequality and graph the solutions. 1. t < 5 t + 24 t > – 6 2. 5 x – 9 ≤ 4. 1 x – 81 x ≤ – 80 3. 4 b + 4(1 – b) > b – 9 b < 13 4. 2 y – 2 ≥ 2(y + 7) 5. 2(– 6 r – 5) < – 3(4 r + 2) Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Lesson Quiz: Part II 4. Rick bought a photo printer and supplies for $186. 90, which will allow him to print photos for $0. 29 each. A photo store charges $0. 55 to print each photo. How many photos must Rick print before his total cost is less than getting prints made at the photo store? Rick must print more than 718 photos. Holt Mc. Dougal Algebra 1

Solving Inequalities with Variables on Both Sides Lesson Quiz: Part III Solve each inequality. 5. 2 y – 2 ≥ 2(y + 7) no solutions 6. 2(– 6 r – 5) < – 3(4 r + 2) all real numbers Holt Mc. Dougal Algebra 1