Solving equations with variables on both sides Learning

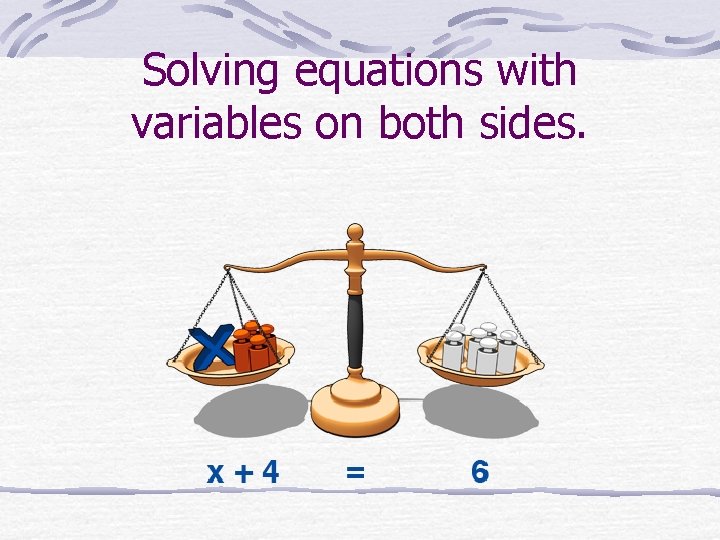
Solving equations with variables on both sides.

Learning Goal for Focus 2 (HS. A-CED. A. 1, 2 & 3, HS. A-REI. A. 1, HS. A-REI. B. 3): The student will create equations from multiple representations and solve linear equations and inequalities in one variable explaining the logic in each step. 4 3 2 1 0 In addition to level 3. 0 and above and beyond what was taught in class, the student may: - Make connection with other concepts in math - Make connection with other content areas. The student will create equations from multiple representations and solve linear equations and inequalities in one variable explaining the logic in each step. - rearrange formulas to highlight a quantity of interest. -Graph created equations on a coordinate graph. The student will be able to solve linear equations and inequalities in one variable and explain the logic in each step. -Use equations and inequalities in one variable to solve problems. With help from the teacher, the student has partial success with solving linear equations and inequalities in one variable. Even with help, the student has no success with solving linear equations and inequalities in one variable.

When you have variables on both sides, move them to one side. Usually we move the variable to the left side, but if it makes the variable negative, you might want to move it to the right side to keep it positive. Your answer must have a variable positive! Either way you will get the same answer.

Solve both ways: 9 x – 8 = 4 x + 12 -4 x 5 x – 8 = 12 +8 + 8 5 x = 20 5 5 x=4 9 x – 8 = 4 x + 12 -9 x – 8 = -5 x + 12 -20 = -5 x -5 -5 4=x

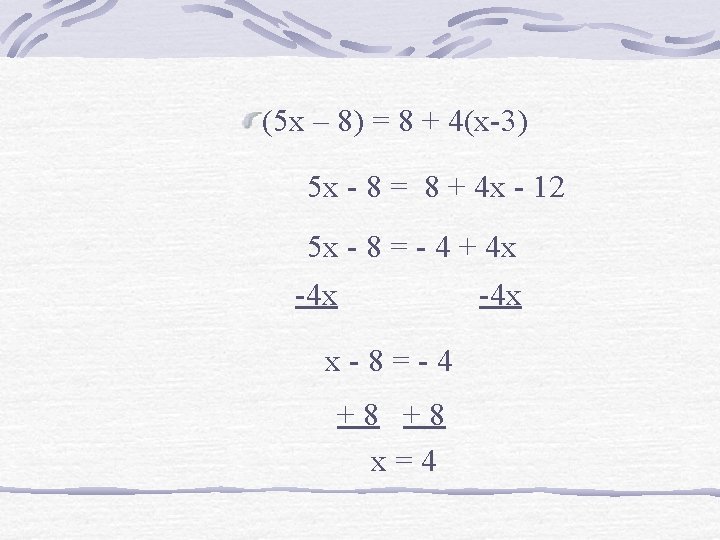
(5 x – 8) = 8 + 4(x-3) 5 x - 8 = 8 + 4 x - 12 5 x - 8 = - 4 + 4 x -4 x x-8=-4 +8 +8 x=4

When will I ever use this? ? ? You want to rent video games and can’t decide which store to rent from. Store 1 charges $8 per game for 3 days and no membership fee. Store 2 charges a $50 membership fee, plus $3 per game for 3 days. Which store is a better choice?

Set up an equation to solve. Hint: set both stores equal to each other. This will give you the break even point. Write a verbal model. Label the unknown. Write the equation. Solve Answer the question.

Solution: Store 1 rental fee #rentals=Store 2 membership fee+rental fee #rentals. Let x = number of games rented. 8 x=50+3 x 5 x=50 x=10 After 10 rentals Store 2 would be a better choice.