Solving Equations with Variables on Both Sides Essential

Solving Equations with Variables on Both Sides Essential Question? How can you represent and solve equations with variables on both sides? 8. EE. 7

Common Core Standard: 8. EE. 7 ─ Analyze and solve linear equations and pairs of simultaneous linear equations. Solve linear equations in one variable. b. Solve linear equations with rational number coefficients, including equations whose solutions require expanding expressions using the distributive property and collecting like terms.

Objectives: • To represent and solve equations with variables on both sides.

Curriculum Vocabulary Algebraic Expression (expresión algebraica): An expression that contains at least one variable. Constant (constante): A value that does not change. Equation (ecuación): A mathematical sentence that shows that two expressions are equivalent. Coefficient (coeficiente): The number that is multiplied by the variable in an algebraic expression.

Curriculum Vocabulary Operations (operaciones): Mathematical procedures including, but not limited to; addition, subtraction, multiplication and division. Solution (solución): A value or values that make a statement true. Variable (variable): A symbol used to represent a quantity that can change. Least Common Multiple (mínimo común múltiplo): The smallest whole number, other than zero, that is a multiple of two or more given numbers.

The SIX STEPS to Solving Equations 1) Look for the DISTRIBUTIVE PROPERTY Distribute if necessary 2) Look to COMBINE LIKE TERMS on the same sides of the equation Combine Like Terms if necessary 3) Move the variable for which you are solving to the same side of the equation Use OPPOSITES!

The SIX STEPS to Solving Equations 4) Undo the WEAK LINKS ADDITION & SUBTRACTION Use OPPOSITES! 5) Undo the STRONG LINKS MULTIPLICATION & DIVISION Multiply by reciprocal! 6) CHECK Use SUBSTITUTION

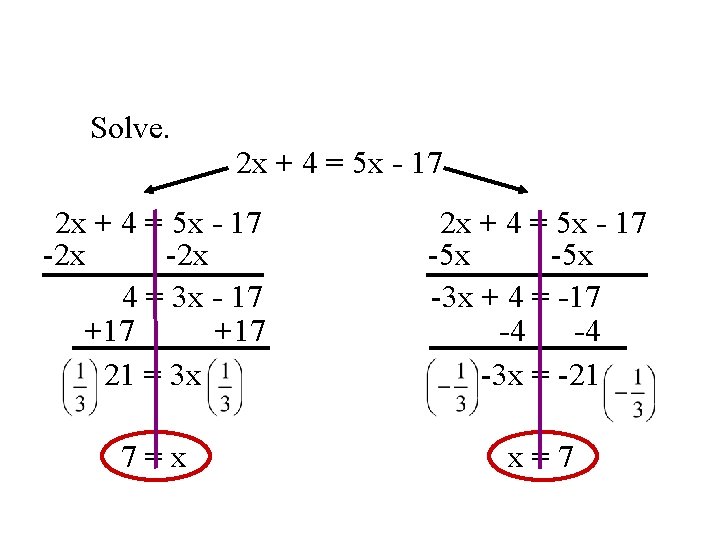
Solve. 2 x + 4 = 5 x - 17 -2 x 4 = 3 x - 17 +17 21 = 3 x 2 x + 4 = 5 x - 17 -5 x -3 x + 4 = -17 -4 -4 -3 x = -21 7=x x=7

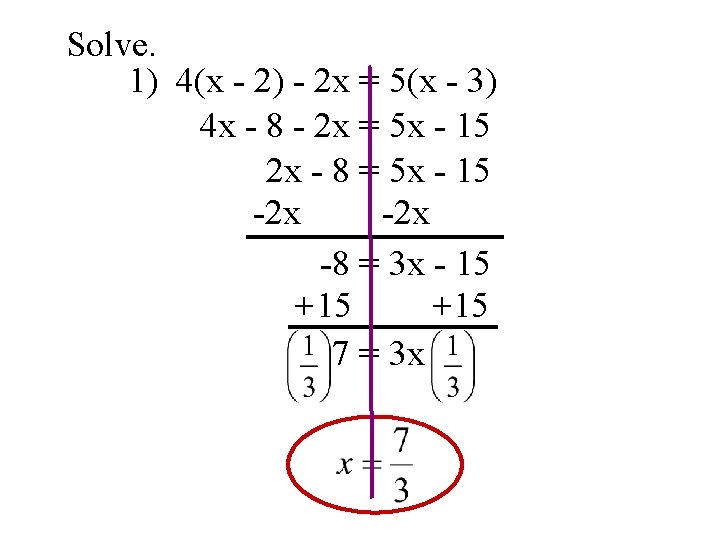
Solve. 1) 4(x - 2) - 2 x = 5(x - 3) 4 x - 8 - 2 x = 5 x - 15 2 x - 8 = 5 x - 15 -2 x -8 = 3 x - 15 +15 7 = 3 x

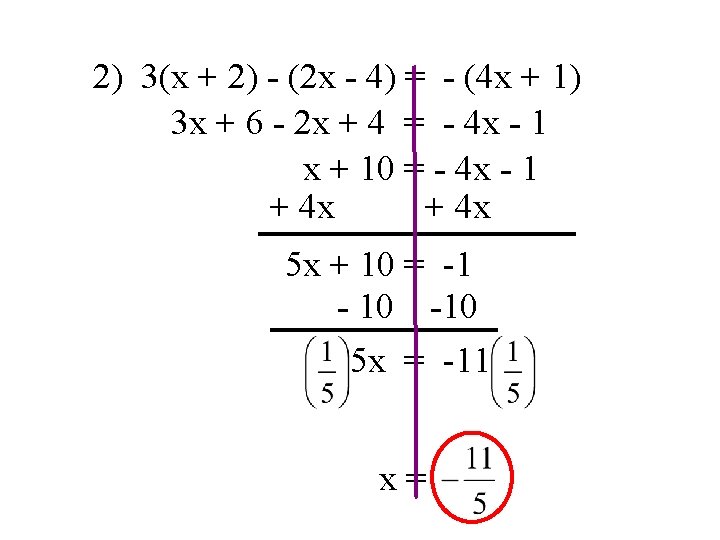
2) 3(x + 2) - (2 x - 4) = - (4 x + 1) 3 x + 6 - 2 x + 4 = - 4 x - 1 x + 10 = - 4 x - 1 + 4 x 5 x + 10 = -1 - 10 -10 5 x = -11 x=

3) 5(m - 6) = 10 - 4[2(m - 7) - 5 m] 5 m - 30 = 10 - 4[2 m - 14 - 5 m] 5 m - 30 = 10 - 4[-3 m - 14] 5 m - 30 = 10 + 12 m + 56 5 m - 30 = 12 m + 66 -5 m -30 = 7 m + 66 -66 -96 = 7 m

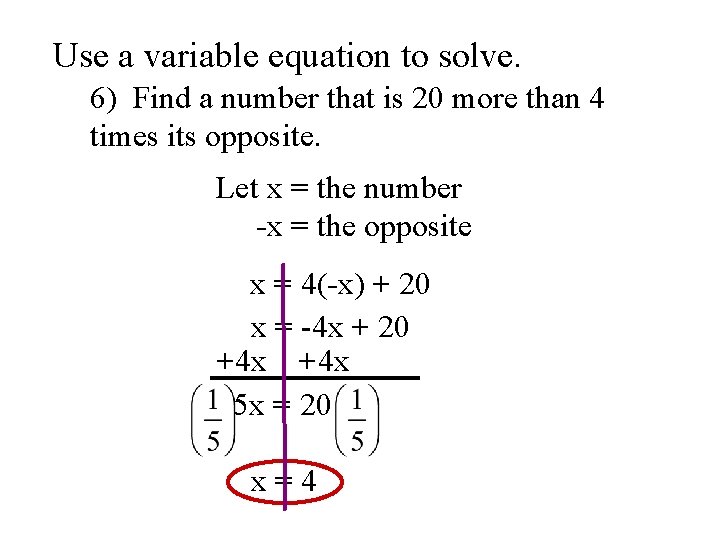
Use a variable equation to solve. 6) Find a number that is 20 more than 4 times its opposite. Let x = the number -x = the opposite x = 4(-x) + 20 x = -4 x + 20 +4 x 5 x = 20 x=4