Solving and Graphing Inequalities in Two Variables Todays

Solving and Graphing Inequalities in Two Variables

Today’s Learning Goal n n We will be able to graph inequalities in two variables. We will be able to determine solutions for inequalities in two variables.

Review n n x > 3½ Previously, we discussed how solutions to inequalities can be graphed on a number line. To review, how would we show all of the values that satisfy the inequality above using the number line: -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 n n Is x = -1 a solution to the above inequality? No…it is not a part of the shaded region. Is x = 3½ a solution to the inequality? No…it is not a part of the shaded region. x

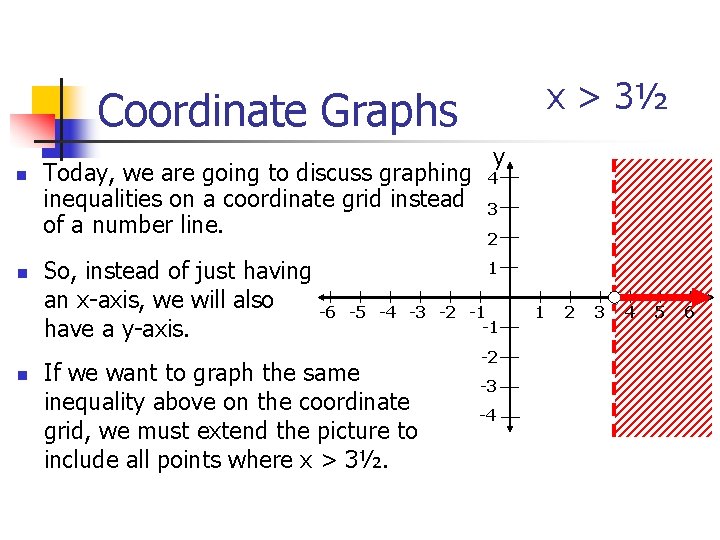
x > 3½ Coordinate Graphs n n n Today, we are going to discuss graphing inequalities on a coordinate grid instead of a number line. So, instead of just having an x-axis, we will also -6 have a y-axis. y 4 3 2 1 -5 -4 -3 -2 -1 -1 If we want to graph the same inequality above on the coordinate grid, we must extend the picture to include all points where x > 3½. -2 -3 -4 1 2 3 4 5 6

x > 3½ Coordinate Graphs n n Consider the green point. Does it satisfy the inequality above? 4 Yes…because it’s x-value is > 3½. 2 Does the blue point satisfy the inequality? (3½, 3½ 4) 3 (4, 4 1) 1 -6 -5 -4 -3 -2 -1 -1 No…because it’s x-value is NOT > 3½. n y Does the yellow point satisfy the inequality? No…because it’s x-value is NOT > 3½. -2 -3 -4 1 2 (1, 1 -3) 3 4 5 6

x > 3½ Coordinate Graphs n Which region contains all of the points that satisfy the above inequality? Awesome…any point in the red region has an x-value > 3½. n n How many solutions are -6 -5 there for this inequality? Fantastic…there an infinite number of solutions! y 4 3 2 1 -4 -3 -2 -1 -1 Again, a solution to an inequality is a point that is in the shaded region! -2 -3 -4 1 2 3 4 5 6

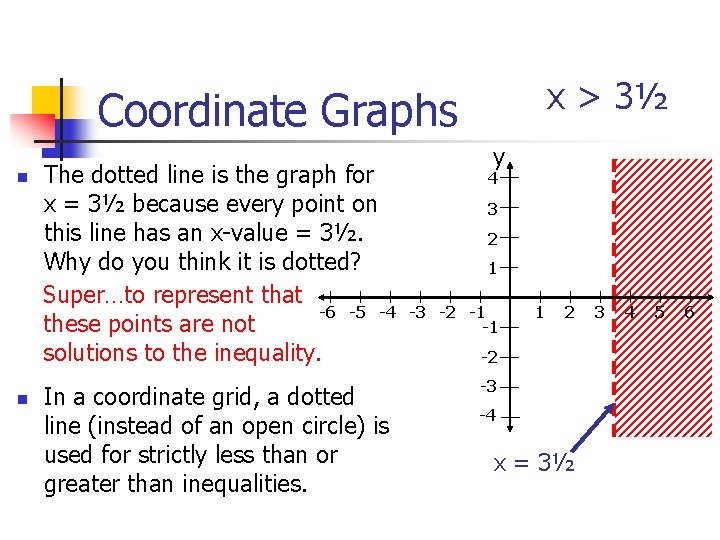
x > 3½ Coordinate Graphs n n The dotted line is the graph for x = 3½ because every point on this line has an x-value = 3½. Why do you think it is dotted? Super…to represent that -6 -5 -4 these points are not solutions to the inequality. In a coordinate grid, a dotted line (instead of an open circle) is used for strictly less than or greater than inequalities. y 4 3 2 1 -3 -2 -1 -1 1 2 -2 -3 -4 x = 3½ 3 4 5 6

X-inequalities n n n x -2 Consider the inequality above. Other than the number, what is different about this inequality compared to the last one we discussed? Nice…it is less than or equal to! Will points that have a value of x = -2 be included as solutions for this inequality? Yes…because it is less than or equal to (not strictly less than)! For inequalities that include the boundary value, we use solid lines (instead of solid circles) to indicate that those points are solutions to the inequality.

x -2 Coordinate Graphs n n n How would you graph the inequality above? Is the green point a solution to the inequality? Yes…because it’s x-value -6 is equal to -2. Is the yellow point a solution to the inequality? No…because it’s x-value is NOT -2. y (-2, -2 3) 4 3 2 1 -5 -4 -3 -2 -1 -1 -2 1 2 (0, 0 -2) -3 -4 x = -2 3 4 5 6

X-inequalities n n y > -3. 2 Unfortunately, the TI-84 graphing calculators do not graph x-inequalities. You need to know how to do them by hand. However, y-inequalities like the one above can be graphed using the graphing calculator.

y > -3. 2 Graphing Calculator n n n Go to your Y= screen. Type in y = -3. 2 as if it was a regular equation. Cursor to the left of Y 1 = to put the cursor over top of the diagonal line. While the cursor is to the left, keep pressing Enter until you see a triangle pointing up and to the right like shown. The triangle pointing up means greater than or equal to!

y > -3. 2 Graphing Calculator n n Go to your window and make it match the one to the right. Now press “Graph” to see the graph of the inequality. Notice that the graphing calculator put a solid line for the inequality above. Is this correct? No…because the inequality is strictly greater than! Unfortunately, graphing calculators don’t show dotted lines. You have to remember that!

y > -3. 2 Graphing Calculator n n What is the equation of the line separating the shaded and unshaded regions? Is (-3. 2, 5) a solution to the inequality? Yes…because it is in the shaded region and the y-value > -3. 2! n Is (2, -3. 2) a solution to the inequality? No…because the y-value is NOT > -3. 2! y=-3. 2

Inequalities in Two Variables n n n x – 2 y -8 Consider the inequality above. What would we need to do to make a graph of this using our graphing calculator? x – 2 y -8 -x -x Excellent…put it into y = mx + b form. -2 y -8 – x What would you do first? Perfect…subtract x from both sides. What is the resulting inequality?

Inequalities in Two Variables n n n x – 2 y -8 What is the last step? Great…divide both sides by -2. x – 2 y -8 -x -x -2 y -8 – x -2 -2 -2 What is the resulting inequality? y 4 + ½x Don’t forget that when you multiply or divide both sides by a negative amount, you need to switch the sign of the inequality (because you are taking the opposite of everything)!

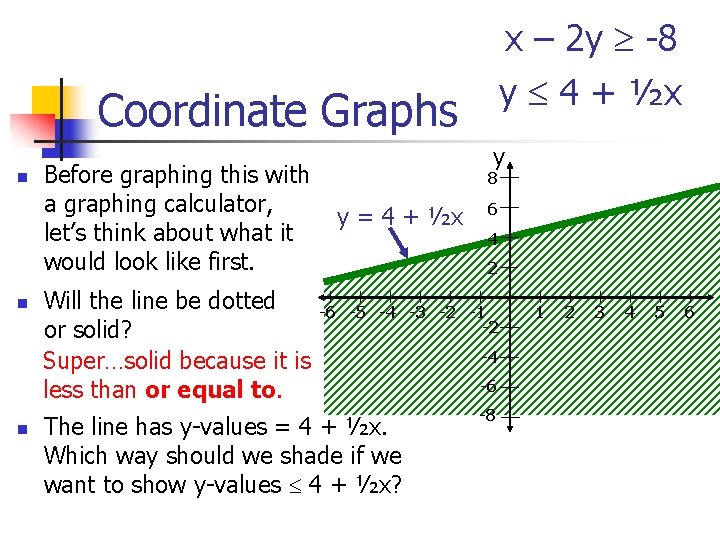
x – 2 y -8 y 4 + ½x Coordinate Graphs n n n Before graphing this with a graphing calculator, let’s think about what it would look like first. Will the line be dotted or solid? Super…solid because it is less than or equal to. y 8 y = 4 + ½x 6 4 2 -6 -5 -4 -3 -2 -1 -2 The line has y-values = 4 + ½x. Which way should we shade if we want to show y-values 4 + ½x? -4 -6 -8 1 2 3 4 5 6

y 4 + ½x Graphing Calculator n n n Let’s graph this inequality on our graphing calculator. Cursor to the left of Y 1 = to put the cursor over top of the diagonal line. Because we want , push Enter until you see a triangle pointing down and to the left to represent .

y 4 + ½x Graphing Calculator n n n Go to your window and make it match the one to the right. Now press “Graph” to see the graph of the inequality. Notice that the graphing calculator put a solid line for the inequality above. Is this correct? Yes…because the inequality is less than or equal to!

y 4 + ½x Graphing Calculator n n y=4+½x What is the equation of the line separating the shaded and unshaded regions? Is (-2, 3) a solution to the inequality? Yes…because this point is on the line: y = 4 + ½(-2) = 3! Is (2, 8) a solution to the inequality? No…because on the line at x = 2, y = 4 + ½(2) = 5 and 8 is above 5! n

y 4 + ½x Graphing Calculator n n n To determine if (2, 8) is a solution to the inequality above, we plug x = 2 into the equation: y = 4 + ½x(2) =4+1 =5 So, now we know that (2, 5) is a point on the line. Therefore, (2, 8) would be above the line and not in the shaded region. Thus, (2, 8) is not a solution to the inequality. y=4+½x

Partner Work n You have 20 minutes to work on the following questions with your partner.

For those that finish early What is wrong with each of the following graphs for 4 x – 2 y < 6? a) b) n y = -3 – 2 x c) y = -3 – 2 x d) y = -3 + 2 x

Big Ideas from Today’s Lesson n Dotted lines are used to represent strictly less than or greater than inequalities. Solid lines are used to represent or inequalities. The solutions to the inequality are within the shaded region.

Homework n n Complete the homeworksheet. Pgs. 355 – 357 (1, 6, 7 – 17 odds, 20 – 25, 47, 48)