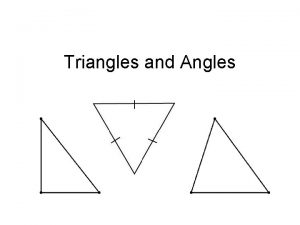
4 1 Classifying Triangles Warm Up Lesson Presentation

4 -1 Classifying. Triangles Warm Up Lesson Presentation Lesson Quiz Holt Geometry

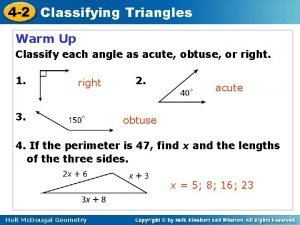
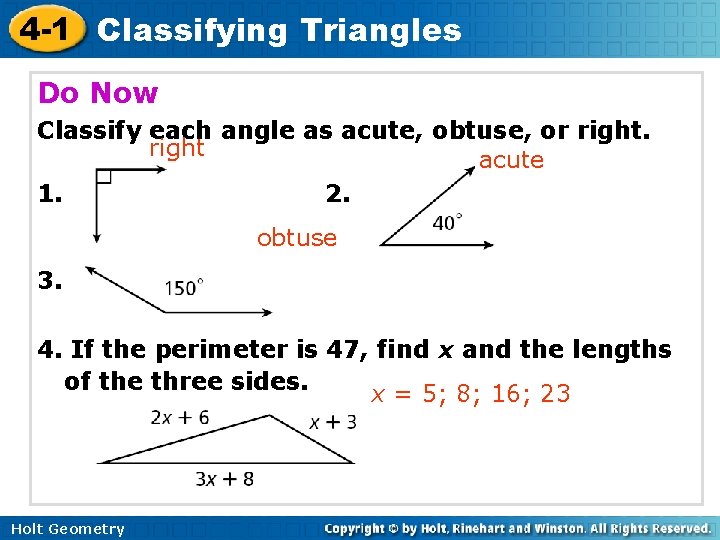
4 -1 Classifying Triangles Do Now Classify each angle as acute, obtuse, or right acute 1. 2. obtuse 3. 4. If the perimeter is 47, find x and the lengths of the three sides. x = 5; 8; 16; 23 Holt Geometry

4 -1 Classifying Triangles Objectives Classify triangles by their angle measures and side lengths. Use triangle classification to find angle measures and side lengths. Holt Geometry

4 -1 Classifying Triangles Vocabulary acute triangle equiangular triangle right triangle obtuse triangle equilateral triangle isosceles triangle scalene triangle Holt Geometry

4 -1 Classifying Triangles Recall that a triangle ( ) is a polygon with three sides. Triangles can be classified in two ways: by their angle measures or by their side lengths. Holt Geometry

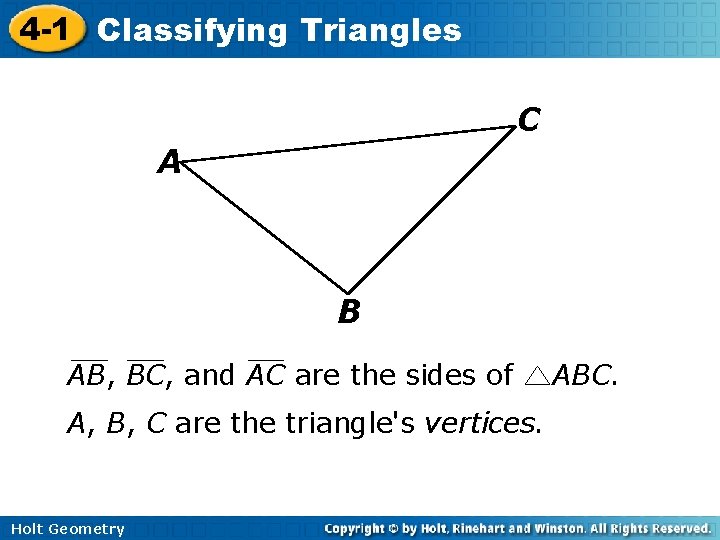
4 -1 Classifying Triangles C A B AB, BC, and AC are the sides of A, B, C are the triangle's vertices. Holt Geometry ABC.

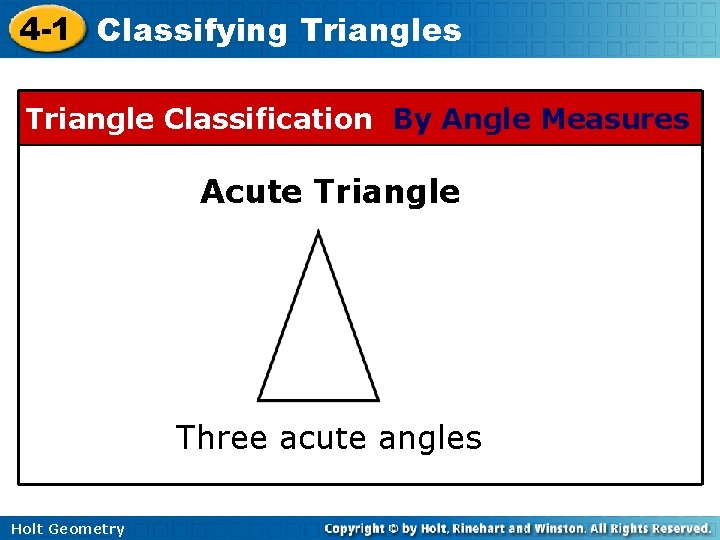
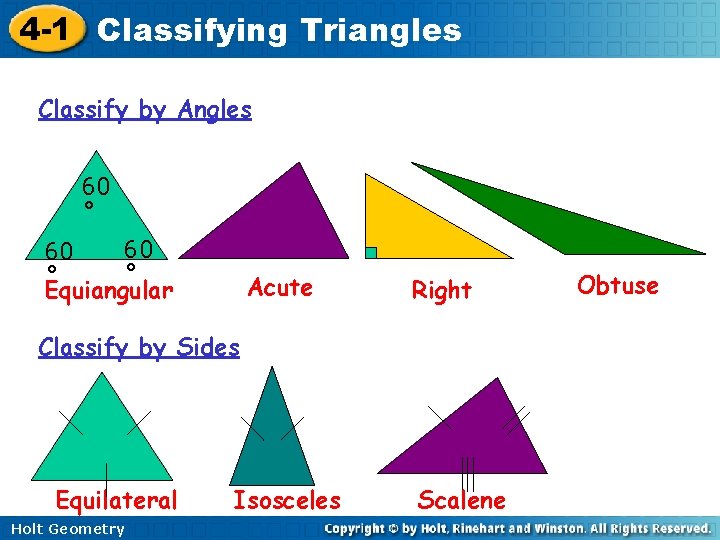
4 -1 Classifying Triangles Triangle Classification By Angle Measures Acute Triangle Three acute angles Holt Geometry

4 -1 Classifying Triangles Triangle Classification By Angle Measures Equiangular Triangle Three congruent acute angles Holt Geometry

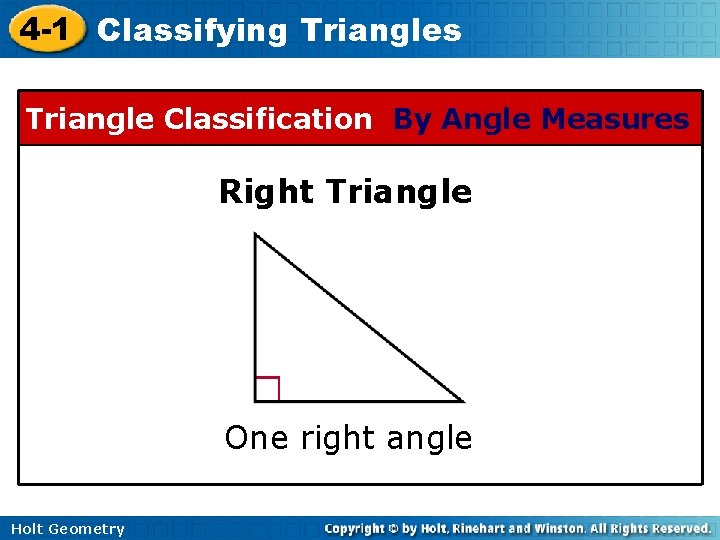
4 -1 Classifying Triangles Triangle Classification By Angle Measures Right Triangle One right angle Holt Geometry

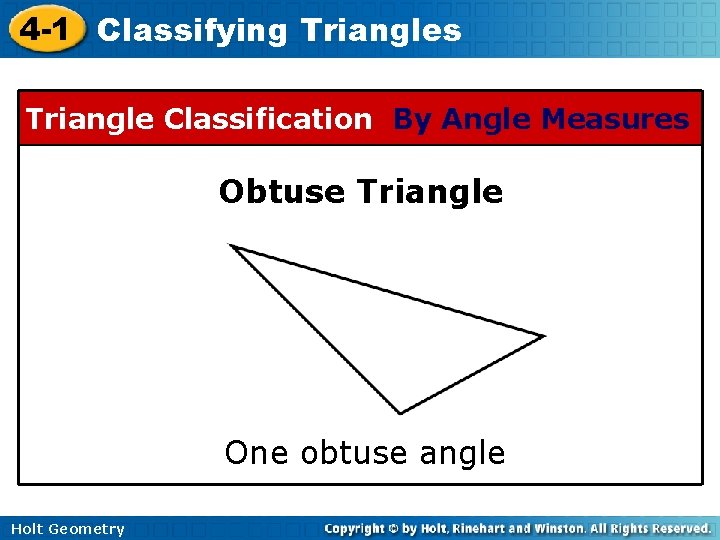
4 -1 Classifying Triangles Triangle Classification By Angle Measures Obtuse Triangle One obtuse angle Holt Geometry

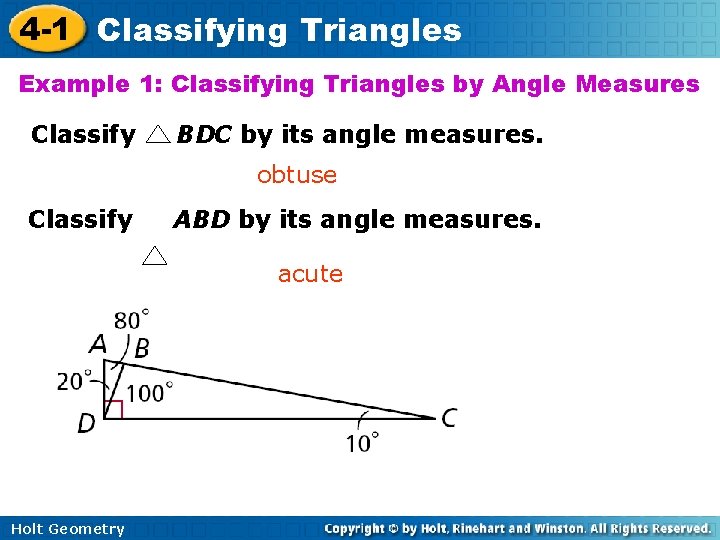
4 -1 Classifying Triangles Example 1: Classifying Triangles by Angle Measures Classify BDC by its angle measures. obtuse Classify ABD by its angle measures. acute Holt Geometry

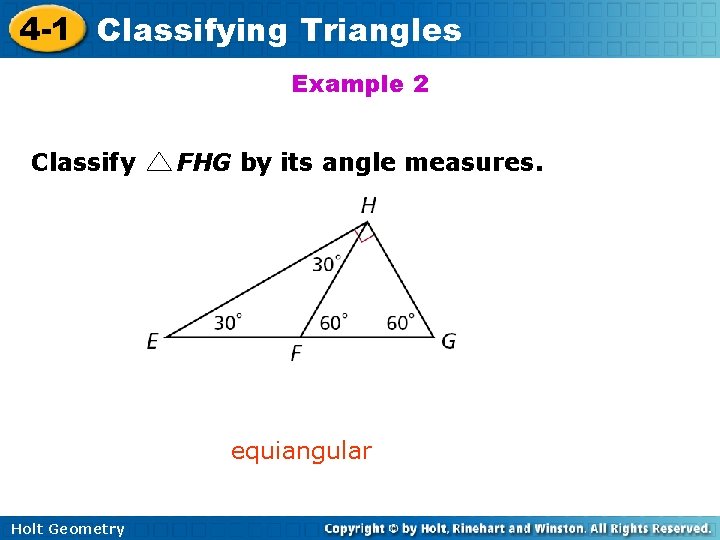
4 -1 Classifying Triangles Example 2 Classify FHG by its angle measures. equiangular Holt Geometry

4 -1 Classifying Triangles Triangle Classification By Side Lengths Equilateral Triangle Three congruent sides Holt Geometry

4 -1 Classifying Triangles Triangle Classification By Side Lengths Isosceles Triangle At least two congruent sides Holt Geometry

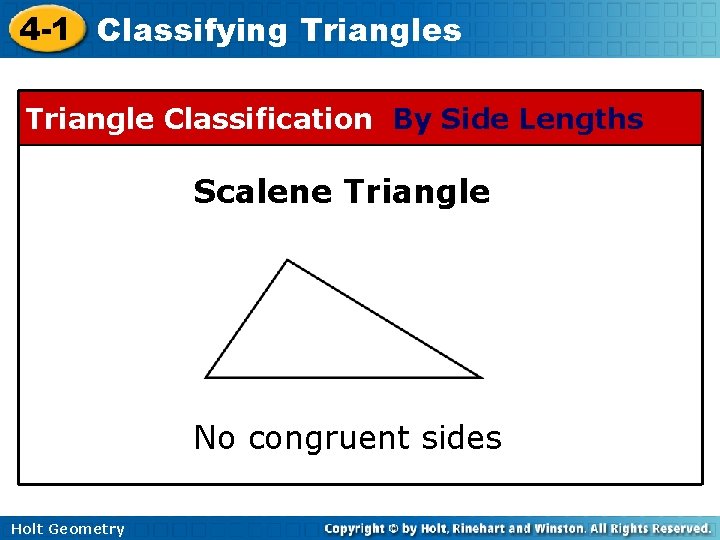
4 -1 Classifying Triangles Triangle Classification By Side Lengths Scalene Triangle No congruent sides Holt Geometry

4 -1 Classifying Triangles Remember! When you look at a figure, you cannot assume segments are congruent based on appearance. They must be marked as congruent. Holt Geometry

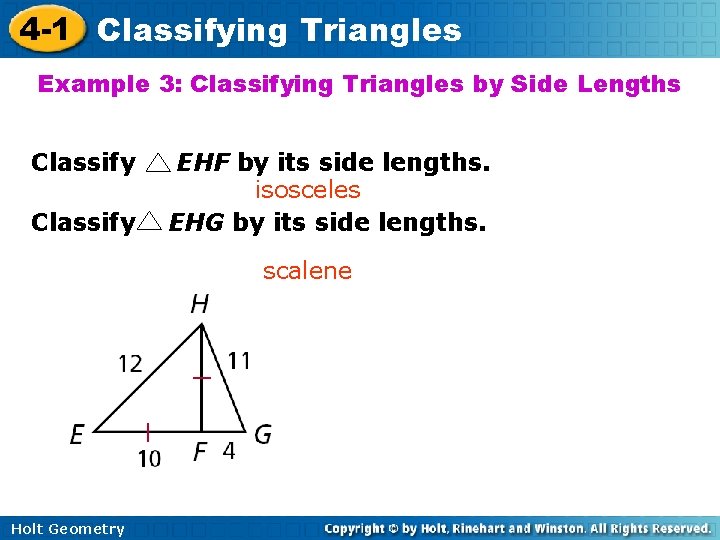
4 -1 Classifying Triangles Example 3: Classifying Triangles by Side Lengths Classify EHF by its side lengths. isosceles EHG by its side lengths. scalene Holt Geometry

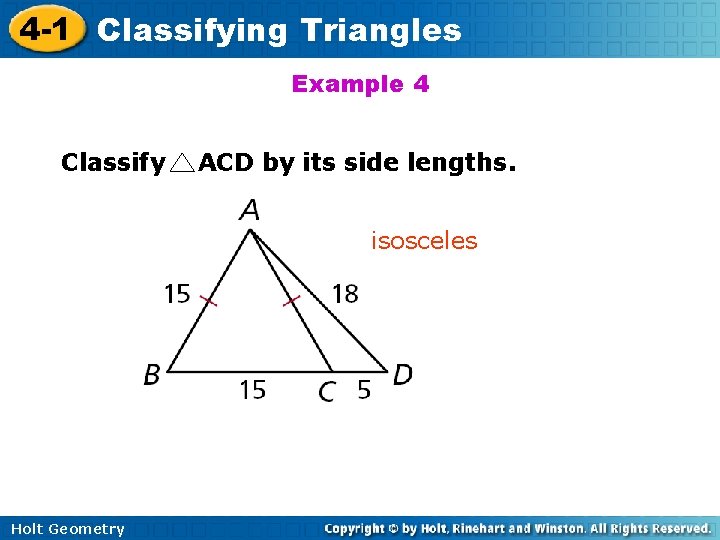
4 -1 Classifying Triangles Example 4 Classify ACD by its side lengths. isosceles Holt Geometry

4 -1 Classifying Triangles Example 5: Using Triangle Classification Find the side lengths of JK=KL=23. 3 JL = 44. 5 Holt Geometry JKL.

4 -1 Classifying Triangles Example 6 Find the side lengths of equilateral All = 17 Holt Geometry FGH.

4 -1 Classifying Triangles Example 7: Application A steel mill produces roof supports by welding pieces of steel beams into equilateral triangles. Each side of the triangle is 18 feet long. How many triangles can be formed from 420 feet of 7 steel beam? Holt Geometry

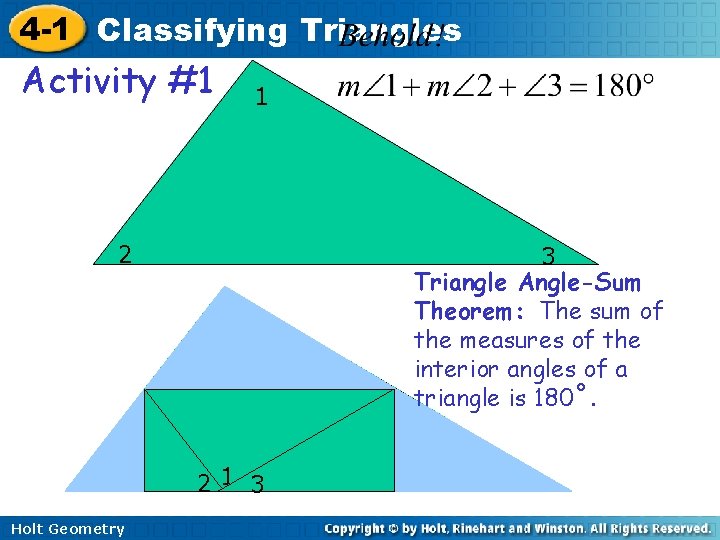
4 -1 Classifying Triangles Activity #1 1 2 3 Triangle Angle-Sum Theorem: The sum of the measures of the interior angles of a triangle is 180˚. 21 3 Holt Geometry

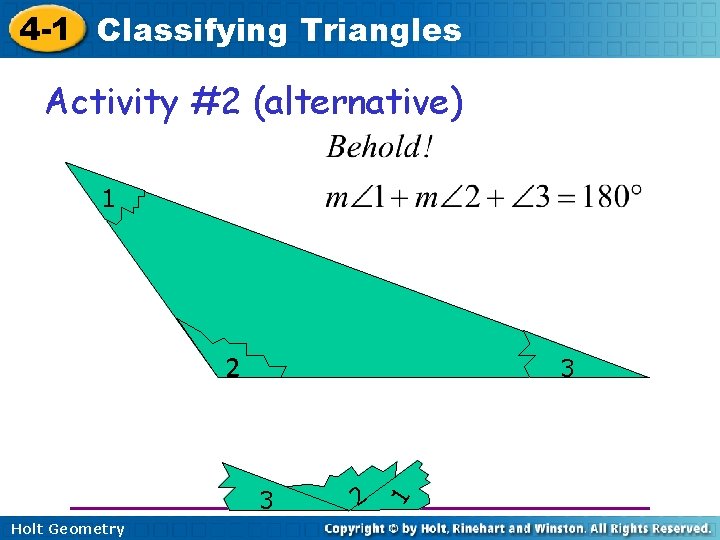
4 -1 Classifying Triangles Activity #2 (alternative) 1 2 3 Holt Geometry 2 1 3

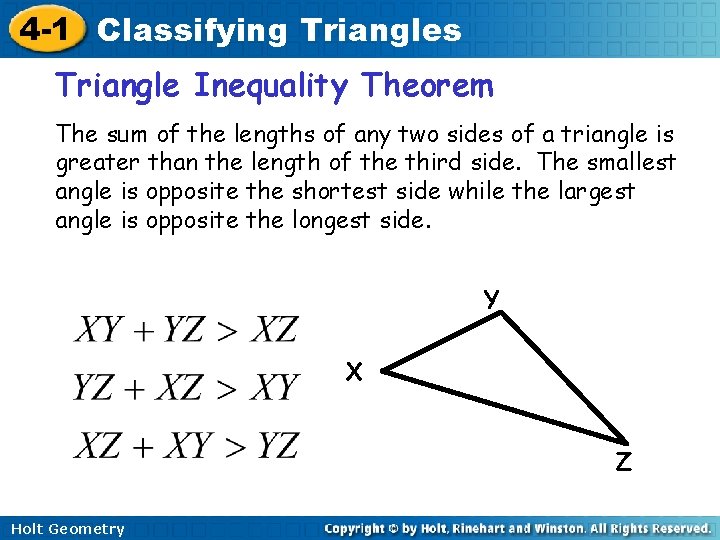
4 -1 Classifying Triangles Triangle Inequality Theorem The sum of the lengths of any two sides of a triangle is greater than the length of the third side. The smallest angle is opposite the shortest side while the largest angle is opposite the longest side. Y X Z Holt Geometry

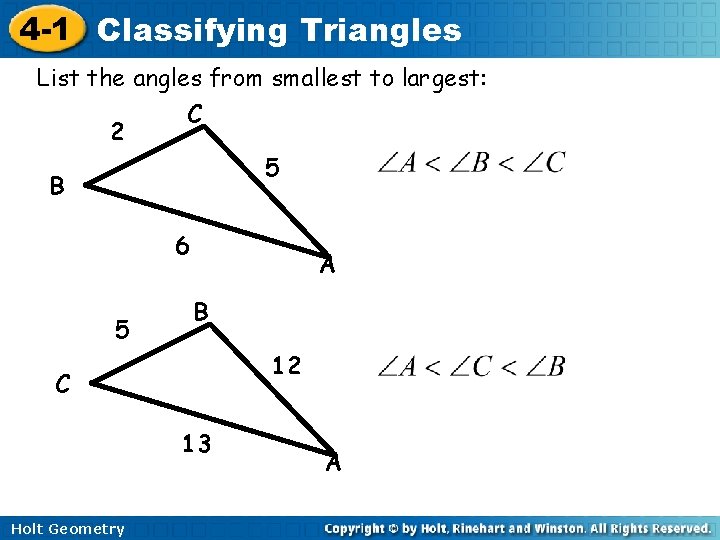
4 -1 Classifying Triangles List the angles from smallest to largest: 2 C 5 B 6 5 A B 12 C 13 Holt Geometry A

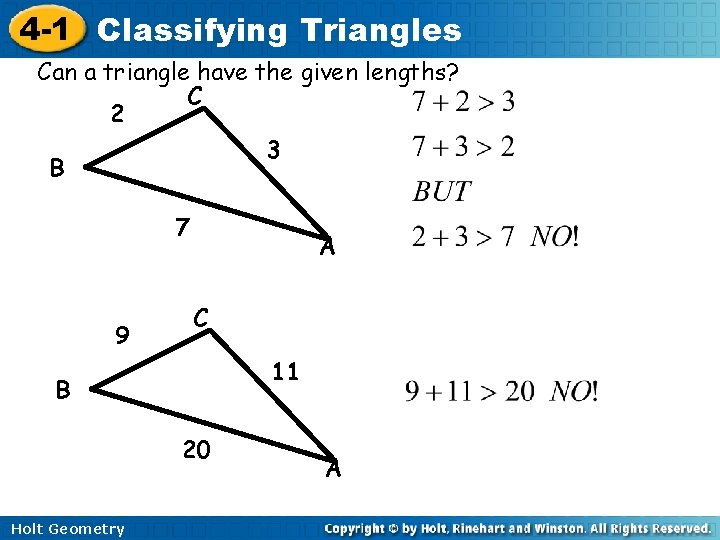
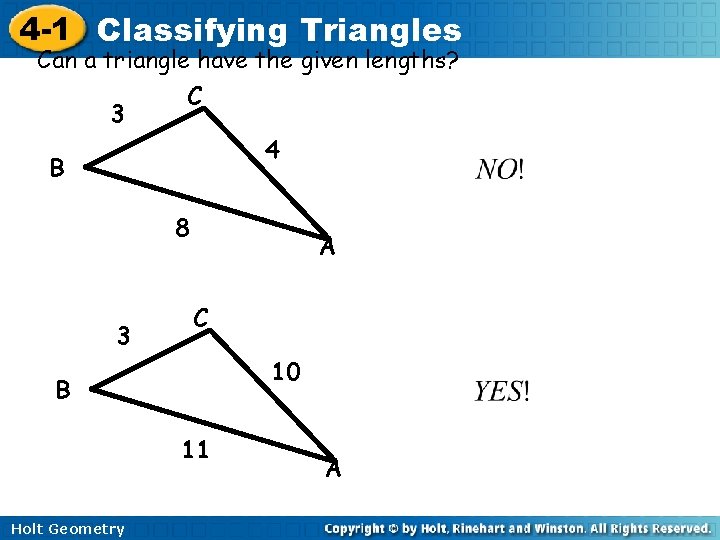
4 -1 Classifying Triangles Can a triangle have the given lengths? C 2 3 B 7 9 A C 11 B 20 Holt Geometry A

4 -1 Classifying Triangles Can a triangle have the given lengths? 3 C 4 B 8 3 A C 10 B 11 Holt Geometry A

4 -1 Classifying Triangles Describe possible lengths for the third side: 9, 12 Holt Geometry

4 -1 Classifying Triangles Describe possible lengths for the third side: 4, 15 3, 4 Holt Geometry

4 -1 Classifying Triangles Classify by Angles 60 ˚ 60 60 ˚ ˚ Equiangular Acute Right Classify by Sides Equilateral Holt Geometry Isosceles Scalene Obtuse

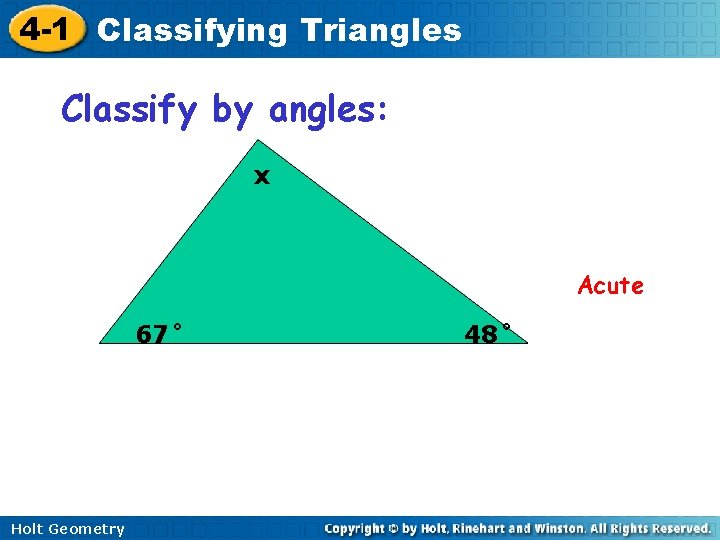
4 -1 Classifying Triangles Classify by angles: x Acute 67˚ Holt Geometry 48˚

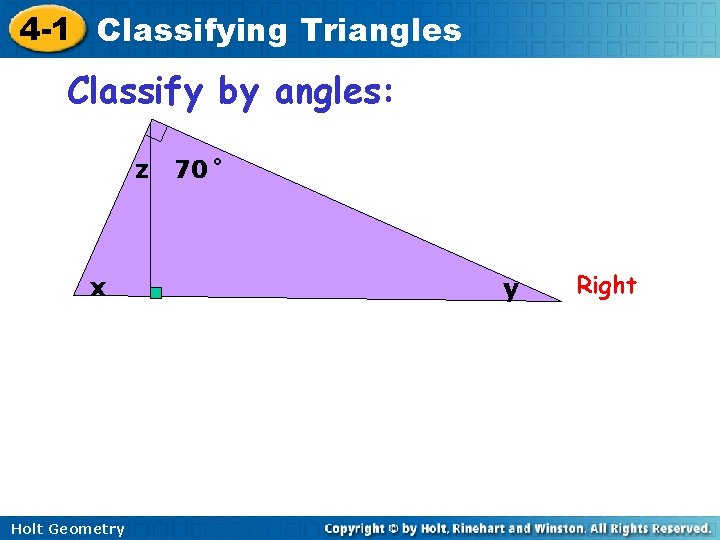
4 -1 Classifying Triangles Classify by angles: z x Holt Geometry 70˚ y Right

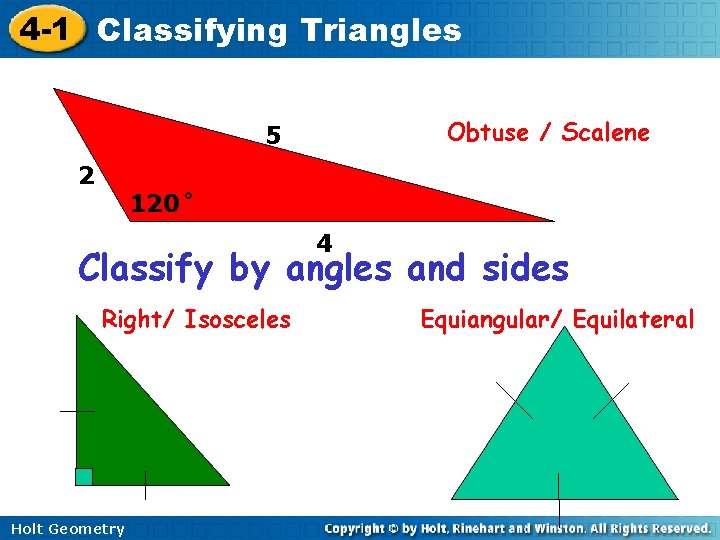
4 -1 Classifying Triangles Obtuse / Scalene 5 2 120˚ 4 Classify by angles and sides Right/ Isosceles Holt Geometry Equiangular/ Equilateral

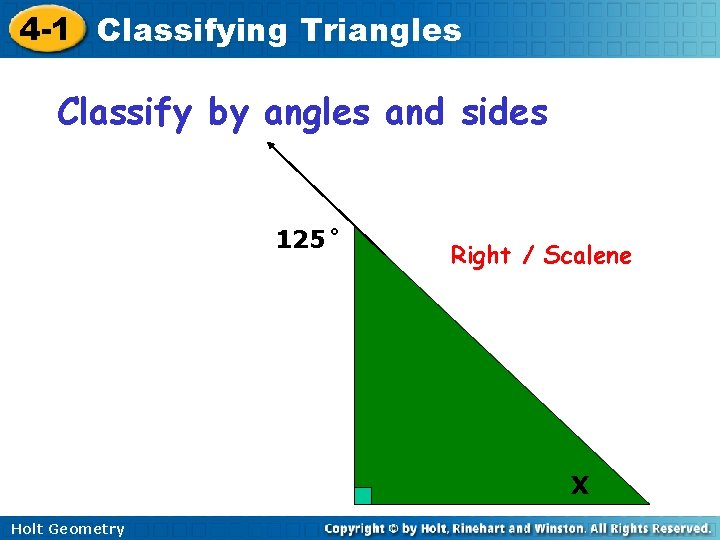
4 -1 Classifying Triangles Classify by angles and sides 125˚ Right / Scalene X Holt Geometry

4 -1 Classifying Triangles A triangle with a 90˚ angle has sides that are 3 cm, 4 cm, and 5 cm long. Classify the triangle by its angles and sides. Right / Scalene Holt Geometry

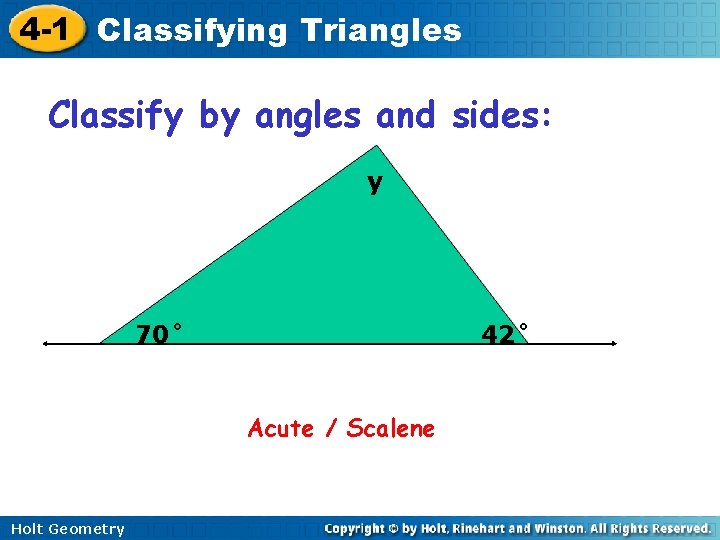
4 -1 Classifying Triangles Classify by angles and sides: y 70˚ 42˚ Acute / Scalene Holt Geometry

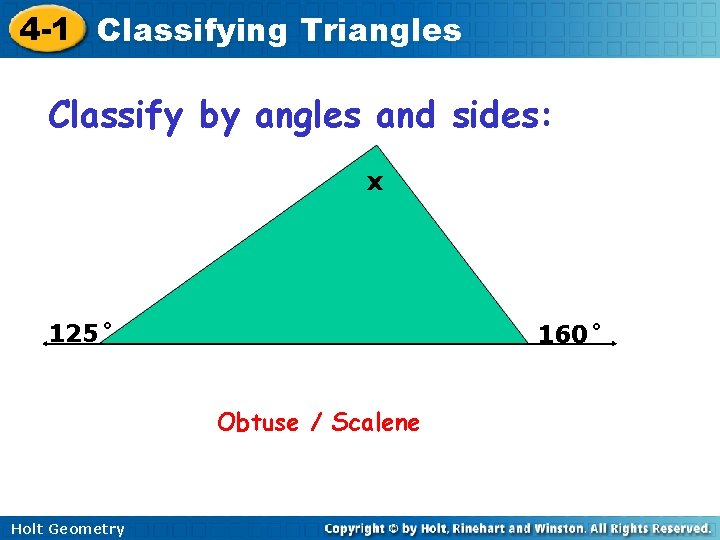
4 -1 Classifying Triangles Classify by angles and sides: x 125˚ 160˚ Obtuse / Scalene Holt Geometry