Chapter 1 Introduction to Probability Statistics Objectives This

Chapter # 1 Introduction to Probability & Statistics

Objectives This course introduces Statistical Techniques & Computer theory in order to facilitate understanding and analysis of Computer models and policies. The emphasis is on applications of various methods and techniques in this the students will also learn about the regression and correlation, index numbers, presentation of data techniques regarding bar charts, Probability distributions and their Computer applications. The aim of this course is to integrate elementary statistical methods and the interpretation of data to analysis applied of current policy importance. To this end students will be provided with an introduction to the basic tools of statistics essential for a proper understanding of Computer Sciences both in the first and subsequent years of study. Students will have the opportunity to practice the application of the analytical and quantitative skills through the medium of selected topics that are developed analyzed in depth.

Course outline 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. Introduction to Probability and Statistics Presenting data Central tendency Dispersion of the data Time series and index no. Probability Binomial Distribution Normal Distribution Sampling theory Confidence intervals Testing of Hypothesis Regression & correlation analysis SPSS

References Reference books Berenson M. L. , Levine D. K. & Krehbiel T. C. , “Basic Business Statistics”, 11/e, Prentice Hall, 2009. 2. Burton G. , Carrol G. & Wall S. , “Quantitative Methods for Business & Economics”, Prentice Hall, 2/e, 2002. 3. Easton & Coll, Statistics Glossary, http: //www. stats. gla. ac. uk/steps/glossary/index. html 4. Kay D. , “Cliffs. AP Statistics”, Wiley Publishing, 2005. 5. Kazmier L. J. , “Business Statistics”, 4/E, Schaum’s Outline Series Mc. GRAW-HILL, 2004. 6. Mc. Clave J. T. , Benson P. G. & Sincich T. , “A First Course in Business Statistics”, 8/e, Prentice Hall, 2000. 7. Render B. , Stair R. M. & Hanna M. E. , “Quantitative Analysis for Management”, 8/e, Prentice Hall, 2003. 8. Tanis E. A. , “Statistics I: Descriptive Statistics and Probability”, HJB, 1987. 9. Triola M. F. , “Elementary Statistics”, 9/e, Addison Wesley, 2005. 10. Wates D. , “Quantitative Methods for Business”, 4/e, Prentice Hall, 2008. 11. Wikipedia, http: //en. wikipedia. org/ 1.

Learing Objectives Understand be able to apply the concept of graphs. Understand the importance of Probability and Statistics for business efficiency and productivity. Be able to implement regression and correlation methods. Understand the importance and use of index number and sampling Understand concept of probability in business development. Know different techniques to develop formulas required for averaging. Be able to provide guidance on: Regression and correlation Probability Application of index numbers, time series and hypothesis

Statistics & Probability Analysis Input Raw Data Process Quantitative Analysis Output Meaningful Information IPO (Input-Process-Output) is one of the most fundamental design patterns. Statistics & Probability Analysis is a scientific approach to managerial decision making whereby raw data are processed and manipulated resulting in meaningful information. Quantitative analysis provides data-driven analytical services for a range of business challenges, specializing in statistical models for site selection decisions. Examples: When to order additional new meterial? What is the total annual cost? What is the safety stock lavel?

The Statistics & Probability Analysis Approach Defining the Problem Developing a Model Acquiring Input Data Developing a Solution Testing the Solution Analyzing the Results Implementing the Results

Quantitative & Qualitative Factors The data; may be quantitative, with values expressed numerically may be qualitative, with characteristics such as consumer preferences being tabulated. Quantitative factors might be different investment alternatives, interest rates, inventory levels, demand, or labor cost. Qualitative factors such as the weather, state and federal legislation, and technology breakthroughs should also be considered.

Statistics It is the science of collection, presentation, summarization, analysis and interpretation of numerical data. A branch of mathematics taking and transforming numbers into useful information for decision makers. Statistics is the art of learning from data. Methods for processing & analyzing numbers. Methods for helping reduce the uncertainty inherent in decision making. Statistics refers to the body of techniques used for collecting, organizing, analyzing, and interpreting data. A statistic is a quantity that is calculated from a sample of data. It is used to give information about unknown values in the corresponding population.

Why we Learn Statistics & Probability? • Business memos • Business research • Technical reports • Technical journals • Newspaper articles • Magazine articles • Make reliable forecasts about a business activity • Improve business processes • Present and describe business data and information properly

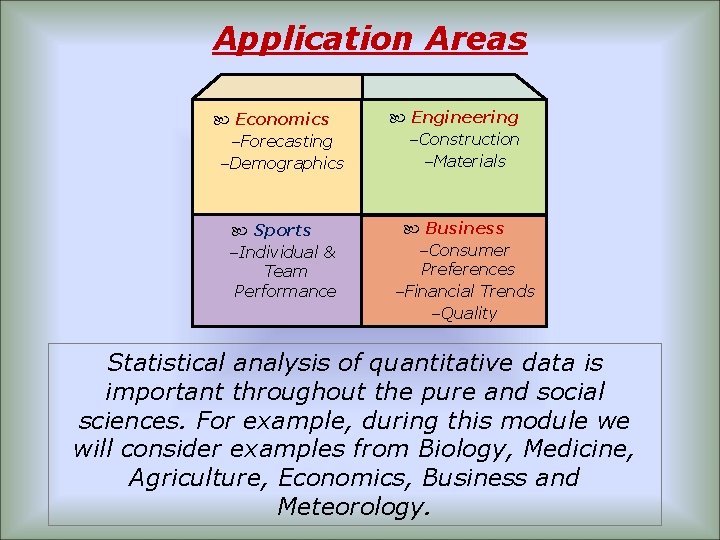
Application Areas Economics -Forecasting -Demographics Sports -Individual & Team Performance Engineering -Construction -Materials Business -Consumer Preferences -Financial Trends -Quality Statistical analysis of quantitative data is important throughout the pure and social sciences. For example, during this module we will consider examples from Biology, Medicine, Agriculture, Economics, Business and Meteorology.

Statistics Business statistics is the science of good decision making in the face of uncertainty and is used in many disciplines such as financial analysis, econometrics, auditing, production and operations including services improvement, and marketing research. Statistics is used in business to help make better decisions by understanding the sources of variation and by uncovering patterns and relationships in business data.

Types of Statistics Descriptive That branch of statistics where we describe the methods of Collecting, summarizing, analyzing and describing data Inferential That branch of statistics which is responsible for Drawing conclusions and/or making decisions concerning a population based only on sample data

Descriptive Statistics Descriptive statistic can be defined as collection, presentation, and characterization of a set of data in order to describe properly the various features of that set of data. • Collect data e. g. , Survey • Present data e. g. , Tables and graphs • Characterize data e. g. , Sample mean =.

Inferential Statistics? Inferential statistics can be defined as estimation of a characteristics of a population or the making of a decision concerning a population based only on sample results. • Estimation e. g. , Estimate the population mean weight using the sample mean weight • Hypothesis testing e. g. , Test the claim that the population mean weight is 120 pounds

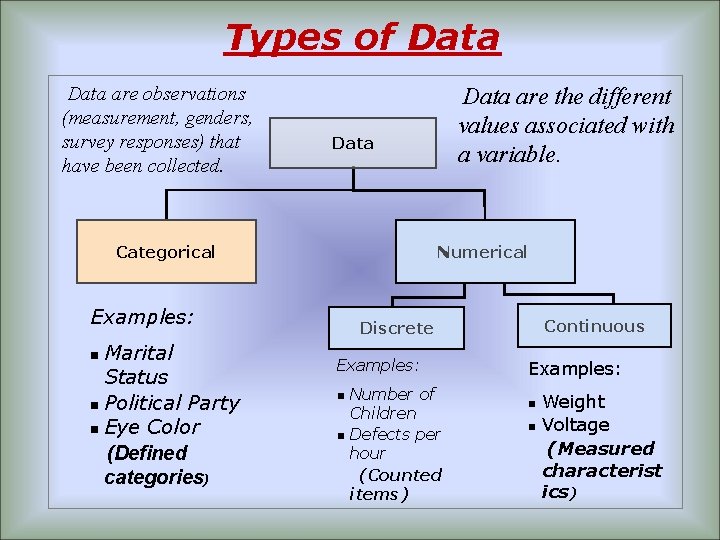
Types of Data are observations (measurement, genders, survey responses) that have been collected. Data Categorical Numerical Examples: Marital Status n Political Party n Eye Color (Defined categories) n Data are the different values associated with a variable. Continuous Discrete Examples: n n Number of Children Defects per hour (Counted items) Examples: Weight n Voltage (Measured characterist ics) n

Nominal Data A set of data is said to be nominal if the values / observations belonging to it can be assigned a code in the form of a number where the numbers are simply labels. • You can count but not order or measure nominal data. • Ordinal Data A set of data is said to be ordinal if the values / observations belonging to it can be ranked (put in order) or have a rating scale attached. • You can count and order, but not measure, ordinal data. •

Variable Types of Variables A variable is a characteristic of an item or individual. Variables Categorical (qualitative) variables have values that can only be placed into categories, such as “yes” and “no. ” Numerical (quantitative) variables have values that represent quantities. i- Continuous variable ii-Discontinuous variable iii- Independent variable iv- Dependent variable v- Endogenous variable vi- Exogenous variable vii- Quantitative variable viii- Qualitative variable Variables are either qualitative or quantitative. Qualitative variables have non-numeric outcomes, with no natural ordering. For example, gender, disease status, and type of car are all qualitative variables. Quantitative variables have numeric outcomes. For example, survival time, height, age, number of children, and number of faults are all quantitative variables.

Quantitative variables can be discrete or continuous. Discrete random variables have outcomes which can take only a countable number of possible values. These possible values are usually taken to be integers, but don’t have to be. ◦ For example, number of children and number of faults are discrete random variables which take only integer values, but your score in a quiz where “half” marks are awarded is a discrete quantitative random variable which can take on non-integer values. Continuous random variables can take any value over some continuous scale. ◦ For example, survival time and height are continuous random variables. Often, continuous random variables are rounded to the nearest integer, but the are still considered to be continuous variables if there is an underlying continuous scale. Age is a good example of this.

Population A census is the collection of data from every A population is any entire collection of member of the population. people, animals, plants or things from which we may collect data. It is the entire group we are interested in, which we wish to describe or draw conclusions about. Example The population for a study of infant health might be all children born in the UK in the 1980's. The sample might be all babies born on 7 th May in any of the years. Constant The values which are being held constant. OR A symbol or characteristic which does not vary from an individual to another individual known as constant Parameters Coefficient The values which are being calculated from the population when the entire population is given. OR The values which are being kept constant during a specific sort of discussion when the discussion pattern change these values change. The numerical value associated with the independent variable to show the change in dependent variable. It is also known as slope / rate of change / derivative of the function.

Sample A sample is a group of units selected from a larger group (the population). By studying the sample it is hoped to draw valid conclusions about the larger group. A sample is generally selected for study because the population is too large to study in its entirety. The sample should be representative of the general population. This is often best achieved by random sampling. Also, before collecting the sample, it is important that the researcher carefully and completely defines the population, including a description of the members to be included. Example The population for a study of infant health might be all children born in the UK in the 1980's. The sample might be all babies born on 7 th May in any of the years.

Primary Data Raw data is a term for data collected from a source. Raw data has not been subjected to processing or any other manipulation, and are also referred to as primary data. Raw data is a relative term. Information in raw or unorganized form (such as alphabets, numbers, or symbols) that refer to, or represent, conditions, ideas, or objects. Data is limitless and present everywhere in the universe. Data observed or collected directly from first-hand experience. When someone refers to "primary data" they are referring to data collected by the researcher himself/herself. This is data that has never been gathered before, whether in a particular way, or at a certain period of time. Researchers tend to gather this type of data when what they want cannot be find from outside sources. You can tailor your data questions and collection to fit the need of your research questions. This can be an extremely costly task and, if associated with a college or institute, requires permission and authorization to collect such data. Issues of consent and confidentiality are of extreme importance. Sources of primary data i- Interview iii- Action research v- Life histories vii- Ethnographic research ii- Observation iv- Case studies vi- Questionnaires viii- Longitudinal studies

Secondary Data If the time or hassle of collecting your own data is too much, or the data collection has already been done, secondary data may be more appropriate for your research. This type of data typically comes from other studies done by other institutions or organizations. There is no less validity with secondary data, but you should be well informed about how it was collected. There a number of free services online as well as many other made available through your current status as BYU students. Secondary data, is data collected by someone other than the user. Secondary data analysis saves time that would otherwise be spent collecting data and, particularly in the case of quantitative data, provides larger and higher-quality databases Secondary data sources i- Previous research iii- Mass media products v- Letters vii- Web information ii- Official statistics iv- Diaries vi- Government reports viii- Historical data and information