Solving Equations with Solving Equations 10 3 Variables

Solving Equations with Solving Equations 10 -3 Variables on Both Sides Warm Up Problem of the Day Lesson Presentation Pre-Algebra
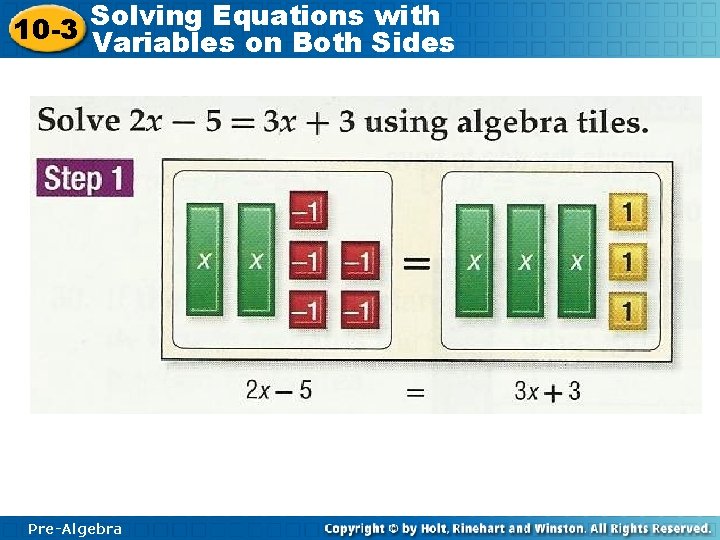
Solving Equations with 10 -3 Variables on Both Sides Pre-Algebra
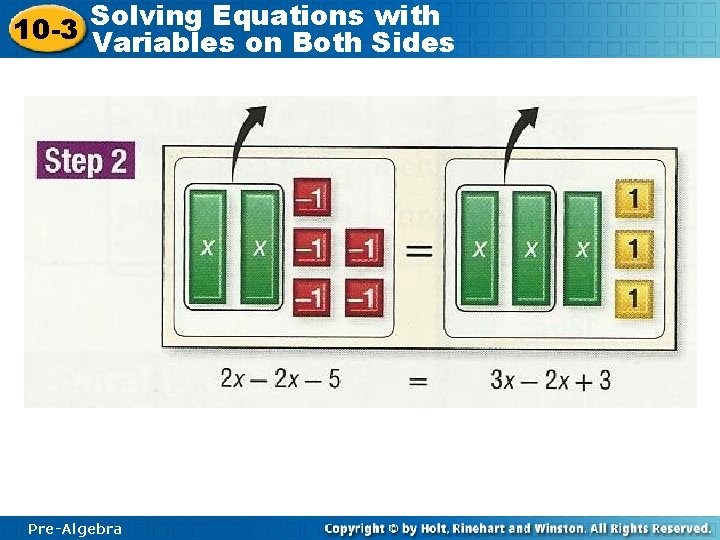
Solving Equations with 10 -3 Variables on Both Sides Pre-Algebra
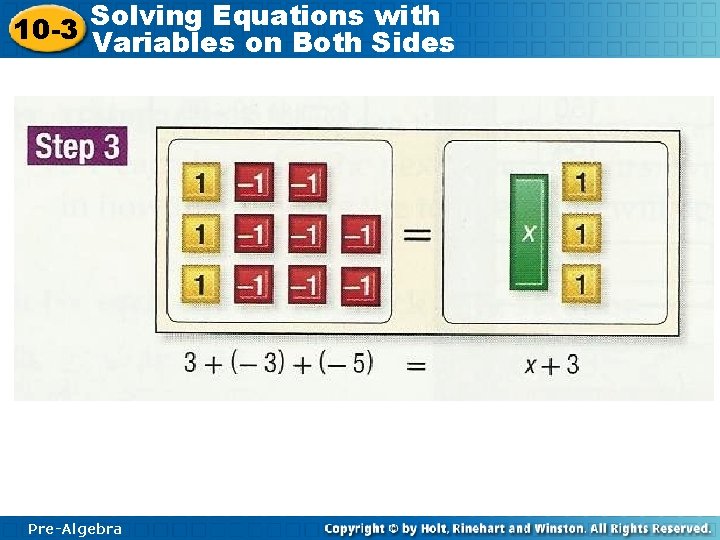
Solving Equations with 10 -3 Variables on Both Sides Pre-Algebra
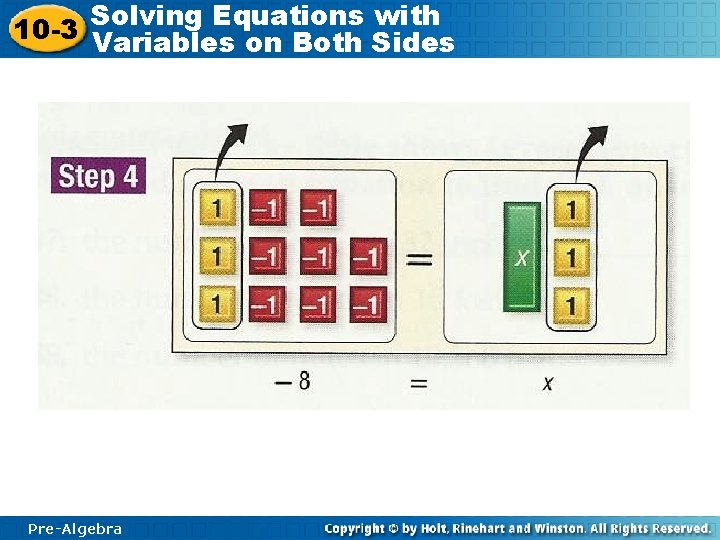
Solving Equations with 10 -3 Variables on Both Sides Pre-Algebra

Solving Equations with 10 -3 Variables on Both Sides Pre-Algebra

Solving Equations with 10 -3 Variables on Both Sides • What are some observations you made about solving equations with variables on both sides, based on last night’s homework? • Goal is to isolate the variable – get variables on one side and numbers on the other. • You can go in different order. There are different ways to go about the problem. Pre-Algebra

Solving Equations with 10 -3 Variables on Both Sides What can NOT do? Ex A) 4 x + 6 = x – 4 x 6 = – 3 x – 3 – 2 = x Pre-Algebra 4 x + 6 = x –x -6 – x 3 x = – 6 3 3 x = -2 -6

Solving Equations with 10 -3 Variables on Both Sides Ex B) 9 b – 6 = 5 b + 18 – 5 b 4 b – 6 = 18 +6 +6 4 b = 24 4 4 b=6 Pre-Algebra

Solving Equations with 10 -3 Variables on Both Sides With each step, you are keeping the equation, ajd just simplifying. If your final answer turns out to be not true, there is NO SOLUTION that would work for this equation. Ex. C) 9 w + 3 = 5 w + 7 + 4 w 9 w + 3 = 9 w + 7 – 9 w 3≠ 7 No solution. There is no number that can be substituted for the variable w to make the equation true. Pre-Algebra

Solving Equations with 10 -3 Variables on Both Sides Ex. D y 3 y 3 7 + – =y– 5 5 10 4 ( ) Multiply by the LCD. 7 y 3 3 y 20(5 ) + 20( 5 ) – 20(4 )= 20(y) – 20( 10) 20 y 3 y + – 3 5 5 4 7 = 20 y – 10 4 y + 12 y – 15 = 20 y – 14 16 y – 15 = 20 y – 14 Pre-Algebra Combine like terms.

Solving Equations with 10 -3 Variables on Both Sides 16 y – 15 = 20 y – 14 – 16 y – 15 = 4 y – 14 + 14 – 1 = 4 y 4 4 -1 = y 4 Pre-Algebra + 14 Subtract 16 y from both sides. Add 14 to both sides. Divide both sides by 4.

Solving Equations with 10 -3 Variables on Both Sides Ex. E) 12 z – 12 – 4 z = 6 – 2 z + 32 8 z – 12 = – 2 z + 38 + 2 z 10 z – 12 = + 38 + 12 +12 10 z = 50 10 z 50 = 10 10 z=5 Pre-Algebra

Solving Equations with 10 -3 Variables on Both Sides Additional Example 3: Consumer Application Jamie spends the same amount of money each morning. On Sunday, he bought a newspaper for $1. 25 and also bought two doughnuts. On Monday, he bought a newspaper for fifty cents and bought five doughnuts. On Tuesday, he spent the same amount of money and bought just doughnuts. How many doughnuts did he buy on Tuesday? Pre-Algebra

Solving Equations with 10 -3 Variables on Both Sides Additional Example 3 Continued First solve for the price of one doughnut. d = price of one doughnut. 1. 25 + 2 d = 0. 50 + 5 d – 2 d 1. 25 = 0. 50 + 3 d – 0. 50 0. 75 – 0. 50 = 3 d 0. 75 = 3 d 3 3 0. 25 = d Pre-Algebra The price of one doughnut is $0. 25.

Solving Equations with 10 -3 Variables on Both Sides Additional Example 3 Continued Now find the amount of money Jamie spends each morning. Choose one of the original 1. 25 + 2 d expressions. 1. 25 + 2(0. 25) = 1. 75 Jamie spends $1. 75 each morning. Find the number of doughnuts Jamie buys on Tuesday. Let n represent the 0. 25 n = 1. 75 number of doughnuts. 0. 25 n = 1. 75 Divide both sides by 0. 25 n = 7; Jamie bought 7 doughnuts on Tuesday. Pre-Algebra
- Slides: 16