Simple Linear Correlation Correlation Degree of linear association

Simple Linear Correlation

Correlation • Degree of linear association between the two variables is define as simple correlation – Correlation is only concerned with strength of the relationship – No causal effect is implied with correlation

The population correlation coefficient ρ (rho) measures the strength of the association between the variables The sample correlation coefficient r is an estimate of ρ and is used to measure the strength of the linear relationship in the sample observations

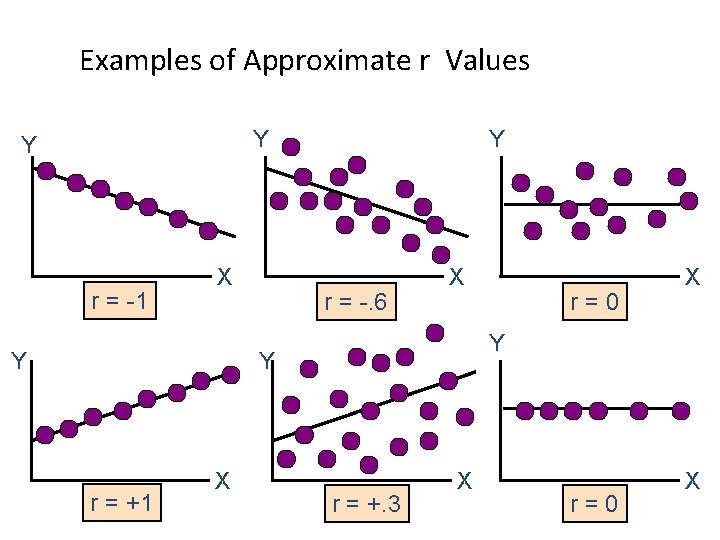
Features of ρ and r • Unit free • Range between -1 and 1 • The closer to -1, the stronger the negative linear relationship • The closer to 1, the stronger the positive linear relationship • The closer to 0, the weaker the linear relationship

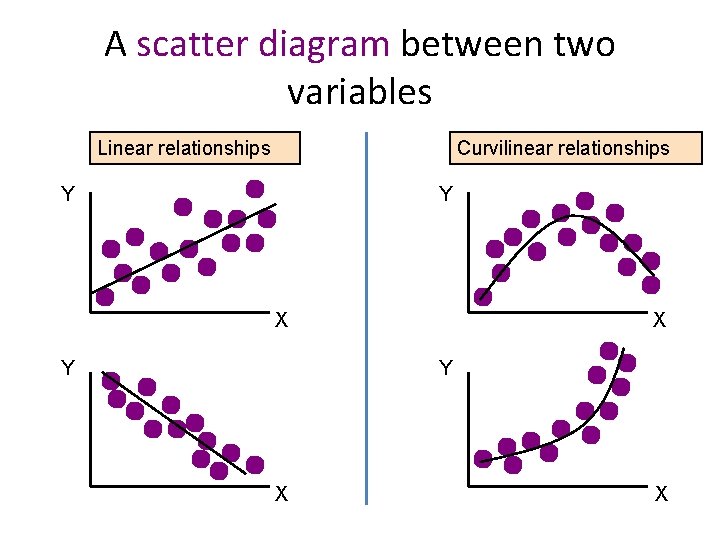
Graphical Method of Correlation The nature of relationship between the two variable can be explained by a simple graphical scatter points. It is the simplest method to assess relationship between two quantitative variables. In other words a scatter diagram can be used to show the direction of the relationship between two variables.

A scatter diagram between two variables Linear relationships Curvilinear relationships Y Y X Y X X

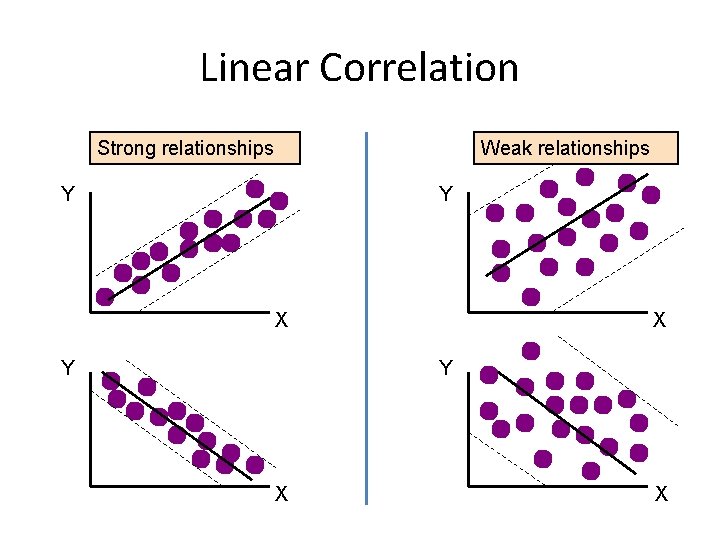
Linear Correlation Strong relationships Weak relationships Y Y X Y X X

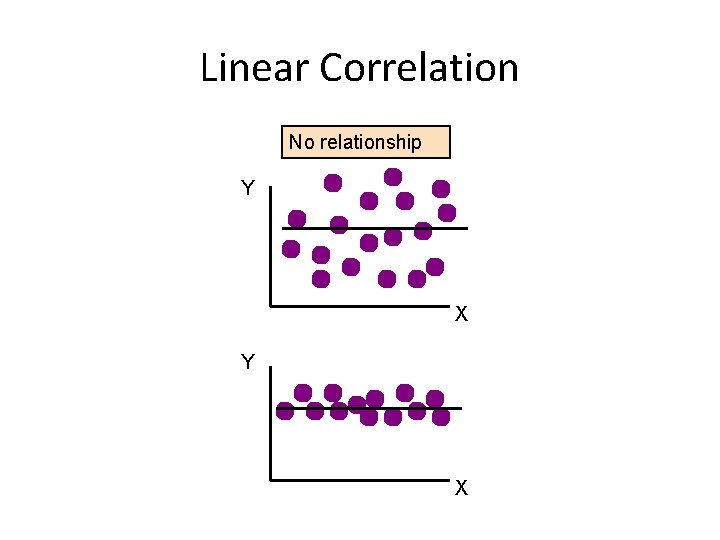
Linear Correlation No relationship Y X

Examples of Approximate r Values Y Y r = -1 X Y Y r = -. 6 X Y Y r = +1 X r=0 X r = +. 3 X r=0 X

Mathematical Method Correlation coefficient n Pearson’s Correlation Coefficient is standardized covariance (unit less):

Mathematical Method Correlation coefficient The correlation coefficient is an index of the degree of association between two variables. It can also be used for comparing the degree of association in different groups For example, we may be interested in knowing whether the degree of association between age and systolic BP is the same (or different) in males and females

Correlation coefficient does not give the rate of change in one variable for changes in the other variable Eg: Age & Systolic BP - Males : r = 0. 7 Females : r = 0. 5 From this one should not conclude that Systolic BP increases at a higher rate among males than females

n Pearson’s Correlation Coefficient is standardized covariance (unit less):

Covariance : Average deviation in two variables (x and y ) from their respective mean

Interpreting Covariance cov(X, Y) > 0 X and Y are positively correlated cov(X, Y) < 0 X and Y are inversely correlated cov(X, Y) = 0 X and Y are independent

Calculating the Correlation Coefficient Sample correlation coefficient: or the algebraic equivalent: where: r = Sample correlation coefficient n = Sample size x = Value of the independent variable y = Value of the dependent variable

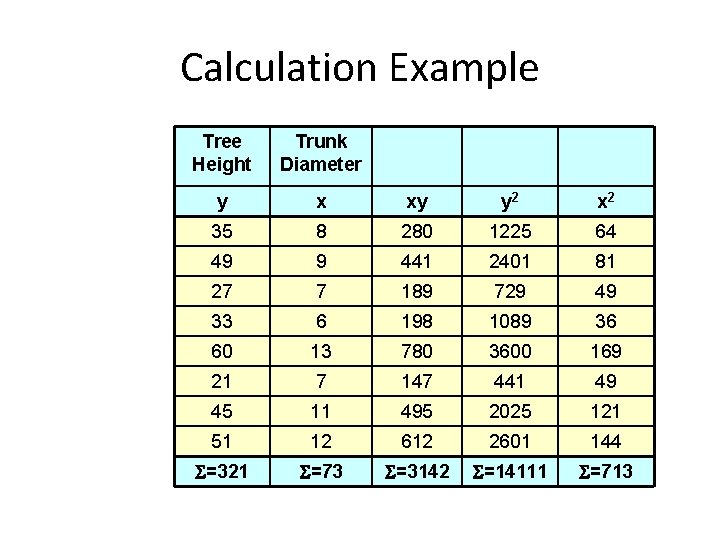
Calculation Example Tree Height Trunk Diameter y x xy y 2 x 2 35 8 280 1225 64 49 9 441 2401 81 27 7 189 729 49 33 6 198 1089 36 60 13 780 3600 169 21 7 147 441 49 45 11 495 2025 121 51 12 612 2601 144 =321 =73 =3142 =14111 =713

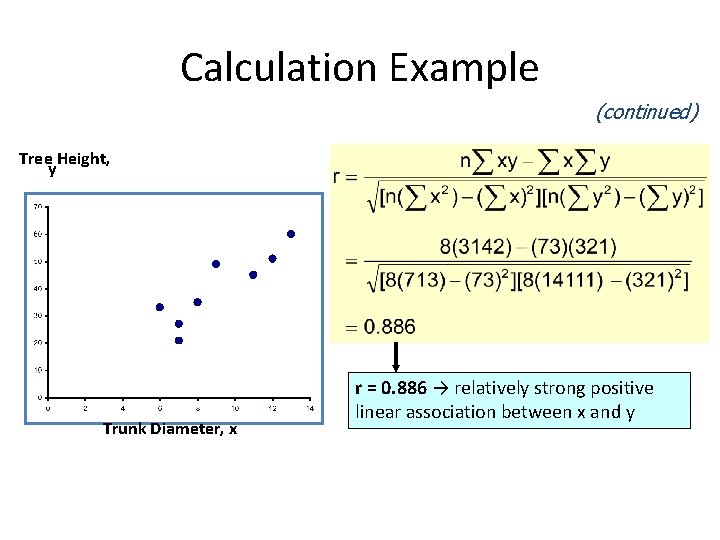
Calculation Example (continued) Tree Height, y Trunk Diameter, x r = 0. 886 → relatively strong positive linear association between x and y

By using the coding data Karl Pearson 'coefficient correlation can compute numerical value of correlation simple

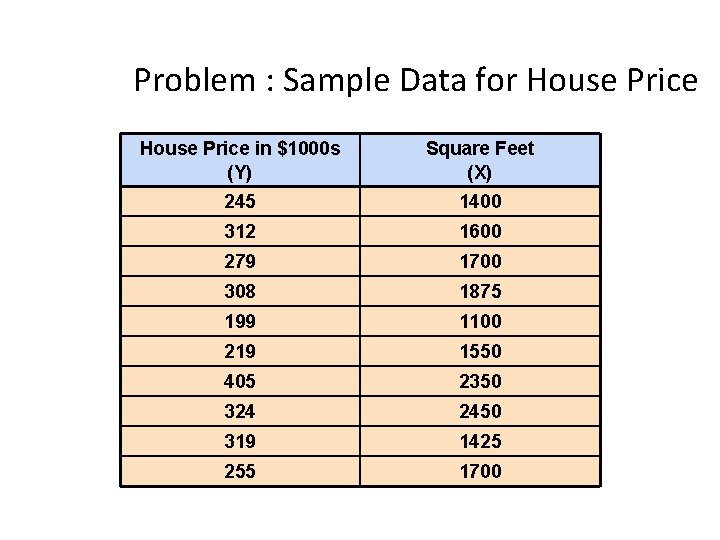
Problem : Sample Data for House Price in $1000 s (Y) Square Feet (X) 245 1400 312 1600 279 1700 308 1875 199 1100 219 1550 405 2350 324 2450 319 1425 255 1700