Degree and Eigenvector Centrality Degree Centrality 2 Degree

Degree and Eigenvector Centrality

Degree Centrality 2

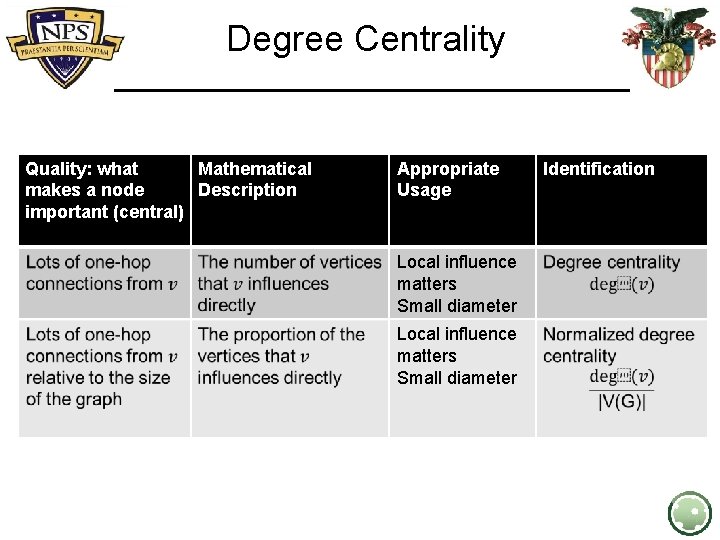
Degree Centrality Quality: what Mathematical makes a node Description important (central) Appropriate Usage Local influence matters Small diameter Identification

Degree Centrality 4

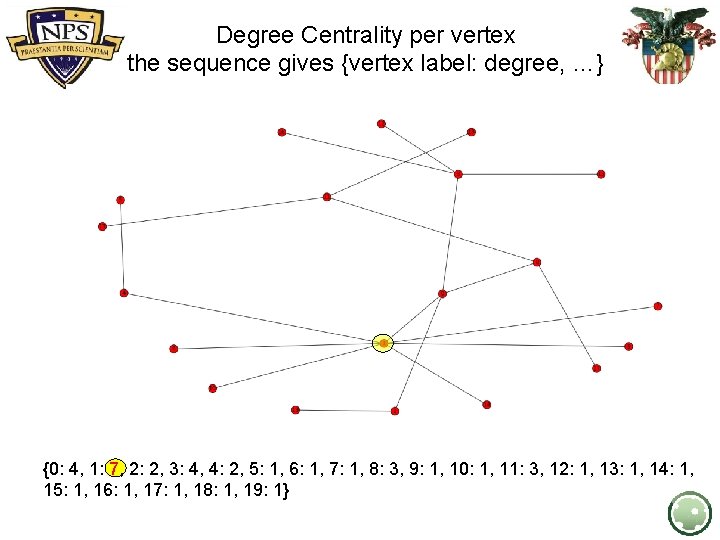
Degree Centrality per vertex the sequence gives {vertex label: degree, …} {0: 4, 1: 7, 2: 2, 3: 4, 4: 2, 5: 1, 6: 1, 7: 1, 8: 3, 9: 1, 10: 1, 11: 3, 12: 1, 13: 1, 14: 1, 15: 1, 16: 1, 17: 1, 18: 1, 19: 1}

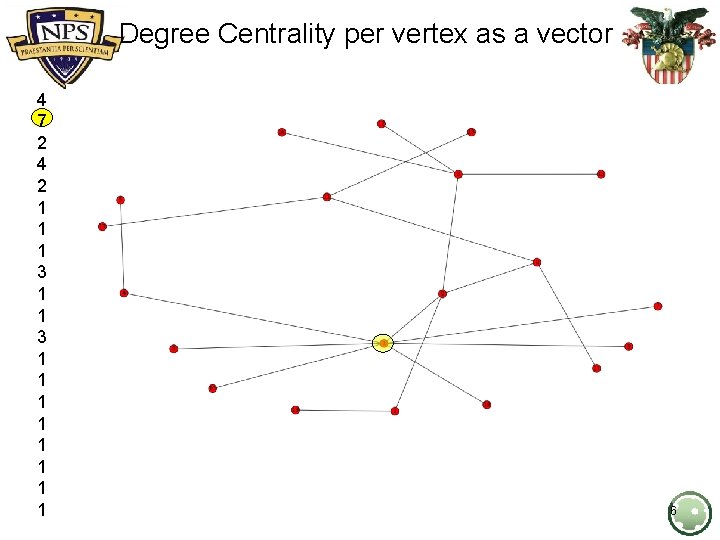
Degree Centrality per vertex as a vector 4 7 2 4 2 1 1 1 3 1 1 1 1 6

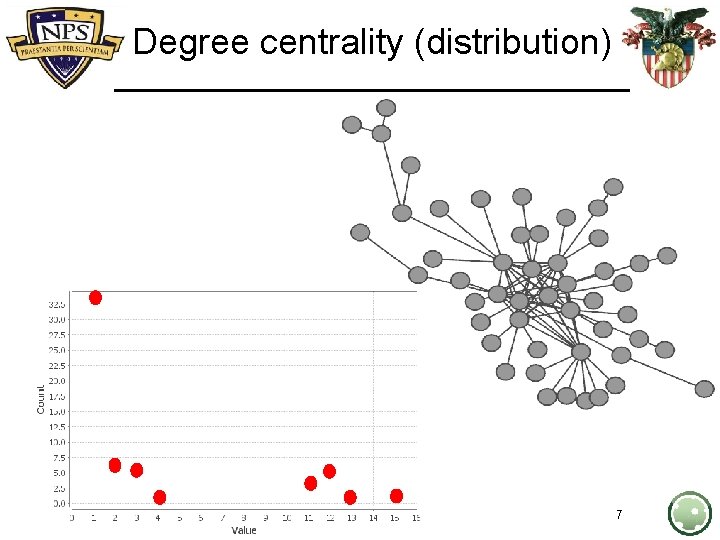
Degree centrality (distribution) 7

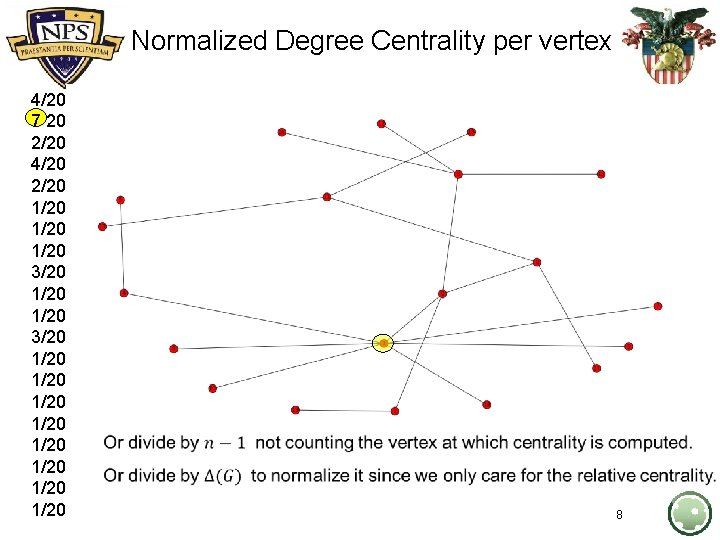
Normalized Degree Centrality per vertex 4/20 7 20 2/20 4/20 2/20 1/20 3/20 1/20 1/20 1/20 8

Eigenvector Centrality 9

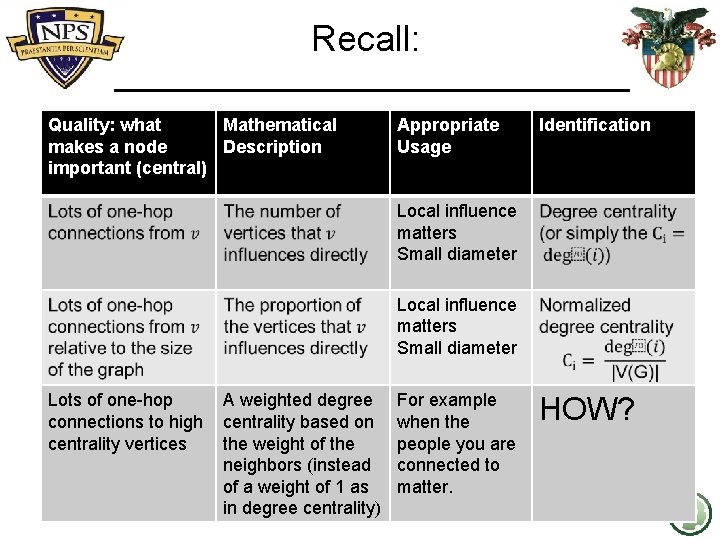
Recall: Quality: what Mathematical makes a node Description important (central) Appropriate Usage Local influence matters Small diameter Lots of one-hop A weighted degree connections to high centrality based on centrality vertices the weight of the neighbors (instead of a weight of 1 as in degree centrality) For example when the people you are connected to matter. Identification

Recall: Quality: what Mathematical makes a node Description important (central) Appropriate Usage Identification Local influence matters Small diameter Lots of one-hop A weighted degree connections to high centrality based on centrality vertices the weight of the neighbors (instead of a weight of 1 as in degree centrality) For example when the people you are connected to matter. HOW?

Recall: Quality: what makes a node important (central) Mathematical Description Appropriate Usage Local influence matters Small diameter Lots of one-hop connections to high centrality vertices A weighted degree centrality based on the weight of the neighbors (instead of a weight of 1 as in degree centrality) For example when the people you are connected to matter. Identification

Eigenvector Centrality • A generalization of the degree centrality: a weighted degree vector that depends on the centrality of its neighbors (rather than every neighbor having a centrality of 1) • How do we find it? By finding the largest eigenvalue and its associated eigenvector (leading eigenvector) of the adjacency matrix. • We will get to the “why eigenvectors work” part. 13

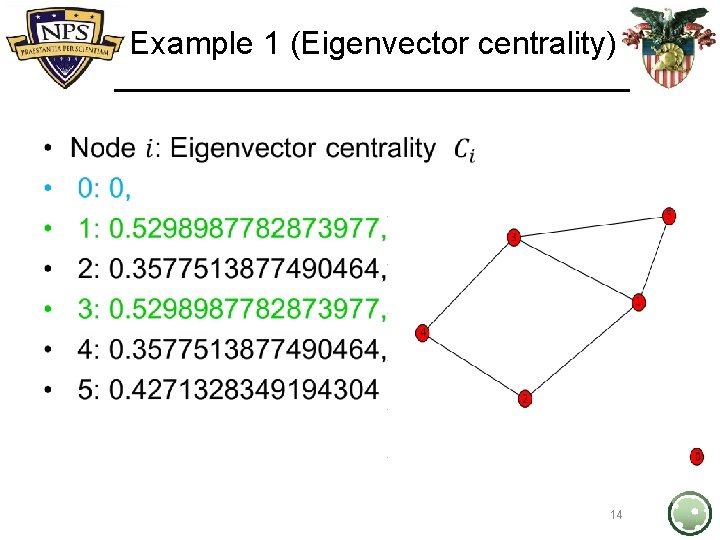
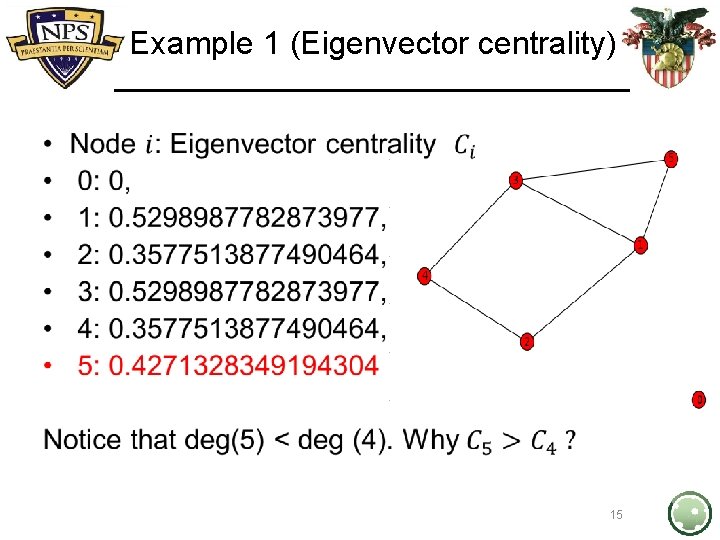
Example 1 (Eigenvector centrality) • 14

Example 1 (Eigenvector centrality) • 15

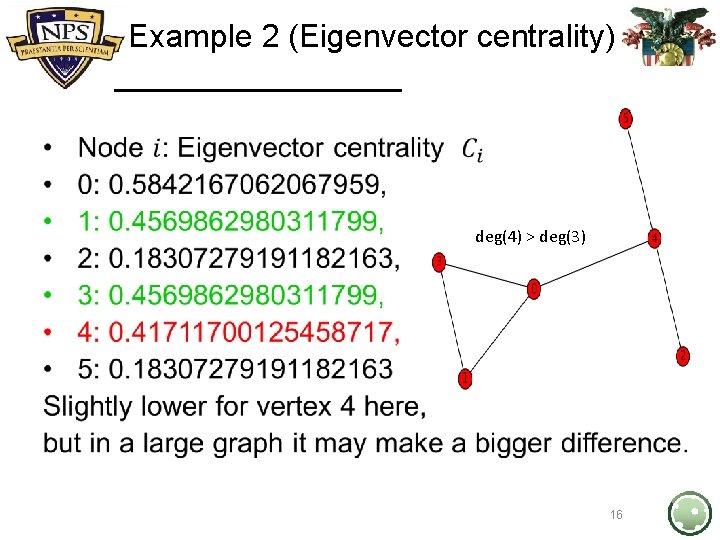
Example 2 (Eigenvector centrality) • deg(4) > deg(3) 16

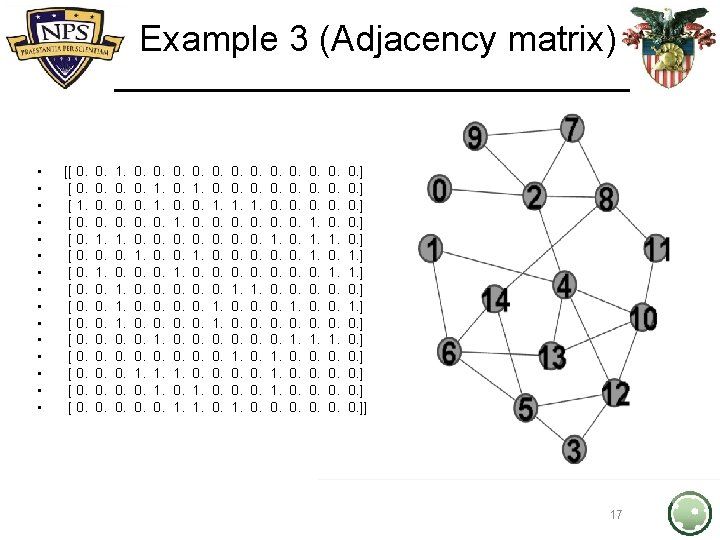
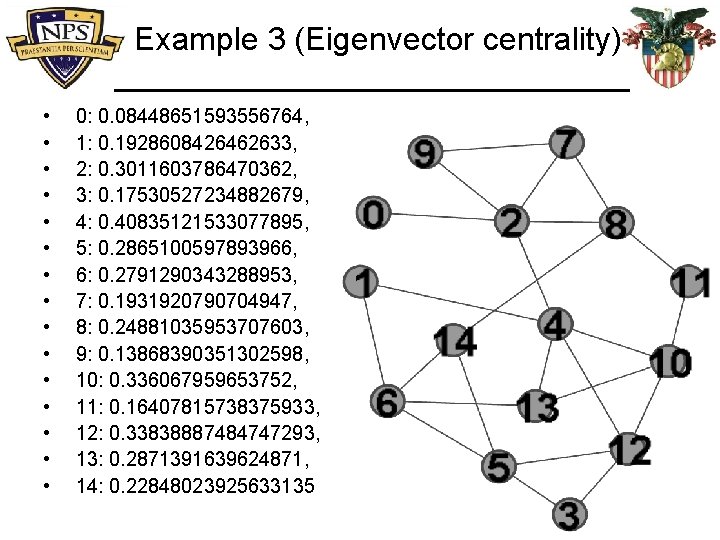
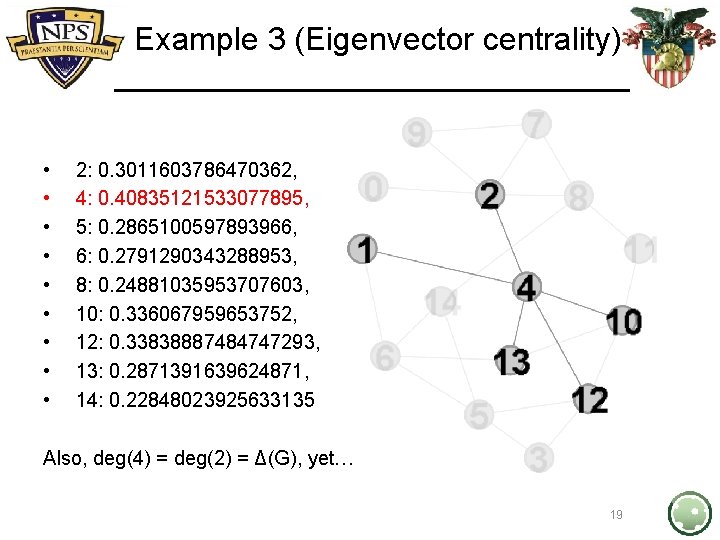
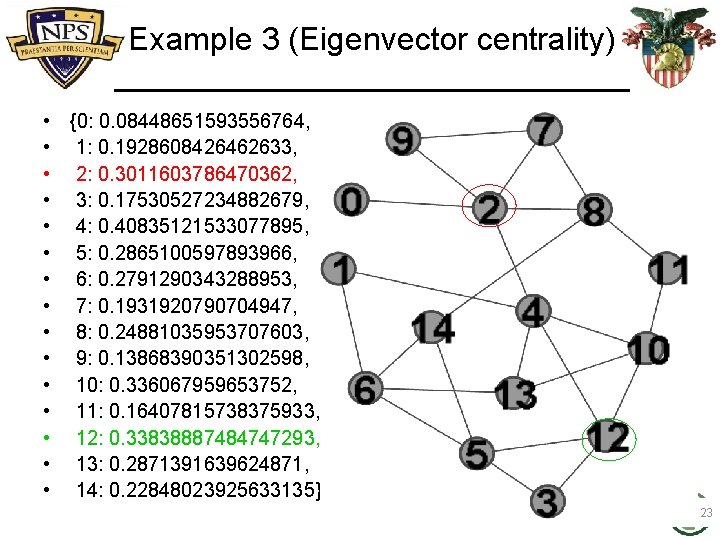
Example 3 (Eigenvector centrality) • • • • 0: 0. 08448651593556764, 1: 0. 1928608426462633, 2: 0. 3011603786470362, 3: 0. 17530527234882679, 4: 0. 40835121533077895, 5: 0. 2865100597893966, 6: 0. 2791290343288953, 7: 0. 1931920790704947, 8: 0. 24881035953707603, 9: 0. 13868390351302598, 10: 0. 336067959653752, 11: 0. 16407815738375933, 12: 0. 33838887484747293, 13: 0. 2871391639624871, 14: 0. 22848023925633135 18

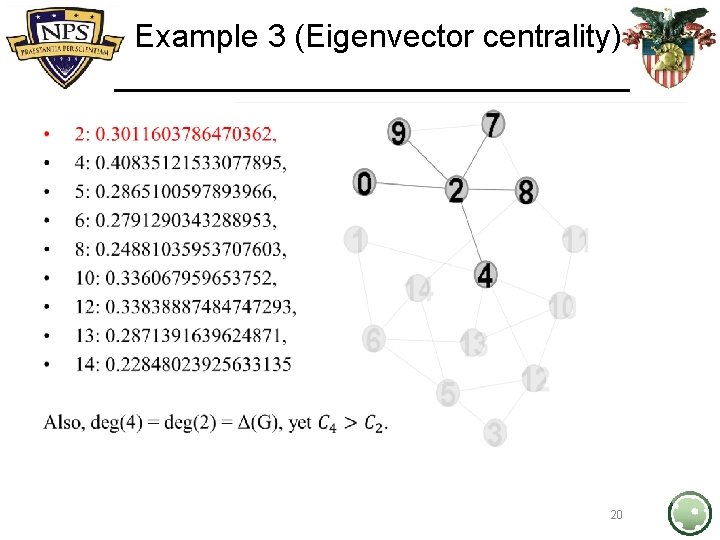
Example 3 (Eigenvector centrality) • • • 2: 0. 3011603786470362, 4: 0. 40835121533077895, 5: 0. 2865100597893966, 6: 0. 2791290343288953, 8: 0. 24881035953707603, 10: 0. 336067959653752, 12: 0. 33838887484747293, 13: 0. 2871391639624871, 14: 0. 22848023925633135 Also, deg(4) = deg(2) = Δ(G), yet… 19

Example 3 (Eigenvector centrality) • 20

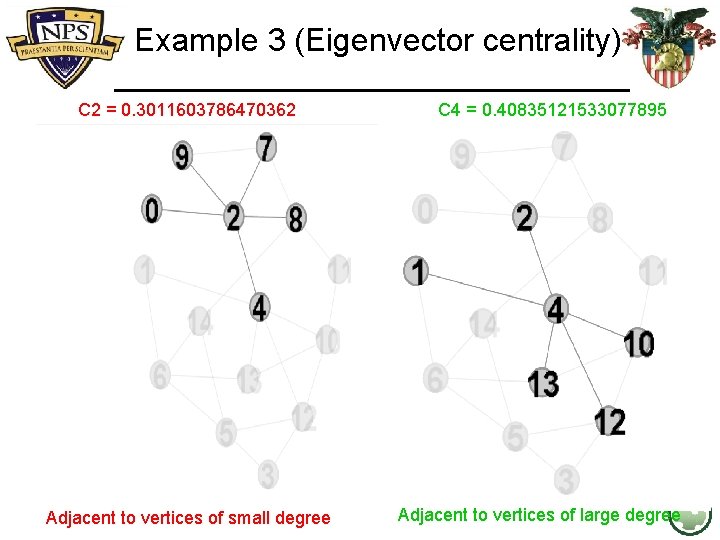
Example 3 (Eigenvector centrality) C 2 = 0. 3011603786470362 Adjacent to vertices of small degree C 4 = 0. 40835121533077895 Adjacent to vertices of large degree

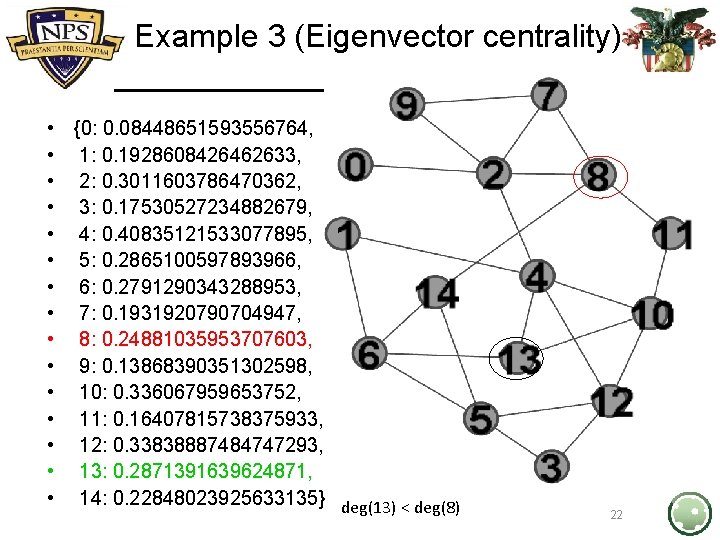
Example 3 (Eigenvector centrality) • • • • {0: 0. 08448651593556764, 1: 0. 1928608426462633, 2: 0. 3011603786470362, 3: 0. 17530527234882679, 4: 0. 40835121533077895, 5: 0. 2865100597893966, 6: 0. 2791290343288953, 7: 0. 1931920790704947, 8: 0. 24881035953707603, 9: 0. 13868390351302598, 10: 0. 336067959653752, 11: 0. 16407815738375933, 12: 0. 33838887484747293, 13: 0. 2871391639624871, 14: 0. 22848023925633135} deg(13) < deg(8) 22

Example 3 (Eigenvector centrality) • • • • {0: 0. 08448651593556764, 1: 0. 1928608426462633, 2: 0. 3011603786470362, 3: 0. 17530527234882679, 4: 0. 40835121533077895, 5: 0. 2865100597893966, 6: 0. 2791290343288953, 7: 0. 1931920790704947, 8: 0. 24881035953707603, 9: 0. 13868390351302598, 10: 0. 336067959653752, 11: 0. 16407815738375933, 12: 0. 33838887484747293, 13: 0. 2871391639624871, 14: 0. 22848023925633135} 23

Eigenvector Centrality • 24

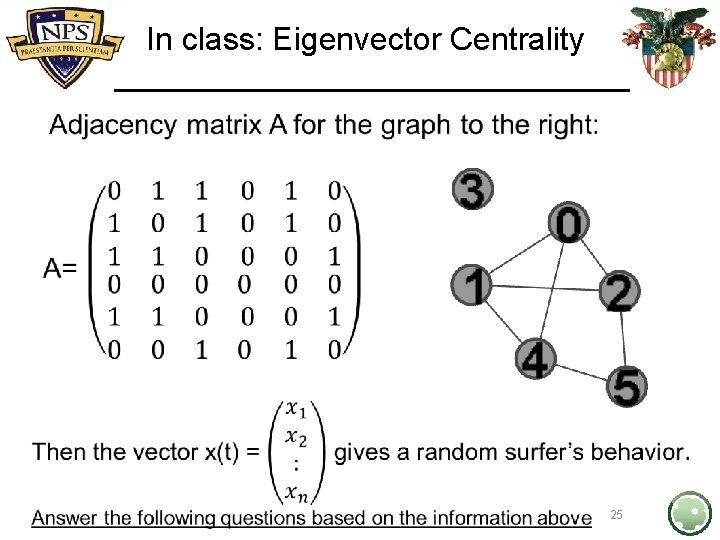
In class: Eigenvector Centrality • 25

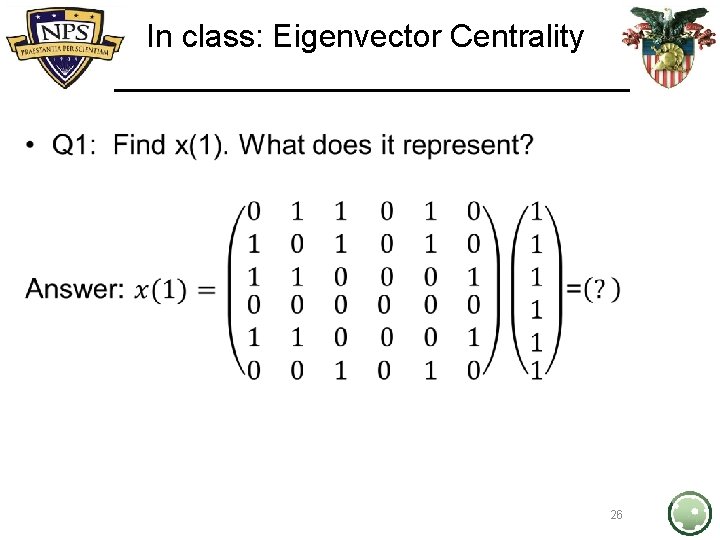
In class: Eigenvector Centrality • 26

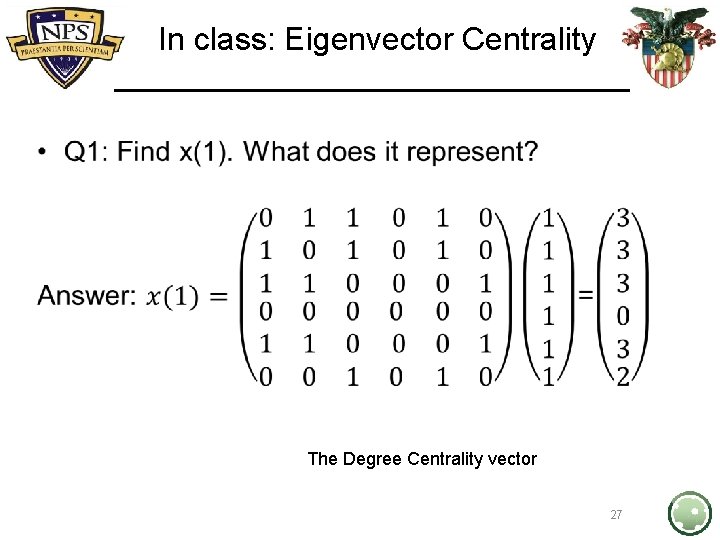
In class: Eigenvector Centrality • The Degree Centrality vector 27

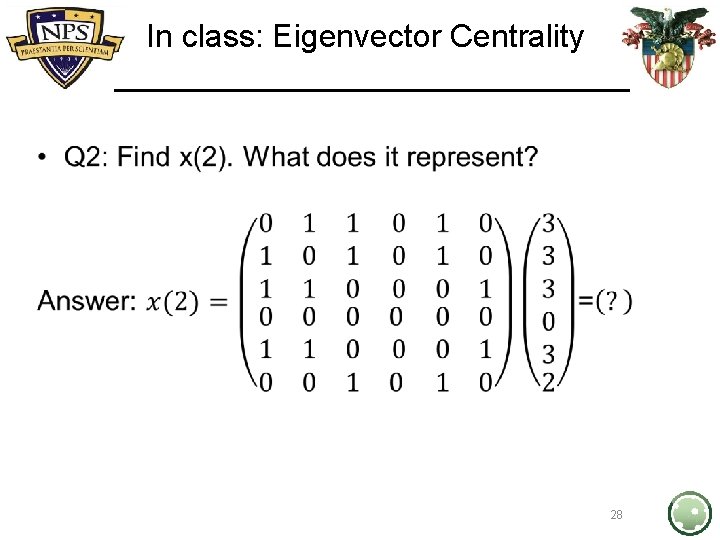
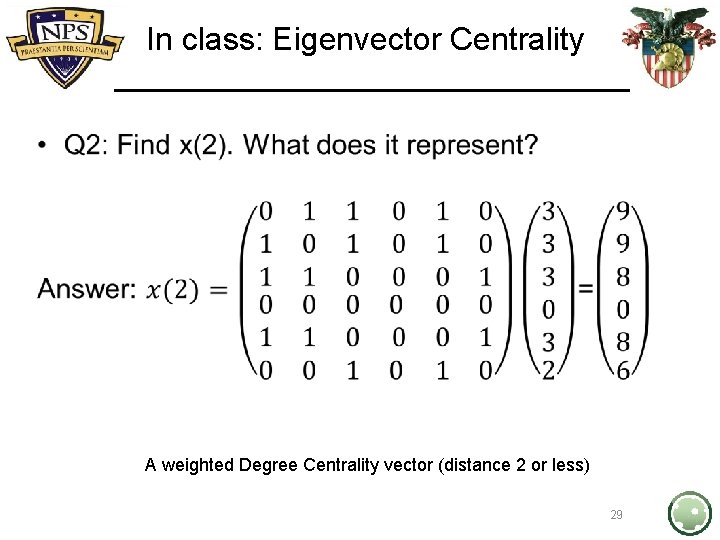
In class: Eigenvector Centrality • 28

In class: Eigenvector Centrality • A weighted Degree Centrality vector (distance 2 or less) 29

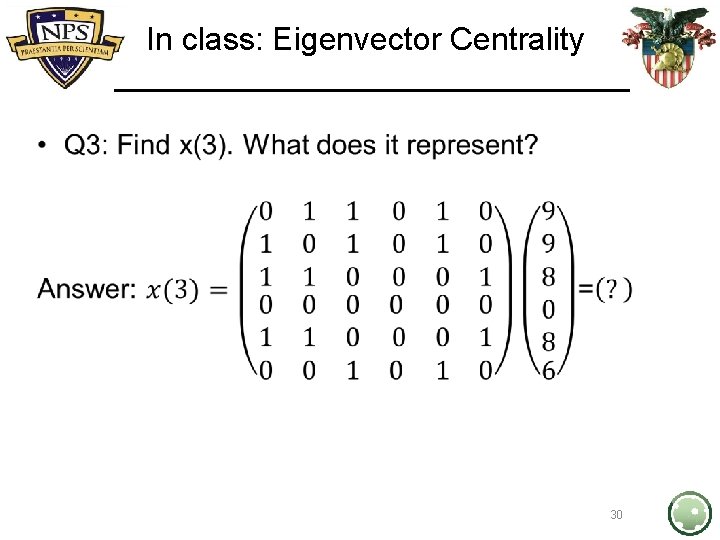
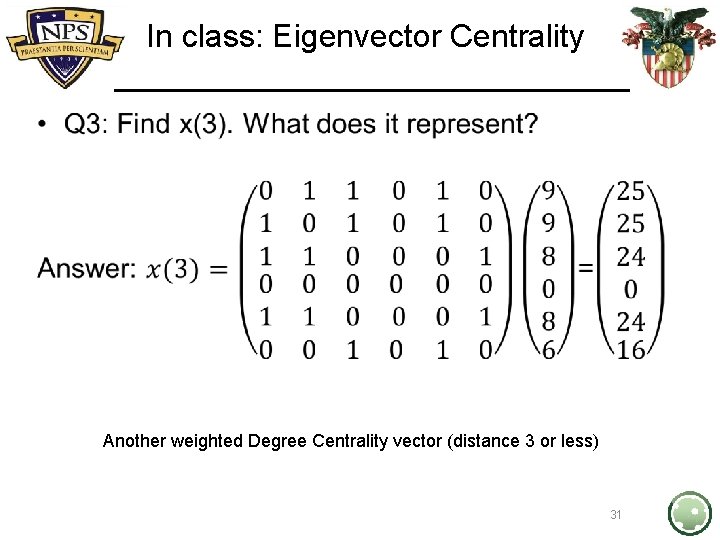
In class: Eigenvector Centrality • 30

In class: Eigenvector Centrality • Another weighted Degree Centrality vector (distance 3 or less) 31

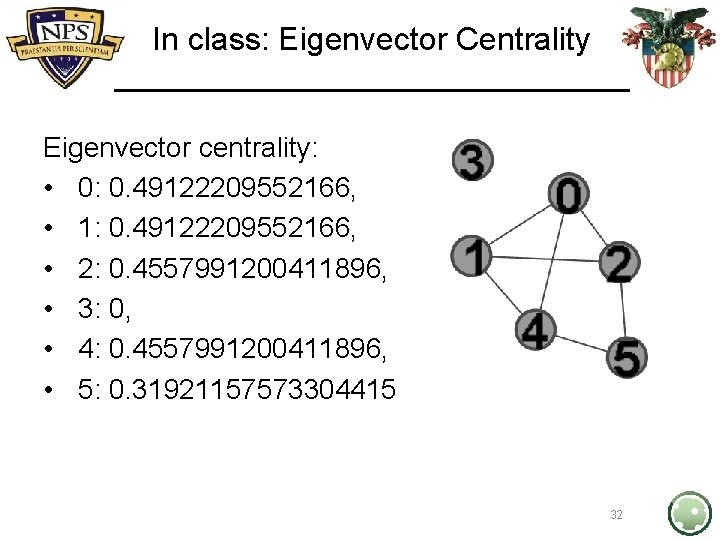
In class: Eigenvector Centrality Eigenvector centrality: • 0: 0. 49122209552166, • 1: 0. 49122209552166, • 2: 0. 4557991200411896, • 3: 0, • 4: 0. 4557991200411896, • 5: 0. 31921157573304415 32

Discussion: What did you notice? • 33

Discussion: Can you generalize it? • 34

Eigenvector Centrality Derivation •

Eigenvector Centrality Derivation •

Eigenvector Centrality • 37

Is it well defined? • That is: Is the vector guaranteed to exist? Is it unique? Is the eigenvalue unique? Can we have negative entries in the eigenvector? • We say that a matrix/vector is positive if all of its entries are positive • Perron-Frobenius theorem: A real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components • Perron-Frobenius theorem applies to positive matrices (but it gives similar information for nonnegative ones) 38

Perron-Frobenius theorem for nonnegative symmetric (0, 1)-matrices •

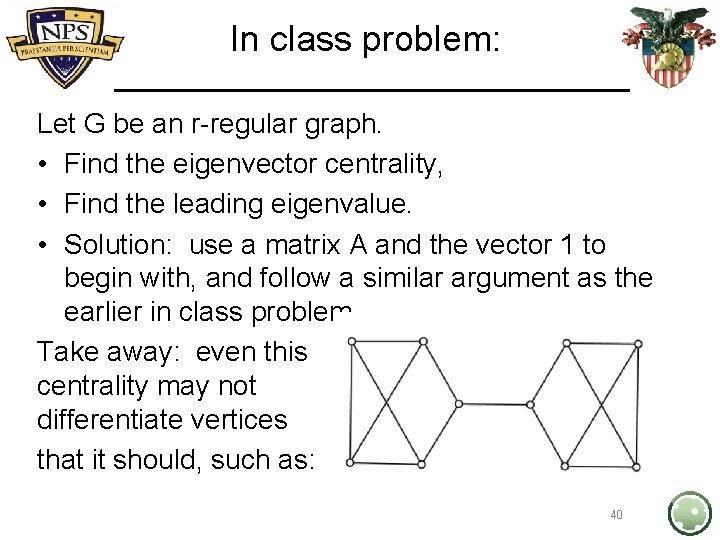
In class problem: Let G be an r-regular graph. • Find the eigenvector centrality, • Find the leading eigenvalue. • Solution: use a matrix A and the vector 1 to begin with, and follow a similar argument as the earlier in class problem Take away: even this centrality may not differentiate vertices that it should, such as: 40

In class problem (2) • 41

Eigenvector Centrality • 42