Riemannsommen De oppervlakte van het vlakdeel V in


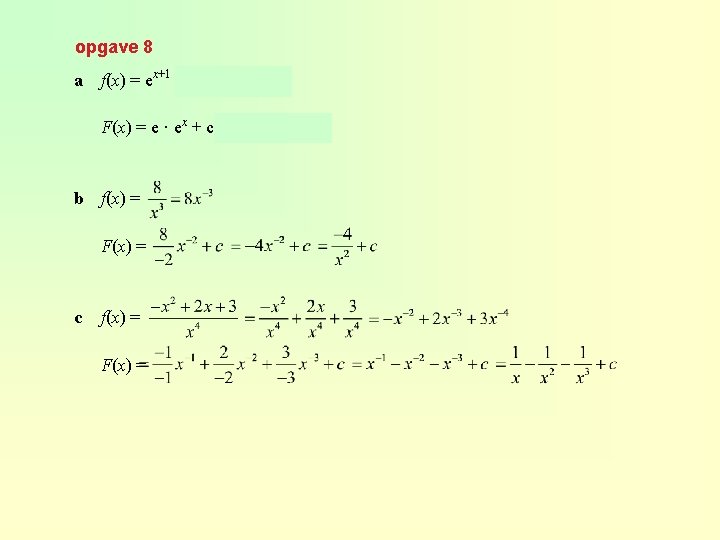
![Opgave f(x) = sin(x) met Df = [0, π] Voer in y 1 = Opgave f(x) = sin(x) met Df = [0, π] Voer in y 1 =](https://slidetodoc.com/presentation_image_h2/40200e4d2fd87e57f37634484d97fd8e/image-9.jpg)





- Slides: 19

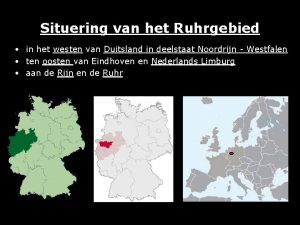
Riemannsommen De oppervlakte van het vlakdeel V in figuur a is te benaderen met behulp van rechthoeken. Daartoe verdeel je het interval [1, 5] in even lange deelintervallen. Hiernaast is gekozen voor rechthoeken met lengte ∆x = 1. Voor de hoogte van de rechthoeken kun je • de kleinste functiewaarde op het deelinterval nemen, je krijgt dan de ondersom, zie figuur b • de grootste functiewaarde op het deelinterval nemen, je krijgt dan de bovensom, zie figuur c • de functiewaarde van een willekeurig getal xk van het deelinterval nemen, zie figuur d In het algemeen wordt de som van de oppervlakten van rechthoeken genoteerd als Dit heet een Riemannsom. Ook de ondersom en bovensom zijn Riemannsommen. Er geldt ondersom ≤ O(V) ≤ bovensom. 10. 1

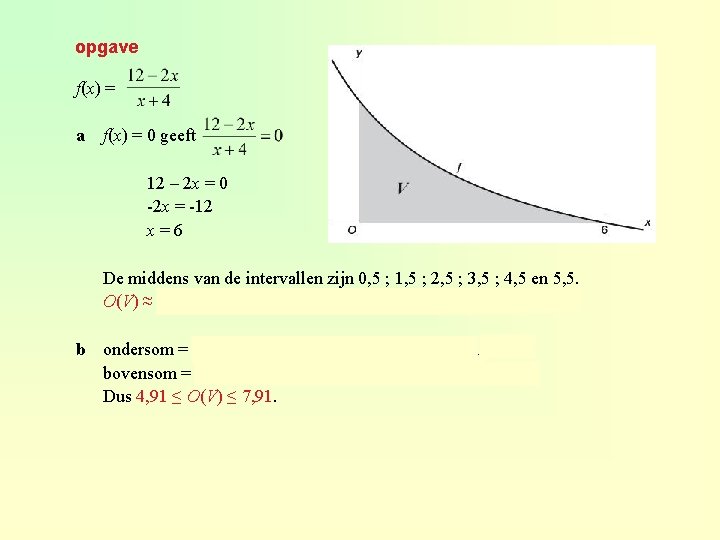
opgave f(x) = a f(x) = 0 geeft 12 – 2 x = 0 -2 x = -12 x=6 De middens van de intervallen zijn 0, 5 ; 1, 5 ; 2, 5 ; 3, 5 ; 4, 5 en 5, 5. O(V) ≈ (f(0, 5) + f(1, 5) + f(2, 5) + f(3, 5) + f(4, 5) + f(5, 5)) · 1 ≈ 6, 28 b ondersom = (f(1) + f(2) + f(3) + f(4) + f(5) + f(6)) · 1 ≈ 4, 91 bovensom = (f(0) + f(1) + f(2) + f(3) + f(4) + f(5)) · 1 ≈ 7, 91 Dus 4, 91 ≤ O(V) ≤ 7, 91.

Integralen Door bij een Riemannsom de limiet voor ∆x naar 0 te nemen krijg je een integraal. De oppervlakte van het vlakdeel V dat boven de x-as ligt en wordt ingesloten door de grafiek van f, de x-as en de lijnen x = a en x = b is Met de GR kun je integralen nauwkeurig benaderen. Zo is de oppervlakte van het vlakdeel V dat wordt ingesloten door de grafiek van f(x) = , de x-as en de y-as gelijk aan dx De optie fn. Int(TI) of ∫dx (Casio) geeft O(V) ≈ 1, 89. De oppervlakte van het vlakdeel W dat wordt ingesloten door de grafiek van f en de lijnen x = 2 en y = √ 2 bereken je met O(W) = O(rechthoek) – O(V). Dus O(W) ≈ 2 · √ 2 – 1, 89 ≈ 0, 94. 10. 1

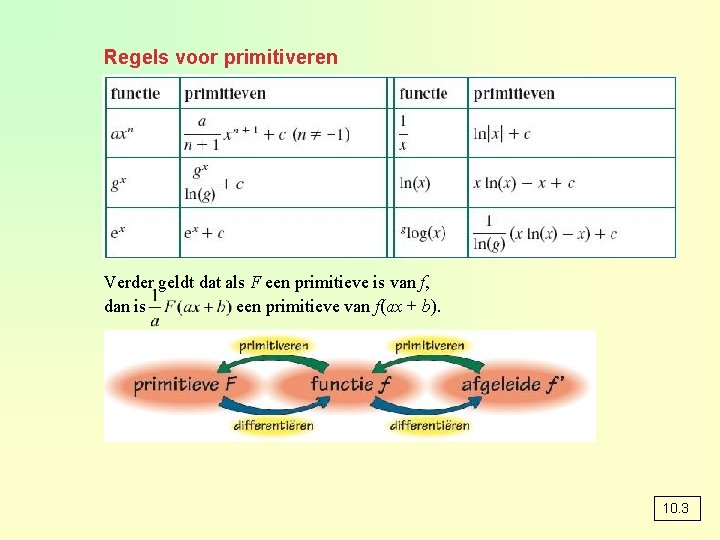
Regels voor primitiveren Verder geldt dat als F een primitieve is van f, dan is een primitieve van f(ax + b). 10. 3
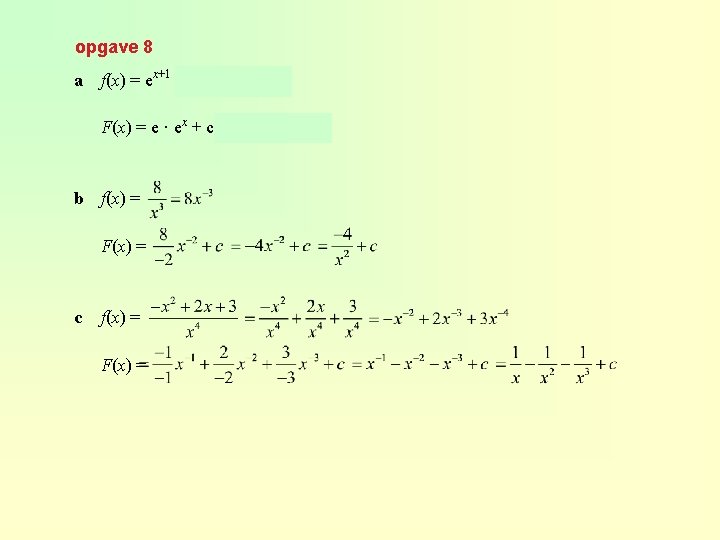
opgave 8 a f(x) = ex+1 = ex · e = e · ex F(x) = e · ex + c = ex+1 + c b f(x) = F(x) = c f(x) = F(x) =

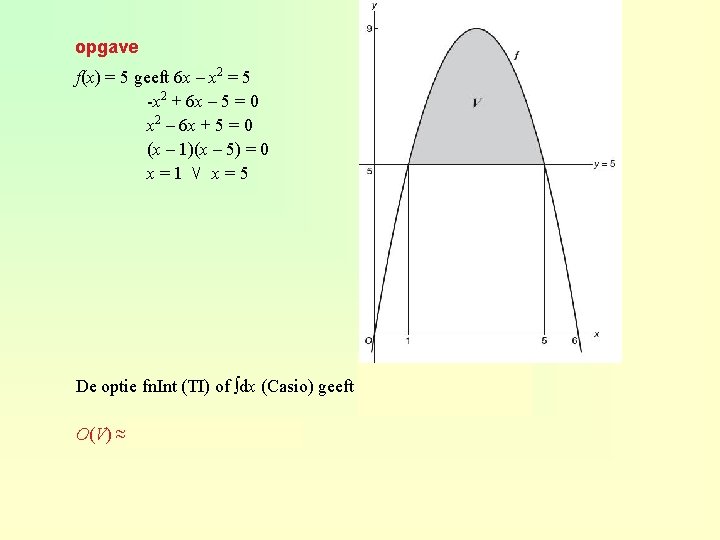
opgave f(x) = 5 geeft 6 x – x 2 = 5 -x 2 + 6 x – 5 = 0 x 2 – 6 x + 5 = 0 (x – 1)(x – 5) = 0 x=1 ⋁ x=5 De optie fn. Int (TI) of ∫dx (Casio) geeft O(V) ≈ 30, 667 – 4 · 5 ≈ 10, 67 ≈ 30, 667

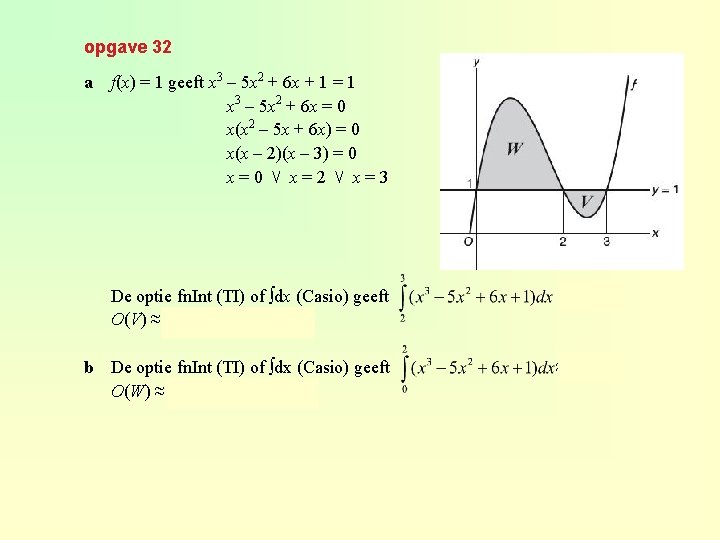
opgave 32 a f(x) = 1 geeft x 3 – 5 x 2 + 6 x + 1 = 1 x 3 – 5 x 2 + 6 x = 0 x(x 2 – 5 x + 6 x) = 0 x(x – 2)(x – 3) = 0 x=0 ⋁ x=2 ⋁ x=3 De optie fn. Int (TI) of ∫dx (Casio) geeft O(V) ≈ 1 · 1 – 0, 583 ≈ 0, 42 ≈ 0, 583. b De optie fn. Int (TI) of ∫dx (Casio) geeft O(W) ≈ 4, 667 – 2 · 1 ≈ 2, 67 ≈ 4, 667.

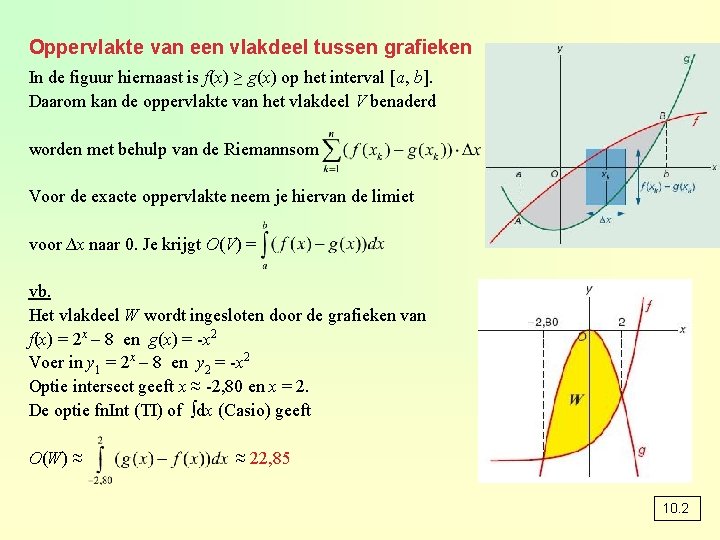
Oppervlakte van een vlakdeel tussen grafieken In de figuur hiernaast is f(x) ≥ g(x) op het interval [a, b]. Daarom kan de oppervlakte van het vlakdeel V benaderd worden met behulp van de Riemannsom Voor de exacte oppervlakte neem je hiervan de limiet voor ∆x naar 0. Je krijgt O(V) = vb. Het vlakdeel W wordt ingesloten door de grafieken van f(x) = 2 x – 8 en g(x) = -x 2 Voer in y 1 = 2 x – 8 en y 2 = -x 2 Optie intersect geeft x ≈ -2, 80 en x = 2. De optie fn. Int (TI) of ∫dx (Casio) geeft O(W) ≈ ≈ 22, 85 10. 2
![Opgave fx sinx met Df 0 π Voer in y 1 Opgave f(x) = sin(x) met Df = [0, π] Voer in y 1 =](https://slidetodoc.com/presentation_image_h2/40200e4d2fd87e57f37634484d97fd8e/image-9.jpg)
Opgave f(x) = sin(x) met Df = [0, π] Voer in y 1 = sin(x) en y 2 = ¼ x. De optie intersect geeft x ≈ 2, 4746. De optie fn. Int (TI) of ∫dx (Casio) geeft O(V) = en De lijn y = ¼ x verdeelt V niet in twee delen met gelijke oppervlakte.

Inhoud van een omwentelingslichaam Door het vlakdeel U in de figuur hiernaast te wentelen om de x-as ontstaat het lichaam L. I(L) = Door het vlakdeel V in de figuur hiernaast te wentelen om de x-as ontstaat het lichaam M. I(M) = vb. Het lichaam N ontstaat door het vlakdeel W, ingesloten door de grafieken van f(x) = 2 x – 8 en g(x) = -x 2 , te wentelen om de x-as. De optie fn. Int (TI) of ∫dx (Casio) geeft I(N) ≈ ≈ 593, 4 10. 2

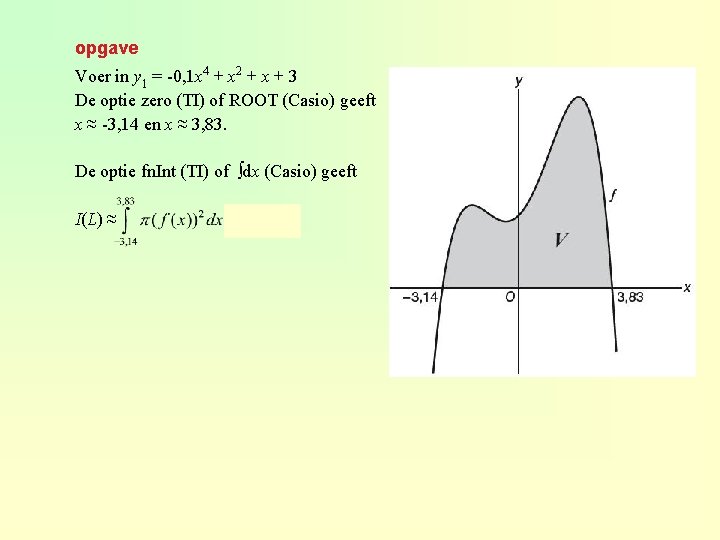
opgave Voer in y 1 = -0, 1 x 4 + x 2 + x + 3 De optie zero (TI) of ROOT (Casio) geeft x ≈ -3, 14 en x ≈ 3, 83. De optie fn. Int (TI) of ∫dx (Casio) geeft I(L) ≈

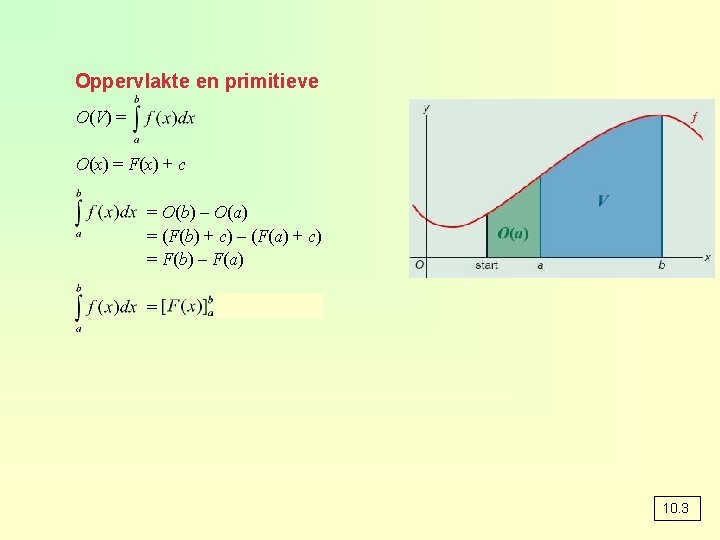
Oppervlakte en primitieve O(V) = O(x) = F(x) + c = O(b) – O(a) = (F(b) + c) – (F(a) + c) = F(b) – F(a) = = F(b) – F(a) 10. 3

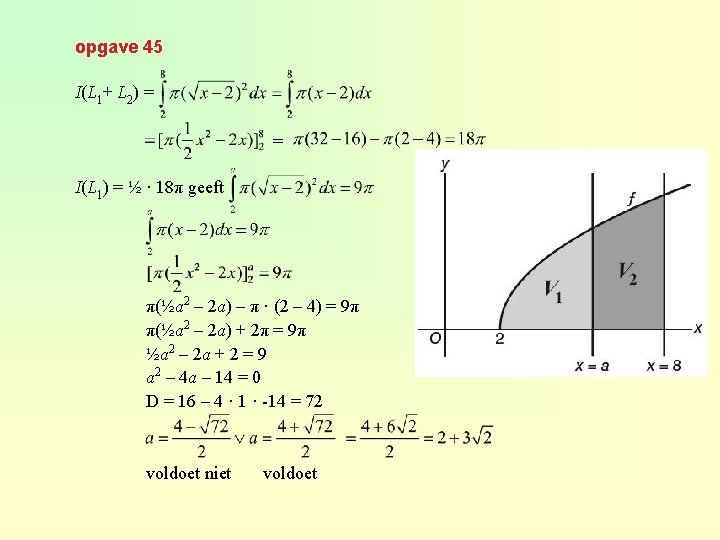
opgave 45 I(L 1+ L 2) = = I(L 1) = ½ · 18π geeft π(½a 2 – 2 a) – π · (2 – 4) = 9π π(½a 2 – 2 a) + 2π = 9π ½a 2 – 2 a + 2 = 9 a 2 – 4 a – 14 = 0 D = 16 – 4 · 1 · -14 = 72 voldoet niet voldoet

Wentelen om de y-as Het vlakdeel V ligt rechts van de y-as en wordt ingesloten door de grafiek van de functie f, de y-as en de lijnen y = a en y = b. De inhoud van het lichaam L dat ontstaat als V om de y-as wentelt is I(L) = 10. 4

Kegel en Bol Door het vlakdeel ingesloten door de lijn y = de x-as en de lijn x = h te wentelen om de x-as ontstaat een kegel met straal r en hoogte h. I(kegel) = ⅓πr 2 h Door de cirkel c: x 2 + y 2 = r 2 te wentelen om de x-as ontstaat een bol met straal r. I(bol) = 1⅓πr 3 Door het vlakdeel ingesloten door de cirkel c, de y-as en de lijn x = ⅔r te wentelen om de x-as ontstaat een bolschijf. I(bolschijf) = 10. 4

opgave 58

Booglengte De booglengte van het deel van de grafiek van een functie f tussen x = a en x = b is Bij de functie f(x) = krijg je de booglengte van het deel van de grafiek tussen x = 1 en x = 4 als volgt. f(x) = geeft booglengte = De optie fn. Int (TI) of ∫dx (Casio) geeft booglengte ≈ 3, 150. Dus de omtrek van het vlakdeel V in de figuur hiernaast is 3 + f(1) + f(4) + booglengte ≈ 7, 400. 10. 4

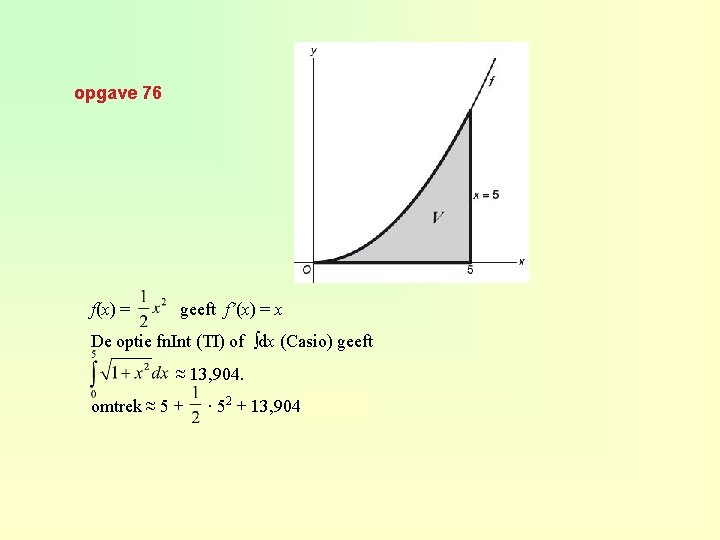
opgave 76 f(x) = geeft f’(x) = x De optie fn. Int (TI) of ∫dx (Casio) geeft ≈ 13, 904. omtrek ≈ 5 + · 52 + 13, 904 ≈ 31, 40

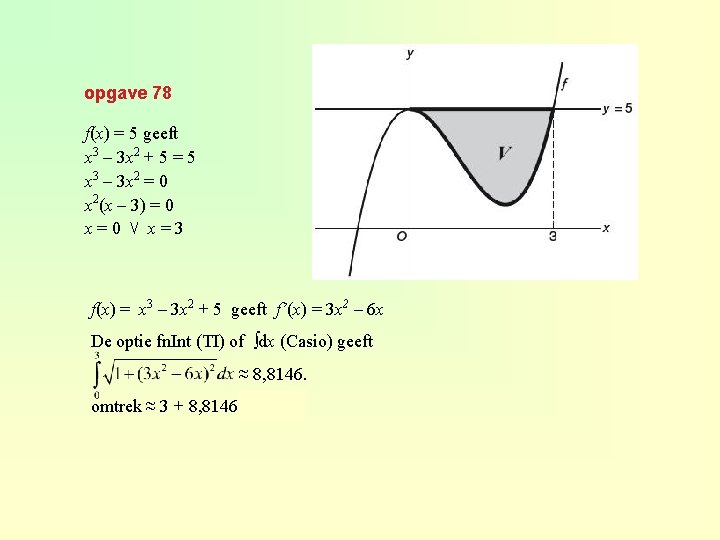
opgave 78 f(x) = 5 geeft x 3 – 3 x 2 + 5 = 5 x 3 – 3 x 2 = 0 x 2(x – 3) = 0 x=0 ⋁ x=3 f(x) = x 3 – 3 x 2 + 5 geeft f’(x) = 3 x 2 – 6 x De optie fn. Int (TI) of ∫dx (Casio) geeft ≈ 8, 8146. omtrek ≈ 3 + 8, 8146 ≈ 11, 81
 Zijn het heupbeen en het dijbeen van de walvis rudimenten?
Zijn het heupbeen en het dijbeen van de walvis rudimenten? Feodaal
Feodaal Stadia levenscyclus koolwitje
Stadia levenscyclus koolwitje Het stokske van johan van oldenbarnevelt
Het stokske van johan van oldenbarnevelt Het bloed stroomt waar het niet gaan kan
Het bloed stroomt waar het niet gaan kan Smout hespe en spek tekst
Smout hespe en spek tekst Uit het oog uit het hart frans
Uit het oog uit het hart frans Aartsvaders stamboom
Aartsvaders stamboom Regenead
Regenead Lengte grootheid
Lengte grootheid Oppervlakte omrekenen
Oppervlakte omrekenen Lengte oppervlakte inhoud
Lengte oppervlakte inhoud Trapezium pythagoras
Trapezium pythagoras Oppervlakte en dieptestructuur
Oppervlakte en dieptestructuur Spaanhoek wighoek vrijloophoek
Spaanhoek wighoek vrijloophoek Omtrek van n sirkel calculator
Omtrek van n sirkel calculator Metriek stelsel ha
Metriek stelsel ha Oppervlakte ruimtefiguren
Oppervlakte ruimtefiguren Oppervlakte zwembad berekenen
Oppervlakte zwembad berekenen De trein van het leven
De trein van het leven