Rekurzi 1 Szlvi Pter ELTE Informatika Szakmdszertani Csoport

Rekurzió 1. Szlávi Péter ELTE Informatika Szakmódszertani Csoport szlavi@ludens. elte. hu http: //izzo. inf. elte. hu/~szlavi 2000 Rekurzió 1

Tartalom 0 Bevezetés 0. 1 A rekurzió lényege; „klasszikus” példák 0. 2 A rekurzió helye a programkészítés folyamatában 1 Rekurzív specifikáció 1. 1 Formalizmus 1. 2 Példák 2 Rekurzív specifikáció és rekurzív algoritmus 3 Rekurzió megvalósítása nem rekurzív környezetben 3. 1 Problémák 3. 2 Példák 3. 3 A valódi megoldás ötlete, avagy mit tesz egy fordítóprogram? 2021. 05. 20. Rekurzió 1 2

Tartalom 4 Rekurzió és iteráció 4. 1 Oda 4. 2 Vissza 5 Rekurzív típusok 5. 1 Nevezetes rekurzív adatszerkezetek 5. 2 Rekurzív adatszerkezetek megadása 5. 3 A struktúrabejárás mint a feldolgozás „kerete” 6 Rekurzív adattípusok: fák 6. 1 Bináris fák 6. 2 Nem bináris fák 6. 3 B-fák 2021. 05. 20. Rekurzió 1 3

0 Bevezetés 0. 1 A rekurzió lényege; „klasszikus” példák Lényeg: „önhivatkozás” Például: Közismert hatékonysági gondok: Előzetes magyarázat: a rekurzió „szervezkedési” többletà lassúság tevékenysége (vermelések) à nagy helyfoglalás „Klasszikusok”: à faktoriális számok à Fibonacci-számok* 2021. 05. 20. Rekurzió 1 4

0 Bevezetés (folytatás) à Ackermann-függvény* : Elvadultságáról: • Ack(0, m)=m+1 • Ack(1, m)=m+2 • Ack(2, m)=2*m+3 • Ack(3, m)=2 m+3 -3 • Ack(4, m)= 2 -3, ahol az a 2 -t m+2 -ször tartalmazza kitevőként. à 2021. 05. 20. Binomiális számok: Rekurzió 1 5

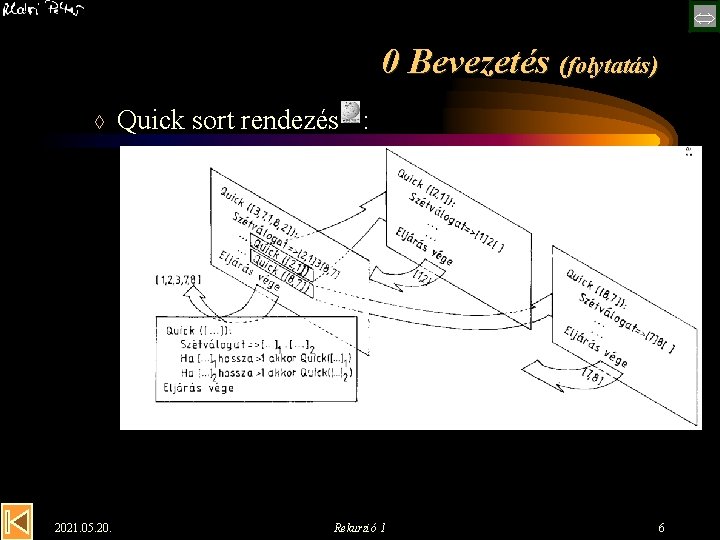
0 Bevezetés (folytatás) à 2021. 05. 20. Quick sort rendezés : Rekurzió 1 6

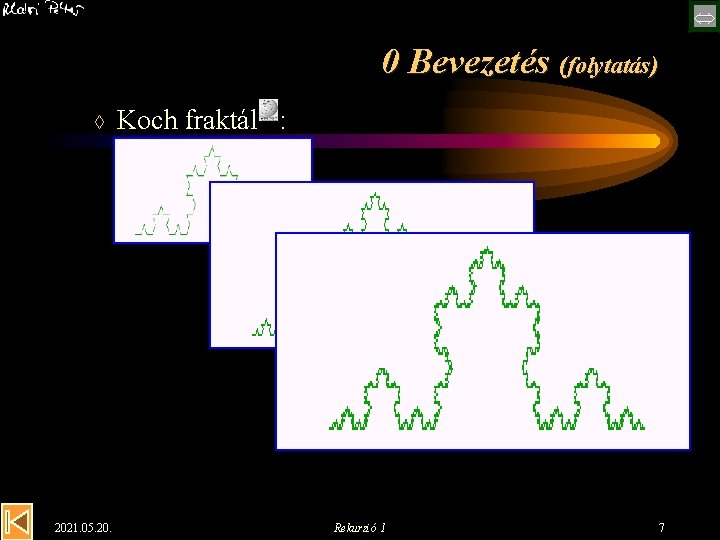
0 Bevezetés (folytatás) à 2021. 05. 20. Koch fraktál : Rekurzió 1 7

0 Bevezetés (folytatás) à 2021. 05. 20. Hanoi tornyai : Rekurzió 1 8

0 Bevezetés (folytatás) 0. 2 A rekurzió helye a programkészítés folyamatában: Rekurzív specifikáció Rekurzív algoritmus Rekurzív programkód Számítógép Nem rekurzív specifikáció Nem rekurzív algoritmus Nem rekurzív programkód Számítógép Megjegyzés: a rekurzió elvont értelemben általánosabb eszköz, mint az iteráció. [L. Mc. Carthy tétele, Paterson-Hewitt tétele a Manna: „Programozás elmélet” c. könyvben. ] 2021. 05. 20. Rekurzió 1 9

1 Rekurzív specifikáció 1. 1 Formalizmus(ról egy példán keresztül) Be: N N, X H* … Ki: Ef: Uf: Def: Y … N=Hossz(X). . . Nem rekurzív ág(ak) Y=Rek. Fv(X, N) Rek. Fv(x, n): H* N H* f(x, n) , ha T(x, n) Rek. Fv(x, n) : = g(Rek. Fv(x, n-1)) , egyébként Megállapodások: Rekurzív ág(ak) 1. Általában csak az utófeltételbeli definíciót adjuk meg a továbbiakban. 2021. 05. 20. Rekurzió 1 11

1 Rekurzív specifikáció (folytatás) 2. Az alábbi konstansok, függvények és operátorok definíció nélkül fölhasználhatók a rekurzív függvény definiálásakor: à à à 2021. 05. 20. ( _ ) – Üres sorozat Xi – az X sorozat i. eleme Hossz: H* N, Hossz((s 1, …, s. N)): =N Végére: H H* H*, Végére(x, (s 1, …, s. N)): =(s 1, …, s. N, x) Eleje: H* N H*, Eleje((s 1, …, s. N), i): =(s 1, …, si) Rekurzió 1 12

1 Rekurzív specifikáció (folytatás) 1. 2 Példák • Sorozatszámítás tétel • Eldöntés tétel • Kiválasztás tétel • Keresés tétel 2021. 05. 20. Rekurzió 1 13

1 Rekurzív specifikáció (folytatás) • Megszámolás tétel • Maximumkiválasztás tétel Hf: maximumérték kiválasztás • Másolás tétel • Kiválogatás tétel 2021. 05. 20. Rekurzió 1 14

1 Rekurzív specifikáció (folytatás) Megcseréli az X Maximum(X, n)-edik és n-edik elemét. Hf • Rendezés maximumkiválasztással L. előbb Figyelem: itt az n a sorozat még rendezendő részének utolsó elemének indexét jelöli; s csak kezdetben igaz: n=Hossz(X) • Szétválogatás tétel • Quick sort: 2021. 05. 20. hf Rekurzió 1 15

2 Rekurzív specifikáció és algoritmus Általánosságok: . . . emlékeztető a struktúra szerinti feldolgozás elvére, és alkalmazása a függvények világában… Példák: • Fibonacci-számok: Függvény Fib(Konstans N: Egész): Egész Elágazás N=0 esetén Fib: =0 N=1 esetén Fib: =1 egyéb esetben Fib: =Fib(N-1)+Fib(N-2) Elágazás vége Függvény vége. 2021. 05. 20. Rekurzió 1 16

2 Rekurzív specifikáció és algoritmus (folytatás) • Ackermann-függvény: Függvény Ack(Konstans N, M: Egész): Egész Elágazás N=0 esetén Ack: =M+1 N>0 és M=0 esetén Ack: =Ack(N-1, 1) egyéb esetben Ack: =Ack(N-1, Ack(N, M-1)) Elágazás vége Függvény vége. 2021. 05. 20. Rekurzió 1 18

2 Rekurzív specifikáció és algoritmus (folytatás) • Binomiális számok: Függvény B(Konstans N, K: Egész): Egész Ha K=0 vagy K=N akkor B: =1 különben B: =B(N-1, K)+B(N-1, K-1) Elágazás vége Függvény vége. A másik definíciójú algoritmus: hf. 2021. 05. 20. Rekurzió 1 19

2 Rekurzív specifikáció és algoritmus (folytatás) • „Quick sort” rendezés: Eljárás Quick(Változó A: TSorozat, Konstans E, V: Egész): [E, V az A “rendezendő” rész eleje, vége] Szétválogat(A, E, V, K) Ha K-E>1 akkor Quick(A, E, K-1) Ha V-K>1 akkor Quick(A, K+1, V) Eljárás vége. Meggondolandó: 1. a paraméterek eltérő hozzáférési joga; 2. a „Szétválogatás” eljárás; 3. milyen szélsőséges helyzetek adódnak hatékonyság szempontjából. 2021. 05. 20. Rekurzió 1 20

3 Rekurzió megvalósítása nem rekurzív környezetben 3. 1 Problémák „Állatorvosi ló (-: csacsi : -)” – a faktoriális függvény Fakt(Konstans N: Egész): Egész Változó f: Egész Ha N=0 akkor f: =1 különben f: =N*Fakt(N-1) Fakt: =f Függvény vége. Tételezzük föl, hogy a „környezet” képes az eljárások többszörös (értsd: egymásba ágyazott) hívásának lekezelésére. (Visszatérési cím a verembe; aktuális és formális paraméterek összekapcsolása. ) 2021. 05. 20. Rekurzió 1 21

3 Rekurzió megvalósítása nem rekurzív környezetben (folytatás) Milyen problémákkal szembesül a fordítóprogram, hogy a függvény végrehajtható legyen bármely N-re. Pl. ? Fakt(2)= 2 N [Ha 2=0 … különben] [Ha akkor 2=0 akkor … különben] N=0 f: =2* ? Fakt(2 -1)? 1 f: =N* ? Fakt(N-1)? Fakt: =f Fakt(1)= 1 N Fakt: =2 Fakt: =f [Ha akkor N=0 … különben] [Ha 1=0 akkor … különben] ? Fakt(N-1)? f: =1*f: =N* f: =1* 1 ? Fakt(1 -1)? Fakt: =f Fakt: =1 Fakt(0)= 0 N [Ha N=0 0=0 akkor] f: =1 Fakt: =f Fakt: =1 2021. 05. 20. Rekurzió 1 22

3 Rekurzió megvalósítása nem rekurzív környezetben (folytatás) Összefoglalva a problémákat: 1. A bemenő paraméter problematikája. Hogyan kerül a bemenő érték ugyanazzal a kóddal megvalósított eljáráshoz, azaz a rekurzívan újból a hívotthoz? 2. A függvényeljárások értékvisszaadása. Hogyan kerül a (rekurzívan) hívott függvény értéke a hívó eljárásban „felszínre”? 3. A lokális változók egyedisége. 2021. 05. 20. Rekurzió 1 23

3 Rekurzió megvalósítása nem rekurzív környezetben (folytatás) A megoldás vázlata: 1. és 3. probléma – belépéskor vermelés, kilépéskor veremből kivétel. 2. probléma (nem csak rekurziónál) – az érték verembe tétele közvetlenül a visszatérés előtt. A függvényt eljárássá alakítva (s az értékét verembe téve). Pl. Eljárás Fakt(Konstans N: Egész): Verembe(N) [paraméter a verembe] Ha N=0 akkor Fakt: =1 Csak az különben Fakt(N-1) [„függvény”-hívás] értékhez férés a cél. Veremből(f) [Fakt(N-1) értéke f] N: =Verem. Tető [az aktuális N] Fakt: =N*f [a függvényérték] Elágazás vége Veremből(N) [paraméter a veremből] Verembe(Fakt) [függvényérték a verembe] Eljárás vége. 2021. 05. 20. Rekurzió 1 24

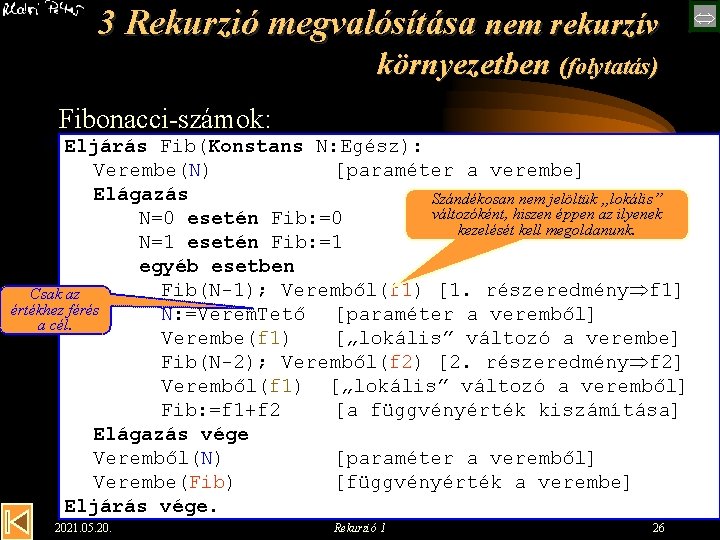
3 Rekurzió megvalósítása nem rekurzív környezetben (folytatás) Fibonacci-számok: Eljárás Fib(Konstans N: Egész): Verembe(N) [paraméter a verembe] Elágazás Szándékosan nem jelöltük „lokális” változóként, hiszen éppen az ilyenek N=0 esetén Fib: =0 kezelését kell megoldanunk. N=1 esetén Fib: =1 egyéb esetben Fib(N-1); Veremből(f 1) [1. részeredmény f 1] Csak az értékhez férés N: =Verem. Tető [paraméter a veremből] a cél. Verembe(f 1) [„lokális” változó a verembe] Fib(N-2); Veremből(f 2) [2. részeredmény f 2] Veremből(f 1) [„lokális” változó a veremből] Fib: =f 1+f 2 [a függvényérték kiszámítása] Elágazás vége Veremből(N) [paraméter a veremből] Verembe(Fib) [függvényérték a verembe] Eljárás vége. 2021. 05. 20. Rekurzió 1 26

3 Rekurzió megvalósítása nem rekurzív környezetben (folytatás) Binomiális számok: Eljárás B(Konstans N, K: Egész): Csak az N az és a K Verembe(N, K) értékéhez értékhezférésa cél. Ha K=0 vagy K=N akkor B: =1 különben B(N-1, K); Veremből(b 1) Veremből(K, N); Verembe(N, K) Verembe(b 1) B(N-1, K-1) Veremből(b 2); Veremből(b 1) B: =b 1+b 2 Elágazás vége Veremből(K, N) Verembe(B) [függvényérték a verembe] Eljárás vége. 2021. 05. 20. Rekurzió 1 27

3 Rekurzió megvalósítása nem rekurzív környezetben (folytatás) 3. 3 A valódi megoldás ötlete, avagy mit tesz egy fordítóprogram? A paraméterek számára a verembe helyet foglaló kódrészt generál. Pl. Eljárás QS(Változó x: T; à Konstans e, v: Egész; Változó k: Egész) esetén Aktuális paraméterek a QS(t, a, b, c) híváskor ilyesfélét: Verembe(Cím(t)) [Típustól függetlenül!] Verembe(a); Verembe(b); Verembe(Cím(c)) Formális paraméterek 2021. 05. 20. Rekurzió 1 28

3 Rekurzió megvalósítása nem rekurzív környezetben (folytatás) Az eljárástörzsben pedig a verem aktuális tetejéhez képesti relatív című hivatkozásokkal. Pl. Cím(x)=Verem. Tartalom(SP-|Cím(k)|-|v|-|e|-|Cím(x)|) à Cím(e)=SP-|Cím(k)|-|v|-|e| [bár a címe nem érhető el!] e=Verem. Tartalom(SP-|Cím(k)|-|v|-|e|). . . ahol a Verem. Tartalom annyi byte-nyi és olyan típusú értéket jelent, amely az adott adathoz tartozik; a |x| az x típusának megfelelő byte-szám. Pl. e=Verem. Tartalom(SP-|Cím(k)|-|v|-|e|) 2 byte-os egész számot jelent, hiszen e: Egész à Ugyanezeket kell megtenni a lokális adatokkal is. 2021. 05. 20. Rekurzió 1 29