Dinamikus programozs Szlvi Pter ELTE IK szlaviludens elte

Dinamikus programozás Szlávi Péter ELTE IK szlavi@ludens. elte. hu

Dinamikus programozás * tartalom 0 1 2 3 4 5 11/1/2020 Bevezetés Egy gondolatébresztő példa Első példázat * pénzváltás Második példázat * optimális pénzváltás Harmadik példázat * tükörszavak Irodalom Szlávi Péter: Dinamikus programozás 2/57

0 n 1. 2. 11/1/2020 Bevezetés A lényeg: Valamilyen probléma (optimális) megoldása úgy, hogy rekurzívan visszavezetjük rész problémák megoldására, de a rekurzió elkerülését (minimális ra szorítását) egy táblázat felépíté sével, és újrahasznosításával érjük el… Szlávi Péter: Dinamikus programozás 3/57

1 Egy gondolatébresztő példa 1. 1 Az „iskolapélda” – pénzfelválthatóság Bemenete: Bemenete P={p 1, . . . , p. N} pozitív egészek – a pénzcímletek, és E pozitív egész – a felváltandó összeg Kimenete: FelválthatóE logikai érték – jelentése = felváltható-e az E a P halmazban felsorolt cím letekkel úgy, hogy minden címletet legfeljebb egyszer használunk fel 11/1/2020 Szlávi Péter: Dinamikus programozás 4/57

1 Egy gondolatébresztő példa 1. 2 A példa „ízlelgetése” A felváltás „szerkezetének” elemzése Egy logikus rekurzív kapcsolat: Tfh. felváltható az E, ekkor (1 a) E = pi 1+…+pik , feltehető: (1 b) i 1<…<ik is. Ez esetben világos, hogy (2) E–pik = pi 1+…+pik 1 leírása az E–pik és {p 1, …, pik 1} paraméterek kel jellemzett redukált feladatnak 11/1/2020 Szlávi Péter: Dinamikus programozás 5/57

1 Egy gondolatébresztő példa Részproblémákra bontás A felhasználható címleteket rögzített sorrendűnek tekintve a {p 1, …, pi} hal mazt egyértelműen azonosíthatjuk i vel. Így bármely (rész)probléma azonosítható az (X, i) paraméter kettőssel, ahol X a felváltandó összeg és i a felváltáshoz felhasználható címletek utol sójának indexe A feladat: (E, N). A (2)-ben megfogal-mazott részfeladat: (E-pik, ik-1). 11/1/2020 Szlávi Péter: Dinamikus programozás 6/57

1 Egy gondolatébresztő példa Rekurzív összefüggések a részproblémák és megoldásaik között (vázlatosan) FV: N N L i. az éppen szükséges címlet FV(X, i) = Igaz, ha i. felhasználható és a mara 1. pi=X, vagy dék felváltható az előzőekkel 2. pi<X és FV(X pi, i 1), vagy 3. FV(X, i 1) i. nélkül, az előzőekkel felváltható 11/1/2020 Szlávi Péter: Dinamikus programozás 7/57

1 Egy gondolatébresztő példa Rekurzív megoldás egy lehetséges algoritmusa type TCimletek=record db: integer; cimlet: array [1. . Max. Cimlet. Db] of integer end; var Cimletek: TCimletek; function FV(const ìi > 0 Ù p = X Ú i ï FV(X, i) : = íi > 1 Ù pi < X Ù FV(X - p i , i - 1) Ú ïi > 1 Ù FV(X, i - 1) î 11/1/2020 X{felváltandó}, i{max. index}: integer): boolean; begin FV: =((i>0) and (Cimletek. cimlet[i]=X)) //i. éppen a kellő címlet or ((i>1) and FV(X, i 1)); //nem az, de i-1. -ig felváltható or ((i>1) and (Cimletek. cimlet[i]<X) and //i. felhasználható FV(X Cimletek. cimlet[i], i 1)) //és a maradék i-1. -ig felváltható end; //FV Szlávi Péter: Dinamikus programozás 8/57

1 Egy gondolatébresztő példa Próbák – elemzések: a) Kis címletszám (pl. {1, 2, 5}) mellett n n n b) „igenlő” a megoldás (pl. 8) – hívási sorrend „tagadó” a megoldás (pl. 9) – hívási sorrend mindkét végeredményhez olyan ada-tok alapján, amelyben van ismétlődő címlet – hívási sorrend, hívás-szám Különféle címletszám (pl. 5, 9, 15, …) mellett olyan összeg, amely azért nem váltható fel, mert túl nagy – hívás-szám növekedése Próbáljuk ki és következtessünk! Zip, exe 11/1/2020 Szlávi Péter: Dinamikus programozás 9/57

1 Egy gondolatébresztő példa a) tesztek … FV: =((i>0) and (Cimletek. cimlet [i]=X)) (Cimletek. cimlet[i]=X)) //i. éppen a kellő címlet or ((i>1) and FV(X, i 1)); //nem az, de i-1. -ig felváltható or ((i>1) and (Cimletek. cimlet [i]<X) and (Cimletek. cimlet[i]<X) //i. felhasználható FV(X Cimletek. cimlet[i], i 1)) FV( //és a maradék i-1. -ig felváltható … 11/1/2020 Szlávi Péter: Dinamikus programozás 10/57

1 Egy gondolatébresztő példa a) tesztek (folytatás) … FV: =((i>0) and (Cimletek. cimlet [i]=X)) (Cimletek. cimlet[i]=X)) //i. éppen a kellő címlet or ((i>1) and FV(X, i 1)); //nem az, de i-1. -ig felváltható or ((i>1) and (Cimletek. cimlet [i]<X) and (Cimletek. cimlet[i]<X) //i. felhasználható FV(X Cimletek. cimlet [i], i 1)) FV(X Cimletek. cimlet[i], i 1)) //és a maradék i-1. -ig felváltható … 11/1/2020 Szlávi Péter: Dinamikus programozás 11/57

1 Egy gondolatébresztő példa Tapasztalatok: A hívások módszeresen következnek egy-másután. Akár iterációval is „utánozhat-nánk”. (Legalábbis az ismétlésmentes esetben. ) l Az ismétlésmentes esetekben a hívás-szá-mok legfeljebb 1 értékűek, azaz legfeljebb egyszeres számolást jeleznek, ami a haté-konyság szempontjából megnyugtató. A 3. futásnál is még legfeljebb 2 az ismétlődő számítás, de a 4. -nél, ami alig különbözik a 3. -tól, már 4 helyen is „tripletet” látunk. S ez rosszat sejtet. l kód 11/1/2020 Szlávi Péter: Dinamikus programozás 12/57

1 l … FV: =((i>0) and (Cimletek. cimlet [i]=X)) (Cimletek. cimlet[i]=X)) //i. éppen a kellő címlet or ((i>1) and FV(X, i 1)); //nem az, de i-1. -ig felváltható or ((i>1) and (Cimletek. cimlet [i]<X) and (Cimletek. cimlet[i]<X) //i. felhasználható FV(X Cimletek. cimlet [i], i 1)) FV(X Cimletek. cimlet[i], i 1)) //és a maradék i-1. -ig felváltható … Egy gondolatébresztő példa A hívások során egy bináris fát „járunk be”. Pl. a „ 9 összeg {1, 2, 5} címletekkel” futáshoz tartozó bináris fa. kód 11/1/2020 Szlávi Péter: Dinamikus programozás 13/57

1 Egy gondolatébresztő példa b) tesztek 11/1/2020 Szlávi Péter: Dinamikus programozás 14/57

1 Egy gondolatébresztő példa Újabb tapasztalatok: Durván növekszik a hívás-szám (mindkét) paraméter növekedtével. l A legrosszabb (negatív végeredményű) esetekben a hívás-számokra „gyanús” értékeket kaptunk. Állítás: l Ha Rek. HDb(X, i) az X összeg felbonthatósá-gához szükségez rekurzív hívások számát jelenti (i. címlettel bezárólag), akkor legked-vezőtlenebb esetben a szükséges rekurzív hívások száma: Rek. HDb(X, i) = 2 i– 1 l 11/1/2020 A hívás-szám maximumát igenlő esetben is elérhetjük. Példát erre láss itt! Szlávi Péter: Dinamikus programozás 15/57

1 Röviden: DP. Egy gondolatébresztő példa A dinamikus programozásos megoldás Táblázatba gyűjtjük a részproblé mákra adott válaszokat. A táblázat sorai az egyes X összegek hez, oszlopai az egyes pi címletekhez rendeli az FV(X, i) értékeket. Éppúgy, ahogy az előbbi programnál tettünk, csakhogy ott tisztán adminisztratív, működés megértési céllal. A táblázatkitöltést a kis értékek felöl kezdjük: hiszen az FV(X, i) rekurzió jában FV(X, i– 1) és FV(X–pi, i– 1) szere pel. 11/1/2020 Szlávi Péter: Dinamikus programozás 16/57

1 Egy gondolatébresztő példa A megoldó kód vázlata: Az sg. Rek. Tab jelenti most a táblázatot: function Penz. Valtas_Din. Prog: boolean; begin Tablafeltoltes(Felvaltando, Cimletek. db); Penz. Valtas_Din. Prog: =sg. Rek. Tab. Cells[Cimletek. db+1, Felvaltando+2]='+'; end; 11/1/2020 Szlávi Péter: Dinamikus programozás 17/57

1 Egy gondolatébresztő példa procedure Tablafeltoltes (const E{felváltandó}, N{max. index}: integer); var i, x: integer; begin with fm. Penz. Valtas do begin for x: =1 to E do begin sg. Rek. Tab. Cells[2, x+2]: =' '; //első oszlop (=2 indexű) Hamis end; //for x //kivéve az 1. cimletnél: if Cimletek. cimlet[1]<=E then //van még cimlet[1]-dik sor? begin sg. Rek. Tab. Cells[2, Cimletek. cimlet[1]+2]: ='+'; end; //if … 11/1/2020 Szlávi Péter: Dinamikus programozás 18/57

… FV: =((i>0) and (Cimletek. cimlet [i]=X)) (Cimletek. cimlet[i]=X)) //i. éppen a kellő címlet or ((i>1) and FV(X, i 1)); //nem az, de i-1. -ig felváltható or ((i>1) and (Cimletek. cimlet [i]<X) and (Cimletek. cimlet[i]<X) //i. felhasználható FV(X Cimletek. cimlet [i], i 1)) FV(X Cimletek. cimlet[i], i 1)) //és a maradék i-1. -ig felváltható … … 1 Egy gondolatébresztő példa Rekurzív hívás helyett táblahasználat for i: =2 to N do//az i. oszlop számítása begin for x: =1 to E do begin if (Cimletek. cimlet[i]=x) or (sg. Rek. Tab. Cells[i, x+2]='+') or ((Cimletek. cimlet[i]<x) and (sg. Rek. Tab. Cells[i, x Cimletek. cimlet[i]+2]='+')) then sg. Rek. Tab. Cells[i+1, x+2]: ='+‘//igaz else sg. Rek. Tab. Cells[i+1, x+2]: =' '//hamis {end. If}; end; //for x end; //for i end; //with end; //Tablafeltoltes 11/1/2020 Szlávi Péter: Dinamikus programozás kód 19/57

1 Egy gondolatébresztő példa Összehasonlító futás: Próbáljuk ki és következtessünk! Zip, exe 11/1/2020 Szlávi Péter: Dinamikus programozás 20/57

1 Egy gondolatébresztő példa Megjegyzések: n n 11/1/2020 A rekurzív megoldás fajlagos ismétlési száma: 1 048 575 / 25 267 41. A DP 222 220 darab táblaelemet szá-mol ki, de csak egyszer. A fajlagos sebesség növekedés: 1 048 575 / 222 220 4, 7. A „feleslegesen” kiszámolt táblaelem szám: (222 220 – 25 267) = 196 953 7, 8 szorosa a szükségesnek. Szlávi Péter: Dinamikus programozás 21/57

1 Egy gondolatébresztő példa Egy „okosabb” DP megoldás Ötlet: ötvözni a rekurzív megoldás célratörését, azaz „csak azt kiszámol-ni, amit muszáj” elvét a DP megoldás „mindent csak egyszer kiszámolni” elvével. Tehát a számítás logikája rekurzív marad, de mielőtt egy rekurzív hívást kezdeményeznénk, megnézzük, nem lett e már kiszámolva. 11/1/2020 Szlávi Péter: Dinamikus programozás 22/57

1 11/1/2020 Egy gondolatébresztő példa már ismert a '+' válasz function FV(const X, i: integer): boolean; begin if (fm. Penz. Valtas. sg. Rek. Tab. Cells[i+1, X+2]='+') then begin már ismert a ‘-' válasz FV: =true end else if (fm. Penz. Valtas. sg. Rek. Tab. Cells[i+1, X+2]=' ') then begin FV: =false end még nem ismert a válasz else begin FV: =((i>0) and (Cimletek. cimlet[i]=X)) or ((i>1) and FV(X, i 1)) or ((i>1) and (Cimletek. cimlet[i]<X) and FV(X Cimletek. cimlet[i], i 1)) end kód {endif}; end; //FV Szlávi Péter: Dinamikus programozás 23/57

1 Egy gondolatébresztő példa Összehasonlító futás: Próbáljuk ki és következtessünk! Zip, exe 11/1/2020 Szlávi Péter: Dinamikus programozás 24/57

1 Egy gondolatébresztő példa 1. 3 A DP módszerének váza 1. A megoldás szerkezetének tanulmányozása – részproblémákra bontás megsejtése 2. Részproblémákra és összetevőkre bontás 3. Részproblémák megoldásának kifejezése rekurzívan az összetevők megoldásaiból – részproblémák és paramétereik körvonala zása: a rekurzió előkészítése – formalizálás: függvény definíció 4. Részproblémák megoldásának kiszámítása – a táblaszámítás algoritmizálása 1. 2. 5. kiszámítási sorrend meghatározása: minden részprob léma minden összetevője előbb szerepeljen a felsorolás ban az „alulról felfelé” haladó számítás A megoldás előállítása a 4. lépésben előállított táblázat segítségével – a megoldás algoritmizálása 11/1/2020 Szlávi Péter: Dinamikus programozás 25/57

2 Első példázat – pénzváltás 2. 1 A feladat Bemenete: Bemenete P={p 1, . . . , p. N} pozitív egészek – a pénzcímletek, és E pozitív egész – a felváltandó összeg Kimenete: S P – a felváltásban szereplő pénzcímletek; az S halmazban felsorolt címleteket legfeljebb egyszer használhatjuk fel 11/1/2020 Szlávi Péter: Dinamikus programozás 26/57

2 Első példázat – pénzváltás 2. 2 A megoldás 2. 2. 1 A megoldás szerkezetének tanulmányozása Ua. mint korábban… 11/1/2020 Szlávi Péter: Dinamikus programozás 27/57

2 Első példázat – pénzváltás 2. 2. 2 Részproblémákra és összetevők-re bontás A részproblémák a korábbiakhoz hason lóan fogalmazhatók meg. Az FV(X, i) jelentése viszont más: a legnagyobb P-beli elem indexe, amely még előfordul az X felváltásában. Pl. : P={2, 4, 5} N=3; X=7, akkor S={2, 5} FV(7, 3)=3, mert p 3=5, FV(7 p 3, 3 1)=FV(7 5, 3 1)=1, mert p 1=2, FV(2 p 1, 1 1)=FV(2 2, 1 1)=FV(0, 0). 11/1/2020 Szlávi Péter: Dinamikus programozás 28/57

2 Első példázat – pénzváltás 2. 2. 3 Részproblémák megoldásának kifejezése Vegyük észre, hogy akkor N+1 az ered-mény, ha nincs megoldás, s o, ha már nem kell folytatni. 11/1/2020 Szlávi Péter: Dinamikus programozás 29/57

2 Első példázat – pénzváltás 2. 2. 4 Részproblémák megoldásának kiszámítása A FV definíciójából látszik: csökkenő pa raméterekhez nyúl vissza, így a táblaki-töltő számítás kis értékektől indulhat a nagyobbak felé… 11/1/2020 Szlávi Péter: Dinamikus programozás 30/57

2 Első példázat – pénzváltás 2. 2. 5 A megoldás előállítása A megoldás meghatározása most bonyodalmasabb, mint volt korábban: hiszen most egy indexet kapunk a függvény ér-tékeként (k 1=FV(E, N)). A táblá-zatból kiolvasható a következőé (k 2=FV(E–pk 1, k 1– 1)), majd az azt követőé éít. Amíg a fel-váltandó összegparaméter 0 -ra nem csökken. Rekurzív megoldás esetén persze ez a visszalépdelés is rekurzívan történne. 11/1/2020 Szlávi Péter: Dinamikus programozás 31/57

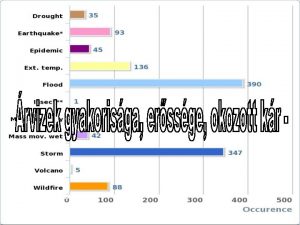
Az sg. Rek. Tab-ban az FVértékek; a Ki. Cimletek-ben képződik az eredmény 2 Első példázat – pénzváltás begin//Penz. Valtas_Din. Prog Tablafeltoltes(Felvaltando, Cimletek. db); Ki. Cimletek. db: =0; if str. To. Int(sg. Rek. Tab. Cells[Cimletek. db+1, Felvaltando+2])<= Cimletek. db then van megoldás: legbegin alább egy címlet k. X: =Felvaltando; k: =Cimletek. db; while k. X>0 do k. X felváltásához szükséges legnagyobb címlet indexe: k begin k: =str. To. Int(sg. Rek. Tab. Cells[k+1, k. X+2]); inc(Ki. Cimletek. db); Ki. Cimletek. cimlet[Ki. Cimletek. db]: =Cimletek. cimlet[k]; k. X: =k. X Cimletek. cimlet[k]; dec(k); k. X: a maradék összeg end; //while end; //if k. címlet már nem lehet, end; //Penz. Valtas_Din. Prog legfeljebb kisebb indexű 11/1/2020 Szlávi Péter: Dinamikus programozás 32/57

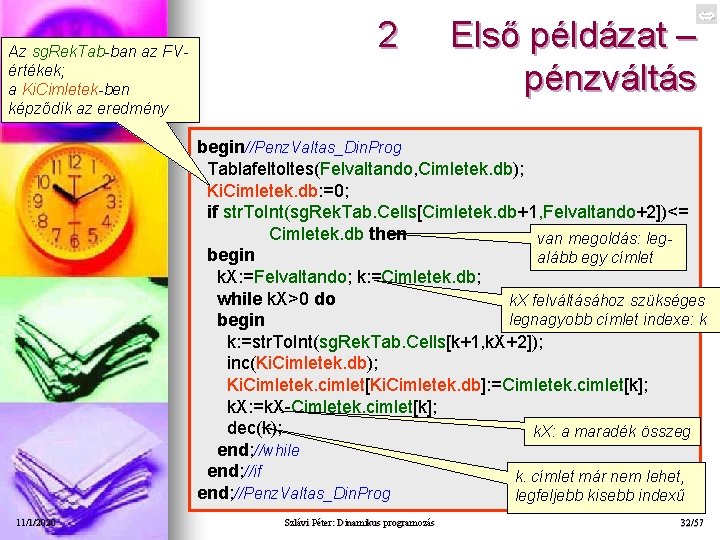
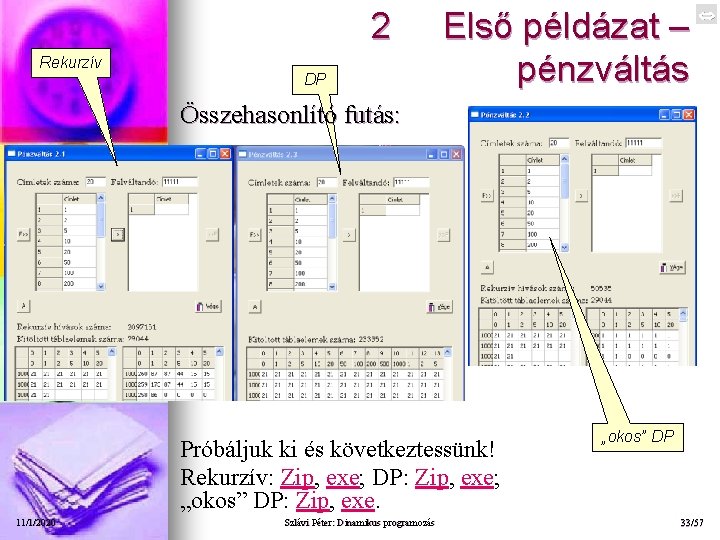
2 Rekurzív DP Első példázat – pénzváltás Összehasonlító futás: Próbáljuk ki és következtessünk! Rekurzív: Zip, exe; DP: Zip, exe; „okos” DP: Zip, exe. 11/1/2020 Szlávi Péter: Dinamikus programozás „okos” DP 33/57

3 Második példázat – optimális pénzváltás 3. 1 A feladat Bemenete: Bemenete P={p 1, . . . , p. N} pozitív egészek – a pénzcímletek, és E pozitív egész – a felváltandó összeg Kimenete: S P – a felváltásban szereplő pénzcímletek; az S halmazban felsorolt címleteket legfeljebb egyszer használhatjuk fel; S a lehető legkisebb elemszámú 11/1/2020 Szlávi Péter: Dinamikus programozás 34/57

3 Második példázat – optimális pénzváltás 3. 2 A megoldás … és nem lehetne „mohóskodni”… ? A problémánkhoz illeszkedő mohó választás: a még választhatók közül a legnagyobb címlet. Egy ellenpélda: P={5, 4, 4, 1, 1, 1} és E=8; a mohó megoldás: 8=5+1+1+1, ennél jobb: 8=4+4. 11/1/2020 Szlávi Péter: Dinamikus programozás 35/57

3 Második példázat – optimális pénzváltás 3. 2. 1 A megoldás szerkezetének tanulmányozása Ua. mint korábban… 11/1/2020 Szlávi Péter: Dinamikus programozás 36/57

3 Második példázat – optimális pénzváltás 3. 2. 2 Részproblémákra és összetevők-re bontás A részproblémák a korábbiakhoz hason lóan fogalmazhatók meg. Két lépésben oldjuk meg a feladatot. 1. Az Opt(X, i) jelentése: X felváltásához szükséges (első i közül választható) címletek száma. 2. Az FV(X, i) jelentése: a legnagyobb P beli elem indexe ( i), amely még elő fordul a X felváltásában. (Építünk az Opt ra. ) 11/1/2020 Szlávi Péter: Dinamikus programozás 37/57

3 Második példázat – optimális pénzváltás 3. 2. 3 Részproblémák megoldásának kifejezése Vegyük észre, hogy akkor N+1 az ered-mény, ha nincs megoldás; 0, ha célhoz értünk. 11/1/2020 Szlávi Péter: Dinamikus programozás 38/57

3 Második példázat – optimális pénzváltás Egy váratlan probléma: FV Opt A futás adminisztrálását végző táblapár nincs szinkron-ban. Bajt okoz, hogy a bal-felső tábla (1, 2) eleme üres. Pedig az alkalmazás foglalkozott vele, hiszen a bal-alsó tábla (1, 2) cellája helyesen 1 értéket tartalmaz. 11/1/2020 Szlávi Péter: Dinamikus programozás 39/57

3 Második példázat – optimális pénzváltás A probléma magyarázata: Az FV definíciójának optimumra hivatko zó rekurzív (3. ) ágánál tartunk, „készen kapja” a döntéséhez szükséges informá ciót. Ezért nem bontogatja le sem az (X–pi, i– 1), sem az (X, i– 1) részproblémákra; így a megoldás alapjául szolgáló, admi nisztratív táblázat ezen elemei kitöltet lenek maradnak; és a címleteket összeszedő részben katasz trófát okoz. 11/1/2020 Szlávi Péter: Dinamikus programozás 40/57

3 Második példázat – optimális pénzváltás A probléma megoldása: Az optimum kiszámításra többlet admi nisztrációt kell bízni: feljegyzi az FV hez tartozó táblázatba az általa e pil lanatban még ismert információt, hogy hányadik címlet szerepel a felbontás ban. 11/1/2020 Szlávi Péter: Dinamikus programozás 41/57

3 Második példázat – optimális pénzváltás 3. 2. 4 Részproblémák megoldásának kiszámítása A táblázatgenerálás sorrendje: A címletek szerint „alulról fölfelé” halad-va, de az érték szerint fordítva. A fordított irány magyarázatául: n az optimumot kiszámoló függvényhez tar-tozó táblázatot megspórolhatjuk (nincs szükség rá a végeredmény generálásához); n mivel csak az előző címlet oszlopára hivat-kozik, elegendő azt és az éppen számítás alatt állót megtartani, sőt n egyetlen oszlop is elegendő (lenne: -), ha a kiszámítás sorrendjét megfordítjuk. 11/1/2020 Szlávi Péter: Dinamikus programozás 42/57

3 Második példázat – optimális pénzváltás 3. 2. 5 A megoldás előállítása A megoldás meghatározása most az előző vel megegyező módon történik. 11/1/2020 Szlávi Péter: Dinamikus programozás 43/57

3 Második példázat – optimális pénzváltás az „okos” DP szokásos jelzője A puding próbája: Az alábbi táblázat összefoglalja a re kurzív és a memorizálós DP alkal mazás rekurzív hívásainak számát az {1, 2, 5, 10, 20, 50, 100, 200, 500, 1000, 1, 2, 5, 10, 20, 50, 100, 200, 500, 1000} címletek esetén: E FV 11/1/2020 FV + Opt Szlávi Péter: Dinamikus programozás 44/57

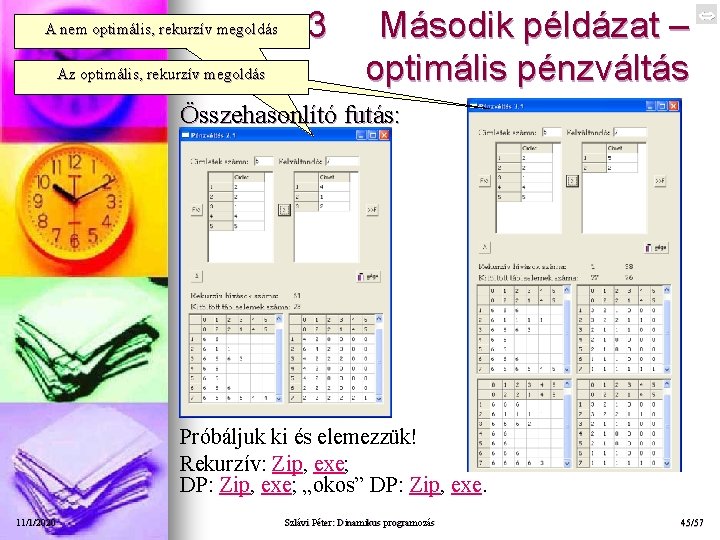
A nem optimális, rekurzív megoldás Az optimális, rekurzív megoldás 3 Második példázat – optimális pénzváltás Összehasonlító futás: Próbáljuk ki és elemezzük! Rekurzív: Zip, exe; DP: Zip, exe; „okos” DP: Zip, exe. 11/1/2020 Szlávi Péter: Dinamikus programozás 45/57

3 Második példázat – optimális pénzváltás Megjegyzések: n n 11/1/2020 Kitöltött táblaelemek száma kicsivel több, mint a nem optimális megoldást kereső esetében. (Mindkét táblát figyelem-be véve valamivel több, mint kétszerese. ) FV rekurzív hívások száma minimális. Az FVhez tartozó táblázat kitöltését döntően az Opt függvény végzi. A rekurzív hívások száma kisebb az optimumra nem törekvőénél. Sokkal kevésbé nő az össz rekurzív hívások száma az előbbinél. Szlávi Péter: Dinamikus programozás 46/57

4 Harmadik példázat – tükörszavak 4. 1 A feladat Bemenete: Bemenete szó={b 1, . . . , b. N} szó – jelek sorozata Kimenete: bj természetes szám – minimálisan ennyi jel beillesztésével tehető a szó palindrommá (tükörszóvá). 11/1/2020 Szlávi Péter: Dinamikus programozás 47/57

4 Harmadik példázat – tükörszavak 4. 2 A megoldás 4. 2. 1 A megoldás szerkezetének tanulmányozása TSz(S): az a szöveg, amely minimális számú jel beillesztésével képződik az S ből. Ilyen biztosan van: S&S’, ahol S’ az S megfordítása. 11/1/2020 Szlávi Péter: Dinamikus programozás 48/57

4 Harmadik példázat – tükörszavak Esetek: S= , akkor TSz(S)= =S. l Ha S egy jelből áll, akkor maga is tükörszó, azaz TSz(S)=S. l Legyen S=x&R&y, ahol x, y az S első és utolsó jele, és R akár üres is lehet. n Ha x=y, akkor TSz(S)=x&TSz(R)&y. … l Ha 11/1/2020 Szlávi Péter: Dinamikus programozás 49/57

4 Harmadik példázat – tükörszavak … n Ha x y, akkor TSz(S) első és utolsó jele vagy x vagy y. l Ha TSz(S)=x&U&x, ekkor x et szúr tunk be a végére, azaz U=TSz(R&y). l Ha TSz(S)=y&U&y, ekkor y t szúrtunk be az elejére, azaz U=TSz(x&R). Vagyis U gyanánt (ami eggyel rövidebb S nél) a TSz(R&y) és a TSz(x&R) közül azt kell választani, amely kevesebb beszúrással kapható meg. 11/1/2020 Szlávi Péter: Dinamikus programozás 50/57

4 Harmadik példázat – tükörszavak 4. 2. 2 Részproblémákra és összetevők-re bontás Jelölések: MSz(i, j) – a minimális jel beillesztések száma, és szó(i. . j) – a szó szöveg i. és j. jele kö zötti része szó(i): =szó(i. . i) – a szó i. jele. 11/1/2020 Szlávi Péter: Dinamikus programozás 51/57

4 Harmadik példázat – tükörszavak Kapcsolatok: n Ha i j, akkor nincs mit tenni. n Ha i<j és l szó(i)= szó(i) szó(j), akkor jel beillesztések számát az MSz(i+1, j– 1) részprobléma határozza meg. l szó(i) szó(j), akkor az MSz(i+1, j) és az MSz(i, j– 1) közül a kisebb értékűt kell választanunk. A kiinduló probléma e jelölésekkel: MSz(1, Hossz(szó)). 11/1/2020 Szlávi Péter: Dinamikus programozás 52/57

4 Harmadik példázat – tükörszavak 4. 2. 3 Részproblémák megoldásának kifejezése 11/1/2020 Szlávi Péter: Dinamikus programozás 53/57

4 Harmadik példázat – tükörszavak 4. 2. 4 Részproblémák megoldásának kiszámítása A táblázat generálás sorrendje: Az (i, j)-vel azonosított részprobléma az (i+1, j– 1), az (i+1, j) és az (i, j– 1) rész-problémáktól függ. Tehát a kiszámítási sorrend i-értelemben fogyó, j-értelem-ben növekvő lehet. Mivel a rekurzió során csak a közvetlen szomszédra van szükség ezért elegendő egyetlen oszlopot tárolni. 11/1/2020 Szlávi Péter: Dinamikus programozás 54/57

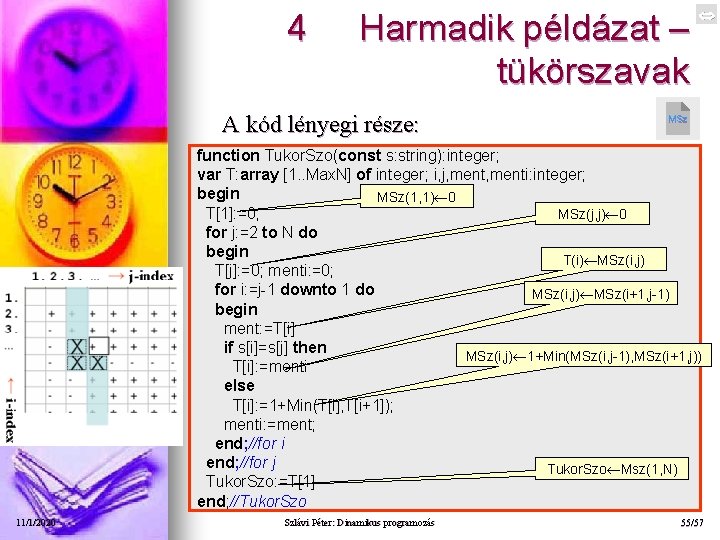
4 Harmadik példázat – tükörszavak A kód lényegi része: MSz function Tukor. Szo(const s: string): integer; var T: array [1. . Max. N] of integer; i, j, menti: integer; begin MSz(1, 1) 0 T[1]: =0; MSz(j, j) 0 for j: =2 to N do begin T(i) MSz(i, j) T[j]: =0; menti: =0; for i: =j 1 downto 1 do MSz(i, j) MSz(i+1, j 1) begin ment: =T[i] if s[i]=s[j] then MSz(i, j) 1+Min(MSz(i, j 1), MSz(i+1, j)) T[i]: =menti else T[i]: =1+Min(T[i], T[i+1]); menti: =ment; end; //for i end; //for j Tukor. Szo Msz(1, N) Tukor. Szo: =T[1] end; //Tukor. Szo 11/1/2020 Szlávi Péter: Dinamikus programozás 55/57

4 Harmadik példázat – tükörszavak 4. 2. 5 A megoldás előállítása … nem nagy kaland: a tábla (1, Hossz(szó)) eleme, amelyet az algoritmusbeli T vektor első eleme tartalmaz. 11/1/2020 Szlávi Péter: Dinamikus programozás 56/57

5 Irodalom [HGy] Horváth Gyula: „Tehetséggondozó Program – Dinamikus programozás”, NJSz. T, 2005 [RISz] Rónyai L. , Ivanyos G. , Szabó R. : Algoritmusok, TYPOTEX, 1999 [Sz. P] Szlávi Péter: „Dinamikus programozás”, kézirat http: //people. inf. elte. hu/szlavi/DP/ Dinamikus. Programozas. pdf [Sz. P 2] Szlávi Péter et al. : „További példák a dinamikus programozáshoz”, kézirat http: //people. inf. elte. hu/szlavi/ Pr. M 4 felev/Dina. Prog/ 11/1/2020 Szlávi Péter: Dinamikus programozás 57/57