Quantum Computing Lecture 22 Michele Mosca Correcting Phase

Quantum Computing Lecture 22 Michele Mosca

Correcting Phase Errors l Suppose the environment effects error on our quantum computer, where This is a description of errors in phase because we use powers of operator Z

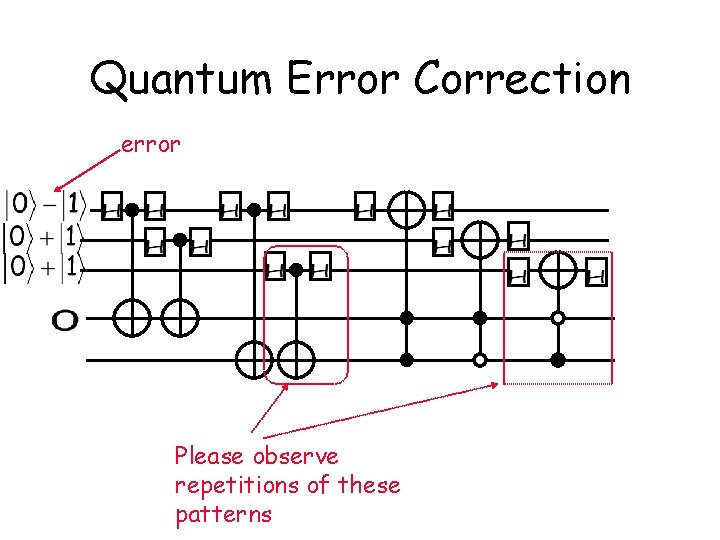
Quantum Error Correction l We can encode Z error in upper bit l Consider error term logical 0 gives acting on the Such error arriving in decoder is shown next slide

Quantum Error Correction error Please observe repetitions of these patterns

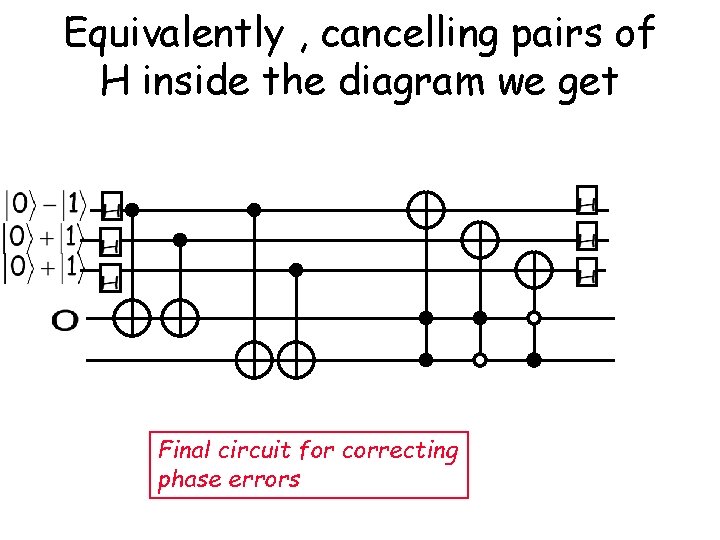
Equivalently , cancelling pairs of H inside the diagram we get Final circuit for correcting phase errors

Quantum Error Correction l If the error effected on the system in state is of the form

Quantum Error Correction l and if the state only consists of mixtures of superpositions of codewords and then the correction procedure (call it map ) will

Correcting both phase errors and bit flip errors l Consider the codewords of Shor’s code We can easily correct any single X- error in one of the 3 three-bit parts l We can then also correct a single Z- error on one of the 9 qubits. l This means we can also correct Y-errors on one of the 9 qubits l

Quantum Error Correction l Theorem 10. 2: Suppose C is a quantum code and is the error-correction operation constructed in the proof of Theorem 10. 1 to recover from a noise process with operation elements. Suppose is a quantum operation with elements which are linear combinations of the. Then the error correction operation also corrects the effects of the noise process on the code C.

Correcting any error Since any error operator Ek can be written as a linear combination of I, X, Z and Y, then the same procedure will correct ANY error acting on just 1 of the 9 qubits. l If where is a quantum operator whose operator terms are correctable with correction operator , then l

l Correcting any error Theorem 10. 1 (Quantum Error Correction Conditions) Let C be a quantum code, and let P be the projector onto C. Suppose is a quantum operation with operation elements A necessary and sufficient condition for the existence of an error-correction operation correcting on C is that for some Hermitian matrix numbers. l (no mention of efficiency) of complex

Degenerate Codes Consider the 9 -qubit code. l A single Z-error on the first qubit of a codeword produces the same outcome as a single Z-error on either the 2 nd or 3 rd qubit. l The correction procedure will correct these errors regardless l A degenerate code is one where two correctable errors produce the same effect on the codewords (this is impossible with classical codes). l

Quantum Hamming Bound l l Any non-degenerate quantum error correcting code that encodes k logical qubits into n qubits and can correct errors on up to t qubits must have If t=k=1, we get (there exists a 5 qubit code that accomplishes this)