Quantum Factoring Michele Mosca The Fifth Canadian Summer












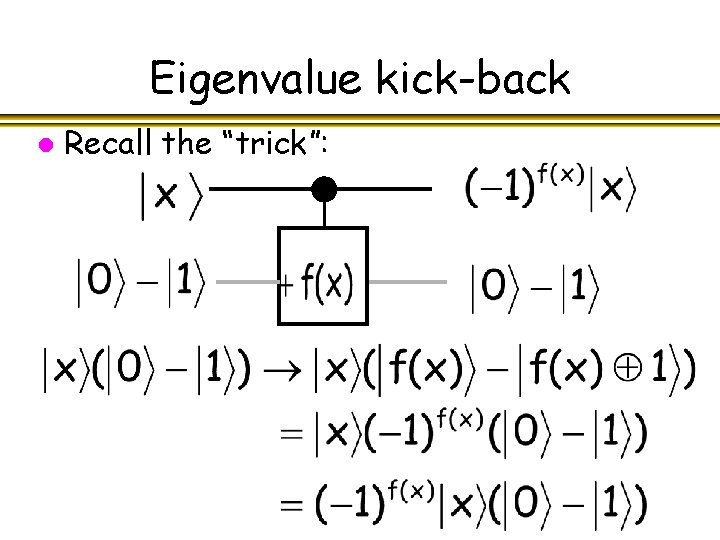








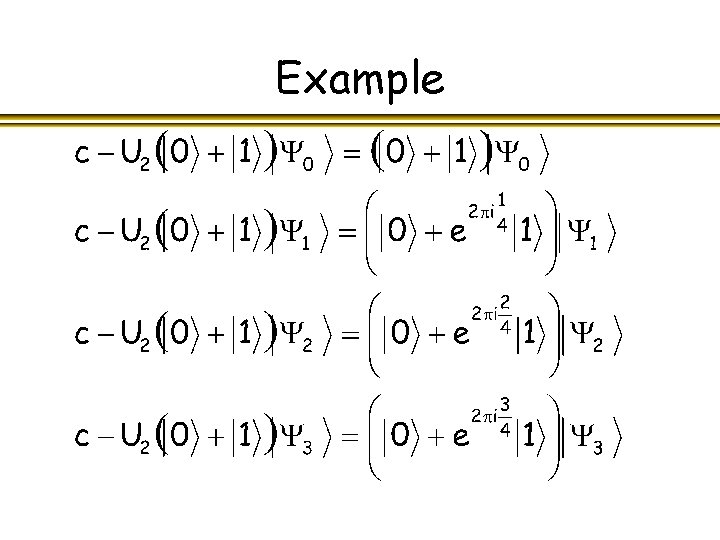















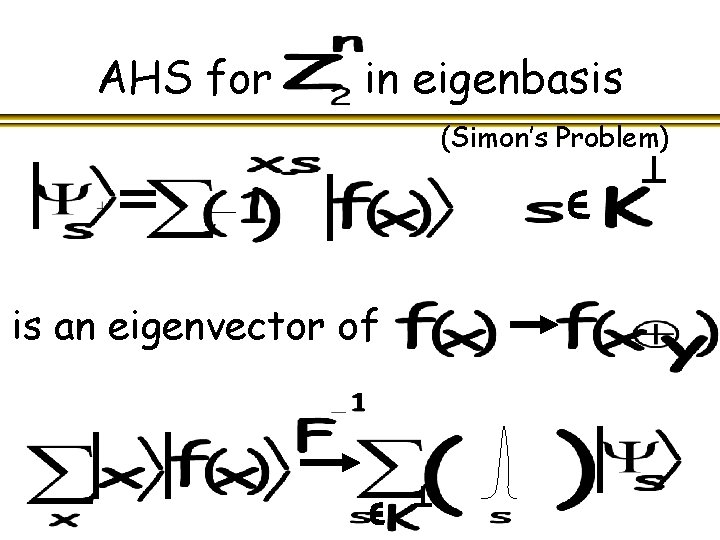


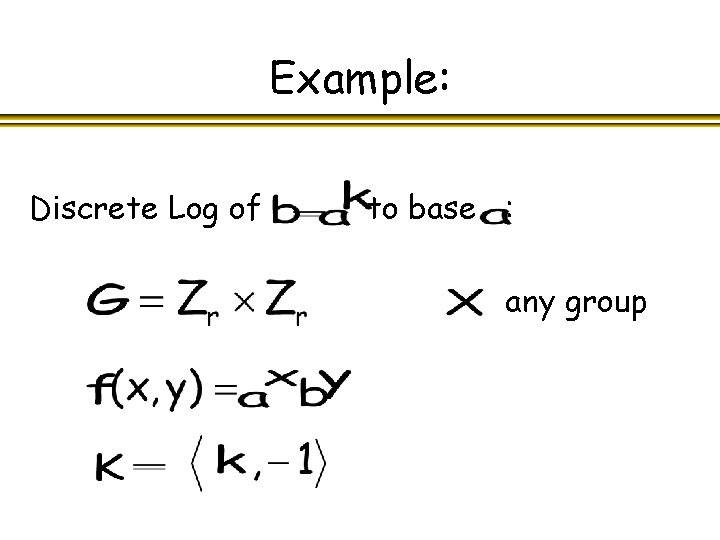




- Slides: 76

Quantum Factoring Michele Mosca The Fifth Canadian Summer School on Quantum Information August 3, 2005

Quantum Algorithms should exploit quantum parallelism and quantum interference. l We have already seen some elementary algorithms. l

Quantum Algorithms These algorithms have been computing essentially classical functions on quantum superpositions l This encoded information in the phases of the basis states: measuring basis states would provide little useful information l But a simple quantum transformation translated the phase information into information that was measurable in the computational basis l

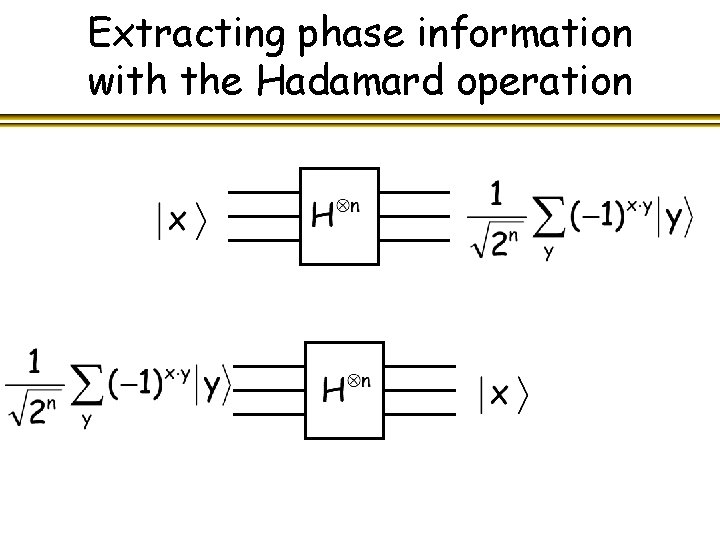
Extracting phase information with the Hadamard operation

Overview Quantum Phase Estimation l Eigenvalue Kick-back l Eigenvalue estimation and orderfinding/factoring l Shor’s approach l Discrete Logarithm and Hidden Subgroup Problem (if there’s time) l

Quantum Phase Estimation l Suppose we wish to estimate a number given the quantum state l Note that in binary we can express

Quantum Phase Estimation l Since for any integer k, we have

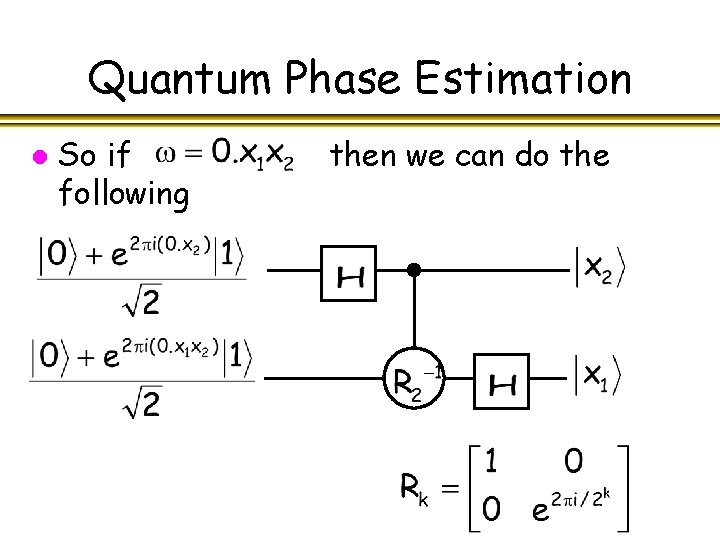
Quantum Phase Estimation l If then we can do the following

Useful identity l We can show that

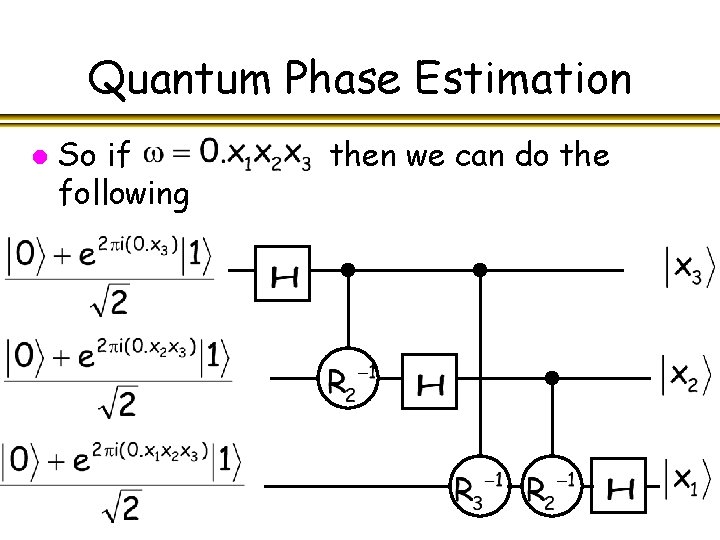
Quantum Phase Estimation l So if following then we can do the

Quantum Phase Estimation l So if following then we can do the

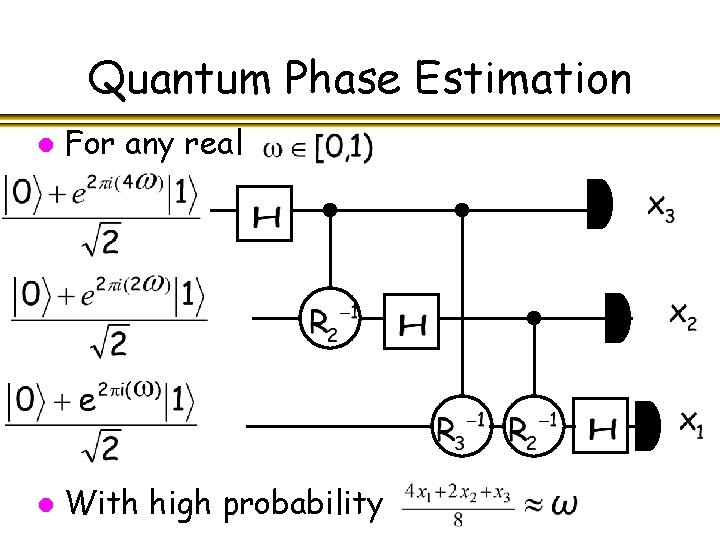
Quantum Phase Estimation l Generalizing this network (and reversing the order of the qubits at the end) gives us 2 a network with O(n ) gates that implements

Discrete Fourier Transform l l The discrete Fourier transform maps vectors of dimension N by transforming the elementary vector according to The quantum Fourier transform maps vectors in a Hilbert space of dimension N according to

Discrete Fourier Transform l Thus we have illustrated how to implement (the inverse of) the quantum Fourier n transform in a Hilbert space of dimension 2

Estimating arbitrary l l What if form is not necessarily of the for some integer x? The QFT will map superposition where to a

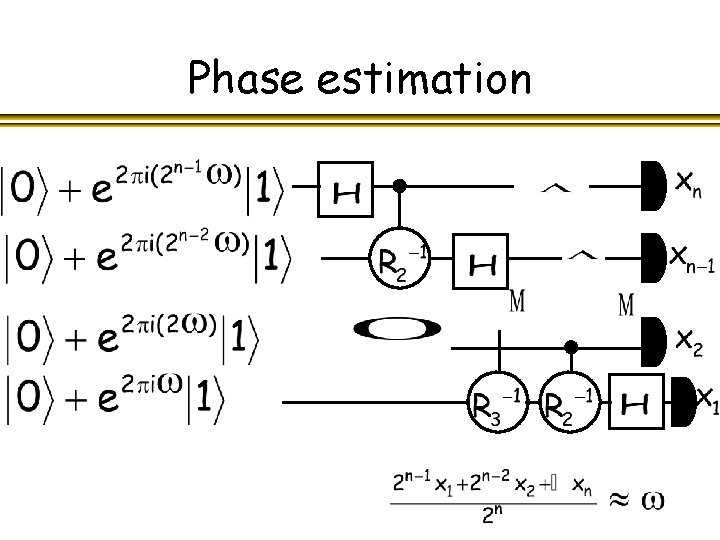
Quantum Phase Estimation l For any real l With high probability
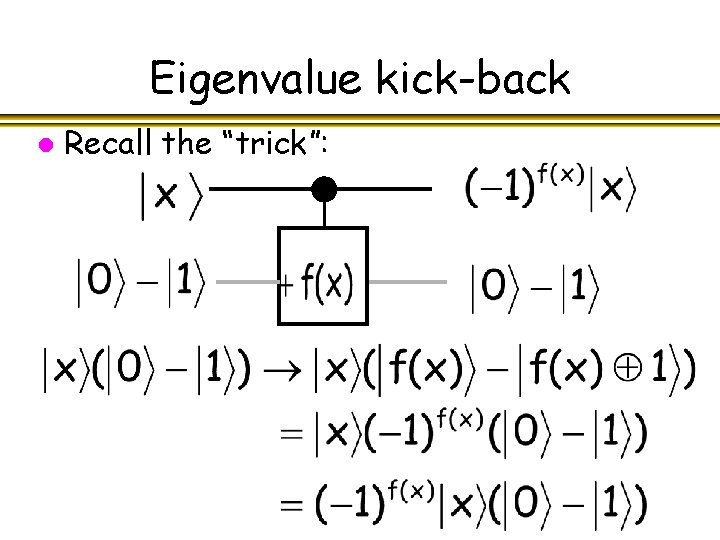
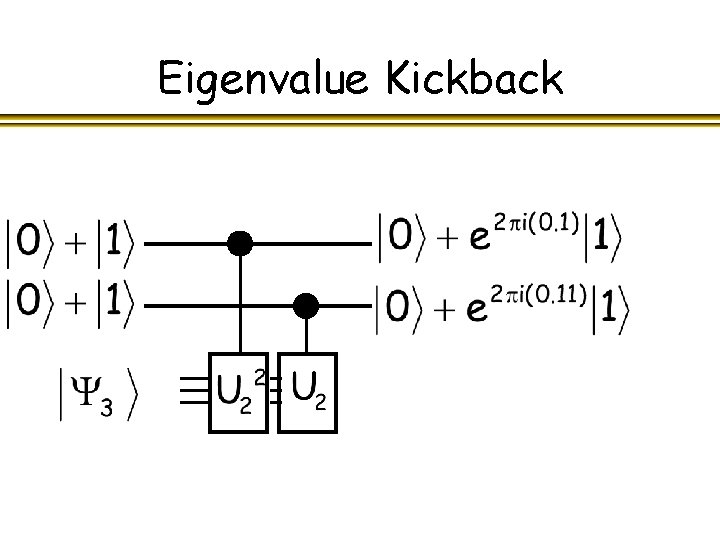
Eigenvalue kick-back l Recall the “trick”:

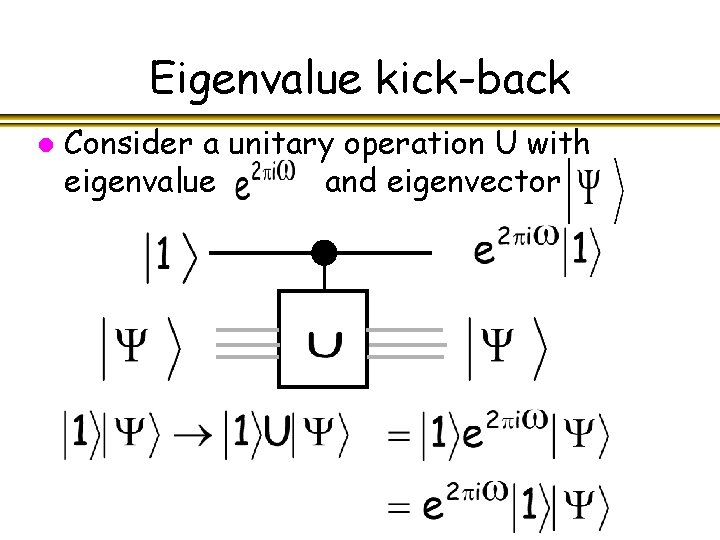
Eigenvalue kick-back l Consider a unitary operation U with eigenvalue and eigenvector

Eigenvalue kick-back

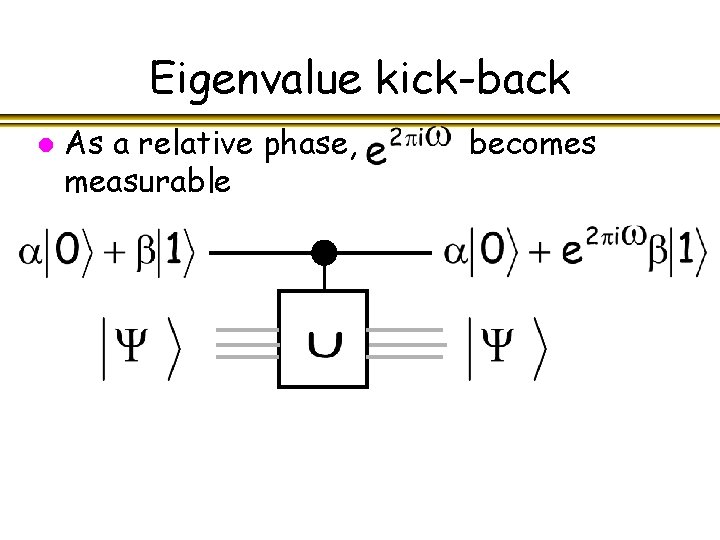
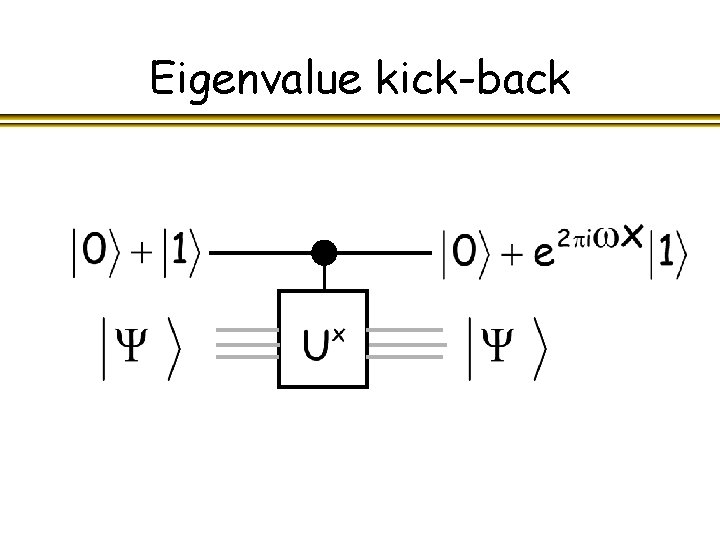
Eigenvalue kick-back l As a relative phase, measurable becomes

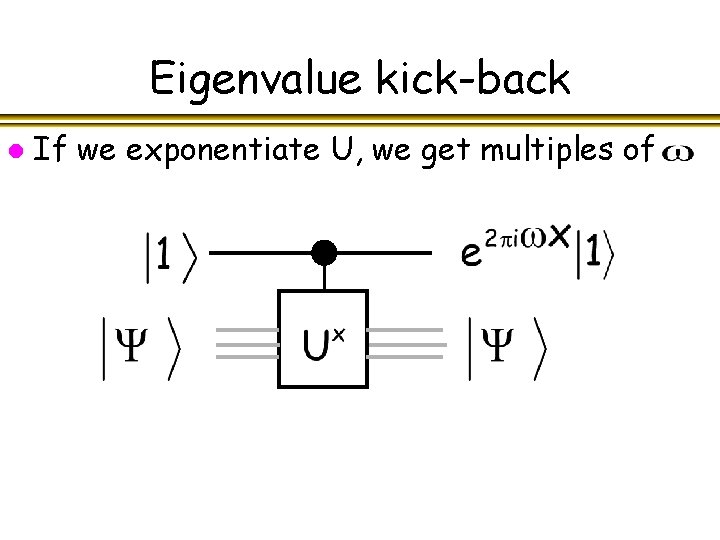
Eigenvalue kick-back l If we exponentiate U, we get multiples of

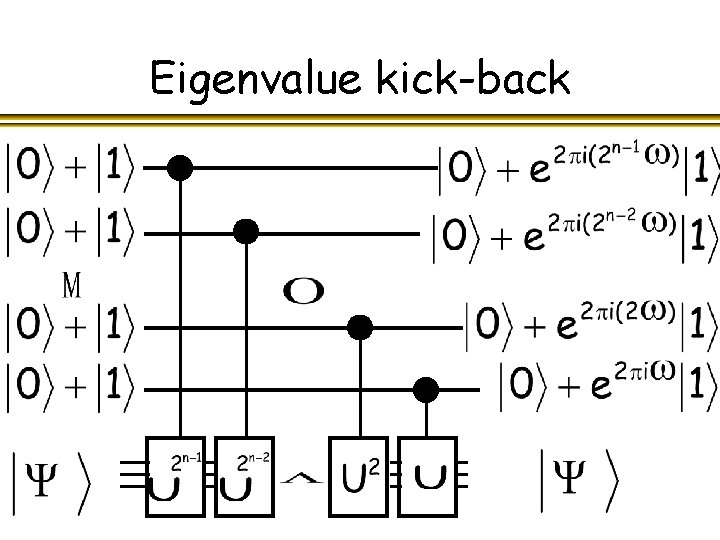
Eigenvalue kick-back

Eigenvalue kick-back

Phase estimation

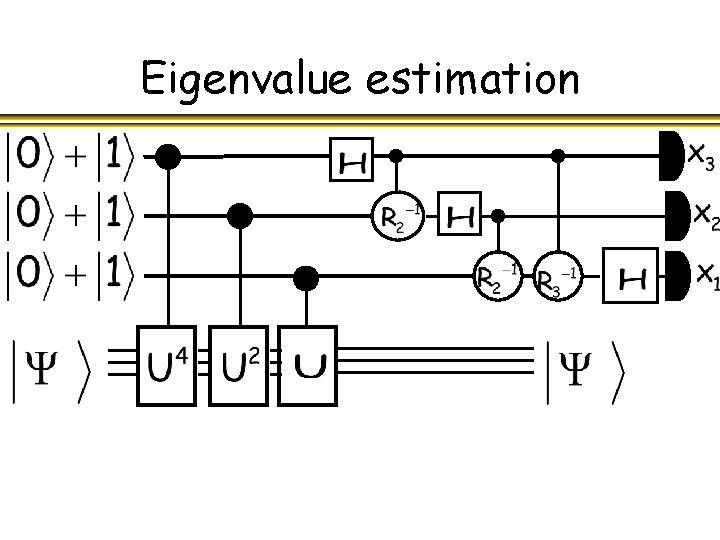
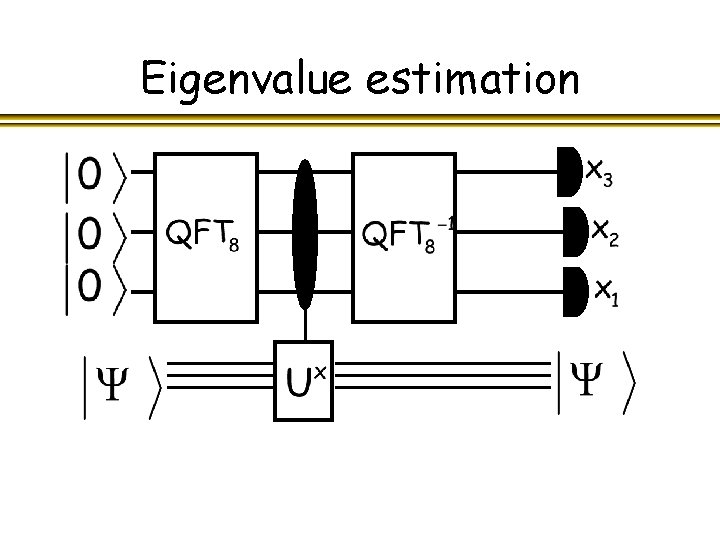
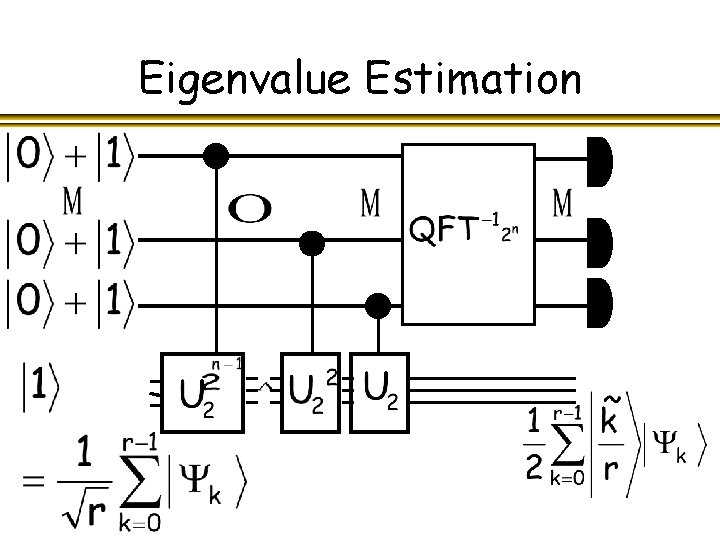
Eigenvalue estimation

Eigenvalue estimation

Eigenvalue estimation l Given with eigenvector and eigenvalue we thus have an algorithm that maps

Eigenvalue kick-back l Given with eigenvectors respective eigenvalues an algorithm that maps and therefore and we thus have

Eigenvalue kick-back l Measuring the first register of is equivalent to measuring probability i. e. with

Example Suppose we have a group and we wish to find the order of (I. e. the smallest positive such that ) l If we can efficiently do arithmetic in the group, then we can realize a unitary operator that maps l Notice that l l This means that the eigenvalues of are of the form where k is an integer

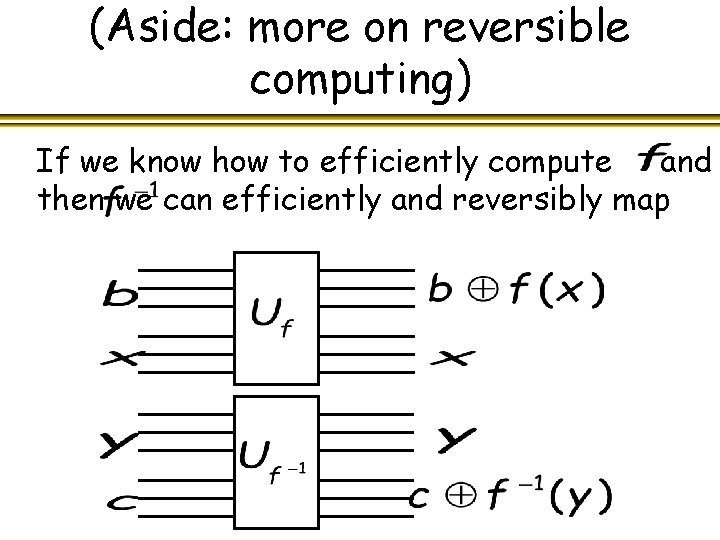
(Aside: more on reversible computing) If we know how to efficiently compute and then we can efficiently and reversibly map

(Aside: more on reversible computing) And therefore we can efficiently map

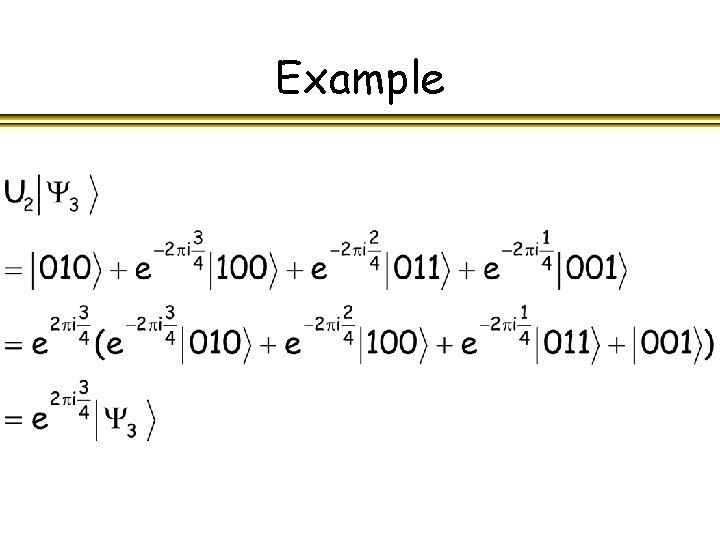
Example Let l Then l We can easily implement, for example, l l The eigenvectors of include

Example

Example

Example
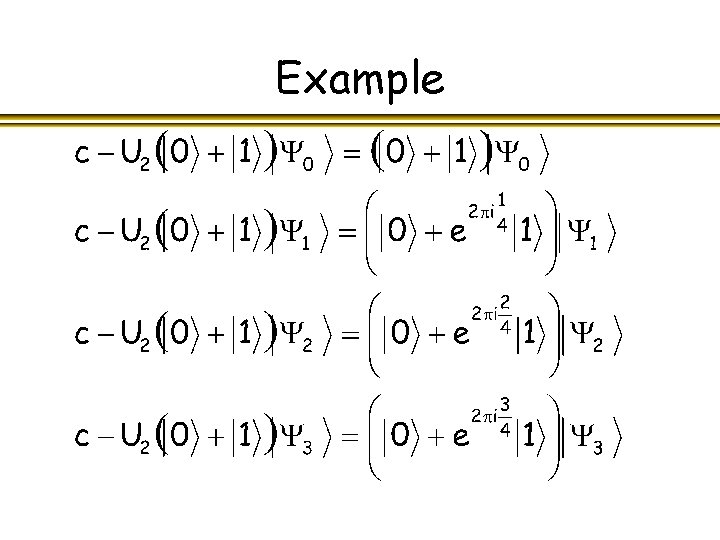
Example

Example

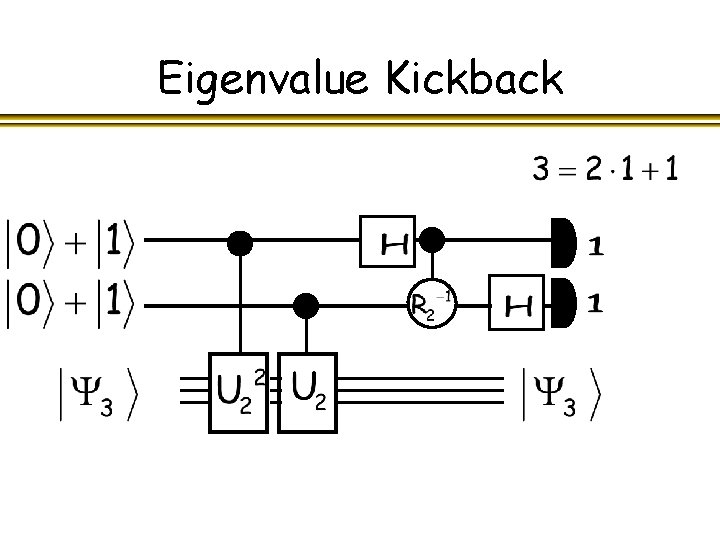
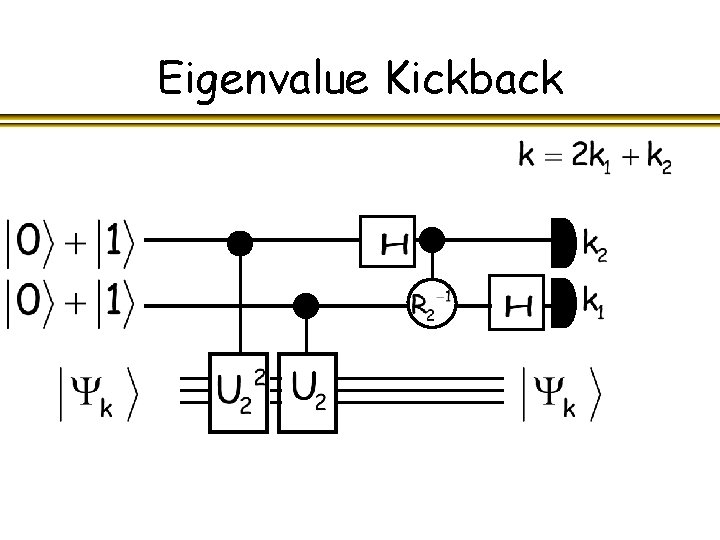
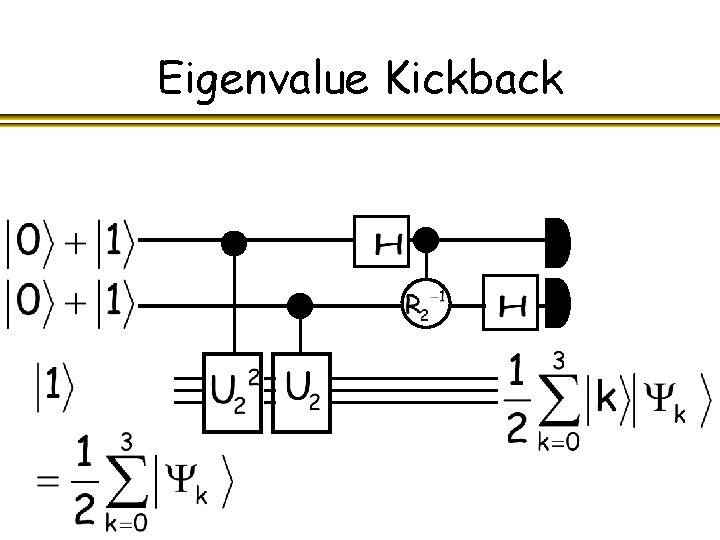
Eigenvalue Kickback

Eigenvalue Kickback

Eigenvalue Kickback

Eigenvalue Kickback

Quantum Factoring The security of many public key cryptosystems used in industry today relies on the difficulty of factoring large numbers into smaller factors. l Factoring the integer N into smaller factors can be reduced to the following task: Given integer a, find the smallest positive integer r so that l

Example Let l We can easily implement l l The eigenvectors of include

Example

Example

Eigenvalue kick-back l Given with eigenvectors respective eigenvalues an algorithm that maps and therefore and we thus have

Eigenvalue Estimation

Eigenvalue kick-back l Measuring the first register of is equivalent to measuring probability with

Finding r For most integers k, a good estimate of (with error at most ) allows us to determine r (even if we don’t know k). (using continued fractions)

(aside: how does factoring reduce to order-finding? ? ) l The most common approach for factoring integers is the difference of squares technique: » “Randomly” find two integers x and y satisfying » So N divides » Hope that If r is even, then let so that l is non-trivial

Shor’s approach This eigenvalue estimation approach is not the original approach discovered by Shor l Kitaev developed an eigenvalue estimation approach (to the more general “Hidden Stabilizer Problem”) l We’ve presented the CEMM version here l

Discrete Fourier Transform l The discrete Fourier transform maps uniform periodic states, say with period r dividing N, and offset w, to a periodic state with period N/r.

Discrete Fourier Transform l The quantum Fourier transform maps vectors in a Hilbert space of dimension N according to

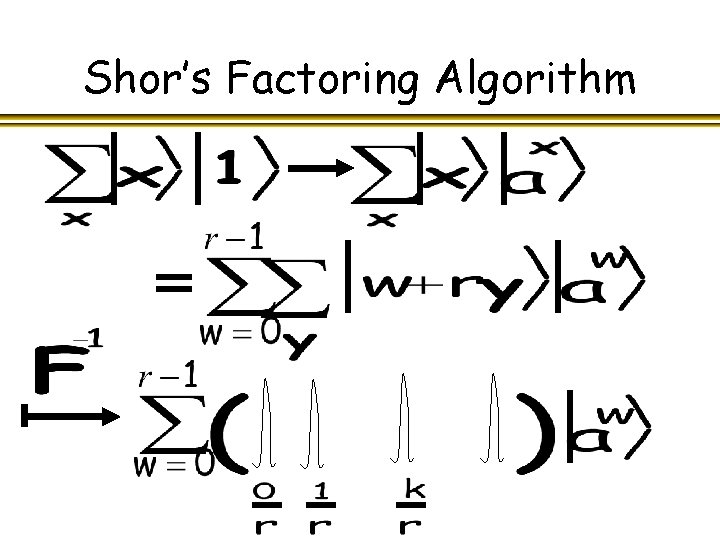
Shor’s Factoring Algorithm

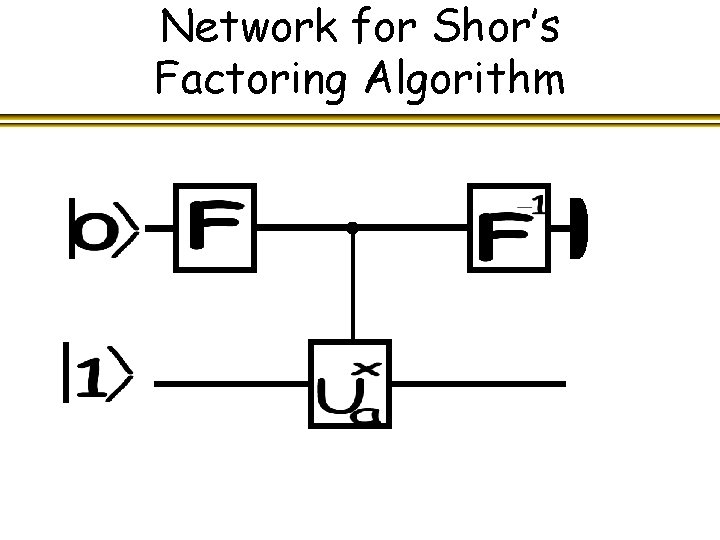
Network for Shor’s Factoring Algorithm

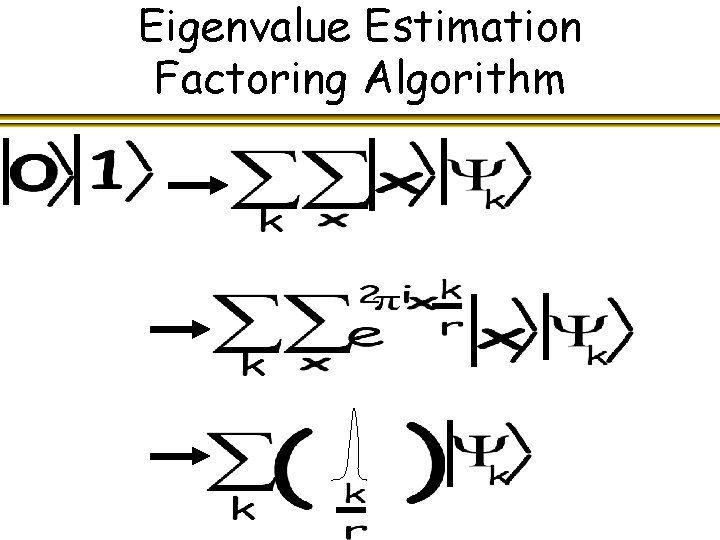
Eigenvalue Estimation Factoring Algorithm

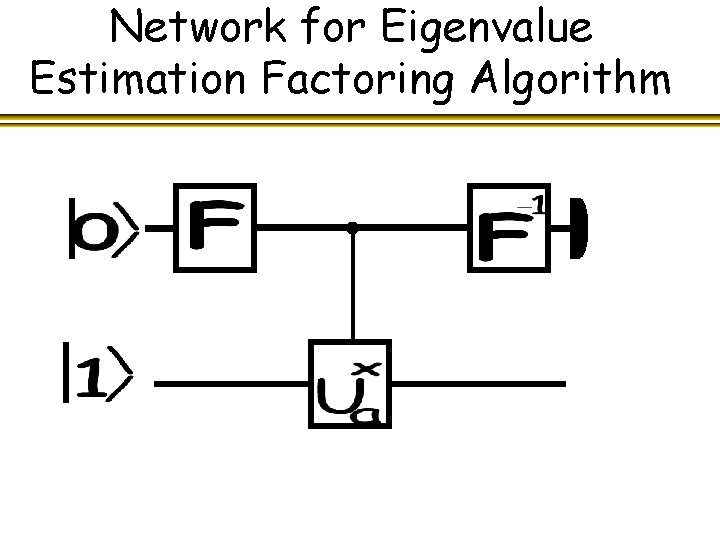
Network for Eigenvalue Estimation Factoring Algorithm

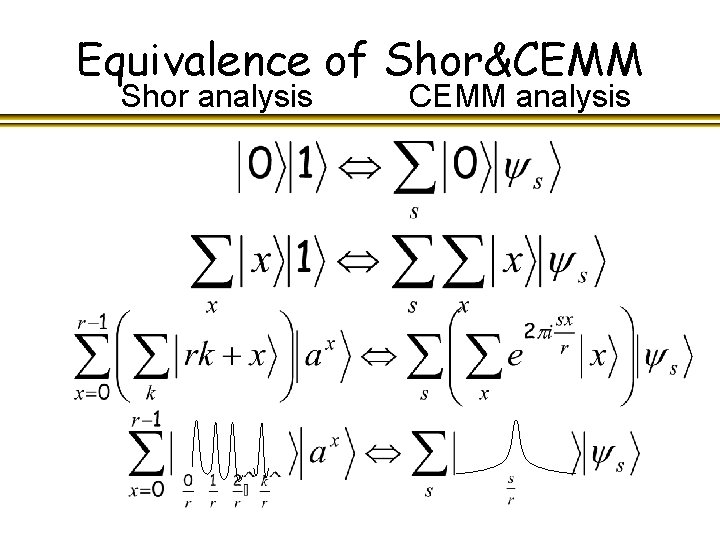
Equivalence of Shor&CEMM Shor analysis CEMM analysis

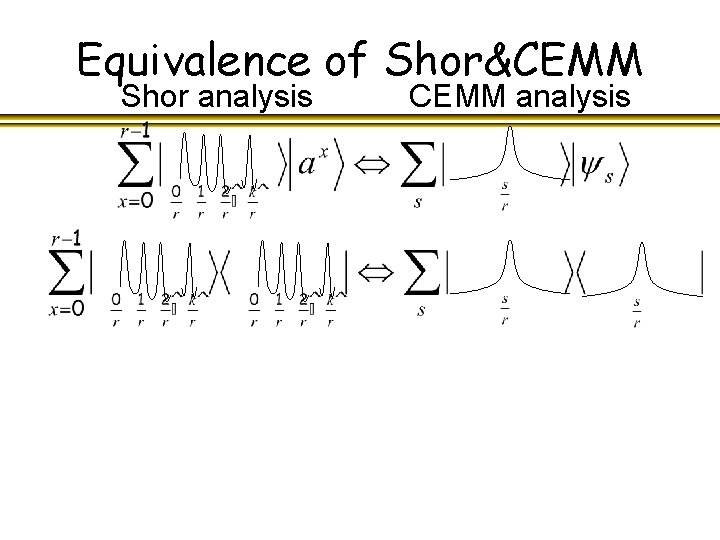
Equivalence of Shor&CEMM Shor analysis CEMM analysis

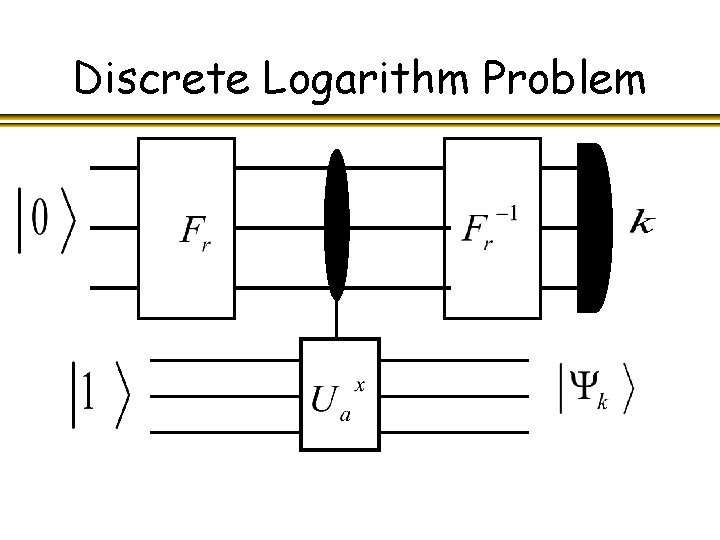
Discrete Logarithm Problem Consider two elements group G satisfying Find s. from a

Discrete Logarithm Problem We know has eigenvectors

Discrete Logarithm Problem Thus has the same eigenvectors but with eigenvalues exponentiated to the power of s

Discrete Logarithm Problem

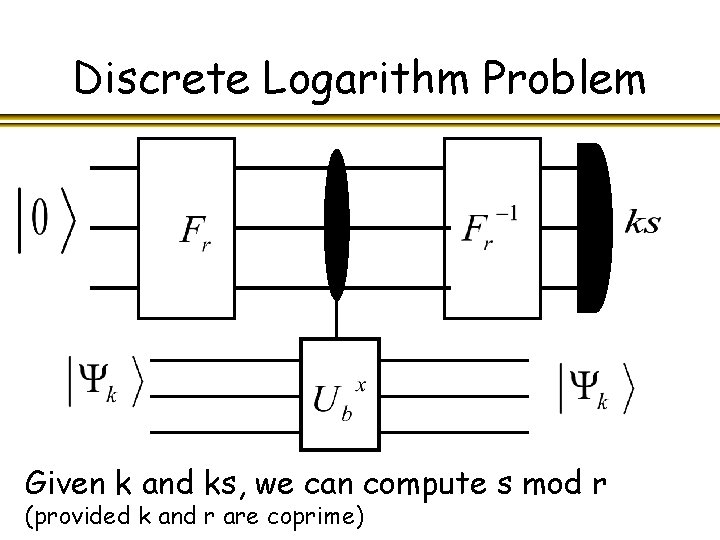
Discrete Logarithm Problem Given k and ks, we can compute s mod r (provided k and r are coprime)

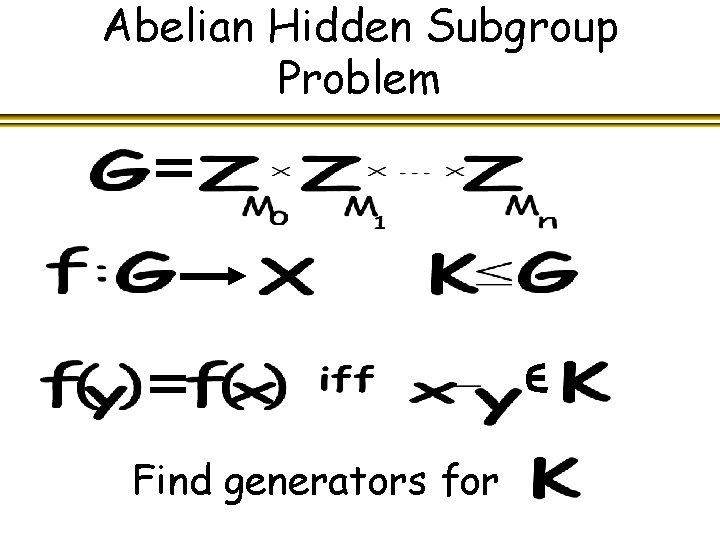
Abelian Hidden Subgroup Problem Find generators for

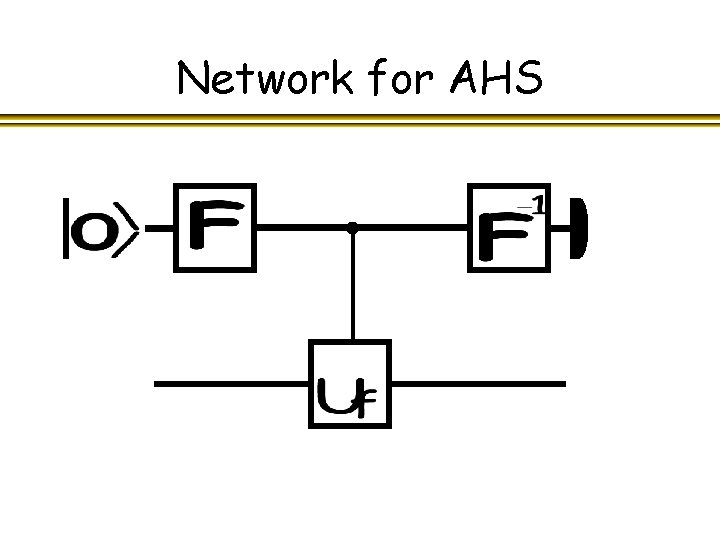
Network for AHS

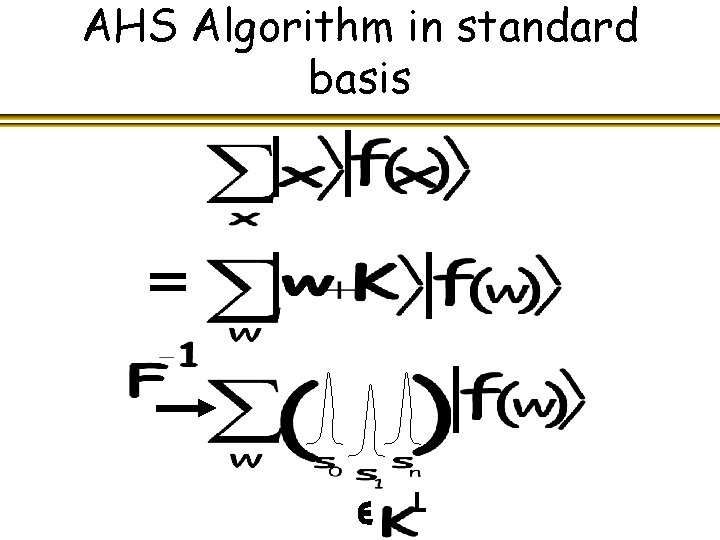
AHS Algorithm in standard basis
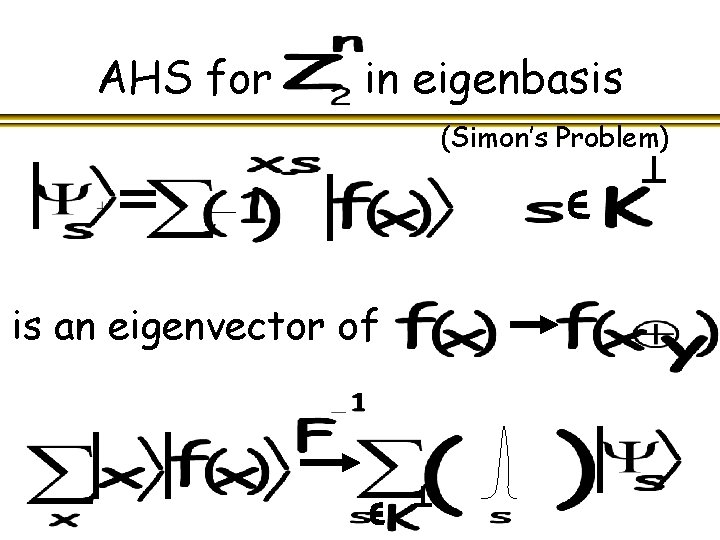
AHS for in eigenbasis (Simon’s Problem) is an eigenvector of

Other applications of Abelian HSP Any finite Abelian group G is the direct sum of finite cyclic groups l But finding generators satisfying is not always easy, e. g. for it’s as hard as factoring N l Given any polynomial sized set of generators, we can use the Abelian HSP algorithm to find new generators that decompose G into a direct sum of finite cyclic groups. l

Examples: Deutsch’s Problem: or Order finding: any group
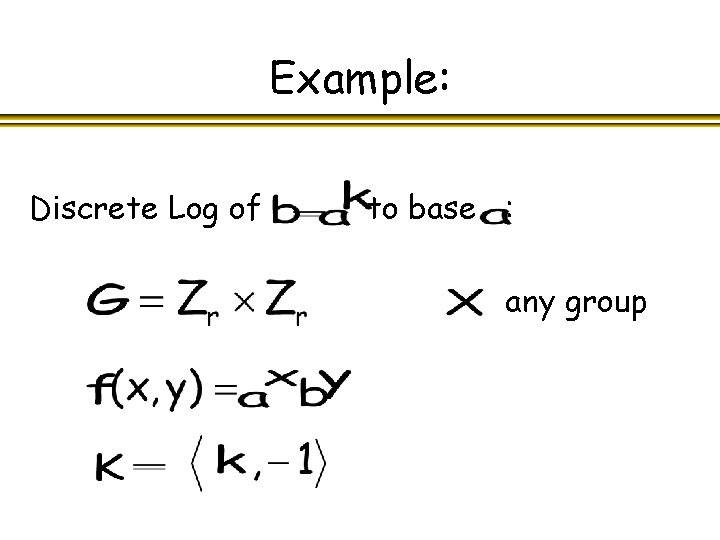
Example: Discrete Log of to base : any group

Examples: Self-shift equivalences:

What about non-Abelian HSP Consider the symmetric group l Sn is the set of permutations of n elements l Let G be an n-vertex graph l Let l Define l Then where l

Graph automorphism problem So the hidden subgroup of is the automorphism group of G l This is a difficult problem in NP that is believed not to be in BPP and yet not NPcomplete. l

Other Progress on the Hidden Subgroup Problem in non-Abelian groups (not an exhaustive list) • Ettinger, Hoyer arxiv. gov/abs/quant-ph/9807029 • Roetteler, Beth quant-ph/9812070 • Ivanyos, Magniez, Santha arxiv. org/abs/quant-ph/0102014 • Friedl, Ivanyos, Magniez, Santha, Sen quant-ph/0211091 (Hidden Translation and Orbit Coset in Quantum Computing); they show e. g. that the HSP can be solved for solvable groups with bounded exponent and of bounded derived series • Moore, Rockmore, Russell, Schulman, quant-ph/0211124