Quantum Computers Algorithms and Chaos Varenna 5 15

Quantum Computers, Algorithms and Chaos, Varenna 5 -15 July 2005 Quantum computation with solid state devices “Theoretical aspects of superconducting qubits” Rosario Fazio

Outline Lecture 1 - Quantum effects in Josephson junctions - Josephson qubits (charge, flux and phase) - qubit-qubit coupling - mechanisms of decoherence - Leakage Lecture 2 - Geometric phases - Geometric quantum computation with Josephson qubits - Errors and decoherence Lecture 3 - Few qubits applications - Quantum state transfer - Quantum cloning

Motivations Ø Quantum information protocols without external control üChoose a given model and use just the time evolution (less flexible but more stable) üEasier to implement in solid state systems Ø Implementation of Quantum communication schemes in solid state devices ü Josephson arrays in quantum communication

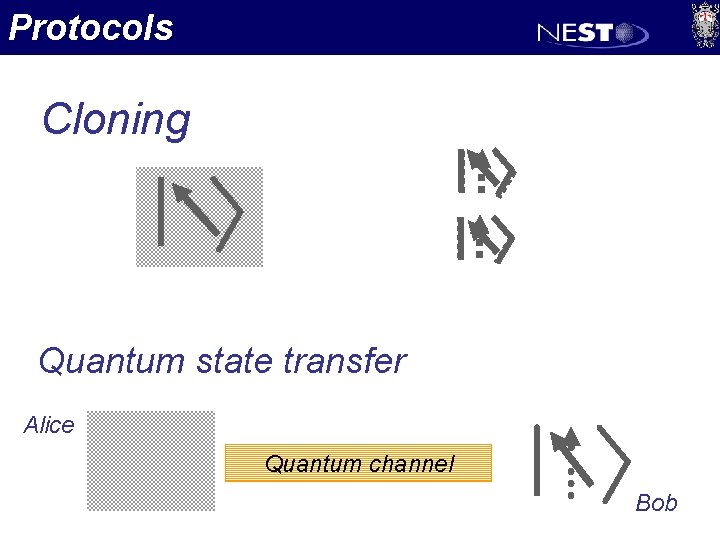
Protocols Cloning Quantum state transfer Alice Quantum channel Bob

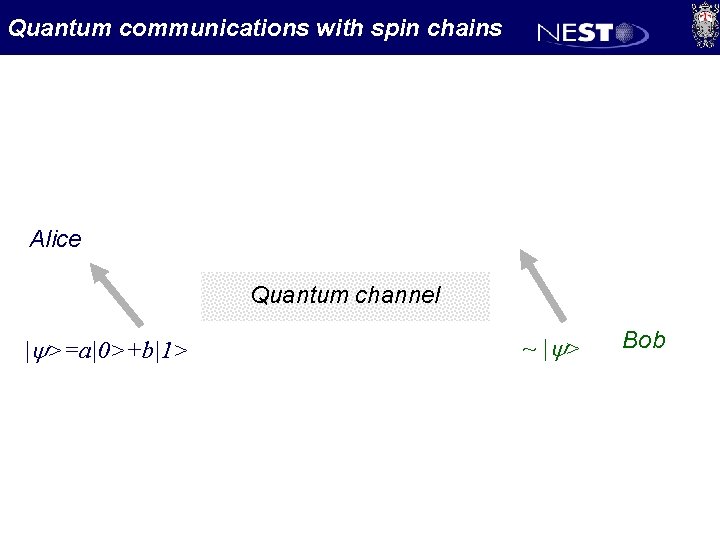
Quantum communications with spin chains Alice Quantum channel |y>=a|0>+b|1> ~ | y> Bob

Quantum communications with spin chains Alice . . . |y >qj J |0 > |0> Bob Initial state S. Bose (2002), M. Christandl et al (2003), F. Verstraete, M. Martin-Delgado and J. I. Cirac (2003), D. Burgarth and S. Bose (2004), D. Burgarth, V. Giovanetti and Bose (2005), V. Giovannetti and R. Fazio (2005), A. Romito, C. Bruder and R. Fazio (2005), G. De Chiara D. Rossini, S. Montangero and R. Fazio (2005), …

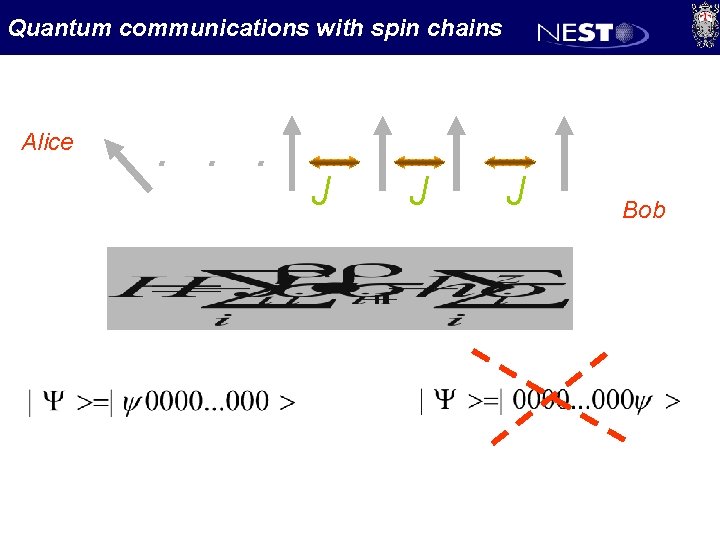
Quantum communications with spin chains Alice . . . J J J Bob

Quantum communications with spin chains • Initial state • Time evolution • Sender at site 1 • Receiver at site L

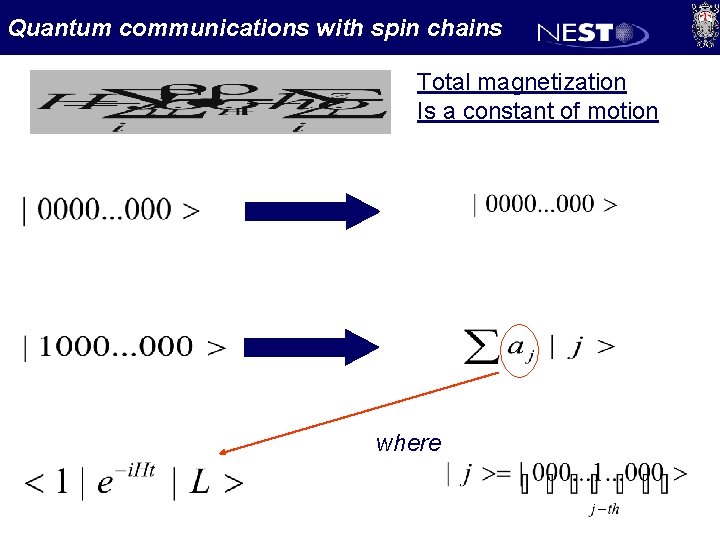
Quantum communications with spin chains Total magnetization Is a constant of motion where

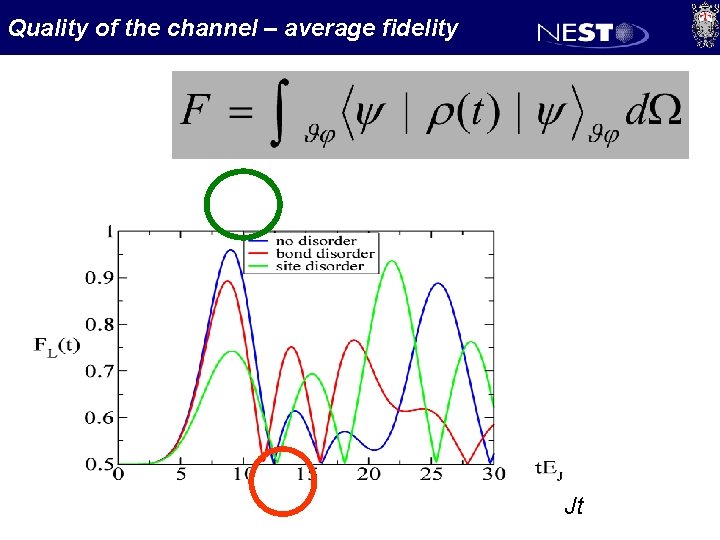
Quality of the channel – average fidelity Jt

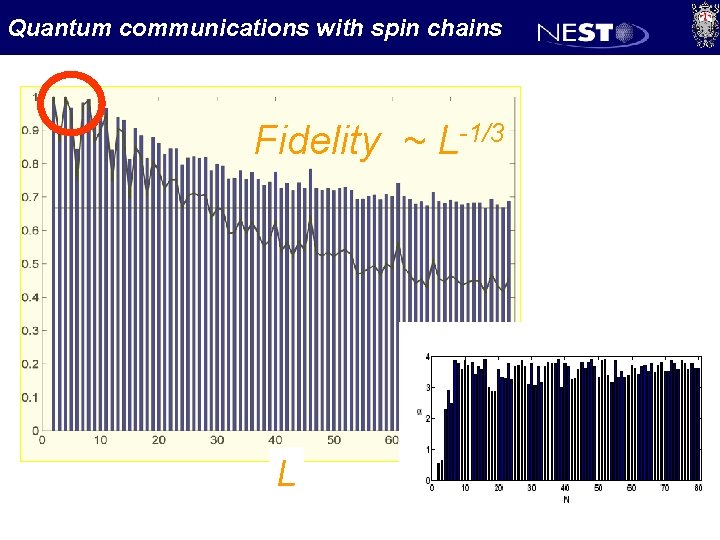
Quantum communications with spin chains Fidelity ~ L-1/3 L

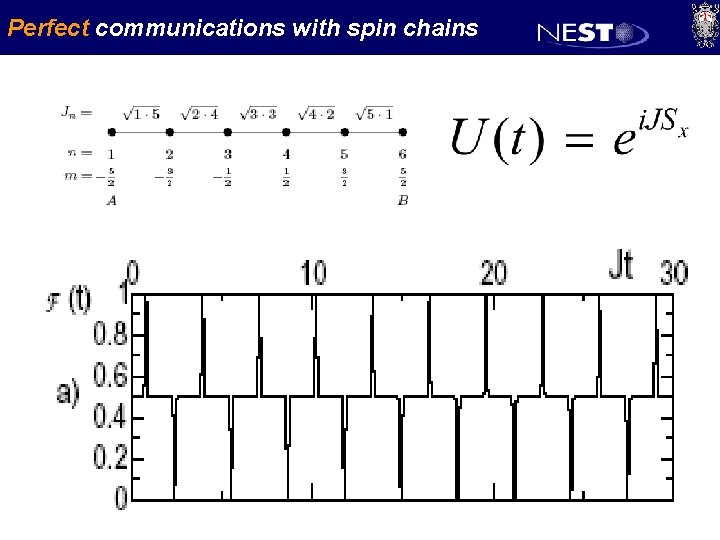
Perfect communications with spin chains

Quantum cloning A quantum copying machine does not exist! W. Wootters and W. Zurek (1982) No cloning theorem U|a>|0> U(|a>+|b>) |0> |a>|a> |aa>+|bb> ≠ (|a>+|b>)

Quantum cloning Although perfect cloning is not possible …. . … Imperfect cloning has been considered V. Buzek and M. Hillery (1996), D. Bruβ et al (1998), D. Bruβ, A. Ekert and C. Macchiavello (1998), R. Werner (2000), … A. Lama-Linares et al (2002), De Martini et al (2004), J. Du et al (2004), …

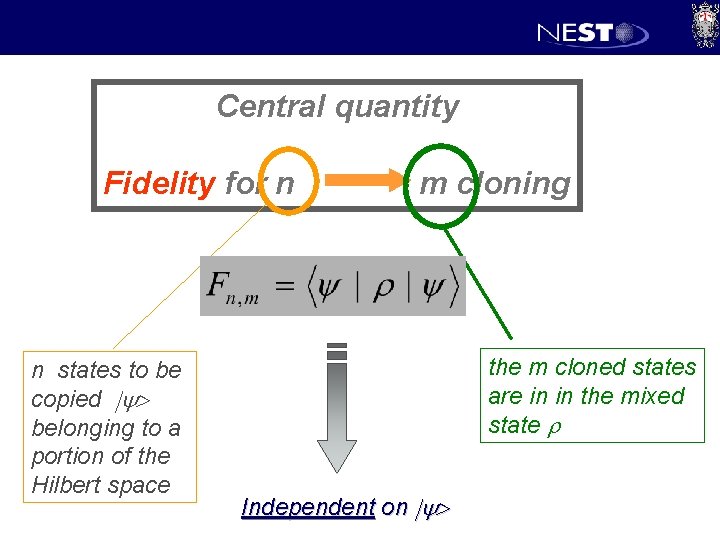
Central quantity Fidelity for n n states to be copied |y> belonging to a portion of the Hilbert space m cloning the m cloned states are in in the mixed state r Independent on |y>

Examples Universal Cloner Phase Covariant Cloner Fidelity at the equator

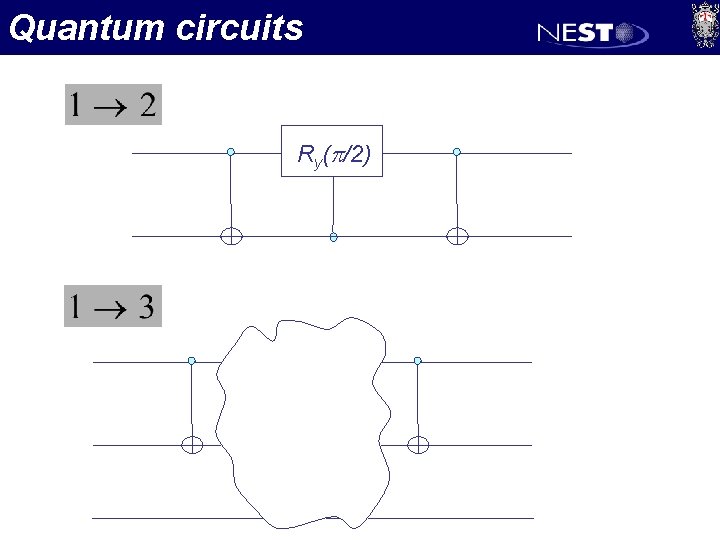
Quantum circuits Ry(p/2)

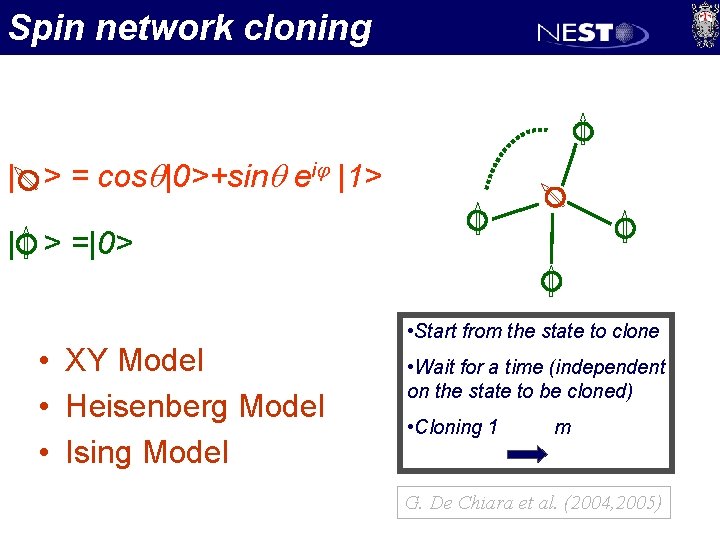
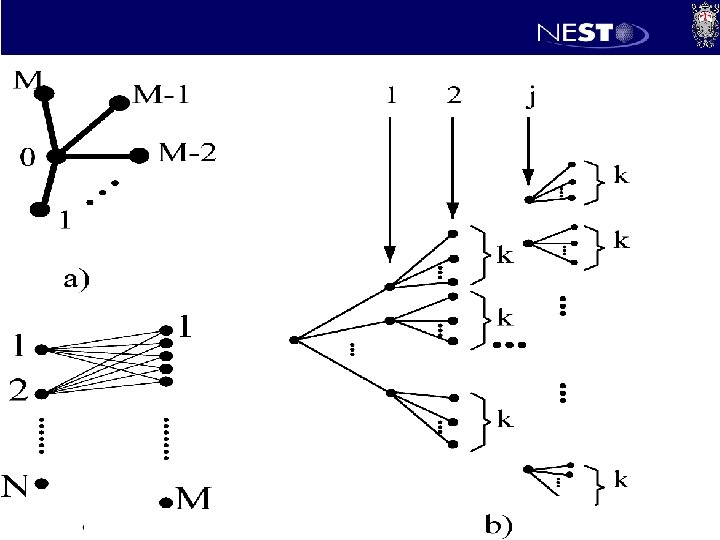
Spin network cloning | > = cosq|0>+sinq eij |1> | > =|0> • XY Model • Heisenberg Model • Ising Model • Start from the state to clone • Wait for a time (independent on the state to be cloned) • Cloning 1 m G. De Chiara et al. (2004, 2005)

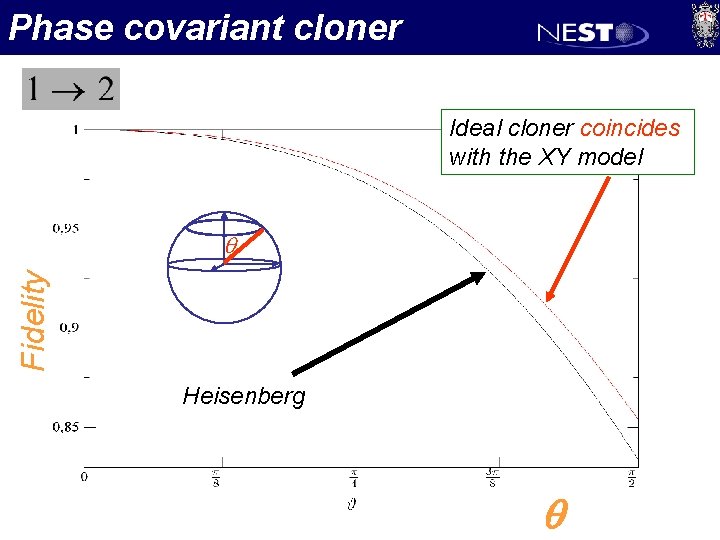
Phase covariant cloner Ideal cloner coincides with the XY model Fidelity q Heisenberg q

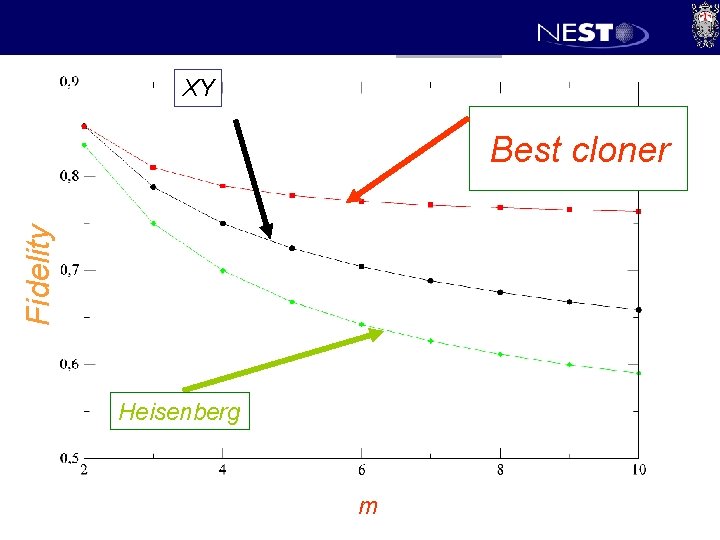
XY Fidelity Best cloner Heisenberg m

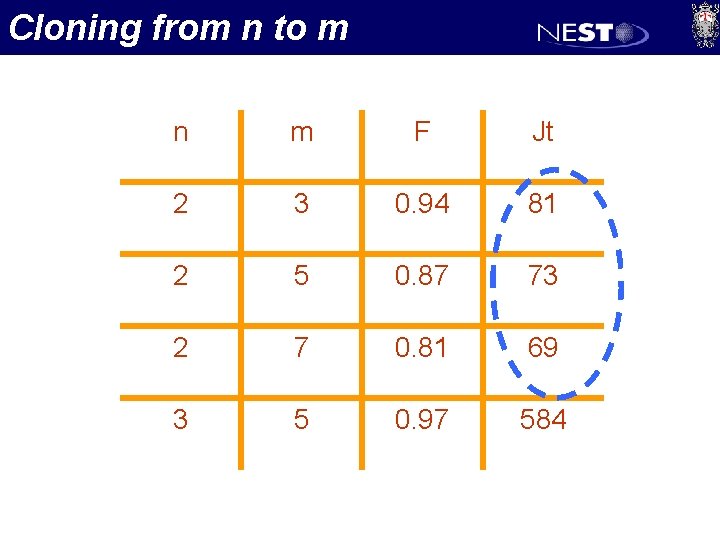
Cloning from n to m n m F Jt 2 3 0. 94 81 2 5 0. 87 73 2 7 0. 81 69 3 5 0. 97 584

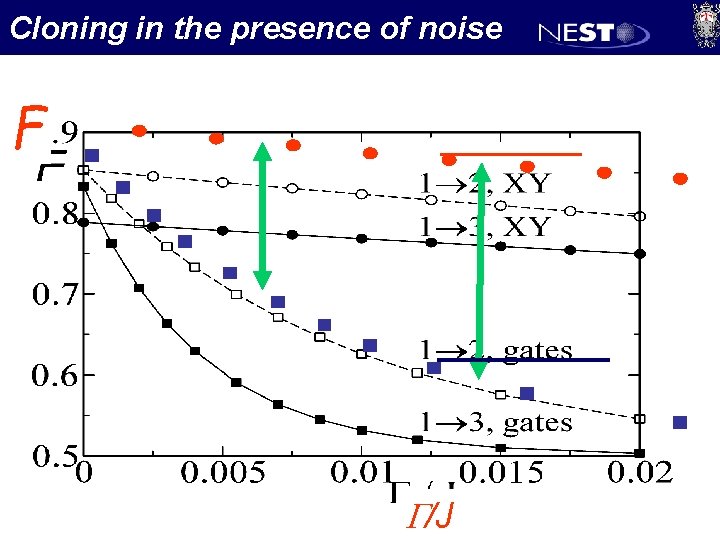
Cloning in the presence of noise F G/J

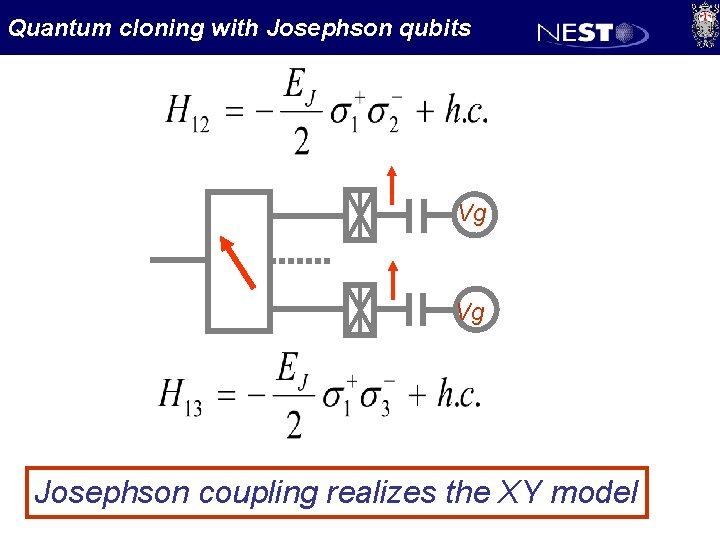
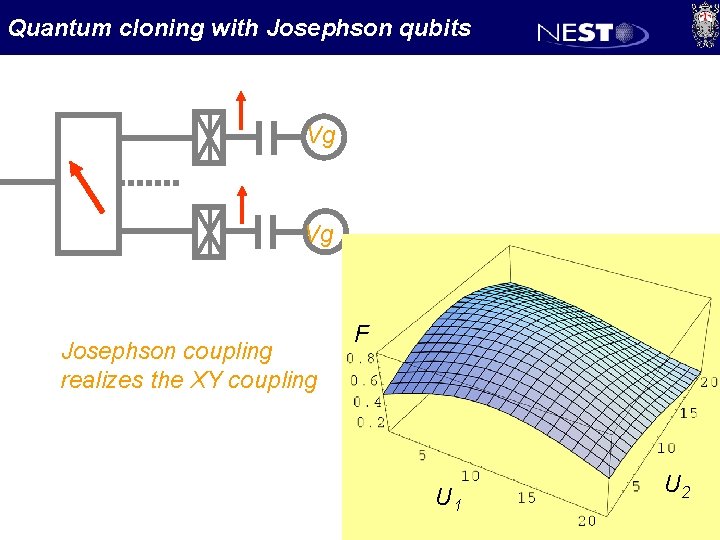
Quantum cloning with Josephson qubits Vg Vg Josephson coupling realizes the XY model

Quantum cloning with Josephson qubits Vg Vg Josephson coupling realizes the XY coupling F U 1 U 2

Quantum communication with JJA Josephson arrays as artificial 1 D magnets Bose-Hubbard = Quantum Phase Model = XXZ model Charge regime - C. Bruder R, Fazio, G. Schön, PRB 47, 342 (1993) Flux regime - L. Levitov, T. P. Orlando, J. B. Mayer, J. E. Mooij cond-mat 0108266

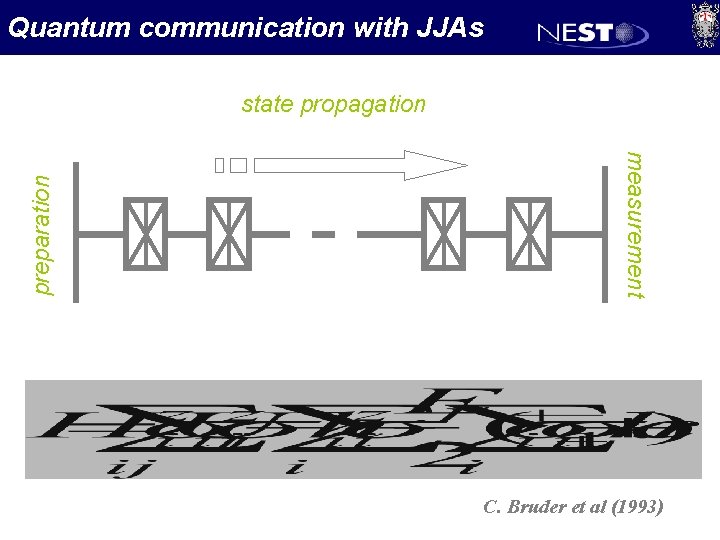
Quantum communication with JJAs measurement preparation state propagation C. Bruder et al (1993)

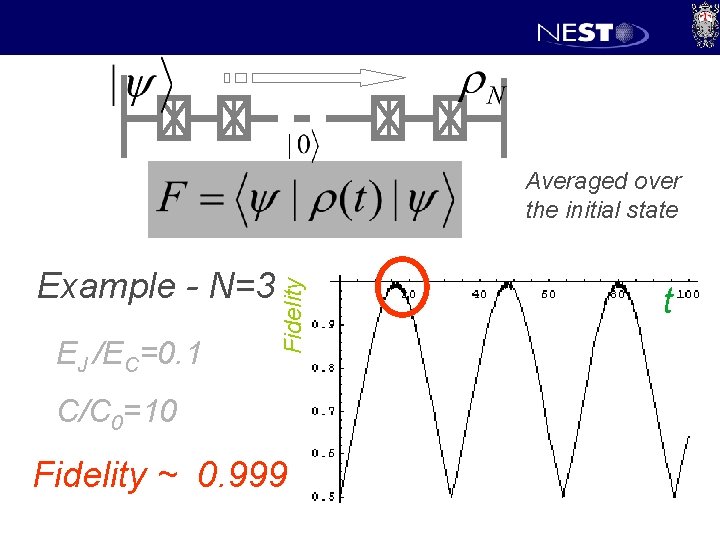
Example - N=3 EJ /EC=0. 1 Fidelity Averaged over the initial state C/C 0=10 Fidelity ~ 0. 999 t

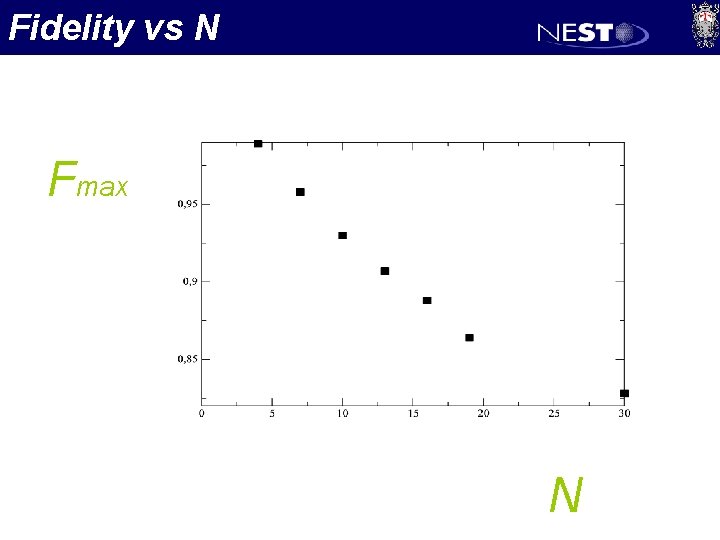
Fidelity vs N Fmax N

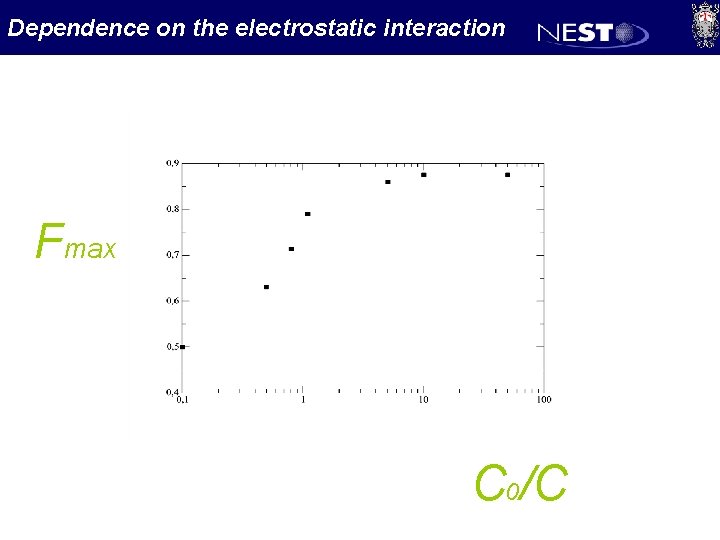
Dependence on the electrostatic interaction Fmax C 0/C

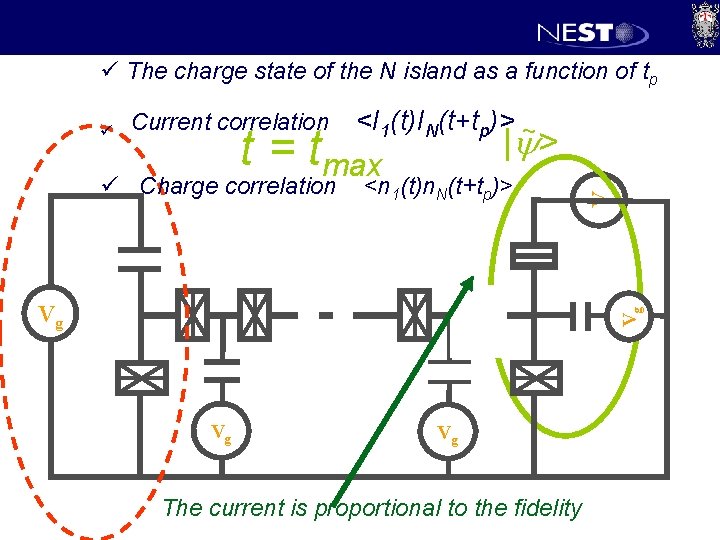
ü The charge state of the N island as a function of tp Current correlation <I 1(t)IN(t+tp)> ~ | y> t = tmax ü Charge correlation <n 1(t)n. N(t+tp)> Vg Vg V ü Vg Vg The current is proportional to the fidelity

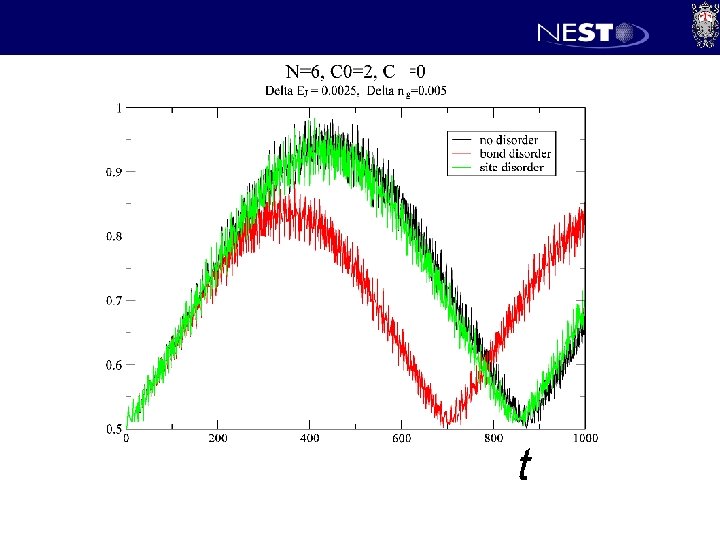
Imperfections – N=3 d. EJ/EJ=10% dnx/nx=10% Fidelity ~ 0. 95

t

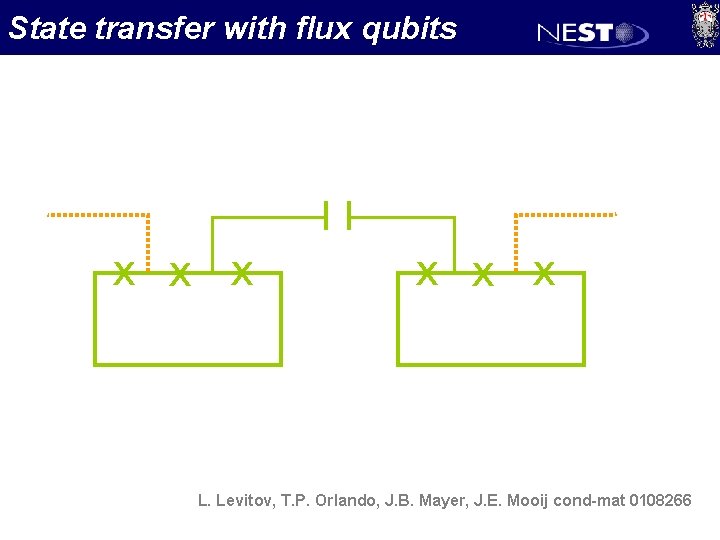
State transfer with flux qubits x x x L. Levitov, T. P. Orlando, J. B. Mayer, J. E. Mooij cond-mat 0108266

Entanglement sharing Alice { { Quantum channel ……………………. . Entangled Bob

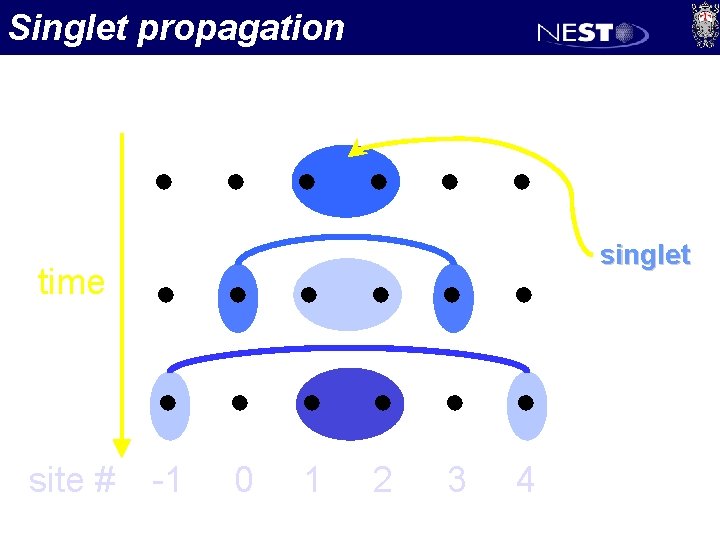
Singlet propagation ● time site # ● ● ● singlet ● ● ● -1 0 1 2 3 4

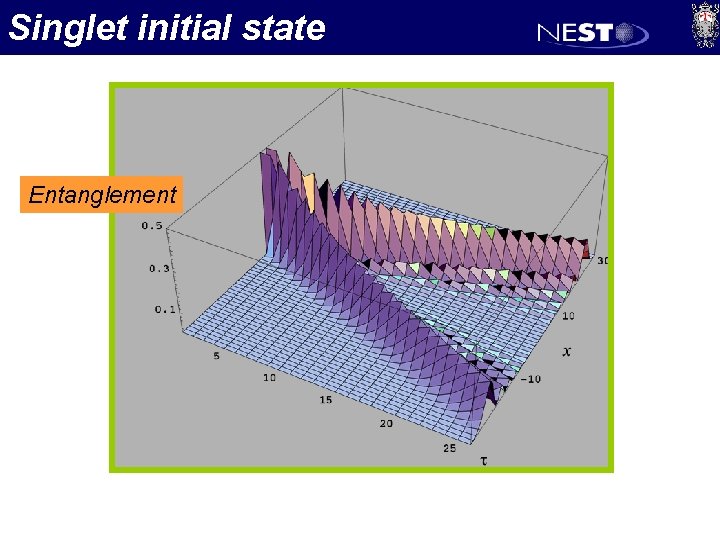
Singlet initial state Entanglement

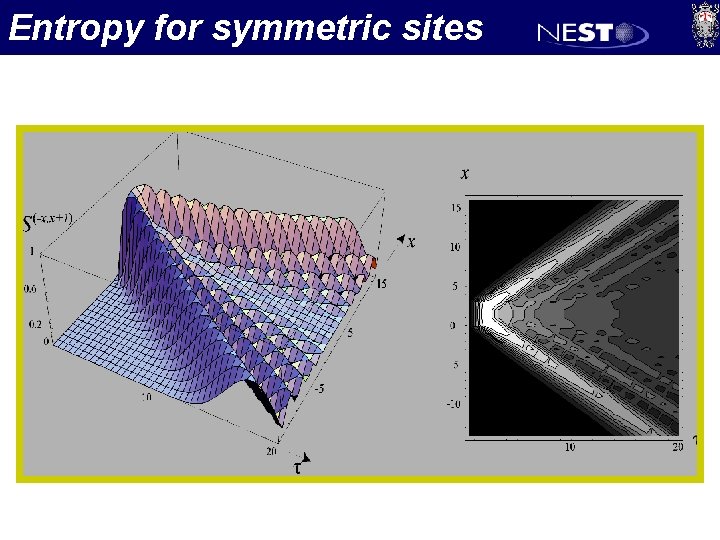
Entropy for symmetric sites

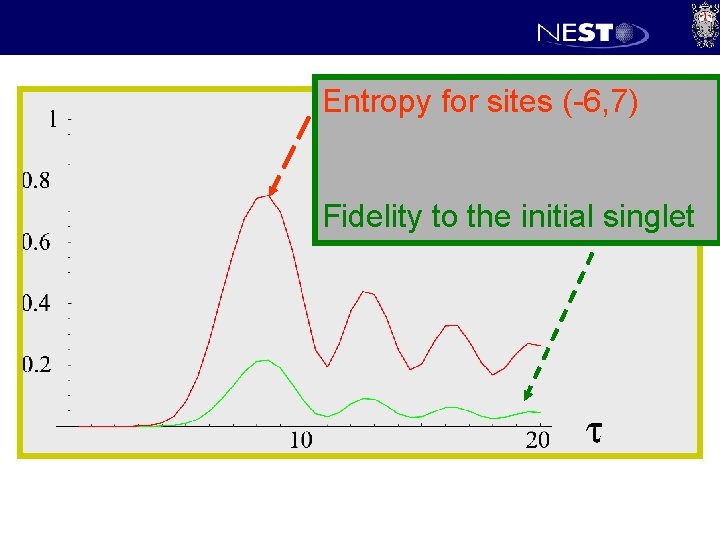
Entropy for sites (-6, 7) Fidelity to the initial singlet

Conclusions ü JJ arrays can be used in quantum communication § Entanglement sharing § Quantum Cloning § State transfer ü Experiments seems to be possible at present