Proving Analytic Inequalities Avi Wigderson IAS Princeton Math

Proving Analytic Inequalities Avi Wigderson IAS, Princeton Math and Computation New book on my website

Past 2 lectures Alternate minimization & Symbolic matrices: analytic algorithms for algebraic problems. Polynomial identities: algebraic tools for understanding analytic algorithms. Today Applications: Analysis & Optimization

Ubiquity of matrix tuples [GGOW’ 15’ 16] Computational Complexity (A 1, A 2, …, Am): symbolic matrix i. Aixi Quantum Information Theory (A 1, A 2, …, Am): completely positive operator Non-commutative Algebra In P (A 1, A 2, …, Am): rational expression In P (A 1, A 2, …, Am): orbit under Left-Right action In P (A 1, A 2, …, Am): projectors in Brascamp-Lieb inequalities In P (A 1, A 2, …, Am): exp size linear programs In P Invariant Theory Analysis Optimization

Brascamp-Lieb Inequalities [BL’ 76, Lieb’ 90] ∫ ∏j fj ≤ C ∏j |fj|pj Propaganda: special cases & extensions Cauchy-Schwarz, Holder Loomis-Whitney Young’s convolution Lieb’s Non-commutative BL Bennett-Bez Nonlinear BL Precopa-Leindler Nelson Hypercontractive Brunn-Minkowski Barthe Reverse BL Quantitative Helly Analysis, Geometry, Probability, Information Theory, …

Brascamp-Lieb Inequalities [BL’ 76, Lieb’ 90] Input B = (B 1, B 2, …, Bm) Bj: Rn Rnj (BL data) p = (p 1, p 2, …, pm) pj ≥ 0 ∫x Rn linear ∏j fj(Bj(x)) ≤ C ∏j |fj|pj ( fj: Rnj R+ integrable ) f = (f 1, f 2, …, fm) [Garg-Gurvits-Oliveira-W’ 16] Feasibility & Optimal C in P (through Operator Scaling & Alternate Minimization) Optimization: solving (some) exponential size LPs

Plan - Examples - General statement - Structural theory - Algorithm - Consequences: Structure Optimization (? ) Notation f: Rd R+ |f|1/p = (∫x Rd f(x)1/p)p

Examples

Cauchy-Schwarz, Holder d=1 f 1, f 2: R R+ [CS] ∫x R f 1(x)f 2(x) ≤ |f 1|2|f 2|2 p 1=p 2=1/2 any other norms? [H] ∫x R f 1(x)f 2(x) ≤ |f 1|1/p 1|f 2|1/p 2 p 1+p 2=1 pi≥ 0

Loomis-Whitney I d=2, x=(x 1, x 2) f 1, f 2: R R+ [Trivial] ∫x R 2 f 1(x 1)f 2(x 2) = |f 1|1|f 2|1 p 1=p 2=1 x 2 a 2 A a 1 x 1 area(A) ≤len(a 1)len(a 2) H(Z 1 Z 2) ≤ H(Z 1)+H(Z 2)

Loomis-Whitney II d=3, x=(x 1, x 2, x 3) f 1, f 2, f 3: R 2 R+ [LW] ∫x R 3 f 1(x 2 x 3)f 2(x 1 x 3)f 3(x 1 x 2) ≤ |f 1|2|f 2|2|f 3|2 pi=½ x 2 A 23 x 3 A 12 any other norms? x 1 S A 13 H(Z 1 Z 2 Z 2) ≤ ½[H(Z 1 Z 2)+H(Z 2 Z 3)+H(Z 1 Z 3)] vol(S) ≤ [area(A 12)area(A 13)area(A 23)]1/2

Young I d=2, x=(x 1, x 2) [Young] x 1+x 2 ∫x R 2 f 1(x 1)f 2(x 2)f 3(x 1+2) ≤ (√ 3)/2 |f 1|3/2|f 2|3/2|f 3|3/2 pi=2/3 Any other norms? a 3 a 2 f 1, f 2, f 3: R R+ A a 1 area(A) ≤ (√ 3)/2 [len(a 1)len(a 2)len(a 3)]2/3 x 1

Young II d=2, x=(x 1, x 2) [Young] f 1, f 2, f 3: R 2 R+ ∫x R 2 f 1(x 1)f 2(x 2)f 3(x 1+2) ≤ C |f 1|1/p 1|f 2|1/p 2|f 3|1/p 3 p 1+p 2+p 3=2 1≥pi≥ 0 C = q 1 q 1 q 2 q 2 q 3 q 3 p 1 p 1 p 2 p 2 p 3 p 3 qi=1 -pi

Brascamp-Lieb Inequalities [BL’ 76, Lieb’ 90] Input B = (B 1, B 2, …, Bm) Bj: Rn Rnj (BL data) p = (p 1, p 2, …, pm) pj ≥ 0 ∫x Rn ∏j fj(Bj(x)) ≤ C ∏j |fj|1/pj f = (f 1, f 2, …, fm) ( fj: Rnj R+ integrable ) Given BL data (B, p): Is there a finite C? What is the smallest C? [ BL(B, p) ] [GGOW’ 16] Feasibility & Optimal C in P

Structure (look for similarities to lecture 1)

Feasibility: C<∞ [Bennett-Carbery-Christ-Tao’ 08] Input B = (B 1, B 2, …, Bm) Bj: Rn Rnj (BL data) p = (p 1, p 2, …, pm) pj ≥ 0 ∫x Rn ∏j fj(Bj(x)) ≤ C ∏j |fj|1/pj [BCCT’ 08] C<∞ iff p PB P B: fi (the Polytope of B) ∑j p j n j = n ∑j pj dim(Bj. V) ≥ dim(V) subspace V in Rm pj ≥ 0 (Exponentially many inequalities) Rank nondecreasing

BL-constant [Lieb’ 90] Input B = (B 1, B 2, …, Bm) Bj: Rn Rnj (BL data) p = (p 1, p 2, …, pm) pj ≥ 0 ∫x Rn ∏j fj(Bj(x)) ≤ C ∏j |fj|1/pj fi [Lieb’ 90] BL(B, p) is optimized when fj are Gaussian 1/cap(L) = BL(B, p)2 = sup ∏j det(Aj)pj Nonconvex Aj>0 det(∑j pj Bjt. Aj. Bj) for some completely positive operator L (B, p) B 1 B 2 Quiver B 3 reduction A 1 A 2 A 3 A 4

Algorithms

Geometric BL [Ball’ 89, Barthe’ 98] Input B = (B 1, B 2, …, Bm) Bj: Rn Rnj (BL data) p = (p 1, p 2, …, pm) pj ≥ 0 ∫x Rn ∏j fj(Bj(x)) ≤ C ∏j |fj|1/pj fi [B’ 89] (B, p) is geometric if (Projection) B jt = I n j (Isotropy) ∑j p j B j t B j = I n j [B’ 89] (B, p) geometric BL(B, p)=1 Doublystochastic

Alternate Minimization [GGOW’ 16] [B’ 89] (B, p) is geometric if (1) Bj. Bjt = Inj (2) ∑j pj Bjt. Bj = In j [Projection property] [Isotropy property] On input (B, p): attempt to make it geometric Repeat t=nc times: - Satisfy Projection (Right basis change) - Satisfy Isotropy (Left basis change) Converges quickly iff (B, p) is feasible [GGOW’ 16] - Feasibility (testing C<∞, p PB) in polynomial time - Weak separation oracle - Feasible (B, p) converges to geometric in polytime - Keeping track of changes approximates BL(B, p) - Structure: bounds & continuity of BL(B, p), LP bounds.

Optimization

Linear programming & Polytopes e 3 P = conv {0, e 1, e 2, … em} Rm e 2 = { p Rm: ∑j pj ≤ 1 pj ≥ 0 j [m] } 0 Membership Problem: Test if p P? e 1 Easy if P has few inequalities, in a large variety of settings with many inequalities, and when… [GGOW’ 16] P is a BL-polytope! B = (B 1, B 2, …, Bm) Bj: Rn Rnj PB: { p Rm: ∑j pj nj = n ∑j pj dim(Bj. V) ≥ dim(V) V ≤ Rn pj ≥ 0 ? ? Applications? ?

Optimization: linear programs with exponentially many inequalities BL polytopes capture Matroids M = {v 1, v 2, …… vm} vj Rn Exponentially many Inequalities VJ = {vj : j J} PM = conv {1 J: VJ is a basis} Rm = { p Rm: ∑j�J pj ≤ dim(VJ) J [m] pj ≥ 0 Bj: Rn R Bjx=<vj, x> [Fact] PB = PM j [m] } j [m]

Optimization: linear programs with exponentially many inequalities BL polytopes capture Matroid Intersection M = {v 1, v 2, …… vm} vj Rn N = {u 1, u 2, …… um} uj Rn PM, N = conv {1 J: VJ, UJ are bases} Rm [Edmonds] = {p Rm: ∑j pj ≤ dim(VJ) J [m] ∑j pj ≤ dim(UJ) J [m] pj ≥ 0 Bj: R 2 n R 2 Bjx=<vj, x. L>, <uj, x. R> [Vishnoi] PB = PM, N j [m] } j [m]

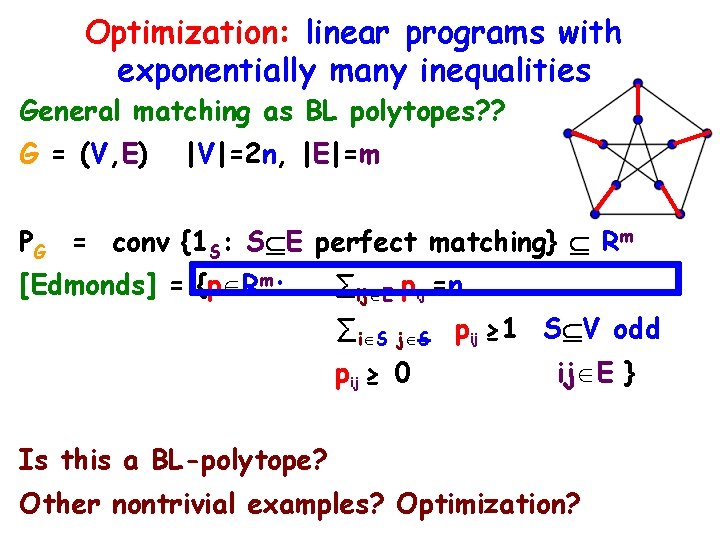
Optimization: linear programs with exponentially many inequalities General matching as BL polytopes? ? G = (V, E) |V|=2 n, |E|=m PG = conv {1 S: S E perfect matching} Rm [Edmonds] = {p Rm: ∑ij E pij =n ∑ i S j S pij ≥ 1 S V odd pij ≥ 0 ij E } Is this a BL-polytope? Other nontrivial examples? Optimization?

Summary One problem : Singularity of Symbolic Matrices One algorithm: Alternating minimization Non-commutative Algebra: Word problem Invariant Theory: Nullcone & orbit problems Quantum Information Theory: Positive operators Analysis: Brascamp-Lieb inequalities Optimization Exponentially large linear programs Computational complexity VP=VNP? Tools, applications, structure, connections, … Optimization, Complexity & Invariant Theory IAS workshop, June 4 -8, 2018