Games Computers and Computer Scientists Play Avi Wigderson

Games Computers (and Computer Scientists) Play Avi Wigderson

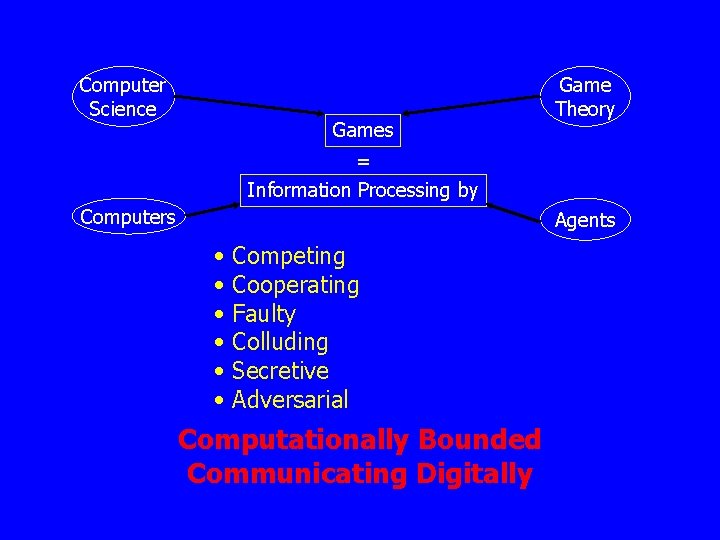
Computer Science Games Game Theory = Information Processing by Computers Agents • • • Competing Cooperating Faulty Colluding Secretive Adversarial Computationally Bounded Communicating Digitally

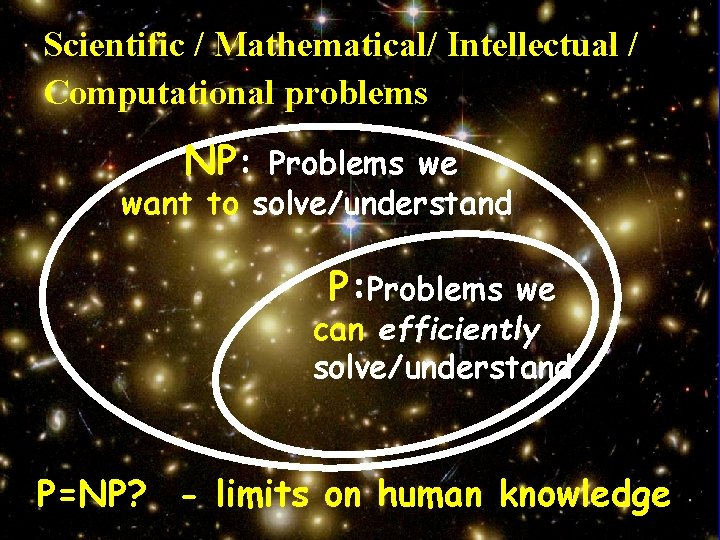
Scientific / Mathematical/ Intellectual / Computational problems NP: Problems we want to solve/understand P: Problems we can efficiently solve/understand P=NP? - limits on human knowledge

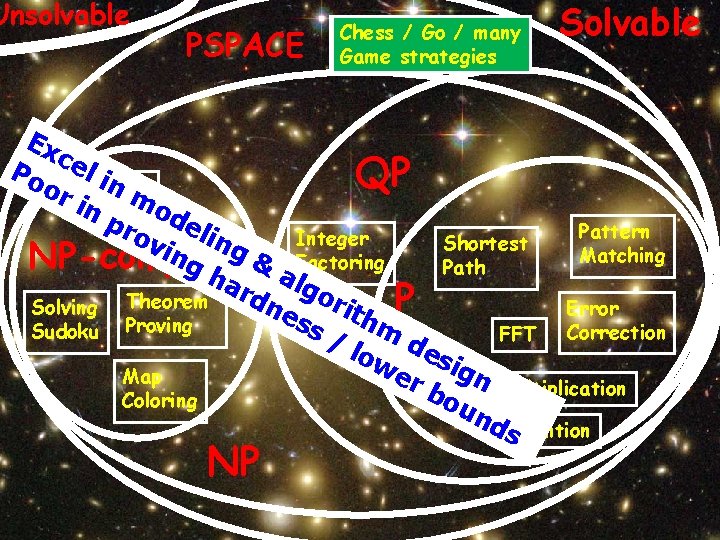
Unsolvable PSPACE Chess // Go Go // many game Game strategies Computation is everywhere Solvable Ex Po cel in QP or SAT in mod pro el Pattern Integer Shortest vin ing Matching NP-complete g h & a Factoring Path ard lgo ne rith P Solving Theorem Error ss Sudoku Proving FFT Correction / l m de ow sig er Map n Multiplication b ou Coloring nd Addition s NP

Plan • • Complexity of Games Design of Games against Clairvoyance Implementation of Games

Complexity of Games Perfect information Which of these games do you prefer playing? Why?

Theorem [Zermelo] : In every finite win/lose perfect information 2 -player game, White or Black can force a win. Extensive Form Q: Why play Chess or Tic-Tac-Toe? Q: Can a winning strategy be efficiently computed? Q: Can you state/prove analogous thm for 3 players?

Rectangle Game m=4 n=5 1 m 1 5 2 4 3 Rules: Each player in turn removes a token, and all those (remaining) to its north or east. Player taking the Red token loses n Theorem: 1 st player has a winning strategy. Proof: Assume 2 nd has a winning strategy. Then White can mimic it and win. Contradiction! Question: What is the winning strategy? Question: Do you like this game? Why?

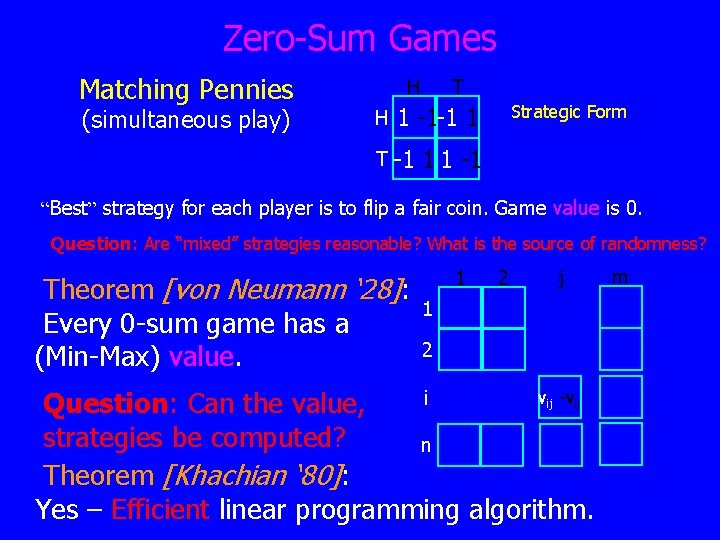
Zero-Sum Games Matching Pennies (simultaneous play) H H T Strategic Form 1 -1 -1 1 T -1 1 1 -1 “Best” strategy for each player is to flip a fair coin. Game value is 0. Question: Are “mixed” strategies reasonable? What is the source of randomness? Theorem [von Neumann ‘ 28]: Every 0 -sum game has a (Min-Max) value. 1 2 j 1 2 vij -vij i Question: Can the value, strategies be computed? n Theorem [Khachian ‘ 80]: Yes – Efficient linear programming algorithm. m

Nash Equilibrium Chicken [Aumann] C Probabilistic strategies (Sw, Sb). C D 11 20 Strategic Form D 0 2 -3 -3 Nash Equilibrium: No player has an incentive to change its strategy given the opponent’s strategy. here Sw=Sb = [C with prob ¾, D with prob ¼] Theorem [Nash]: Every (matrix) game has an equilibrium. Question: Can the players compute (any) equilibrium? Best known algorithm: exponential time (infeasible). Theorem[Chen, Daskalakis, Papadimitriou]: PPAD-complete Question: Is Nash Eq. a good notion of a “rational solution”?

Designing Games

How to minimze players’ influence What is the best Function? Public Information Model [Ben-Or—Linial] : Joint random coin flipping Function Every good player flips, then the bad, Parity Majority then combine majority parity M M M P M Influence 1 1/7 Iterated Majority 1/8 M Theorem [Kahn—Kalai—Linial] : For every function, some player has non-proportional influence: >c(log n)/n Theorem [Alon—Naor] : There are “multi-round” functions for which no player has non-proportional influence: <c/n

How to achieve cooperation, efficiency, truthfulness Players (agents) are selfish • Auction Question: How to get players to bid their true values? Theorem [Clarke—Groves—Vickery]: 2 nd price auction achieves truthfulness. • Internet / Distributed Games Question: How to get players to cooperate? [Nisan]: Distributed algorithmic mechanism design. [Papadimitriou]: Algorithms, Games & the Internet, Price of anarchy, complexity classes New CS Issues: Pricing, incentives New GT Issues: Complexity, Algorithms

Coping with Uncertainty Competing against Clairvoyance

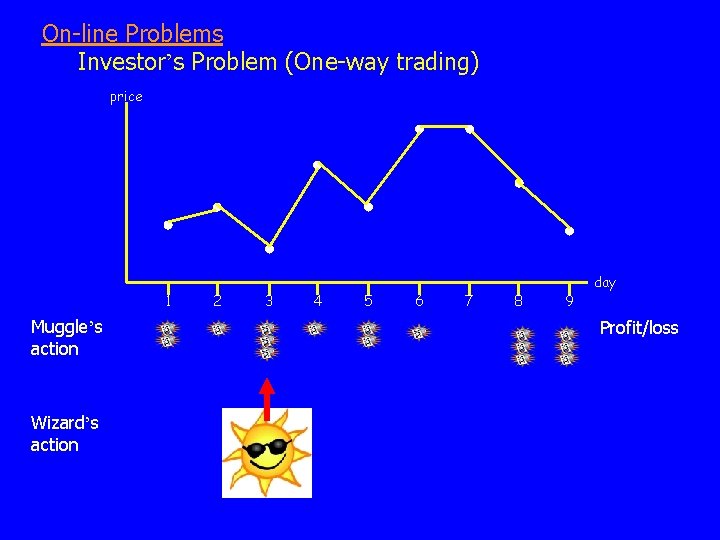
On-line Problems Investor’s Problem (One-way trading) price 1 Muggle’s action Wizard’s action 2 3 4 5 6 7 8 9 day Profit/loss

On-line problems are everywhere: • Computer operating systems • Taxi/Uber dispatchers • Investors’ decisions • Battle decisions • Weather prediction • • • Question: How to measure quality of on-line algs?

Competitive Analysis [Tarjan—Slator]: Bound the “competitive ratio”: muggle-cost(sequence) wizard-cost(sequence) Uniformly, over every sequence of events Can be achieved in many settings. Huge, successful theory. “Online Computation and Competitive Analysis” [Borodin—El-Yaniv] May be viewed as a repeated, 2 player game: An adversary, generating the sequence, and the muggle, responding to it!

The ski problem Problem: Rent or buy? Renting a pair of skis for 1 day: $100 Buying a pair of skis, for life: $1000 Day 1: ? Day 2: ? … … How many days D you’ll ski is uknown to Muggle, known to Wizard Muggle’s action: Rent for 9 days. On day 10 buy. Wizard’s action: If D>9, buy on Day 1. Else rent every day. Competitive ratio: <2 (if D=10, W pays $1000, M pays $1900)

Doing as well as the best of (k) experts Reality E 1, E 2, …. , Ek Day 0: Day 1: Day 2: Day 3: … Make as few prediction errors as possible Muggle

Implementing Games Q: Many games (and interactions) have rules / constraints – can they be played /implemented (eg on the phone, Internet)? The power of cryptography (and beyond)

The Millionaires’ Problem A Alice B Bob Both want to know who is richer Neither gets any other information Question: Is that possible?

Joint random decisions Nash eq. with Independent Strategies Expected value = 3/4 Prob[CC] = 9/16 Prob[CD] = 3/16 Prob[DC] = 3/16 Prob[DD] = 1/16 3/4 C 3/4 1/4 C D 11 20 1/4 D 0 2 -3 -3 Nash eq. with Correlated Strategies [Aumann] Prob[CD] = 1/2 Prob[DC] = 1/2 Prob[CC] = 0 Prob[DD] = 0 Expected value = 1 Question: How to flip a coin jointly?

Simultaneity 1/2 H Expected value = 0 (if they play simultaneously) T 1 -1 -1 1 1/2 H 1/2 T -1 1 1 -1 Question: How do we guarantee simultaneity? A computational representation: Parity Function outcome P x. W x. B Parity(x. W, x. B ) 0 1 0 1 1 0 0 0 1 1

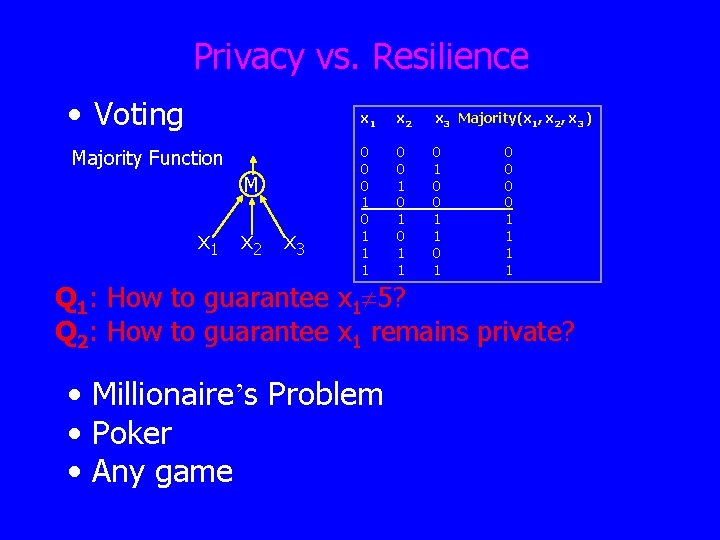
Privacy vs. Resilience • Voting Majority Function M x 1 x 2 x 3 Majority(x 1, x 2, x 3 ) 0 0 0 1 1 1 0 0 1 0 1 0 0 0 0 1 1 Q 1: How to guarantee x 1 5? Q 2: How to guarantee x 1 remains private? • Millionaire’s Problem • Poker • Any game

A Completeness Theorem [Yao, Goldreich –Micali –Wigderson]: 1: essential 1. More than 1/2 of the players are honest 2+3: crypto 2. Players computationally bounded 3. Trap-door functions exist (e. g. factoring integers is hard) Every game, with any secrecy requirements, can be digitally implemented s. t. no collusion of the bad players can affect: * correctness (rules, outcome) * privacy (no information leaks) Hard problems can be useful!

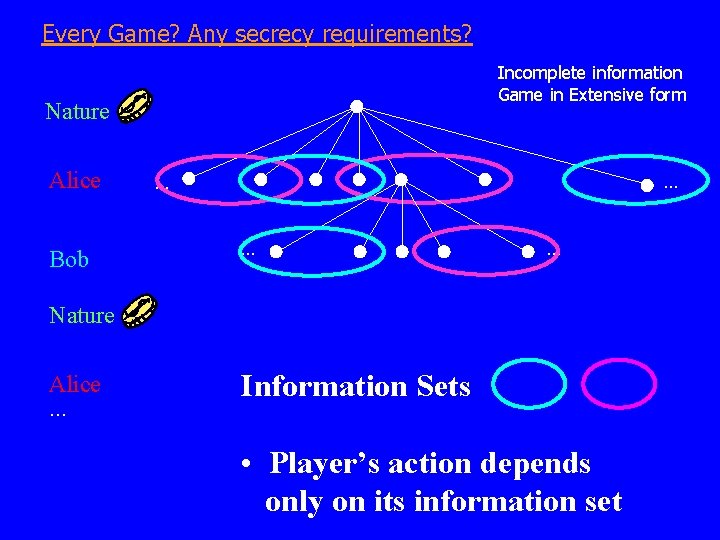
Every Game? Any secrecy requirements? Incomplete information Game in Extensive form Nature Alice Bob . . . Nature Alice. . . Information Sets • Player’s action depends only on its information set

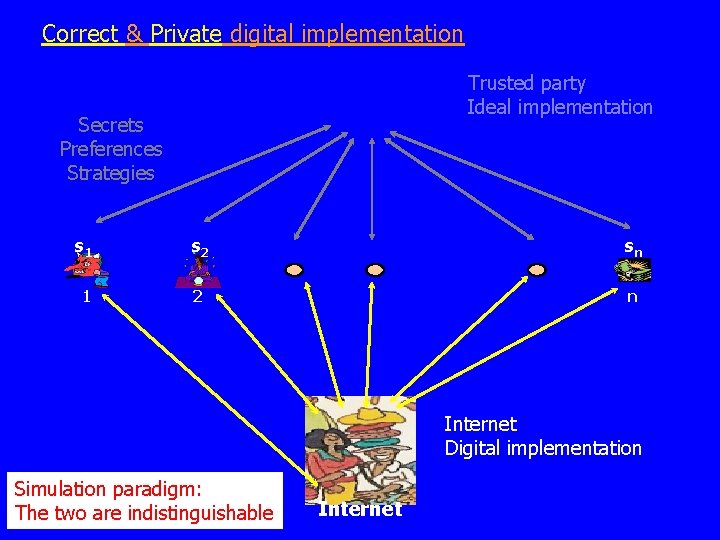
Correct & Private digital implementation Trusted party Ideal implementation Secrets Preferences Strategies s 1 s 2 sn 1 2 n Internet Digital implementation Simulation paradigm: The two are indistinguishable Internet

How to ensure Privacy Oblivious Computation [Yao] 1 f(inputs) P 1 1 0 M P 1 1 0 P M P 1 0 0 1 0

How to ensure Correctness Definition [Goldwasser-Micali-Rackoff]: zero-knowledge proofs: • Convincing • Reveal no information Theorem [Goldreich-Micali-Wigderson]: Every provable mathematical statement has a zero-knowledge proof. Corollary: Players can be forced to act legally, without fear of compromising their secrets.

Where is Waldo? [Naor]

Completeness Theorem [Yao, Goldreich –Micali –Wigderson]: Computational 1. More than 1/2 are honest Cryptographic 2. Players computationally bounded 3. Trap-door functions exist (e. g. factoring integers is hard) Every game, with any secrecy requirements, can be digitally implemented s. t. no collusion of the bad players can affect: * correctness (rules, outcome) * privacy (no information leaks) Theorem [Ben-Or –Goldwasser –Wigderson]: 1’. More than 2/3 are honest 2’. 3’. Private pairwise communication Informationtheoretic

Book ad - Published by Princeton University Press - Free (forever) on my website - Comments welcome!