Avi Wigderson Institute for Advanced Study Plan Proofs

Avi Wigderson Institute for Advanced Study

Plan Proofs and computations The value of errors in proofs: impact on Science: CS, Optimization, Coding… Technology: Crypto, Clouds, Blockchains, … Conceptual: Nature, paradoxical properties of proofs Math: Proof systems encode mathematical objects [JNVWY’ 20]: MIP* = RE The value of the complexity theory methodology Modelling, algorithmic efficiency, classification, …

Proofs and Computations Two points in a very long history [Euclid, 300 BC]: The Elements {Proofs of theorems in Plane Geometry, deducible from 5 simple axioms} = {Constructions of planar point sets using Straightedge and Compass}

Corollary: Computer revolution Polynomial time

Examples: claims, arguments, proof systems, provers, verifiers… What is true? In real life? In math? What is a convincing argument? Prover Verifier argument - Infinitely clever - Cannot be trusted - Eager to know - Limited

Volume comparison Claim: Left > Right Verification: General Algorithm Fill Left with water (to the rim) and pour to Right [if spills, ACCEPT, else, REJECT]

Composite numbers Claim: 147573952588676412927 composite Argument: 193707721, 761838257287 Crypto rests on the difficulty of finding such Verification: Check if General 193707721 x 761838257287 = 147573952588676412927 ACCEPT/REJECT Efficient algorithm: simple arithmetic Theorems = {Composite numbers}

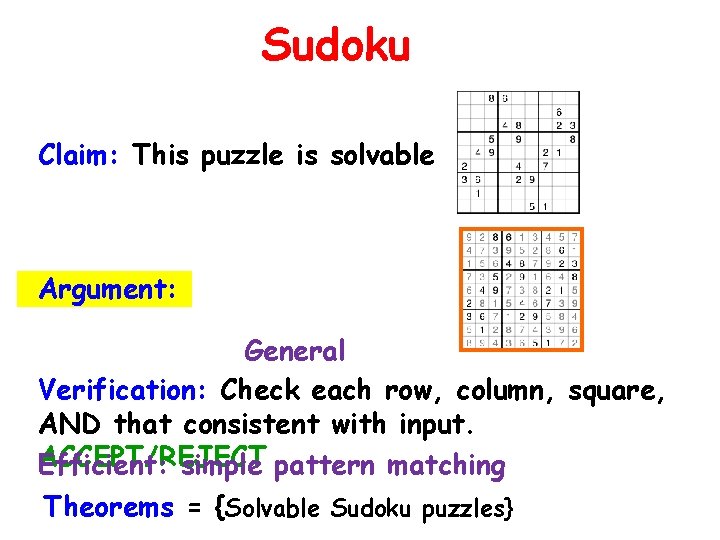
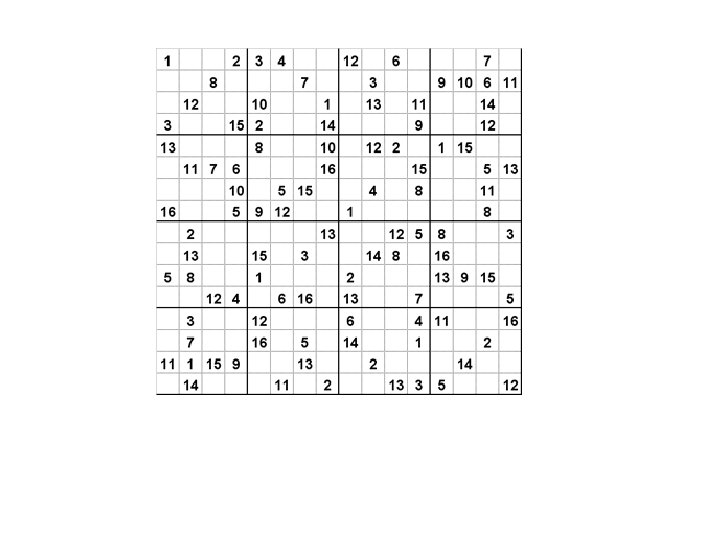
Sudoku Claim: This puzzle is solvable Argument: General Verification: Check each row, column, square, AND that consistent with input. ACCEPT/REJECT Efficient: simple pattern matching Theorems = {Solvable Sudoku puzzles}

Deductive proof systems e. g. Peano Arithmetic Numerous others Objects: Formulas/expressions over integers (A, B, . . ) Axioms: E. g. - x+y = y+x - x+1 > x - (x+y)z = xz+yz - Induction Principle Deduction rules: E. g. if A, A B true, then B is true. Argument (for claim C): A 1, A 2, …, Am = C Verification: Check that each Ai is an axiom, or follows from previous ones by a deduction rule. ACCEPT/REJECT Theorems: - There are infinitely many primes

Essentials of proof systems Completeness: True claims have proofs Soundness: False claims don’t Easy to check: Distinguishing convincing and faulty arguments by an efficient Verifier algorithm Time=poly(|claim|) A complexity theoretic view

Proof System • [Cook-Reckhow ’ 79]

Probabilistic computation & errors in algs

Probabilistic Proof System [Babai ‘ 85, Goldwasser-Micali-Rackoff ‘ 85] • probabilistic always WHP errors in proofs

IP = (Probabilistic) Interactive Proofs [Babai’ 85, Goldwasser-Micali-Rackoff’ 85] claim Prover NP Prover IP Reasonable argument q 1 a 1 …… qr ar Verifier (deterministic) ACC/REJ correctly always Verifier (probabilistic) A revolutionary scientific ACC/REJ correctly WHP

Value of errors in proofs: Impact of interactive proofs Conceptual, Mathematical, Scientific, Technological, … Proof with paradoxical properties ZK: Convincing proofs need not convey information PCP: Convincing proofs need only be glanced at The meandering journey from ZK to PCP and from IP to MIP*

ZKIP: Zero-Knowledge Interactive Proofs [Goldwasser-Micali-Rackoff ’ 85] claim ZKIP Formal def non-trivial! Prover q 1 a 1 …… qr Verifier ar Possible? Can a convincing proof be uninformative? ZKIP = IP + V ACC. V learns nothing else

Copyrights Dr. Alice: I can prove Riemann’s Hypothesis Prof. Bob: Impossible! What is the proof? Dr. Alice: Lemma…Proof…Lemma…Proof. . . Prof. Bob: Amazing!! I’ll recommend tenure Amazing!! I’ll publish first

ZKIP: Zero-Knowledge Interactive Proofs [Goldwasser-Micali-Rackoff ’ 85] claim ZKIP Formal def non-trivial! Prover q 1 a 1 …… qr Verifier ZKIP = IP + V ACC. V learns nothing else ar Possible? Can a convincing proof be uninformative? [Goldreich-Micali-Wigderson ’ 86] 1 -way functions exist NP ZKIP Every proof can be made into a ZK proof!

ZK impacts Theory: [Goldreich-Micali-Wigderson ’ 87, …] Automating secure cryptographic protocol design Practical applications: Anonymous cash, Blockchains, Public ledgers … Physical ZK proofs: [Barak-Glaser-Goldstone’ 14] Nuclear disarmament [Fisch-Freund-Naor ’ 14] Anonymous DNA testing, … New proof systems: MIP: allowing multiple provers

ZKIP: Zero-Knowledge Interactive Proofs [Goldwasser-Micali-Rackoff ’ 85] claim ZKIP Formal def non-trivial! Prover q 1 a 1 …… qr Verifier ar ZKIP = IP + V ACC. V learns nothing else [Goldreich-Micali-Wigderson ’ 86] 1 -way functions exist NP ZKIP Every proof can be made into a ZK proof! Crypto is used! Is it necessary?

2 IP: 2 -Prover Interactive Proofs (& MIP) [Ben. Or-Goldwasser-Kilian-Wigderson ‘ 89] claim 2 IP Reasonable? Prover 1 Socrates q 1 a 1 …… qr ar Verifier p 1 b 1 …… pr Correctly ACC/REJ WHP [BGKW ‘ 89] NP ZK 2 IP Physical separation replaces computational assumptions br Prover 2 Plato

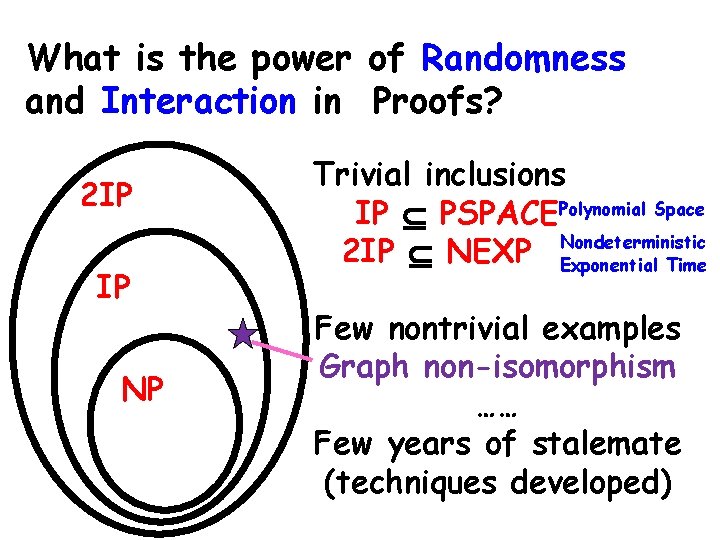
What is the power of Randomness and Interaction in Proofs? 2 IP IP NP Trivial inclusions IP PSPACEPolynomial Space Nondeterministic 2 IP NEXP Exponential Time Few nontrivial examples Graph non-isomorphism …… Few years of stalemate (techniques developed)

Avalanche of Characterizations + Conceptual meaning [Lund-Fortnow-Karloff-Nisan, Shamir ’ 90] PSPACE Winning strategies are efficiently verifiable! IP = [Babai-Fortnow-Lund ’ 91] 2 IP = NEXP Intractable problems are efficiently verifiable! Exponentially long arguments convince efficient verifiers! [Arora-Lund-Motwani-Safra-Sudan-Szegedy’ 92] PCP = No NP

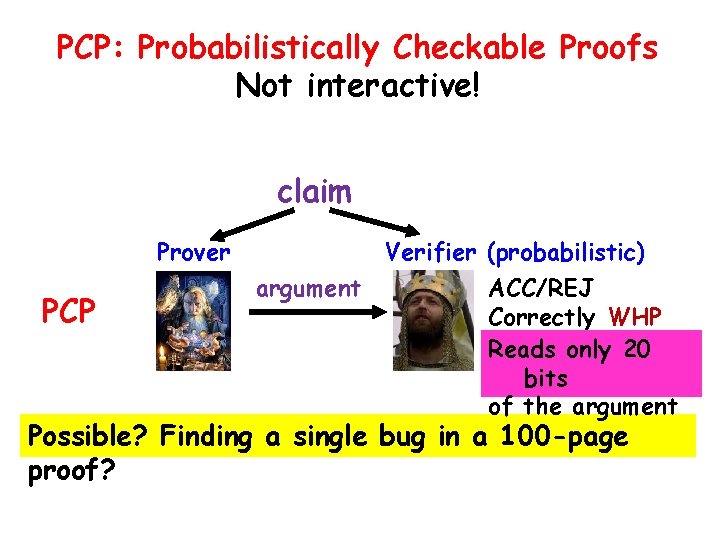
PCP: Probabilistically Checkable Proofs Not interactive! claim Prover PCP Verifier (probabilistic) argument ACC/REJ Correctly WHP Reads only 20 bits of the argument Possible? Finding a single bug in a 100 -page proof?

PCP (Probabilistically Checkable Proofs) Riemannclaim Hypothesis Prover Verifier (probabilistic) argument ACC/REJ NP=PCP Correctly WHP Reads only 20 bits the argument Possible? Finding a single bug in aof 100 -page proof? proof can be efficiently turned into a Every PCP! Refereeing in a jiffy Optimization Hardness of approximation Coding theory Complexity theory, … Technology cloud computing, blockchains, …

Back to Probabilistic Interactive Proofs Quantum [Lund-Fortnow-Karloff-Nisan, Shamir ’ 90] IP = PSPACE [Babai-Fortnow-Lund ’ 91] 2 IP = NEXP

Quantum computation

Quantum proof systems EPR controversy of quantum mechanics, Bell Inequalities, power of entanglement, …

MIP: Multi-Prover Interactive Proofs [BGKW ‘ 89] 2 IP Prover 1 Socrates claim q 1 a 1 q 1 …… qar 1 ar Verifier p 1 b 1 ……q 2 pr a 2 br Correctly ACC/REJ WHP Prover 2 Plato [Feige-Lovasz ‘ 92] MIP = 2 IP (1 round suffices).

1 -round 2 IP as Games [Cai-Condon-Lipton claim’ 90] Local 2 IP game Prover 1 q 1 a 1 Verifier q 2 a 2 Prover 2 Correctly ACC/REJ WHP Unchanged if provers share a random string Approximate val(G): Optimization problem

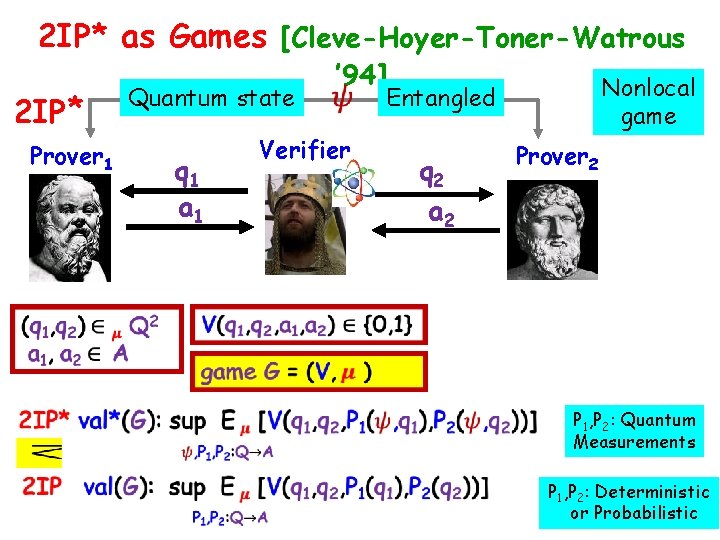
2 IP* as Games [Cleve-Hoyer-Toner-Watrous 2 IP* Prover 1 Quantum state q 1 a 1 ’ 94] Verifier Nonlocal game Entangled q 2 a 2 Prover 2 P 1, P 2: Quantum Measurements P 1, P 2: Deterministic or Probabilistic

The cool EPR game [Einstein-Podolski-Rosen’ 35 (IAS), Bohm’ 51, Bell ‘ 64, Clauser-Horne-Shimony-Holt ’ 67] Is quantum mechanics complete? val(EPR) = 3/4

[Ji-Natarajan-Vidick-Wright-Yuen’ 20] MIP* = RE

Book ad - Published by Princeton University Press - Free (forever) on my website - Comments welcome!