Programme M Sc Chemistry Session 2019 2021 SemesterII

Programme : M. Sc. Chemistry, Session: 2019 -2021, Semester-II Course Title: Quantum Mechanics II and Statistical Thermodynamics Course Code: MSCHE 2003 C 04 Rotation in 3 D: Particle on a Sphere Dr. Amiya Priyam Associate Professor Department of Chemistry Central University of South Bihar Gaya-824236

Rotation in two dimensions: the particle on a ring Two solutions of the Schrödinger equation for a particle on a ring. The circumference has been opened out into a straight line; the points at φ = 0 and 2π are identical. Ø The solution in (a) is unacceptable because it is not single-valued. Moreover, onsuccessive circuits it interferes destructively with itself, and does not survive. Ø The solution in (b) is acceptable: it is single-valued, and on

Rotation in two dimensions: the particle on a ring Ø The angular momentum of a particle confined to a plane can be represented by a vector of length |ml | units along the z-axis and with an orientation that indicates the direction of motion of the particle. The direction is given by the righthand screw rule.

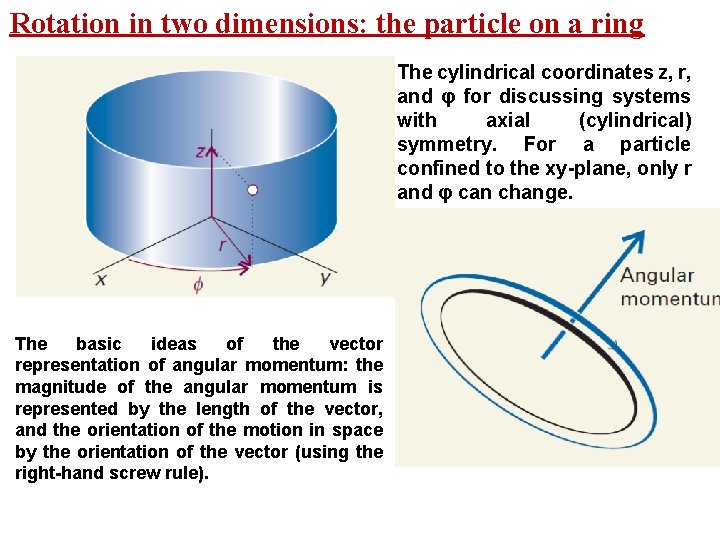
Rotation in two dimensions: the particle on a ring The cylindrical coordinates z, r, and φ for discussing systems with axial (cylindrical) symmetry. For a particle confined to the xy-plane, only r and φ can change. The basic ideas of the vector representation of angular momentum: the magnitude of the angular momentum is represented by the length of the vector, and the orientation of the motion in space by the orientation of the vector (using the right-hand screw rule).

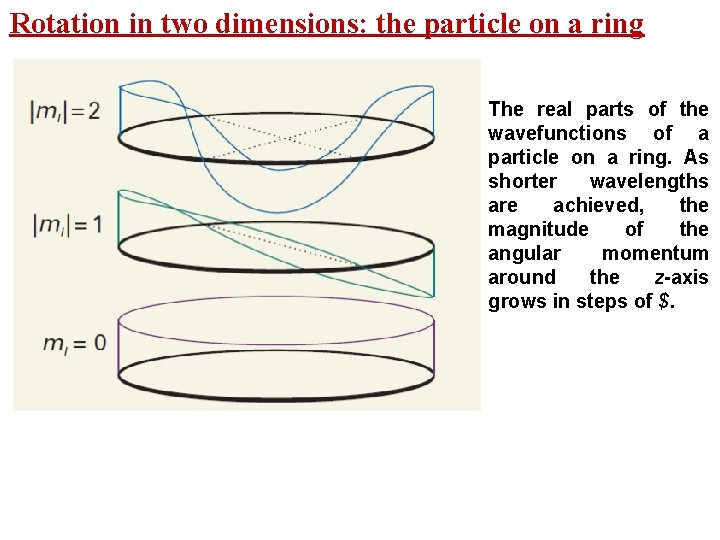
Rotation in two dimensions: the particle on a ring The real parts of the wavefunctions of a particle on a ring. As shorter wavelengths are achieved, the magnitude of the angular momentum around the z-axis grows in steps of $.

Rotation in three dimensions: the particle on a sphere Ø We now consider a particle of mass m that is free to moveanywhere on the surface of a sphere of radius r. Ø We shall build on the work we have already done on the particle on a ring. Ø A sphere can be thought of as a three-dimensional stack of rings with the additional freedom for the particle to migrate from one ring to another. Ø The cyclic boundary condition for the particle on a ring will once again lead to a quantum number, the match same as ml athat Ø However, the requirement that the wavefunction should pathwe is traced over the poles as well as round the equator of the sphere surrounding have already encountered. the central point introduces a second cyclic boundary condition and therefore a second quantum number

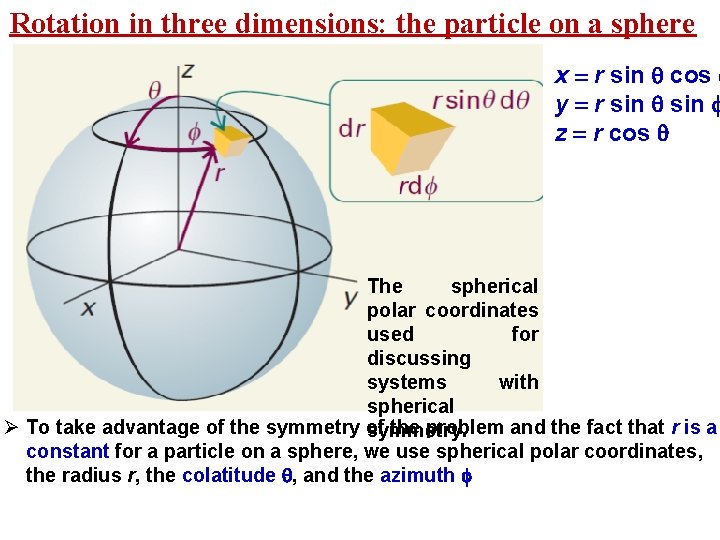
Rotation in three dimensions: the particle on a sphere x = r sin cos y = r sin z = r cos The spherical polar coordinates used for discussing systems with spherical Ø To take advantage of the symmetry of the problem and the fact that r is a symmetry. constant for a particle on a sphere, we use spherical polar coordinates, the radius r, the colatitude , and the azimuth

The Schrödinger equation for the particle on a sphere The Hamiltonian operator for motion in three dimensions Ø The sphere is treated as a three-dimensional stack of rings with the additional freedom for the particle to migrate from one ring to another. Therefore the solutions ca be written as where is a function only of , and , a function only of , is the solution for a particle on a ring.

The Schrödinger equation for the particle on a sphere Laplacian in spherical polar coordinates Is where the Legendrian, 2, is

Mathematical relations for transformation of coordinates

The Schrödinger equation for the particle on a sphere Omit this Because r is constant, we can discard the part of the Laplacian that involves differentiation with respect to r, and so write the Schrödinger equation as The moment of inertia, I = mr 2, has appeared. This expression can be rearranged into

The Schrödinger equation for the particle on a sphere To verify that this expression is separable, we try the substitution = with the form of the Legendrian We now use the fact that and are each functions of one variable, so the partial derivatives become complete derivatives: Division through by , multiplication by sin 2θ, and minor rearrangement give

The Schrödinger equation for the particle on a sphere Depends on only Ø The first term on the left is independent of , so if is varied only the second and third term of the three on the left can change. Ø But the sum of these three terms is a constant given by the right-hand side of the equation; therefore, if the second term did change then the right-hand side could not be constant. Ø Consequently, even the second term cannot change when is changed. In other words, the second term is a constant, which we write as m l 2. Ø By a similar argument, the first term is a constant when changes, and we write it as − ml 2

Rotation in three dimensions: the particle on a sphere Ø The first of these two equations is the same as that for particle on a ring so— as we anticipated—it has the same solutions. Ø The second equation is new, but its solutions are well known to mathematicians as ‘associated Legendre functions’. The surface of a sphere is covered by allowing to range from 0 to , and then sweeping that arc around a complete circle by allowing to range from 0 to Ø The cyclic boundary condition for the matching of the wavefunction at = 0 and 2 restricts ml to positive and negative integer values (including 0), as for a particle on a ring.

Rotation in three dimensions: the particle on a sphere Ø The additional requirement that the wavefunction also match on a journey over the poles results in the introduction of a second quantum number, l, with nonnegative integer values. Ø However, the presence of the quantum number ml in the second equation implies that the ranges of the two quantum numbers are linked, and it turns out that l can take the values 0, 1, 2, . . . and, for a given value of l, The surface of a sphere is Ø ml ranges in integer steps from -l to +l, covered by allowing to range from 0 to , and then sweeping that arc around a complete circle by allowing to range from 0 to

Rotation in three dimensions: the particle on a sphere Ø The normalized wavefunctions ψ(θ, φ) for a given l and ml are usually denoted Yl, ml(θ, φ) and are called the spherical harmonics Ø They are as fundamental to the description of waves on spherical surfaces as the harmonic (sine and cosine) functions are to the description of waves on lines and planes.

Rotation in three dimensions: the particle on a sphere The wavefunctions of a particle on the surface of a sphere that emphasizes the location of angular nodes: dark and light shading correspond to different signs of the wavefunction. Note that the number of nodes increases as the value of l increases. All these wavefunctions correspond to ml = 0; a path round the vertical zaxis of the sphere does not cut through any nodes.

Rotation in three dimensions: the particle on a sphere Ø There are no angular nodes (the positions at which the wavefunction passes through zero) around the z-axis for functions with ml = 0. Ø The spherical harmonic with l = 0, ml = 0 has no nodes at all: it is a ‘wave’ of constant height at all positions of the surface. Ø The spherical harmonic with l = 1, ml = 0 has a single angular q In general, the number of angular nodes is equal to l. node at θ = π/2; therefore, the equatorial plane is a nodal plane. The spherical harmonic l = 2, ml = 0 has two increases, the wavefunctions become more Ø with As the number of nodes angular nodes buckled, and with this increasing curvature we can anticipate that the kinetic energy of the particle increases Ø The energy of the particle is given by

Rotation in three dimensions: the particle on a sphere Ø Because there are 2 l + 1 different wavefunctions (one for each value of ml) that correspond to the same energy, it follows that a level with quantum number l is (2 l + 1)-fold degenerate. Ø Notice also that there is no zero-point energy because the groundstate (l = 0, ml = 0) wavefunction has a constant value and all its derivatives are zero. Ø The appearance of the factor l(l + 1) in eqn has its roots in the properties of the angular momentum operator, in particular the operator for the square of the magnitude of the angular momentum,

Rotation in three dimensions: the particle on a sphere • The number of nodes in Yl, ml (θ, φ) increases with l. It shows that higher angular momentum implies higher kinetic energy, and therefore a more sharply buckled wavefunction.

Space Quantization The permitted orientations of angular momentum when l = 2. We shall see soon that this representation is too specific because the azimuthal orientation of the vector (its angle around z) is indeterminate.