Presentation on Introduction to Groups Dr K SUVARNA
























- Slides: 24


Presentation on Introduction to Groups . Dr. K. SUVARNA Lecturer in Mathematics III Sem, Abstract Algebra D. K. Govt. college for women(A) Nellore. Ph : 9985039953

� The study of Algebraic Structures which have been subjected to Axiomatic development is called “Abstract Algebra or Group Theory”. � Basic ingredients of Group Theory are Sets, Relations and Mappings. �A set with a method of combination of elements of it called an Algebraic structure.

Binary operation : � Let s be a non-empty set If f : sxs →s is a mapping then f is called “Binary operation” in S or “Binary composition” in S. i. e. , (a , b) є SXS => f(a , b) є S i. e. , a є S , b є S => a. b є S then ‘. ’ is called a “Binary operation” in the set S. which is known as “Closure law”. Ex: Let N be the set of Natural numbers and for any a є N , b є N if a + b є N then ‘+’ is the binary operation in N.

� For any two natural numbers (>0) 4, 8 є N We have 4+8=12 є N then “+” is a binary operation in N whereas “-” is not a binary operation in N since for any two numbers 6, 12 є N we have 6 -12 = -6 does not belongs to N. i. e “-”’ is not a binary operation in N as (a, b) є N does not imply a-b є N.

ASSOCIATIVE LAW ‘*’ is a binary operation in S , for any a, b, c є S if (a*b)*c = a*(b*c) then the operation “*” is called ASSOCIATIVE in ‘S’. c=3 Ex: a, b, c є Z a+(b + c) = (a + b)+c let us take a=1, b=2, 1+(2+3)= (1+2)+3 1+5= 3+3 6=6

Existence of Identity : � In a non-empty set G for any aєG there exist e єG Э a*e = e*a = a then ‘e’ is called an Identity element in G w. r. to the operation “*”. → With respect to addition ‘ 0’ is the identity element since 0+a = a+0 = a. Ex : for any number -6 є Z there exists 0 є Z such that -6 + 0 = 0+ (-6) = -6 � Ex : 3+0 = 0+3 = 3 → Under multiplication ‘ 1’ is the identity element

Inverse property : For any a є G there exists b є G Э a*b = b*a = e then ‘b’ is called Inverse element of ‘a’ in G. → Under addition inverse of a is –a → Under multiplication inverse of a is 1/a Ex : for 3є Z there exists -3 є Z Э 3+ (-3) = -3 + 3 = 0

Algebraic structure A non-empty set G equipped with one or more binary operations is called Algebraic structure. Ex: (R, . , +), (Z, . )

Semi Group An Algebraic structure which is Associative is called Semi group Ex: (N, +) is Semi group i. e, For a, b, c ЄN 1. aєN, bєN =>a + b є N 2. (a + b)+c = a+(b + c)

Monoid A Semi group with the identity element is known as “Monoid”. i. e. , (S, 0) is a Monoid if a non-empty S under the operation “ 0” follows 1. Binary operation (or) Closure law 2. Associativity 3. Identity Ex: 1. (N, +) is not a monoid since 0 does not є N 2. (R, +) , (N, . ) , (Z, +) are the monoids. .

Group Let G be a non empty set and ‘*’ is a binary operation defined on G then (G, *) is said to be a Group if it satisfies the following properties 1. Associative property 2. Identity property and 3. Inverse property Ex : (Z, +), (R, +), (Q, +) etc are groups under “+”.

ABELIAN GROUP In a group (G, 0) If a, b є G => a 0 b = b 0 a then (G, 0) is called an “Abelian or Commitative group”. Ex: (Z, +), (R, +), (C, +), (Q, +) are the Commitative groups.

FINITE AND INFINITE GROUP In group (G, 0) If the number of the elements are finite then it is called “Finite group”. Otherwise it is “Infinite group”. Ex: (R, +), (Z, +), (Q, +)

ORDER OF A GROUP The number of elements in a group (G, 0) is called it’s “order”. And it is denoted by 0(G) < ∞. Ex: 0(G) = 2 n for all n є Z is the group of even order. 0(G) = 2 n-1 for all n є N is the group of the odd order.

Any subset H of a group G is called a Complex. Ex: Set of all even integers is complex of group (Z, +) Ex 2: In the Group, fourth roots of unity {1, -1, i, -i }, the complexes are {1, -1}, {i, -i}, ……

If a complex H of a group G is itself a group under the operation of G, we say that H is a Subgroup of G denoted by H≤G Ex: (Z, +) is the subgroup of (Q, +) (R, +) is the subgroup of (C, +)

If a complex H of a group G is itself a group under the operation of G, we say that H is a Subgroup of G denoted by H≤G Ex: (Z, +) is the subgroup of (Q, +) If +) (R, +) is the subgroup of (C,

The fourth roots of unity {1, -1, i, -i} is the group G under multiplication. The complex {1, -1} is a subgroup but {i, -i} is not a subgroup WHY?

Criteria of a subset to be a subgroup: Theorem: H is a non-empty complex of a subgroup G, the necessary and sufficient condition for H to be a subgroup of G is a, b ϵ H =>ab^(-1) ϵ H In additive notation, H is a subgroup of G iff a, b ϵ H => a-b ϵ H

Two-Step Subgroup Test Theorem: A non-empty complex H of a group G is a subgroup 1) a ϵ H, b ϵ H => ab ϵ H. 2) a ϵ H => a^(-1) ϵ H.

Finite Subgroup Test Theorem: Let H be a non-empty finite complex of a group G. If H is closed under the operation of G, then H is a subgroup of G. i. e. a, b ϵ H => ab ϵ H.

Some Other Criterions A necessary and sufficient condition for a non-empty complex H of a subgroup G to be a subgroup of G is that HH^(-1) is contained in H. A necessary and sufficient condition for a non-empty subset H of a subgroup G to be a subgroup of G is that HH^(-1) = H.

THANK YOU
 Suvarna arogya suraksha trust
Suvarna arogya suraksha trust Dr suvarna khadilkar
Dr suvarna khadilkar Suvarna arogya suraksha trust hospital list
Suvarna arogya suraksha trust hospital list How are ethnic groups and religious groups related
How are ethnic groups and religious groups related Diameters of fetal head
Diameters of fetal head Cephalic presentation
Cephalic presentation Purpose of presentation
Purpose of presentation Presentation introduction example
Presentation introduction example Introduction for presentation
Introduction for presentation Conclusion of seminar presentation
Conclusion of seminar presentation Short oral presentation example
Short oral presentation example Introduction to mental health awareness presentation
Introduction to mental health awareness presentation Presentation conclusion phrases
Presentation conclusion phrases Presentation skills introduction
Presentation skills introduction Case study nuclear medicine
Case study nuclear medicine That's all for our presentation
That's all for our presentation Introduction about food presentation
Introduction about food presentation Presentation introduction in english
Presentation introduction in english Introduction for presentation in college
Introduction for presentation in college Hospital introduction presentation
Hospital introduction presentation Teksun introduction presentation
Teksun introduction presentation Bffc11
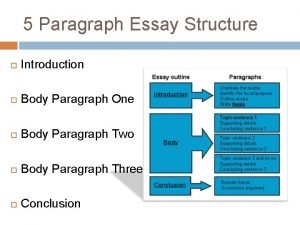
Bffc11 Body paragraph structure
Body paragraph structure Free word combinations examples
Free word combinations examples Mbti team building workshops
Mbti team building workshops