Power Series as Functions Defining our Function The

Power Series as Functions

Defining our Function The power series is a function on its interval of convergence. That is, if the series converges at x = c, then define is a number and we can In general, we can say that

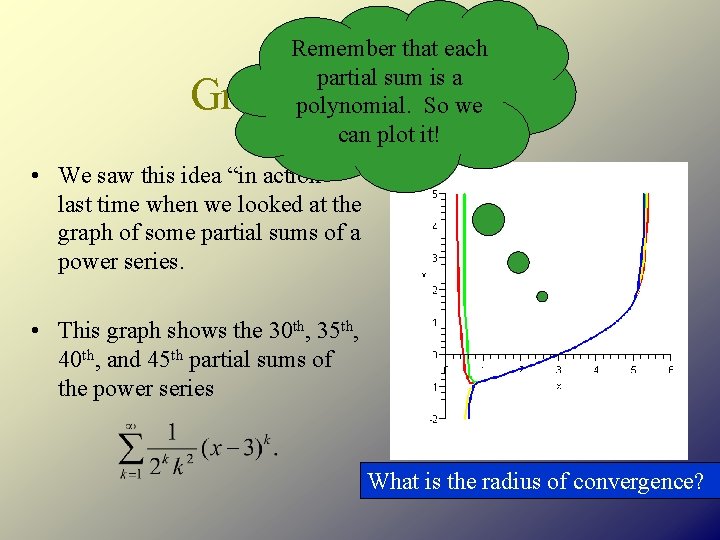
Remember that each partial sum is a polynomial. So we can plot it! Graphical Example • We saw this idea “in action” last time when we looked at the graph of some partial sums of a power series. • This graph shows the 30 th, 35 th, 40 th, and 45 th partial sums of the power series What is the radius of convergence?

Some Questions Arise Suppose that we consider the sorts of functions that are sums of Power Series: • What are these functions like? • Can we find formulas for them? • Are power series functions continuous? Are they differentiable? • If so, what do their derivatives and antiderivatives look like?

Consider an (already familiar) Example You guessed it. . . It’s our old friend the geometric series! We know it converges to and diverges elsewhere. That is, whenever |x| < 1

Our first formula! We see the expected convergence on a “balanced” interval about x = 0. Near x = 1, the partial sums “blow up” giving us the asymptote we expect to see there. This plot shows the 10 th, 12 th, 13 th, and 15 th partial sums of this series. Near x = -1 the even and odd partial sums go opposite directions, preventing any convergence to the left of x = -1.

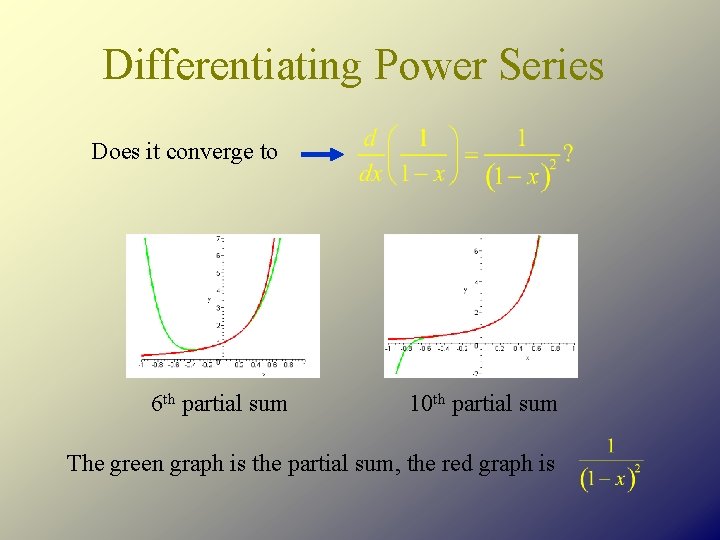
Our first formula! What else can we observe? Clearly this function is both continuous and differentiable on its interval of convergence. It is very tempting to say that the derivative for f (x) = 1 + x 2 + x 3 +. . . should be But is it? For that matter, does this series even converge? And if it does converge, what does it converge to?

It does converge, as the ratio test easily shows: The general form of the series is So the ratio test limit is: So the “derivative” series also converges on (-1, 1). What about the endpoints? Does it converge at x = 1? x = -1?

Differentiating Power Series Does it converge to 6 th partial sum 10 th partial sum The green graph is the partial sum, the red graph is

This is true in general: Theorem: (Derivatives and Antiderivatives of Power Series) Let be a power series with radius of convergence r > 0. And let and Then: • both D and A converge with radius of convergence r; • on the interval (x 0 - r, x 0+r), S’(x) = D(x); • on the interval (x 0 - r, x 0+r), A’(x) = S(x).

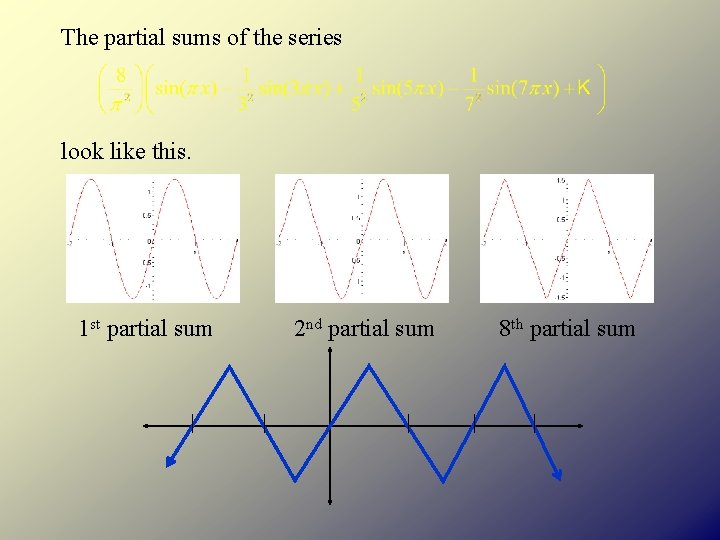
Is this true of all Series Functions? No. Power Series are very special in this regard! If, instead of adding up powers of x with coefficients, we add up trig functions, we get very different behavior. Consider, for example

The partial sums of the series look like this. 1 st partial sum 2 nd partial sum 8 th partial sum

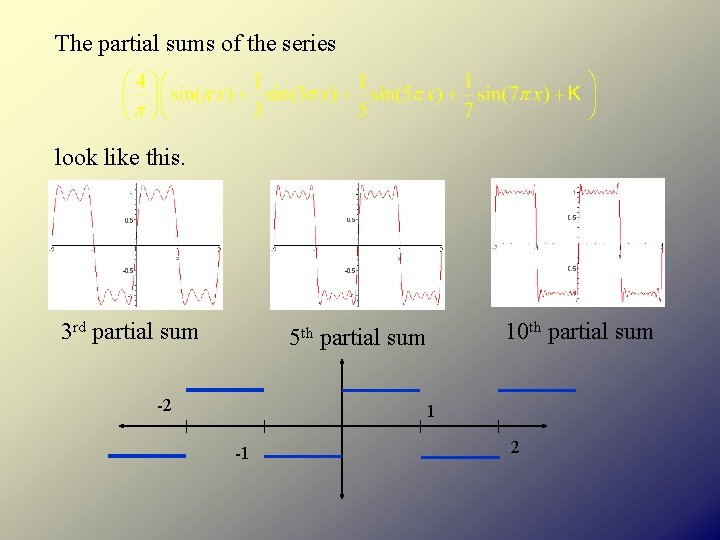
The partial sums of the series look like this. 3 rd partial sum 5 th -2 10 th partial sum 1 -1 2