Poisson Surface Reconstruction LIU Shishi YOU Qingfei WANG

Poisson Surface Reconstruction LIU Shishi YOU Qingfei WANG Wentao HONG Su

Outline n n n Introduction Mathematical modeling and related work Poisson reconstruction approach Implementation Analysis of Non-uniform Samples Results

Introduction n Reconstructing 3 D surfaces from point samples is a well studied problem in computer graphics.

Introduction n The key insight of Poisson surface reconstruction is that there is an integral relationship between oriented points sampled from the surface of a model and the indicator function of the model.

Mathematical modeling and related work n n In order to compute the indicator function, the most important is to invert the gradient operator. ——find the scalar function whose gradient best approximates a vector field defined by samples, shown as :

Mathematical modeling and related work n If we apply the divergence operator, this problem transforms to standard Poisson problem.

Poisson problem n n n In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics and theoretical physics. The Poisson equation is

Poisson reconstruction approach n 1 Defining the gradient field n 2 Approximating the gradient field n 3 Solving the Poisson problem

Poisson reconstruction approach n The input data S is a set of samples s, each consisting of a point s. p and an inward-facing normal s. N, assumed to lie on or near the surface of an unknown model M.

Defining the gradient field n Lemma:

Defining the gradient field

Implementation n Uniformly distributed samples n Non-uniformly distributed samples

Function Space n n n An adaptive octree to represent and solve the Poisson system Minimal octree Node function and base function

Base function n n Approximate a Gaussian with unit-variance A compactly supported function

Vector Field Definition n Use trilinear interpolation to distribute the sample across the eight nearest neighbour nodes

Poisson Solution(1) n Poisson Equation n Solving for function n o-th coordinate of |O| dimensional vector v minimizing:

Poisson Solution(2) • Matrix Form • Let then • Our problem is equal to finding x for

Isosurface Extraction Average value: Isosurface:

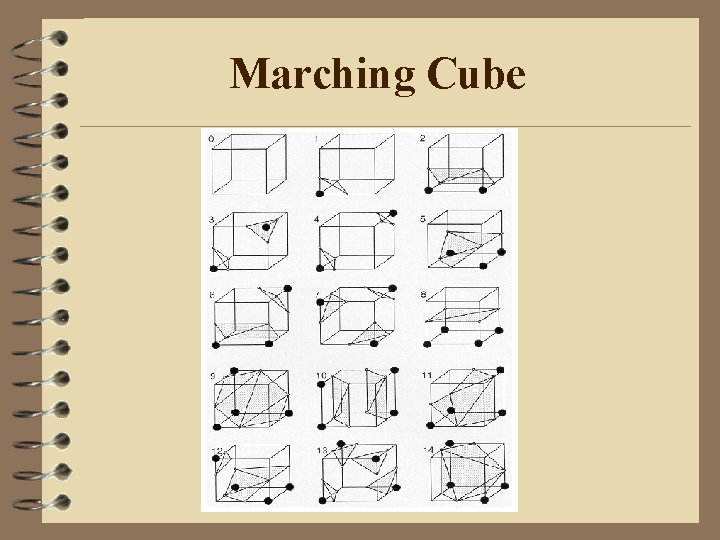
Marching Cube • The most common used way of face drawing. • Key point: find the intersection of one cube the indicator function. • Construct the triangle network in every cube, a divide-and-conquer approach.

Marching Cube

Marching Cube n Calculate the value of indicator function of 8 vertices. Inside or outside : 256 possibilities. p In fact, only 14 patterns are needed. p n Do the interpolation in the edge to find the point of surface. n Make the triangle.

Marching Cube n The problem is the crack p n the vertexes in the adjacent faces may have different ways of connection. The solution p if there are two or more “zero-crossing”, divide the node of cube.

Non-uniform Samples n “splatting” the points into the grid. n Estimate the density of sampling for modifiy our formula. p Expressed by the sum of the node function

Non-uniform Samples • Calculate the vector field with the weight of density. • The modified formula • Another problem in sparsely sampling region • • poor noise filtering Adapted the filter width to the local sampling density.

Non-uniform Samples The formula: In which,

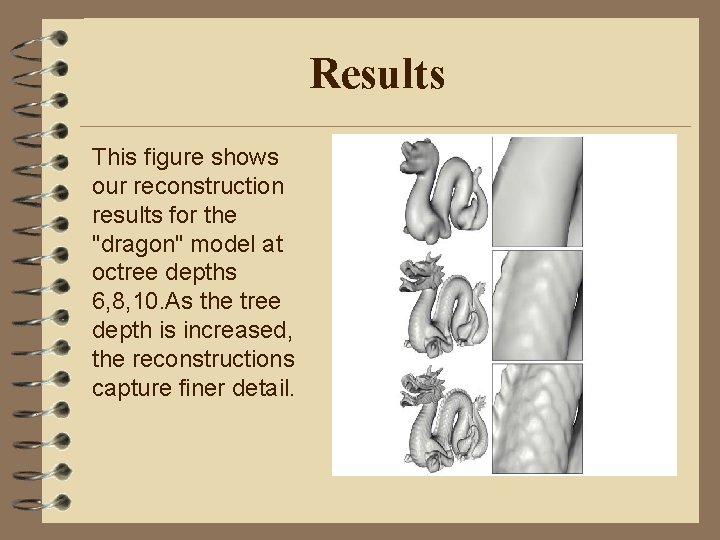
Results This figure shows our reconstruction results for the "dragon" model at octree depths 6, 8, 10. As the tree depth is increased, the reconstructions capture finer detail.