Pengantar Kecerdasan Buatan 4 Informed Search and Exploration

Pengantar Kecerdasan Buatan 4 - Informed Search and Exploration AIMA Ch. 3. 5 – 3. 6

2 Review : Tree Search • A search strategy is defined by picking the order of node expansion OSCAR KARNALIM, S. T. , M. T.

3 Best-first Search • Idea: use an evaluation function f(n) for each node estimate of "desirability" • Expand most desirable unexpanded node • • Implementation: • • Order the nodes in fringe in decreasing order of desirability Special cases: Greedy best-first search • A* search • OSCAR KARNALIM, S. T. , M. T.

4 Heuristic • Heuristic are criteria, methods , or principle for deciding among several course of action promises to be the most effective in order to reach some goal • h(n) = estimated cost of the cheapest path from node n to a goal node OSCAR KARNALIM, S. T. , M. T.

5 Greedy Best-first Search • Evaluation function f(n) = h(n) • Greedy best-first search expands the node that appears to be closest to goal • e. g. in Bucharest Problem, h. SLD(n) = straight-line distance from n to Bucharest OSCAR KARNALIM, S. T. , M. T.

6 Romania with Step Costs in KM OSCAR KARNALIM, S. T. , M. T.

7 Greedy Best-first Search Example OSCAR KARNALIM, S. T. , M. T.

8 Greedy Best-first Search Example (Cont) OSCAR KARNALIM, S. T. , M. T.

9 Greedy Best-first Search Example (Cont) OSCAR KARNALIM, S. T. , M. T.

10 Greedy Best-first Search Example (Cont) OSCAR KARNALIM, S. T. , M. T.

11 Properties of Greedy Best-first Search Complete? No – can get stuck in loops, e. g. , Iasi Neamt Time? O(bm), but a good heuristic can give dramatic improvement Space? O(bm) -- keeps all nodes in memory Optimal? No OSCAR KARNALIM, S. T. , M. T.

12 A* Search Idea: avoid expanding paths that are already expensive Evaluation function f(n) = g(n) + h(n) g(n) = cost so far to reach n h(n) = estimated cost from n to goal f(n) = estimated total cost of path through n to goal OSCAR KARNALIM, S. T. , M. T.

13 A* Search Example OSCAR KARNALIM, S. T. , M. T.

14 A* Search Example (Cont) OSCAR KARNALIM, S. T. , M. T.

15 A* Search Example (Cont) OSCAR KARNALIM, S. T. , M. T.

16 A* Search Example (Cont) OSCAR KARNALIM, S. T. , M. T.

17 A* Search Example (Cont) OSCAR KARNALIM, S. T. , M. T.

18 A* Search Example (Cont) OSCAR KARNALIM, S. T. , M. T.

19 Admissible Heuristics A heuristic h(n) is admissible if for every node n, h(n) ≤ h*(n), where h*(n) is the true cost to reach the goal state from n. An admissible heuristic never overestimates the cost to reach the goal, i. e. , it is optimistic Example: h. SLD(n) (never overestimates the actual road distance) Theorem: If h(n) is admissible, A* using TREE-SEARCH is optimal OSCAR KARNALIM, S. T. , M. T.

20 Consistent Heuristics A heuristic is consistent if for every node n, every successor n' of n generated by any action a, h(n) ≤ c(n, a, n') + h(n') Theorem: If h(n) is consistent, A* using GRAPH-SEARCH is optimal OSCAR KARNALIM, S. T. , M. T.

21 Properties of A* • Complete? Yes • Time? Exponential • Space? Keeps all nodes in memory • Optimal? Yes OSCAR KARNALIM, S. T. , M. T.

22 Iterative-deepening A* (IDA*) • Adapt the idea of iterative deepening to the heuristic search context • The main difference between IDA* and standard iterative deepening is that the cutoff used is the f -cost (g + h) rather than the depth • The cutoff value is the smallest f -cost of any node that exceeded the cutoff on the previous iteration OSCAR KARNALIM, S. T. , M. T.

23 Properties of IDA* • Complete? Yes • Time? DFS • Space? DFS • Optimal? Yes OSCAR KARNALIM, S. T. , M. T.

24 Recursive best-first search (RBFS) • Simple recursive algorithm that attempts to mimic the operation of standard best-first search, but using only linear space • Its structure is similar to that of a recursive DFS, but rather than continuing indefinitely down the current path, it keeps track of the f-value of the best alternative path available from any ancestor of the current node OSCAR KARNALIM, S. T. , M. T.

25 Recursive best-first search (RBFS) (Cont) • If the current node exceeds this limit, the recursion unwinds back to the alternative path • As the recursion unwinds, RBFS replaces the f -value of each node along the path with the best f -value of its children • In this way, RBFS remembers the f -value of the best leaf in the forgotten subtree and can therefore decide whether it's worth reexpanding the subtree at some later time OSCAR KARNALIM, S. T. , M. T.

26 RBFS search for the shortest route to Bucharest • The path via Rimnicu Vilcea is followed until the current best leaf (Pitesti) has a value that is worse than the best alternative path (Fagaras) OSCAR KARNALIM, S. T. , M. T.

27 RBFS search for the shortest route to Bucharest (Cont) • The recursion unwinds and the best leaf value of the forgotten subtree (417) is backed up to Rimnicu Vilcea; then Fagaras is expanded, revealing a best leaf value of 450 OSCAR KARNALIM, S. T. , M. T.

28 RBFS search for the shortest route to Bucharest (Cont) • The recursion unwinds and the best leaf value of the forgotten subtree (450) is backed up to Fagaras; then Rirnnicu Vilcea is expanded • This time, because the best alternative path (through Timisoara) costs at least 447, the expansion continues to Bucharest OSCAR KARNALIM, S. T. , M. T.

29 Simplified Memory-bounded A* (SMA*) • SMA* proceeds just like A*, expanding the best leaf until memory is full • SMA* always drops the worst leaf node-the one with the highest f-value • SMA* then backs up the value of the forgotten node to its parent OSCAR KARNALIM, S. T. , M. T.

30 Simplified Memory-bounded A* (SMA*) (Cont) • In this way, the ancestor of a forgotten subtree knows the quality of the best path in that subtree • With this information, SMA* regenerates the subtree only when all other paths have been shown to look worse than the path it has forgotten OSCAR KARNALIM, S. T. , M. T.

31 Relaxed Problem A problem with fewer restrictions on the actions is called a relaxed problem The cost of an optimal solution to a relaxed problem is an admissible heuristic for the original problem OSCAR KARNALIM, S. T. , M. T.

32 Admissible Heuristics in 8 -Puzzle E. g. , for the 8 -puzzle: h 1(n) = number of misplaced tiles h 2(n) = total Manhattan distance (i. e. , no. of squares from desired location of each tile) h 1(S) = ? 8 h 2(S) = ? 3+1+2+2+2+3+3+2 = 18 Cost = 1 for each move of blank tile Alternatif PR-1: Diketahui bahwa kotak kosong bisa bergerak ke: atas, bawah, kiri atau kanan. Gunakan salah satu heuristik di samping untuk mencari kemungkinan langkah terbaik untuk mencapai goal dengan A*. Batasi ruang pencarian pada kedalaman 3. OSCAR KARNALIM, S. T. , M. T.

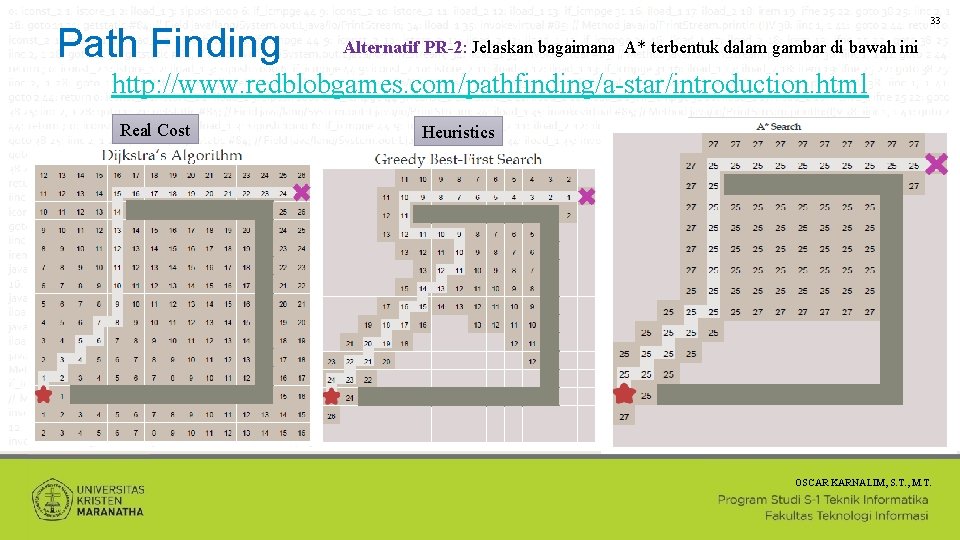
Path Finding 33 Alternatif PR-2: Jelaskan bagaimana A* terbentuk dalam gambar di bawah ini http: //www. redblobgames. com/pathfinding/a-star/introduction. html Real Cost Heuristics OSCAR KARNALIM, S. T. , M. T.