Organizacin de datos Estudiaremos cuatro formas de organizar

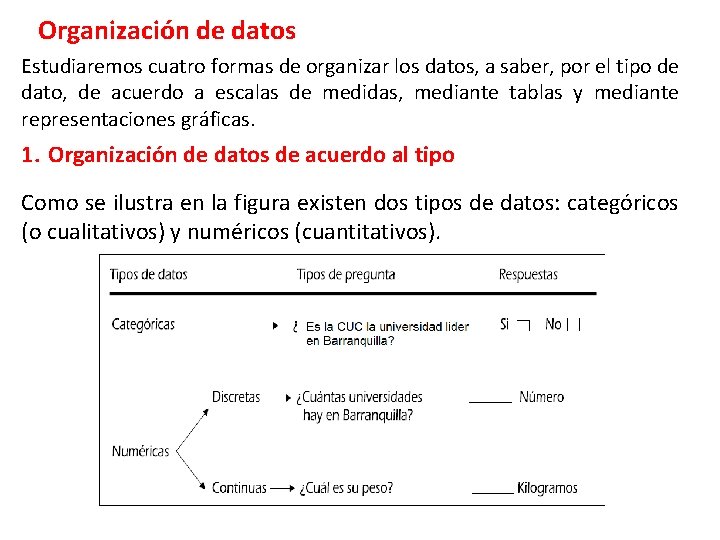
Organización de datos Estudiaremos cuatro formas de organizar los datos, a saber, por el tipo de dato, de acuerdo a escalas de medidas, mediante tablas y mediante representaciones gráficas. 1. Organización de datos de acuerdo al tipo Como se ilustra en la figura existen dos tipos de datos: categóricos (o cualitativos) y numéricos (cuantitativos).

1. Los datos categóricos o cualitativos representan categorías o atributos (como, por ejemplo, sí o no) que pueden clasificarse como un criterio o cualidad. 2. Los datos numéricos o cuantitativos producen respuestas numéricas como el peso en kilogramos o el número de universidades que hay en la Costa Atlántica. 3. Los datos discretos producen respuestas numéricas que surgen de un conteo. Ejemplos: La cantidad de universidades que hay en la Costa Atlántica, el número de estudiantes en la Universidad, la cantidad de hermanos que tiene un determinado estudiante de administración, el número de personas en una fila, etc.

Los datos continuos producen respuestas numéricas que surgen de un proceso de medición, donde la característica de que se mide puede tomar cualquier valor numérico en un intervalo. Ejemplos: El peso (en kilogramos) de una persona, su estatura (en metros), el tiempo que usted tarda en llegar a la Universidad. 2. Organización de datos de acuerdo a escalas de medidas Los datos también se pueden clasificar según la escala de medición o el procedimiento que los generó. Cuatro tipos de escalas de medición usados en estadística son las escalas nominal, ordinal, de intervalo y de razón. Datos de nivel nominal Un dato nominal se crea cuando se utilizan nombres para establecer categorías con la condición de que cada dato pertenezca única y exclusivamente a una de estas categorías. Existen escalas nominales tanto para los datos numéricos como categóricos. Una escala nominal para datos numéricos asigna números a las categorías. Una escala nominal para datos categóricos es un agrupamiento no ordenado de los datos en categorías discretas, donde cada dato puede incluirse solamente en uno de los grupos.

Datos de nivel ordinal Los datos medidos en una escala nominal ordenada de alguna manera se denominan datos ordinales. Una escala ordinal coloca las medidas en categorías, cada una de las cuales indica un nivel distinto respecto a un atributo que se está midiendo. La lista de datos ordinales comprende: 1. Clasificaciones por letra: A, B, C y D; estos grados indican categorías de perfeccionamiento, así como los niveles alcanzados. 2. Rangos académicos: Doctor, magister, especialista y licenciado. 3. La evaluación de un maestro: insuficiente, aceptable, bueno y excelente. 4. Los grados de la escuela: primero, segundo, tercero, etc. Datos de nivel de intervalo Los datos medidos en una escala ordinal para los cuales pueden clasificarse las distancias entre valores, se llaman datos de intervalos. La distancia entre dos valores es importante y los datos de intervalo son numéricos por necesidad; una escala de intervalo no siempre tiene un punto cero (es decir, un punto que indique la ausencia de lo que se quiere medir). La lista de datos de intervalo comprenden: 1. Puntajes en las pruebas de inteligencia. 2. Temperaturas Celsius. 3. Fechas.

3. Organización de datos mediante tablas En esta forma de organización de datos es importante el concepto de frecuencia de un dato. La frecuencia (absoluta) de un dato, simbolizado con la letra f, es el número de veces que aparece ese dato en una colección de datos. Ejemplo -En el conjunto de datos 4 5 5 3 2 6 7 7 7 2, el cuatro sólo aparece una vez (por lo tanto, tiene frecuencia f = 1), El cinco aparece dos veces (o sea, frecuencia f = 2), El 7 tiene frecuencia f = 3, etc.

Tabla de frecuencias no agrupadas Son aquellas en donde cada dato tiene la frecuencia correspondiente. La tabla de frecuencias (no agrupada) para el conjunto de datos 3 5 7 6 4 3 7 6 6 7 5 7 es

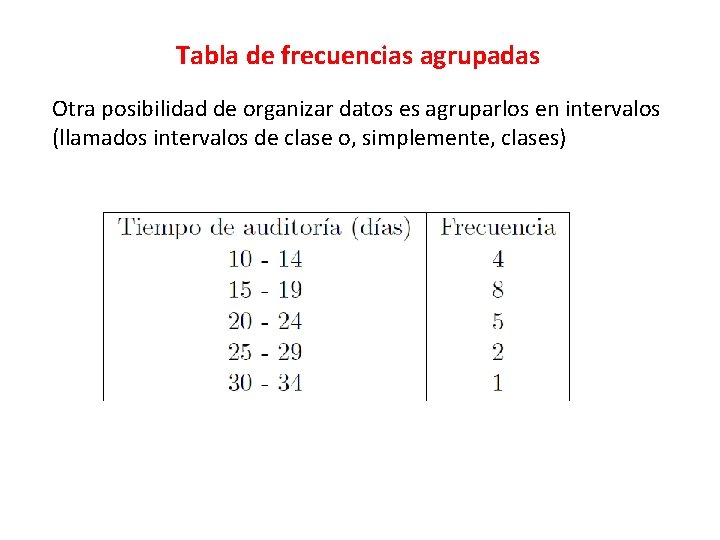
Tabla de frecuencias agrupadas Otra posibilidad de organizar datos es agruparlos en intervalos (llamados intervalos de clase o, simplemente, clases)

Las clases de frecuencias agrupadas poseen límites de clase. En la clase 10 -14, a 10 se le llama límite inferior de clase y a 14, límite superior de clase. La distancia entre cualquiera de dos límites superiores consecutivos o entre cualquiera de dos límites inferiores consecutivos es llamada amplitud de clase. La amplitud de cada clase en la tabla anterior es 5.

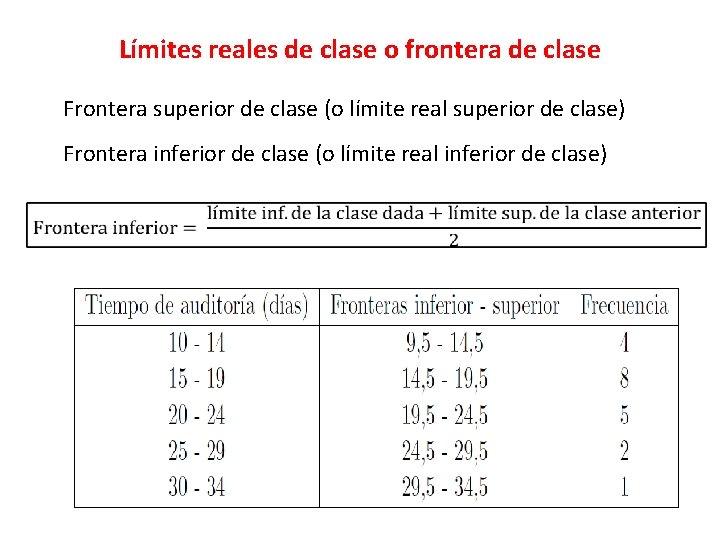
Límites reales de clase o frontera de clase Frontera superior de clase (o límite real superior de clase) Frontera inferior de clase (o límite real inferior de clase)

Sugerencias para construir una tabla de frecuencias agrupadas 1. En la realidad, se acostumbra siempre a agrupar los datos en clases en donde los extremos de la clase son las respectivas fronteras, en vez de los límites de clase. 2. Para mayor comodidad en el proceso de construcción de las clases, acordaremos que la primera clase debe contener por lo menos el dato menor (en la realidad, esto no siempre es así). 3. Las clases deben ser mutuamente excluyentes, es decir, cada dato debe quedar exactamente en una sola clase, no en dos al mismo tiempo. 4. Para mayor comodidad en el proceso de construcción de las clases, acordaremos que todas las clases deben tener la misma amplitud (en la realidad, esto no siempre es así). Determinación de la amplitud de clase. Réstense dos límites superiores de clases consecutivos o dos límites inferiores de clases consecutivos, o dos fronteras inferiores consecutivas, o dos fronteras superiores consecutivas, o réstese la frontera inferior de una clase de la frontera inferior superior de dicha clase.

6. Luego, determinar el rango R, que es la diferencia entre las medidas mayor y menor. 7. Posteriormente la amplitud de clase w se encuentra como se muestra en el siguiente recuadro.

8. El dato menor debe caer en la primera clase. Por esta razón, el límite inferior de la primera clase debe estar en, o un poco antes de, el dato menor. Así que podemos establecer un acuerdo general sobre las clases de nuestras tablas de frecuencias Ejercicio 10 Los datos anotados representan los totales, en miles de pesos, gastados en fotocopias por una muestra de 25 estudiantes durante un semestre. 29 89 77 72 39 47 64 84 88 57 28 63 38 42 36 72 69 68 41 52 39 84 45 52 72 Construya una tabla de frecuencias agrupadas usando la regla de Sturges. Solución Rango: R = Dato mayor – Dato menor = 89 – 28 = 61

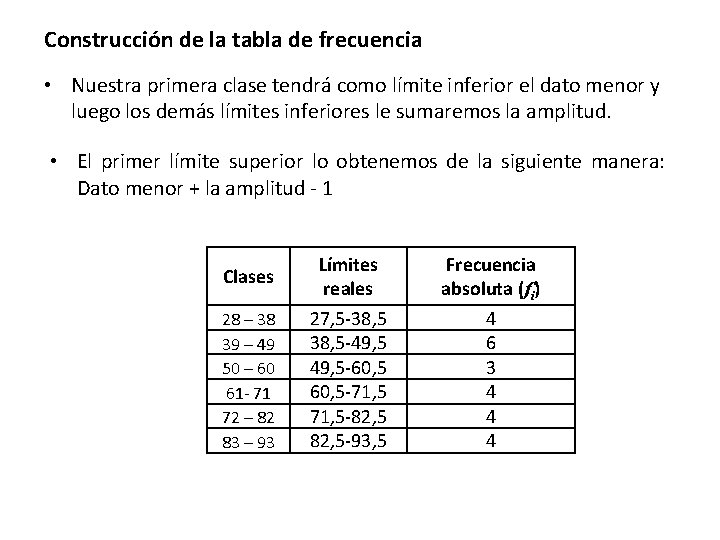
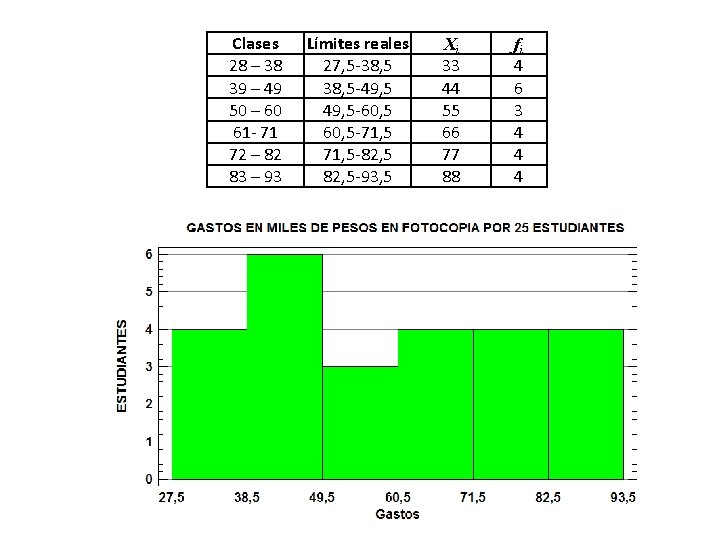
Construcción de la tabla de frecuencia • Nuestra primera clase tendrá como límite inferior el dato menor y luego los demás límites inferiores le sumaremos la amplitud. • El primer límite superior lo obtenemos de la siguiente manera: Dato menor + la amplitud - 1 Clases 28 – 38 39 – 49 50 – 60 61 - 71 72 – 82 83 – 93 Límites reales 27, 5 -38, 5 -49, 5 -60, 5 -71, 5 -82, 5 -93, 5 Frecuencia absoluta (fi) 4 6 3 4 4 4

Clases 28 – 38 39 – 49 50 – 60 61 - 71 72 – 82 83 – 93 Límites reales 27, 5 -38, 5 -49, 5 -60, 5 -71, 5 -82, 5 -93, 5 Xi 33 44 55 66 77 88 fi 4 6 3 4 4 4

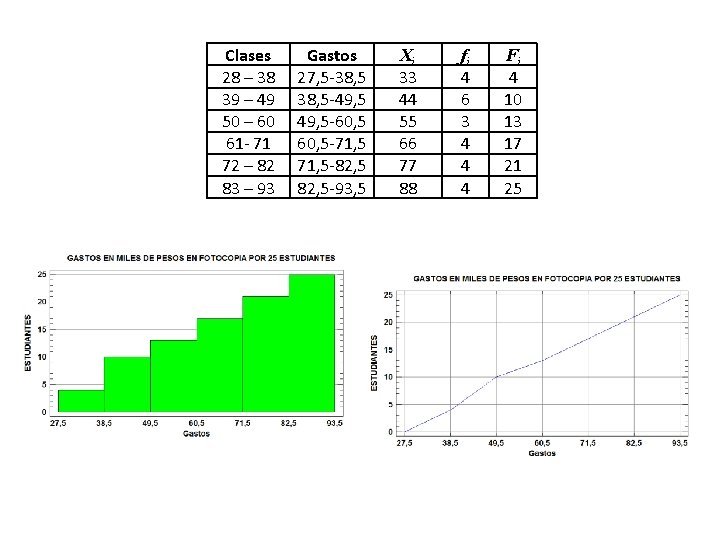
Clases 28 – 38 39 – 49 50 – 60 61 - 71 72 – 82 83 – 93 Gastos 27, 5 -38, 5 -49, 5 -60, 5 -71, 5 -82, 5 -93, 5 Xi 33 44 55 66 77 88 fi 4 6 3 4 4 4 Fi 4 10 13 17 21 25

11. Los datos adjuntos representan una muestra del aumento de precios (en pesos) de la gasolina extra en una cierta ciudad a lo largo de un año en particular. 123, 9 121, 9 126, 9 120, 8 115, 9 127, 9 126, 9 119, 9 115, 9 121, 9 130, 9 122, 8 118, 9 117, 9 129, 9 121, 9 126, 9 119, 8 131, 9 122, 8 132, 9 137, 9 116, 9 115, 9 119, 9 Mediante cinco clases construya una tabla de frecuencias relativas acumuladas agrupadas. Solución

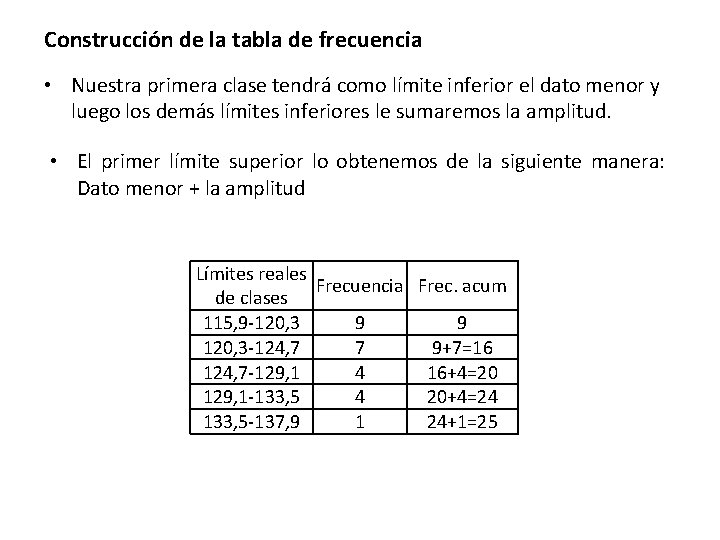
Construcción de la tabla de frecuencia • Nuestra primera clase tendrá como límite inferior el dato menor y luego los demás límites inferiores le sumaremos la amplitud. • El primer límite superior lo obtenemos de la siguiente manera: Dato menor + la amplitud Límites reales Frecuencia Frec. acum de clases 115, 9 -120, 3 9 9 120, 3 -124, 7 7 9+7=16 124, 7 -129, 1 4 16+4=20 129, 1 -133, 5 4 20+4=24 133, 5 -137, 9 1 24+1=25

Solución utilizando la regla de Sturges Construcción de la tabla de frecuencia • Nuestra primera clase tendrá como límite inferior el dato menor y luego los demás límites inferiores le sumaremos la amplitud. • El primer límite superior lo obtenemos de la siguiente manera: Dato menor + la amplitud – 0, 1 Clases 115, 9 -119, 5 119, 6 -123, 2 123, 3 -126, 9 127, 0 -130, 6 130, 7 -134, 3 134, 4 -138, 0 Limites reales 115, 85 -119, 55 -123, 25 -126, 95 -130, 65 -134, 35 -138, 05 Frecuencia Frec. Acum. 6 6 9 15 4 19 2 21 3 24 1 25

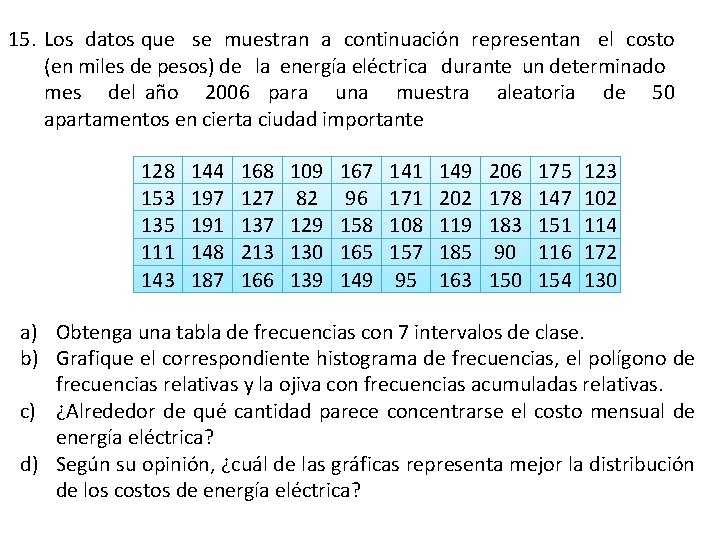
15. Los datos que se muestran a continuación representan el costo (en miles de pesos) de la energía eléctrica durante un determinado mes del año 2006 para una muestra aleatoria de 50 apartamentos en cierta ciudad importante 128 153 135 111 143 144 197 191 148 187 168 127 137 213 166 109 82 129 130 139 167 96 158 165 149 141 171 108 157 95 149 202 119 185 163 206 178 183 90 150 175 147 151 116 154 123 102 114 172 130 a) Obtenga una tabla de frecuencias con 7 intervalos de clase. b) Grafique el correspondiente histograma de frecuencias, el polígono de frecuencias relativas y la ojiva con frecuencias acumuladas relativas. c) ¿Alrededor de qué cantidad parece concentrarse el costo mensual de energía eléctrica? d) Según su opinión, ¿cuál de las gráficas representa mejor la distribución de los costos de energía eléctrica?

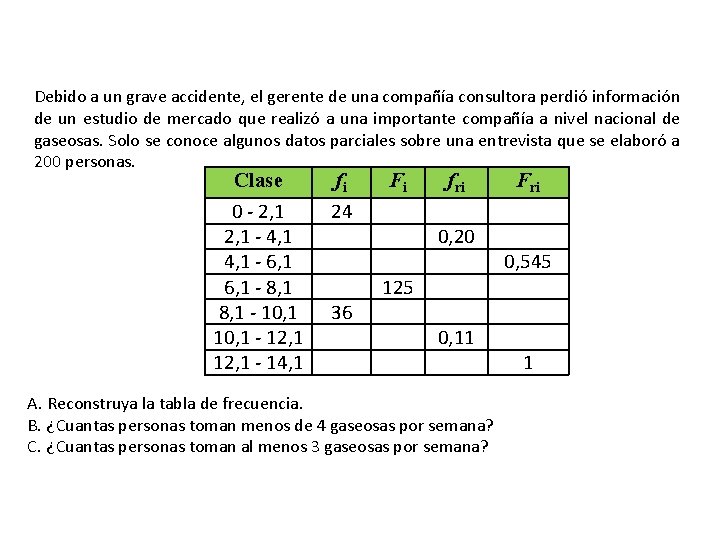
Debido a un grave accidente, el gerente de una compañía consultora perdió información de un estudio de mercado que realizó a una importante compañía a nivel nacional de gaseosas. Solo se conoce algunos datos parciales sobre una entrevista que se elaboró a 200 personas. Clase 0 - 2, 1 - 4, 1 - 6, 1 - 8, 1 - 10, 1 - 12, 1 - 14, 1 fi 24 36 Fi fri 0, 20 125 0, 11 A. Reconstruya la tabla de frecuencia. B. ¿Cuantas personas toman menos de 4 gaseosas por semana? C. ¿Cuantas personas toman al menos 3 gaseosas por semana? Fri 0, 545 1

1. 3 Análisis de datos en tablas de frecuencias no agrupadas Medidas de tendencia central o de centralización La estadística busca entre otras cosas, describir las características típicas de conjuntos de datos. Las medidas de tendencia central corresponden a valores que generalmente se ubican en la parte central de un conjunto de datos que nos ayudan a resumir la información en un sólo número.

Moda La moda, si se da, es el dato con mayor frecuencia. Medidas de colocación o de posición relativa Una medida de colocación o de posición relativa para una distribución de frecuencias es aquel valor para el cual una porción específica de la distribución queda en o debajo de él. La mediana, los percentiles, deciles y cuartiles son ejemplos de medidas de posición relativa.

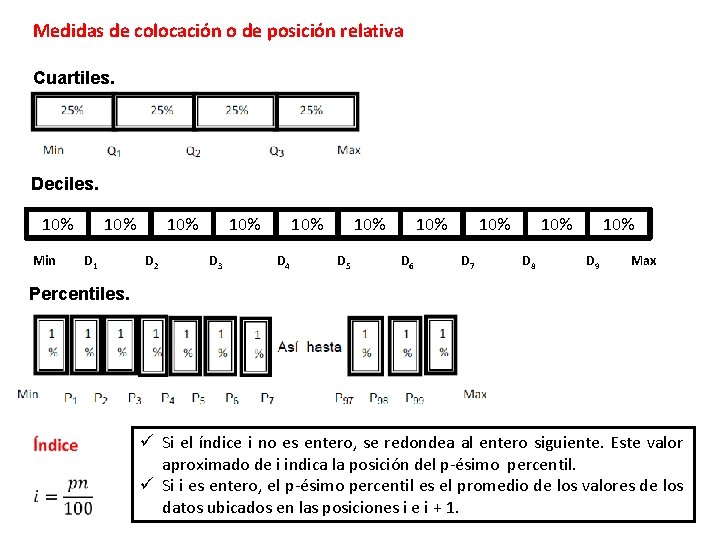
Medidas de colocación o de posición relativa Cuartiles. Deciles. 10% Min 10% D 1 10% D 2 10% D 3 10% D 4 10% D 5 10% D 6 10% D 7 10% D 8 10% D 9 Max Percentiles. ü Si el índice i no es entero, se redondea al entero siguiente. Este valor aproximado de i indica la posición del p-ésimo percentil. ü Si i es entero, el p-ésimo percentil es el promedio de los valores de los datos ubicados en las posiciones i e i + 1.

Medidas de dispersión o de variabilidad Las medidas de dispersión nos informan sobre cuánto se alejan del centro los valores de la distribución. Una medida de centralización, casi nunca es suficiente por sí sola, para analizar adecuadamente las características de un conjunto de datos. Por lo general, necesitaremos, además, una medida de la dispersión o variación de los datos, entre las que analizaremos se encuentran el rango o recorrido, el rango intercuartil, la desviación, la varianza y la desviación estándar.

EJERCICIOS 45. La tabla siguiente contiene los salarios (en miles de pesos) de 30 trabajadores. Salario anual 550 Frecuencia 8 600 6 700 7 800 5 3. 000 4 (a)Determine la moda, la mediana y el rango medio (b)¿Cuál medida de tendencia usaría para determinar el valor central? Explique. (c) ¿Cuál es el primer cuartil, el tercer cuartil y el sexto decil? (d) Encuentre el rango, la desviación estándar y el rango intercuartil.

PROCEDIMIENTOS UTILIZANDO LA CALCULADORA

Medidas de formas Las medidas de forma se clasifican en medidas de asimetría (o coeficiente de sesgo) y medidas de curtosis (o de apuntamiento). Simetría Decimos que una distribución de frecuencias es simétrica cuando lo es su representación gráfica, es decir, los datos equidistantes a una medida central de la misma tienen frecuencias iguales. Esta medida central coincide con la mediana y la media. Asimetría Una distribución de frecuencias que no es simétrica, se denomina asimétrica. La asimetría se puede presentar a la derecha ( asimetría positiva) o a la izquierda ( asimetría negativa) si la representación grafica está más “estirada” hacia la derecha o hacia la izquierda, respectivamente.

EJERCICIOS 49. La tabla siguiente da una muestra de los tiempos de recorrido (en minutos) de un camino de 2, 5 millas para el carro de Humberto y el de Greyci. Encuentre el promedio de los tiempos de recorrido para cada uno de los carros. (b) Calcule la varianza de los tiempos de recorrido para cada uno de los carros, respectivamente. (c) ¿Qué auto tuvo un desempeño más consistente, si la consistencia se mide con la varianza? (d) Encuentre el coeficiente de variación para cada carro y comente al respecto.

1. 4 Análisis de datos en tablas de frecuencias agrupadas Es posible calcular las medidas de tendencia central y dispersión para datos exhibidos en una tabla de frecuencia agrupada, pero sus valores no son exactos sino únicamente aproximados. Eso se debe al desconocimiento de las medidas en grupo, las cuales se han colocado en intervalos de clase. En esta sección, describiremos procedimientos para calcular medidas numéricas que resuman la información cuando sólo disponemos de datos agrupados.

DATOS AGRUPADOS 52. Se toma una muestra de 20 estudiantes. La tabla siguiente muestra la cantidad de tiempo (en horas) empleado por cada uno de estos estudiantes de dicha muestra en preparar un examen. Tiempo de estudio (Horas) Número de estudiantes 0– 3 2 3– 6 6 6– 9 7 9 – 12 4 12 - 15 1 (a) Hallar las frecuencias relativas y las frecuencias relativas acumuladas. (b) Estimar la media, la mediana, la moda y la desviación típica del tiempo de estudio.

53. Durante una epidemia de gripe, los tiempos de espera en cierto centro de salud fueron más largos de lo habitual. La siguiente tabla resume la distribución de los tiempos de espera para una muestra de 24 pacientes que visitaron el centro de salud durante este período. Tiempo de espera (horas) Número de pacientes 0– 1 7 1– 2 10 2– 3 5 3– 4 2 (a) Hallar las frecuencias acumuladas, relativas y relativas acumuladas. (b) Dibujar el histograma, un polígono y una ojiva. (c) Estimar la media, la mediana, la moda, la varianza y la desviación típica del tiempo de espera.