Optimization Techniques for Supply Network Models Simone Gttlich

Optimization Techniques for Supply Network Models Simone Göttlich Joint Work with: M. Herty, A. Klar (TU Kaiserslautern) 1. A. Fügenschuh, A. Martin (TU Darmstadt) 1. Workshop Math. Modelle in der Transport- und Produktionslogistik Bremen, 11. Januar 2008 11. 01. 2008 Simone Göttlich 07. 09. 2006

Motivation Simulation and Optimization of a Production Network Typical questions: 11. 01. 2008 n Investment costs and rentability n Topology of the network n Production mix and policy strategies Simone Göttlich

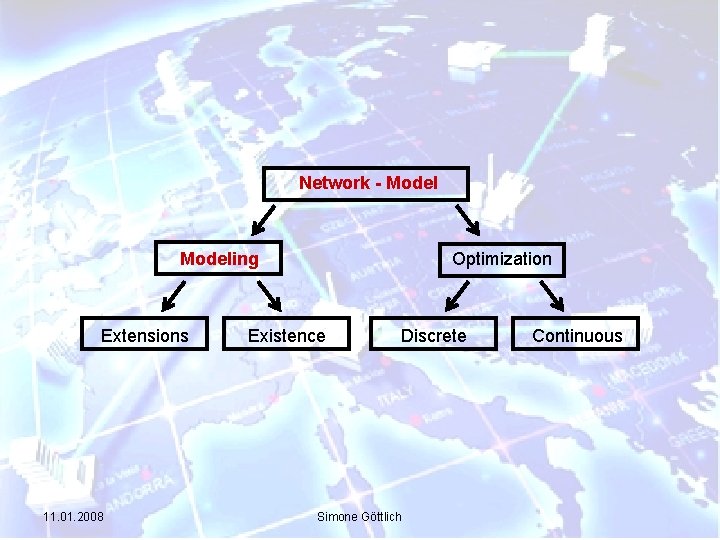
Network - Modeling Extensions 11. 01. 2008 Optimization Existence Discrete Simone Göttlich Continuous

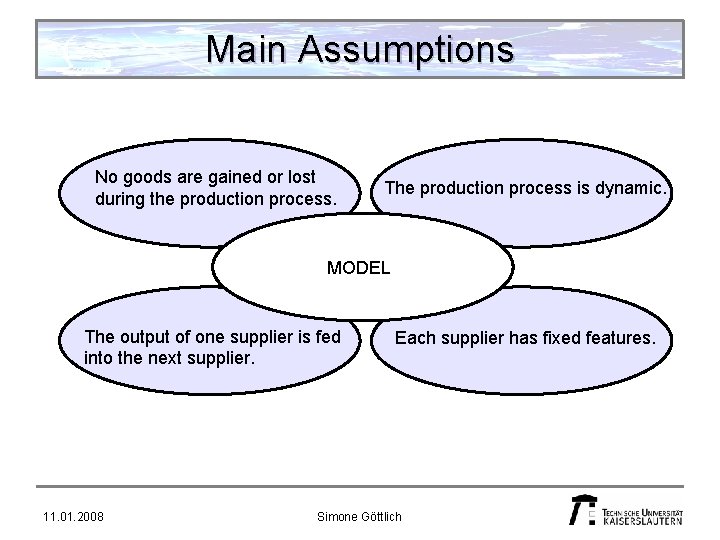
Main Assumptions No goods are gained or lost during the production process. The production process is dynamic. MODEL The output of one supplier is fed into the next supplier. 11. 01. 2008 Each supplier has fixed features. Simone Göttlich

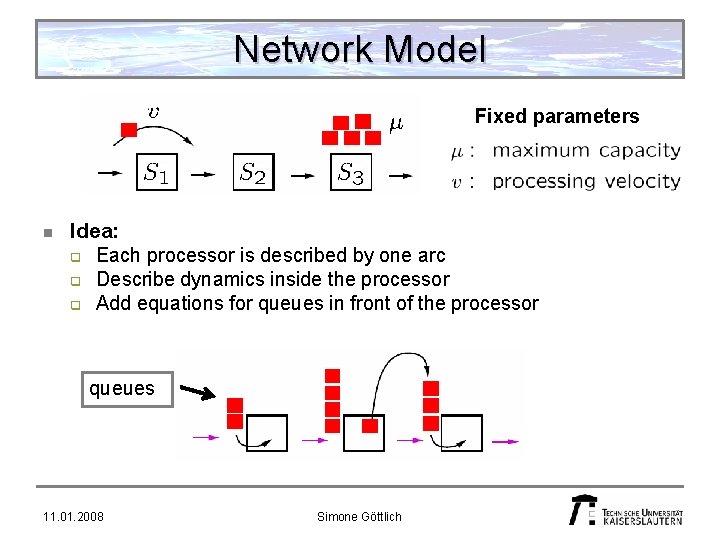
Network Model Fixed parameters n Idea: q Each processor is described by one arc q Describe dynamics inside the processor q Add equations for queues in front of the processor queues 11. 01. 2008 Simone Göttlich

Network Model See Göttlich, Herty, Klar (2005): Network models for supply chains Definition A production network is a finite directed graph (E, V) where each arc corresponds to a processor on the intervall Each processor has an associated queue in front. Processor: Queue: 11. 01. 2008 Simone Göttlich

Network Coupling Definition We define time-dependent distribution rates vertex with multiple outgoing arcs. The functions required to satisfy and Example: for each are Inflow into queue of arc 2 Inflow into queue of arc 3 will be obtained as solutions of the optimization problem 11. 01. 2008 Simone Göttlich

Network - Modeling Extensions 11. 01. 2008 Optimization Existence Discrete Simone Göttlich Continuous

Optimization Problem Controls Positive weights Cost functional Constraints Processor Queue Initial conditions 11. 01. 2008 Simone Göttlich

Solution Techniques Optimal control problem with PDE/ODE as constraints! How to solve ? Mixed Integer Programming (MIP) Adjoint Calculus MIP 11. 01. 2008 Simone Göttlich LP

Network - Modeling Extensions 11. 01. 2008 Optimization Existence Discrete Simone Göttlich Continuous

Mixed Integer Program (MIP) See Fügenschuh, Göttlich, Herty, Klar, Martin (2006): A Discrete Optimization Approach to Large Scale Networks based on PDEs A mixed-integer program is the minimization/maximization of a linear function subject to linear constraints. Problem: Modeling of the queue-outflow in a discete framework Solution: Reduce complexity (as less as possible binary variables) Relaxed queue-outflow 1 1 See Armbruster et al. (2006): Autonomous Control of Production Networks using a Pheromone Approach 11. 01. 2008 Simone Göttlich

Derivation MIP Problem: Suitable discretization of the -nonlinearity Idea: Introduce binary variables (decision variables) Outflow of the queue = Inflow to a processor Example: 11. 01. 2008 implies and Simone Göttlich

Mixed Integer Program Two-point Upwind discretization (PDE) and explicit Euler discretization (ODE) leads to maximize outflux processor queue outflow initial conditions 11. 01. 2008 Simone Göttlich

Advantage MIP Constraints can be easily added to the MIP model: § Bounded queues: n Optimal inflow profile: In other words: Find a maximum possible inflow to the network such that the queue-limits are not exceeded. 11. 01. 2008 Simone Göttlich

Disadvantage MIP The problem has n Goal q q q n binary variables! Reduce computational complexity Avoid rounding errors in the CPLEX solver Accelerate the solution procedure How to do that? q q Create a new preprocessing where PDE-knowledge is included Compute lower und upper bounds by bounds strengthening 11. 01. 2008 Simone Göttlich

Network - Modeling Extensions 11. 01. 2008 Optimization Existence Discrete Simone Göttlich Continuous

Adjoint Calculus See Göttlich, Herty, Kirchner, Klar (2006): Optimal Control for Continuous Supply Network Models Adjoint calculus is used to solve PDE and ODE constrained optimization problems. Following steps have to be performed: 1. Define the Lagrange – functional: Cost functional PDE processor ODE queue with Lagrange multipliers 11. 01. 2008 and Simone Göttlich

Adjoint Calculus 2. Derive the first order optimality system (KKT-system): Forward (state) equations: Backward (adjoint) equations: Gradient equation: 11. 01. 2008 Simone Göttlich

Network - Modeling Extensions 11. 01. 2008 Optimization Existence Discrete Simone Göttlich Continuous

Linear Program (LP) Idea: Use adjoint equations to prove the reformulation of the MIP as a LP MI Outflow of the queue P LP Remove the complementarity condition! Remark: The remaining equations remain unchanged! 11. 01. 2008 Simone Göttlich

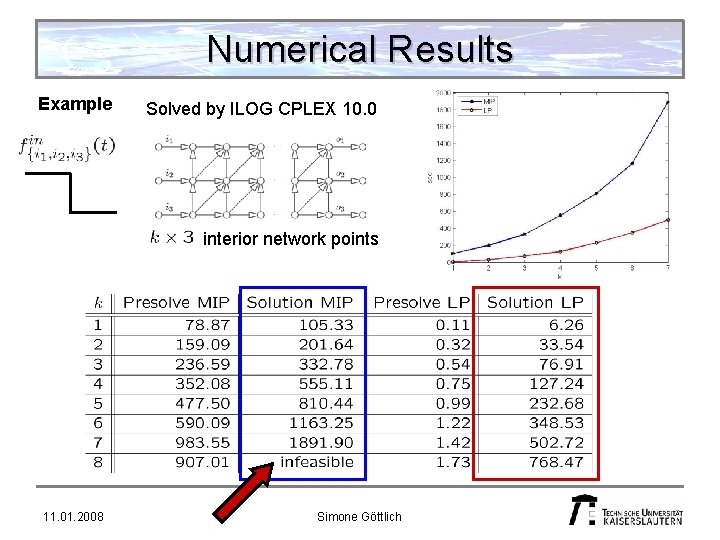
Numerical Results Example Solved by ILOG CPLEX 10. 0 interior network points 11. 01. 2008 Simone Göttlich

11. 01. 2008 Simone Göttlich